煤矿斜井管片衬砌与可压缩层联合支护的效果
2018-07-12肖明清
齐 春, 何 川, 封 坤, 肖明清
(1. 西南交通大学交通隧道工程教育部重点实验室, 四川 成都 610031; 2. 西南交通大学交通土木工程学院, 四川 成都 610031; 3.中铁二院工程集团有限责任公司, 四川 成都 610031; 4. 中铁第四勘察设计院集团有限公司, 湖北 武汉 430063)
随着煤矿开采深度的逐年加深,为满足矿井建设对“快速成井,安全可靠,综合费用低”等方面的高要求,采用盾构法修建煤矿井巷日益成为一种有效的选择方案.国内神华新街台格庙矿区、神东补连塔矿区目前已开展盾构法修建煤矿长距离斜井的探索.采用盾构法修建煤矿长距离斜井是今后建设高产高效煤矿斜井的发展方向[1-2].
随着斜井埋深的不断增加,高地应力问题不可避免.与浅埋隧道不同,高地应力背景下的深埋斜井开挖后主要承受围岩挤压型大变形产生的形变压力,其主要特点是变形持续时间长且具有重复性,支护完成后变形仍将持续[3].针对隧道大变形问题,长期以来国内外普遍采用加强型常规支护来应对,企图通过增加支护刚度以达到抑制围岩变形的目的[4],支护参数往往突破现有规范的推荐值,但由于围岩形变和荷载持续增加,支护往往难以抵抗不断增加的形变压力而破坏.因此,国内外学者提出了让压支护的理念,其主要思想是隧道(洞)或井巷开挖后,允许围岩发生一定的初期变形实现让压,从而实现围岩应力的部分释放,减小作用在支护结构上的形变压力[5-7].
对于采用盾构掘进和管片衬砌支护的深部斜井,借鉴传统矿山法隧道的让压支护思想,提出在围岩与管片间的空隙吹填具有一定流动性和可压缩性的豆粒石(碎石)“可压缩层”的让压支护型式,以减缓围岩形变荷载向衬砌结构的传递.“可压缩层”是一种“边支边让,先柔后刚”的支护措施,它在支护过程中可发挥一定量值的支护力,又同时会随围岩收敛而产生压缩变形,吸收围岩压力,减小作用在管片衬砌上的围岩荷载.
目前,碎石作为一种性能良好的建筑材料在土木工程领域得到了广泛的应用,国内外学者也开展了大量研究.Swk等[8]研究了级配碎石的非线性特性,得出了级配碎石的非线性方程及回归参数;Werkmeister[9]和Brown[10]等通过室内动三轴试验研究了级配碎石的永久变形行为规律,认为永久变形随着荷载作用次数的增加而无限积累.田建勃等[11]研究了不同厚度碎石垫层的强度和变形特性,提出了一种测定碎石类土侧压力系数、泊松比和变形模量的试验方法.谷小阳[12]分析了级配碎石的力学非线性本构模型,并对级配碎石复合式基层沥青路面的力学性能进行了有限元分析,得到级配碎石层弹性模量和厚度对沥青路面性能指标的影响.
已有研究成果中,碎石层都是作为主要承载材料存在的.然而,当其作为管片壁后填充材料时,是否会对管片衬砌结构产生影响,以及作为碎石填充层主要性能指标的刚度、厚度等参数将会对管片衬砌的力学和变形性能产生何种影响等问题均尚未见报道.鉴于此,本文依托神华新街台格庙矿区主斜井工程开展研究,采用数值模拟手段研究可压缩层主要性能指标对管片衬砌结构的影响,并开展相似模型试验进行验证,以期为采用盾构法修建深部巷道(斜井)的支护型式设计提供参考.
1 工程概况
神华新街台格庙矿区位于鄂尔多斯市伊金霍洛旗和乌审旗境内,其1号矿井的主、副斜井由浅至深依次穿越侏罗系中下统延安组(J1-2y),侏罗系中统直罗组(J2z)、安定组(J2a),白垩系下统志丹群(K1zh)和第四系(Q4)地层,围岩主要岩性为粗粒砂岩、含砾粗粒砂岩、中粒砂岩、细粒砂岩、泥岩和砂岩与泥岩互层、砂质泥岩.围岩分类以Ⅳ类、Ⅴ类为主.工程主斜井坡度为-6°,长度为6 553 m,最大埋深685 m.盾构掘进段长6 402.691 m.斜井开挖直径7.62 m,净空直径6.60 m,采用C40预制钢筋混凝土管片支护,管片衬砌厚350 mm,幅宽1 500 mm,采用左右转弯环管片衬砌错缝拼装.管片分块如图1所示,图中,ZF、ZL1、ZL2、ZB1~ZB4均为管片分块编号.

图1 管片分块示意Fig.1 Schematic of segment division
2 数值计算
2.1 计算模型
根据参考文献[13-14],分别建立梁-弹簧模型和考虑刚度折减的匀质圆环模型,利用管片衬砌最大变形等效得到匀质圆环模型的刚度有效系数η=0.62.在此基础上,采用ABAQUS软件建立围岩、可压缩层和管片衬砌相互作用的地层-结构模型.围岩和可压缩层分别采用平面应变减缩积分单元(CPE4R)和平面应变非协调模式单元(CPE4I)模拟,管片衬砌采用二维线性梁单元(B21)模拟.衬砌和可压缩层之间建立面-面接触(surface to surface).围岩材料满足Mohr-Coulomb屈服准则,可压缩层和管片结构按弹性材料考虑.各材料的物理力学参数如表1所示.

表1 地层及结构物理力学参数Tab.1 Parameters of seepage property for sandstone
计算模型的各边界距洞室中心的距离为40 m(约5.5D,D为开挖直径).不考虑自重荷载及开挖过程,地层-可压缩层-管片衬砌系统所受外荷载通过在模型4个外边界施加法向均布压力实现.其中竖向压力折算土柱高度依次从10 m按照10 m的级差增加至100 m,水平压力根据竖向压力和侧压力系数计算得到,侧压力系数保持0.5不变.分析模型如图2所示.

图2 有限元分析模型示意Fig.2 Analysis model of FEM
计算工况包括有、无可压缩层两类,对于设置可压缩层的工况,其参数取值根据研究目的不同而有所不同,具体可见第2.2节.
2.2 结果分析
(1) 有无可压缩层的影响
对管片衬砌背后存在可压缩层和不存在可压缩层情况下结构所受围岩压力、弯矩、轴力和变形进行对比.对于存在可压缩层的情况,取Ec=0.1Eg(Ec、Eg分别为可压缩层和围岩的变形模量),厚度d=0.4 m;竖向土柱高度为100 m.
有无可压缩层时的计算结果分别如图3、表2所示.
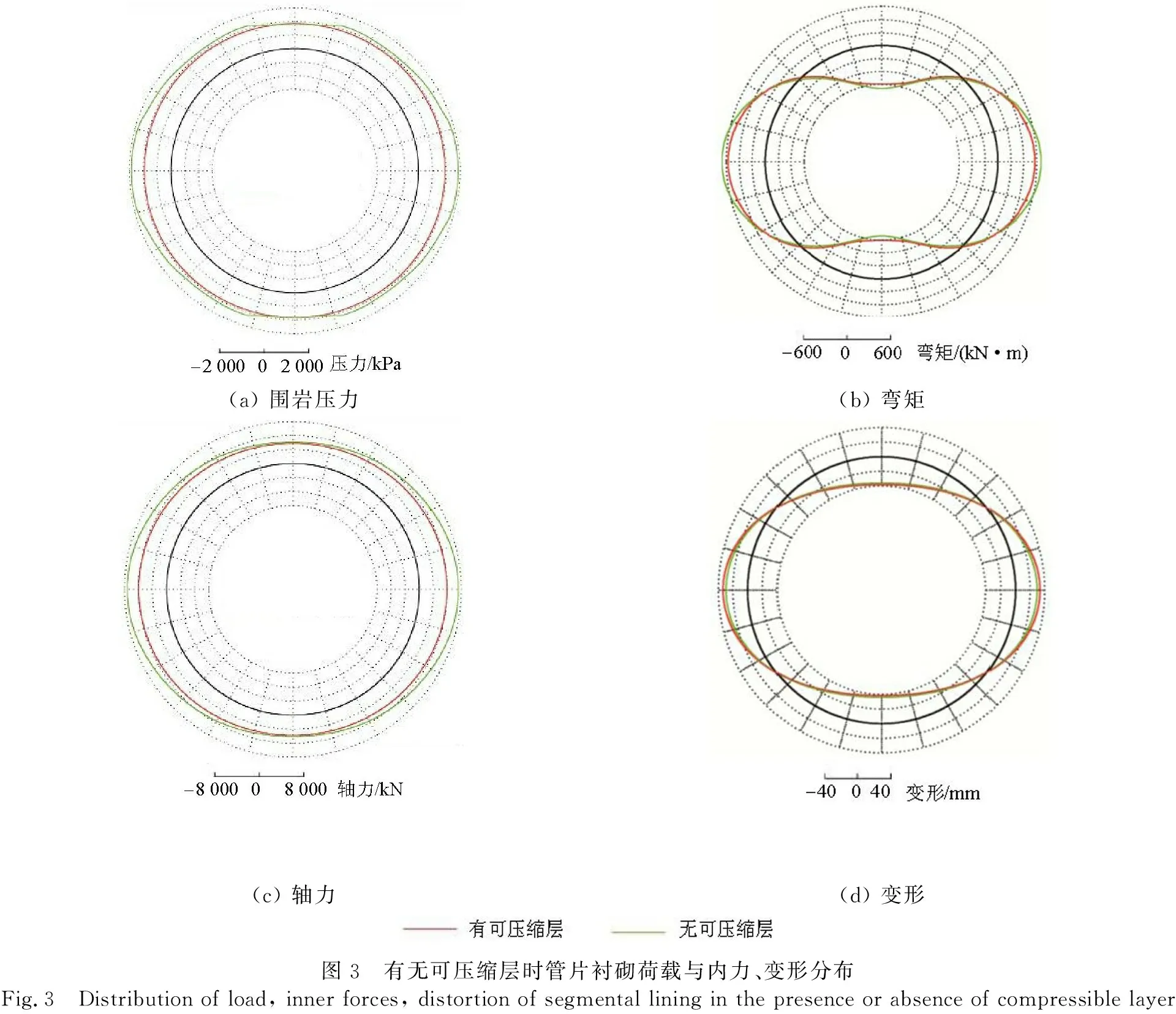
(a) 围岩压力(b) 弯矩(c) 轴力(d) 变形图3 有无可压缩层时管片衬砌荷载与内力、变形分布Fig.3 Distribution of load, inner forces, distortion of segmental lining in the presence or absence of compressible layer

表2 有无可压缩层时管片衬砌内力和变形对比Tab.2 Comparison of internal force and deformation of segment lining in the presence or absence of compressible layer
可压缩层对管片所受围岩压力的分布和量值均有较大影响.当管片壁后没有可压缩层时,围岩传递至管片上的压力呈现水平方向大、竖直方向小的不均匀分布特点,其最大和最小值分别位于拱腰和拱顶,这与文献[15]采用解析法得到的规律是类似的.围岩压力的最大和最小值分别为1 912、1 216 kPa.当管片壁后设置可压缩层后,能够吸收一部分围岩压力起到让压效果,并能够将围岩压力更均匀的传递到管片上.从图3中可以看出,可压缩层的存在大大减小了最大和最小围岩压力的差值,其量值分别为1 278 kPa和1 227 kPa,管片结构处于均匀受压状态,这对结构受力是有利的.
可压缩层对管片弯矩和轴力的最值有一定影响,但对其分布的影响不大.不存在可压缩层时,最大正负弯矩分别为624 kN·m和-656 kN·m;存在可压缩层时,最大正负弯矩分别减小至564 kN·m和-566 kN·m,减幅分别为9.6%和13.4%.可压缩层对管片轴力的影响与弯矩类似,可压缩层使管片最大和最小轴力分别减小了28.8%和5.4%.
可压缩层的存在对管片变形基本没有影响.
(2) 可压缩层刚度的影响
保持可压缩层厚度d=0.4 m,取其Ec=0.1Eg~10.0Eg,研究不同可压缩层刚度下管片所受围岩压力和内力、变形的变化情况.不同工况条件下的计算结果如图4、表3所示.由于可压缩层刚度变化时围岩压力沿环向有增有减,考虑到围岩压力均匀分布有利于管片结构受力,因此表3中定义围岩压力的相对极差RP为管片衬砌所受围岩压力最大值和最小值之差与平均值之比,以反映围岩压力的均匀性.

(a) 围岩压力(b) 弯矩(c) 轴力(d) 变形图4 不同可压缩层刚度时管片衬砌荷载与内力、变形环向分布Fig.4 Distribution of load, inner forces, distortion of segmental lining with different compressible layer stiffness

表3 不同可压缩层刚度时管片衬砌内力和变形对比Tab.3 Comparison of internal force and deformation of segment lining with different compressible layer stiffness
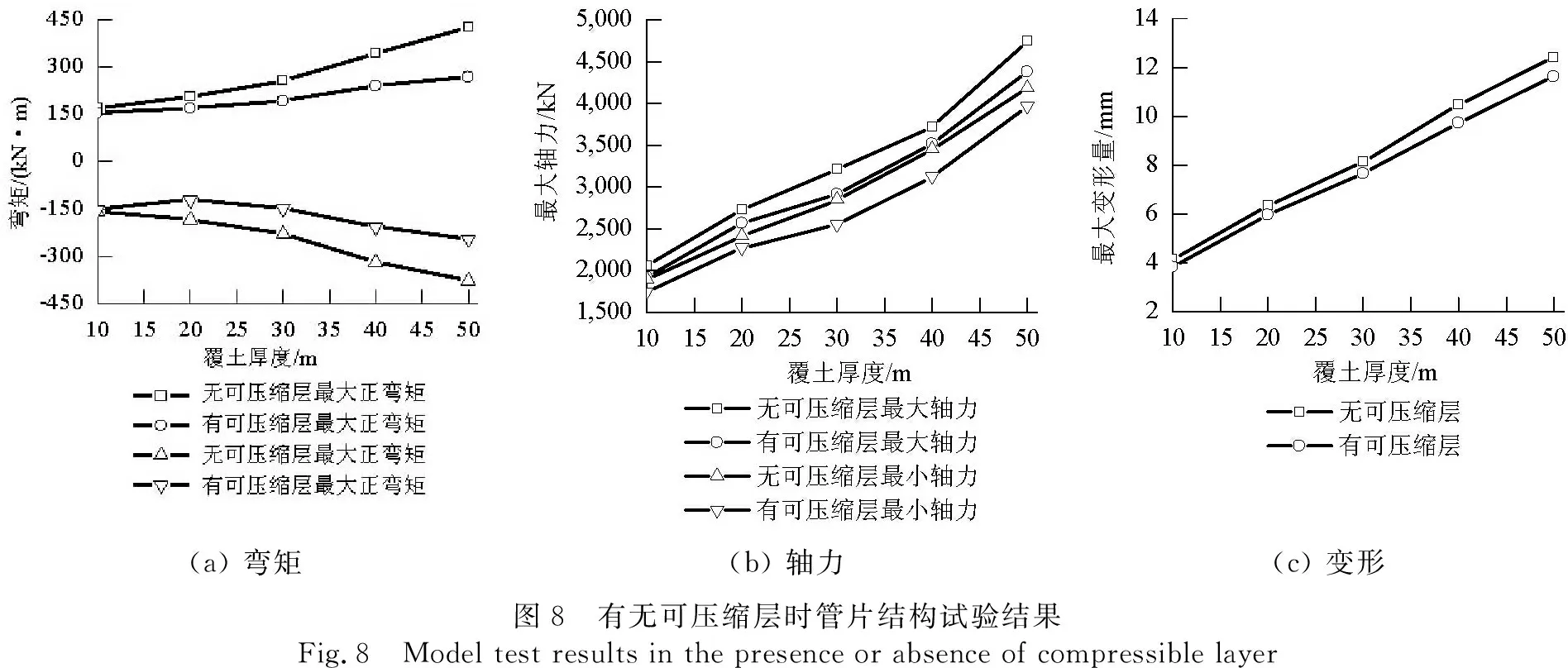
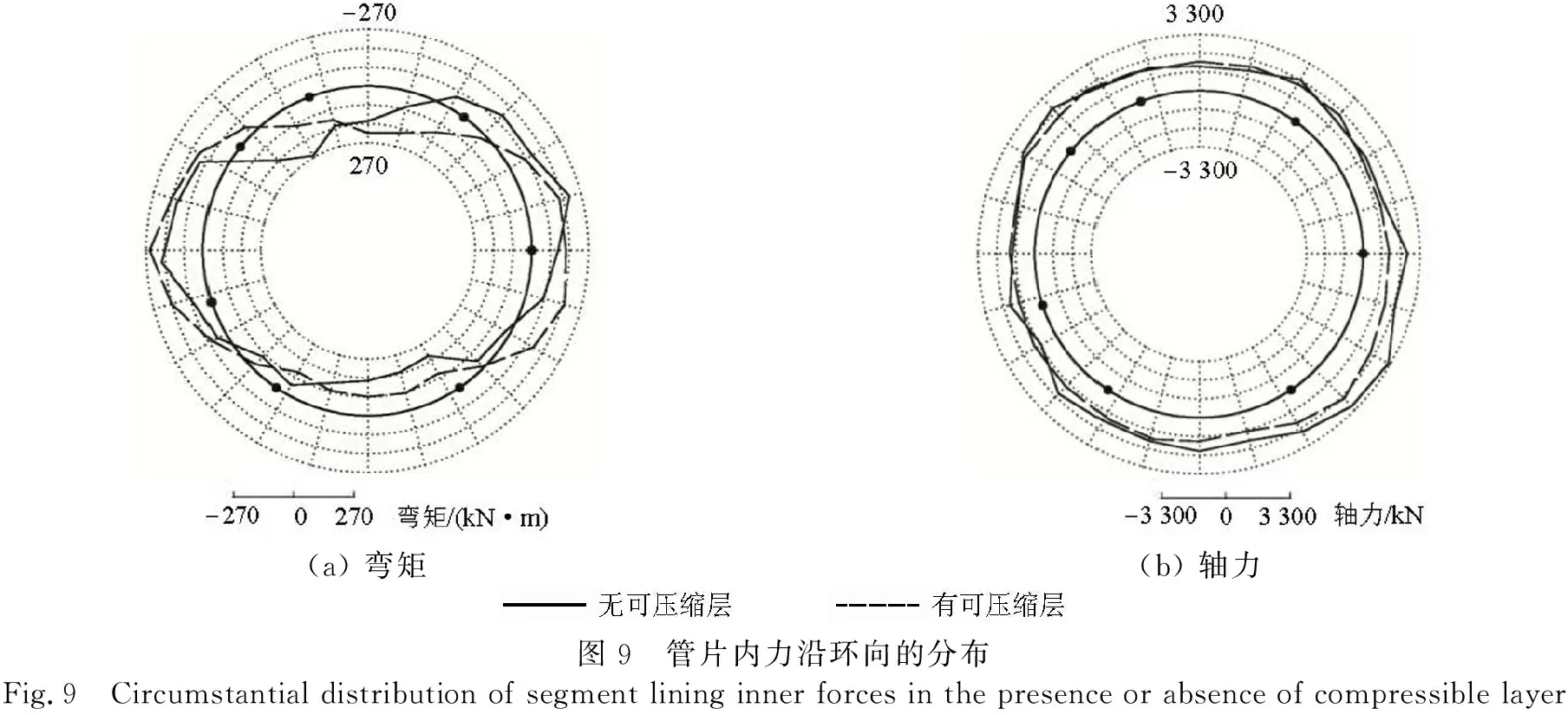
当d一定时:① 管片所受围岩压力的分布和量值均随着Ec的增大而变化.当Ec (3) 可压缩层厚度的影响 保持Ec=0.1Eg,分别取其厚度d=0.2,0.4,0.6,0.8 m和1.0 m,研究不同可压缩层厚度下管片所受围岩压力和内力、变形的变化情况. 不同工况条件下的计算结果如图5、表4所示. (a) 围岩压力(b) 弯矩(c) 轴力(d) 变形图5 不同可压缩层厚度时管片衬砌荷载与内力、变形分布Fig.5 Distribution of load, inner forces, distortion of segmental lining with different compressible layer thickness 表4 不同可压缩层厚度时管片衬砌内力和变形对比Tab.4 Comparison of internal force and deformation of segment lining with different compressible layer thickness 当Ec一定时: ① 管片所受围岩压力的分布和量值均随着d的增大而变化.随着d的增大,可压缩层对围岩压力吸收和重分布的效果越发显著,使得传递到管片上的围岩压力分布趋于均匀.不同厚度时,Rp=12.2%,4.2%,0.5%,2.2%,3.8%.总体而言,在可压缩层刚度一定的条件下,适度增大其厚度可使传递至管片衬砌上的围岩压力更为均匀,但超过此厚度后可压缩层厚度的继续增大会使围岩压力均匀性降低. 对于本文研究工况,当可压缩层厚度与管片厚度之比,即0.60/0.35=1.7时,可使传递到管片衬砌上的围岩压力最小. ② 可压缩层厚度的变化对管片弯矩基本没有影响,但对管片轴力的量值有影响. 以最大轴力为例,当d从0.2 m增加到1.0 m时,其量减小了26.2%.虽然在研究所涉及的厚度范围内,随着d的增大管片最大轴力持续减小,但减幅逐渐减小.可以推断,在一定范围内增大d将会降低管片轴力,超出这个范围后对管片轴力的影响较小. ③ 可压缩层厚度的变化对管片变形基本没有影响. 试验以依托工程穿越的典型地层为原型,以几何相似比1/20和容重相似比1/1为基础相似比,采用特定比例的重晶石粉、石英砂、松香和凡士林的混合物配制围岩材料,如表5所示.管片衬砌采用水∶石膏∶硅藻土=1.5∶1.0∶0.1 预制加工而成,主筋通过刚度等效原理采用铁丝网模拟;管片环向接头通过开槽的方式模拟,开槽深度通过计算确定,如表6所示;管片环间接头通过一定直径的钢棒模拟[16].对于管片壁后的可压缩层,考虑到其主要作用是通过散粒体材料的流动转移导致的孔隙率减小来实现让压[17],而材料本身的变形可以忽略,因此,本试验采用较小粒径的碎石模拟可压缩层材料,如图6所示. 试验采用“盾构隧道-地层复合体模型试验系统”开展,装置总体尺寸为3.00 m(长)×3.00 m(宽)×0.16 m(高),如图7所示. 该试验系统采用卧式加载方式,可实现竖向(Ⅰ方向)、水平(Ⅱ方向)和纵向(Ⅲ方向)的荷载施加.每个方向均由4台液压千斤顶通过工字钢或盖板作为荷载分配梁对土体施加均布面荷载.其中Ⅰ、Ⅱ方向的千斤顶两两成组,对称布置.Ⅰ方向施加荷载为结构所受竖向荷载,根据地层条件和埋深等因素计算确定;Ⅱ方向施加水平荷载,根据侧压力系数和I方向荷载计算确定.Ⅲ方向为纵向荷载,通过盖板施加,目的是保证加载过程满足平面应变状态[18]. 表5 材料物理力学参数Tab.5 Mechanical parameters of materials 表6 环向接头对应槽缝深度Tab.6 Cutting depth of groove for circumferential joints 图6 可压缩层设置Fig.6 Installation of compressible layer 图7 盾构隧道-地层复合体模型试验系统Fig.7 Equipment of model tests 试验的主要目的是探究管片壁后设置可压缩层是否对管片受力和变形产生影响,因此设置2组工况:管片衬砌和管片衬砌+可压缩层(厚0.6 m). 加载过程保持侧压力系数0.5不变,竖向土压力从0按照10 m等效覆土厚度的增量逐级加载.每级荷载保持约10 min,待数据稳定后进行下一级加载.水平土压力由竖向土压力和侧压力系数得到. 有无可压缩层条件下管片衬砌弯矩、轴力和变形随土压的变化情况如图8所示.图中数据为将试验数据按相似关系换算至原型结构后的结果,横坐标为相应土压对应的覆土厚度,下同. (a) 弯矩(b) 轴力(c) 变形图8 有无可压缩层时管片结构试验结果Fig.8 Model test results in the presence or absence of compressible layer 从图8可以看出:(1) 当无可压缩层时,随着土压增大,管片衬砌结构弯矩不断增大,且增长变化曲线存在明显的拐点,位于30 m土柱位置;当土压从10 m增加到30 m,最大正弯矩从171.36 kN·m增大到257.25 kN·m,增幅50.1%;当土压继续从30 m 增加到50 m,最大正弯矩从257.25 kN·m增大到427.18 kN·m,增幅66.1%. (2) 管片轴力也随土压的增大而增大,且最大、最小轴力量值较为均匀,增幅也很接近.当土压从 10 m增加至50 m时,最大轴力从2 064.58 kN增加至4 744.44 kN,增幅130%,最小轴力从1 924.19 kN增加至4374.38 kN,增幅127%. (3) 管片结构最大变形量随着土压的增大近似线性增大.当土压从10 m增加至50 m时,最大变形量从4.13 mm增加至12.39 mm. 当管片壁后设置碎石可压缩层,与管片组成联合支护体系时,管片弯矩仍随着土压的增大而增大,但增幅小于不设置可压缩层时.从图8可以看出,可压缩层的存在使得最大弯矩的增长更为平稳和缓慢.相同土压条件下,存在可压缩层时管片衬砌的最大和最小弯矩均小于无可压缩层时的值,且土压越大,有无可压缩层时管片弯矩的差异越明显,说明当管片壁后存在可压缩层时,对于较高的土压水平,可压缩层能够通过自身的挤密吸收一部分土压力,减小传递至管片上的荷载,使管片荷载的增大过程更为平稳,从而得到更小且分布更均匀的弯矩. 对于管片轴力,存在可压缩层情况下轴力量值也随土压的增大而增大,但同级土压条件下,轴力量值较无可压缩层时的要小.管片结构最大变形量随着土压的增大近似线性增大.当土压从10 m增加至50 m时,最大变形量从6.03 mm增加至11.77 mm.与无可压缩层时的差别不大. 以30 m覆土厚度为例,有无可压缩层条件下管片弯矩和轴力沿环向的分布情况如图9所示.从图9可以看出:无可压缩层时,管片最大正弯矩257.25 kN·m,位于左侧拱肩附近,最大负弯矩-227.96 kN·m,位于右侧拱腰附近;有可压缩层时,最大正负弯矩分别为206.06、-199.47 kN·m,分别位于拱顶和右侧拱腰附近.相比无可压缩层,管片最大正负弯矩分别减小了19.9%和12.5%;可压缩层的存在不仅降低了弯矩的量值,还使得弯矩沿环向的分布更为均匀. 无可压缩层时,管片最大轴力 3 212.79 kN,位于右侧拱脚附近;有可压缩层情况下,最大轴力2 756.57 kN,仍位于右侧拱脚附近.相比无可压缩层,管片最大轴力减小了14.2%.可压缩层不仅降低了轴力的量值,还使得轴力沿环向的分布更均匀. 试验过程中还发现,可压缩层的存在提高了管片的极限承载力.不存在可压缩层时,当土压由50 m 继续增大时,管片内力和变形均急剧增大,此时管片环出现明显的椭变,管片右拱腰位置内壁发现可见裂缝,如图10所示. (a) 弯矩(b) 轴力图9 管片内力沿环向的分布Fig.9 Circumstantial distribution of segment lining inner forces in the presence or absence of compressible layer (a) 右拱腰裂缝 (b) 左拱腰裂缝图10 无可压缩层时管片裂缝情况Fig.10 Crack distribution in the absence of compressible layer 当土压继续增大,椭变更加明显,裂缝长度和宽度均不断扩展,左侧拱腰也产生裂缝.当土压增至70 m时,管片右拱腰处断裂,管片环失稳.存在可压缩层时,当土压持续增大,未发现管片内力和变形急剧增大的现象.当土压增至70 m时,管片出现椭变.随着土压继续增大,椭变更加明显.由于土体中央部分纵向约束不足,此时由于土压已经处于很高的水平,可压缩层压缩至极限,逐渐从下方涌入衬砌环内部,管片仰拱块承受极高土压,且由于其刚度较大,无法通过变形释放荷载,最终产生表面剥落并断裂,结构破坏,此时土压为90 m(图11). 图11 有可压缩层时管片环破坏形态Fig.11 Failure mode in the presence of compressible layer (1) 管片壁后设置可压缩层可吸收一部分围岩压力,起到让压效果,并能够将围岩压力更均匀的传递到管片上.可压缩层的存在会对管片轴力的量值产生影响,在局部范围内对弯矩产生影响,而对管片变形影响甚微.(2) 随着可压缩层刚度的增大,管片承受较大且分布不均匀的围岩压力.弯矩在局部范围内有所减小,轴力有较大幅度的增大.当可压缩层相对围岩“较软”时,以上各影响更明显,对管片变形的影响则很小.(3) 随着可压缩层厚度的增大,传递到管片上的围岩压力分布越均匀.弯矩在局部范围内有所增大,轴力则持续减小,但减小速度逐渐下降.超出一定厚度后,影响逐渐减弱.可压缩层刚度的变化对管片变形基本没影响.(4) 管片壁后可压缩层的存在使管片结构弯矩和轴力的增长更平缓,量值也更小,且土压越大差异越明显.说明可压缩层能够通过自身的挤密吸收部分土压力且促使应力重分布,减小并均匀化传递至管片上的荷载.(5) 可压缩层的存在能提高管片的极限承载力.无可压缩层时,当土压大于50 m时,管片环出现明显的椭变,右拱腰内壁出现可见裂缝;土压增至70 m时,管片右拱腰处断裂,管片环失稳.存在可压缩层时,土压增至70 m时管片才出现明显椭变,当土压增至90 m时仰拱剥落断裂,结构破坏.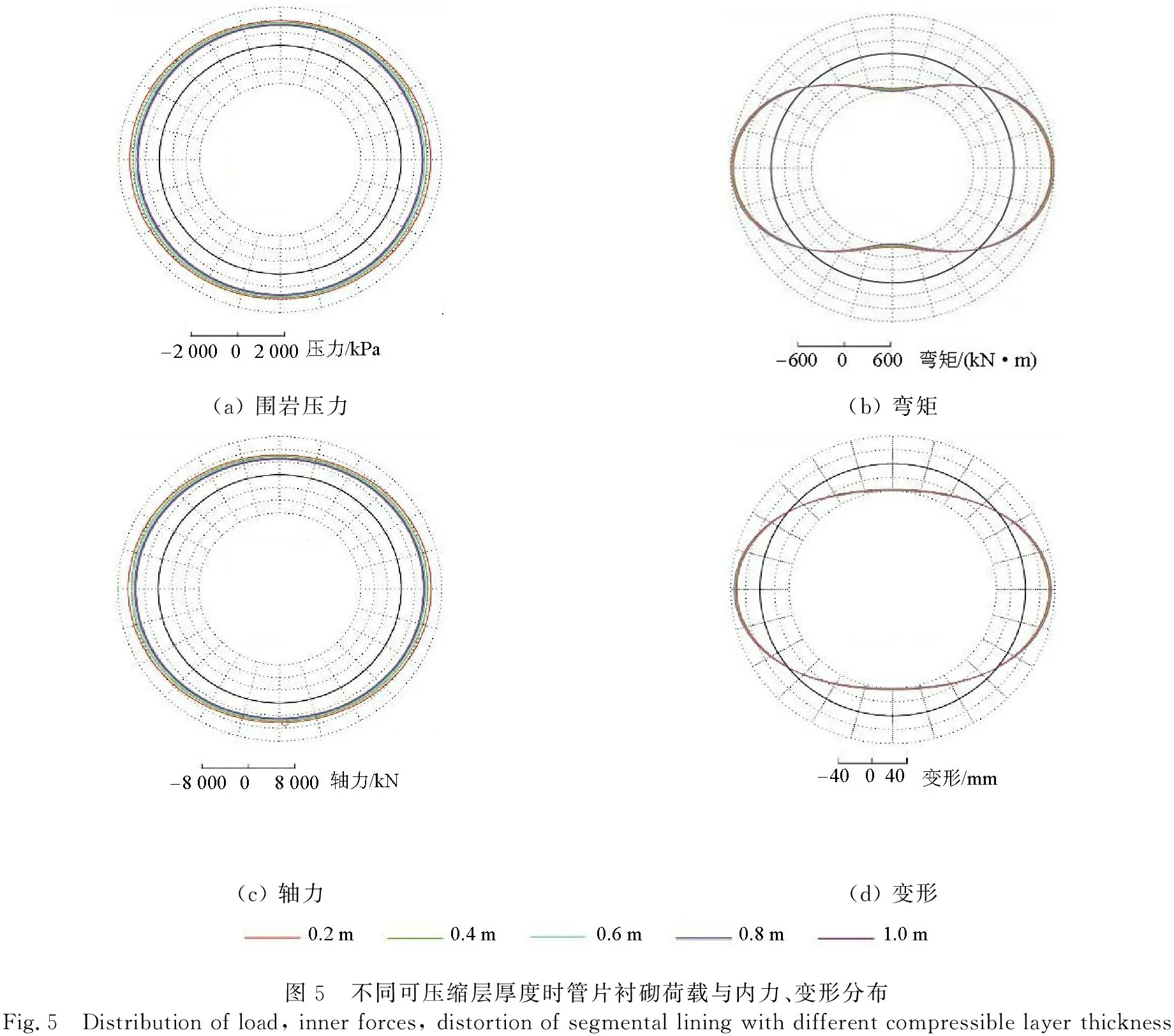
3 相似模型试验
3.1 模型试验概况




3.2 试验结果分析



4 结 论
