基于失效概率法的桥梁地震风险评估
2018-07-12崔圣爱崔恩旗
韩 兴, 崔圣爱, 崔恩旗, 苏 姣, 祝 兵
(西南交通大学土木工程学院, 四川 成都 610031)
我国地理位置特殊,国土面积辽阔,是全球大陆区域中最活跃的地震区之一.经过汶川地震和玉树地震的震害分析,桥梁受到地震破坏的影响很大,桥梁地震风险问题越来越受到工程技术人员关注.新建的南宁大桥、泰州长江大桥以及龙江大桥在对地震风险充分分析后进行了桥梁地震风险评估工作.总体来说,桥梁风险评估的意义是得出桥梁各个部分发生破坏导致整体结构失效的可能性.桥梁的地震风险概率可以通过定量和定性分析两种方式得到,定量分析需要大量的地震风险数据资料,而我国地震资料数据库并不完善;定性分析在我国地震风险评估中占据主导地位.
地震下桥梁风险概率可以用地震风险性(risk)来表达,是地震危险性(hazard)与易损性(fragility)的乘积.地震危险性是指地震风险分析的研究中风险事态发生的概率;结构易损性是指结构在风险事态作用下发生损伤或失效的概率.
国内外对于地震风险的评估方法不尽相同.国外从上世纪90年代开始对桥梁地震风险评估进行研究:Cornell[1]采用简化参数的方式将地震易损性函数带入了极限破坏概率表达式中得到了地震风险的解析表达式;Lupoi等[2]基于Cornell解析方法对混凝土桥梁进行了地震风险评估.后期学者研究[3]发现,虽然其评估精度基本满足工程需求,但仍然存在一定近似性.近些年来Kameshwar等[4]还进行了桥梁在地震和飓风两种灾害条件下的风险评估工作.国内学者于晓辉[5]基于云图法进行概率需求计算,获得相关参数,通过解析形式进行风险评估;阮欣等[6]对桥梁风险评估做了大量系统的研究,为了得出桥梁地震风险概率,采用的方法包括离散法和数值积分法;冯清海等[7]通过IDA(增量动力分析)的方法得到易损性曲线,采用蒙特卡洛抽样的方式,通过离散法求解风险概率,进行桥梁地震风险评估.但是对于铁路桥梁的风险评估工作较少,通过数值积分方法进行桥梁地震风险评估的文献也较少.
本文采用一种新的数值积分方法,通过地震加速度概率密度函数与桥梁结构易损性概率密度函数的数值积分,实现桥梁地震风险概率评估.具体来说,通过条带法进行桥梁抗震响应分析,得出桥梁在不同强度地震下的失效概率即易损性曲线;通过桥址处的抗震设计基本资料进行地震危险性分析;选取地震加速度作为求解积分方程的突破口,采用失效概率数值积分的方法得出桥梁的地震风险概率.该方法的优点有:(1) 条带法相对于云图法可以得出不同地震强度下桥梁响应的统计特性;(2) 数值积分方法充分利用所得到的桥梁易损性数据,并且可以考虑概率密度函数的连续性得到较为准确的结果.
本文详细推导了基于失效概率的地震风险评估方法,并以一座典型的高速铁路混凝土连续梁桥为算例,进行了地震风险概率计算.
1 桥梁地震风险评估
风险是在特定客观情况、特定时期内,某一事件的预期结果与实际结果间的偏离[8].风险评估的含义就是综合考虑统计事件发生的概率和造成后果的概率来进行事件对于原先体系的影响估计[9].对于桥梁地震风险评估而言,就是在考虑地震危险性的概率和结构破坏概率后,估计出地震对桥梁安全性的影响.根据概率论,可以得知风险函数为一种条件概率函数[5],如式(1).
P(F,H)=P(F|H)P(H),
(1)
式中:
P(F,H)为桥梁地震下破坏的风险概率;
P(H)为地震事件的发生概率;
P(F|H)为在某个地震事件情况下桥梁结构发生破坏的概率.
通过P(F|H)和P(H)的概率密度函数可以得到:

(2)
桥梁地震风险评估的主要工作集中在计算桥梁结构易损性和分析桥梁所处地址的地震危险性两个方面,其评估本质是为了得到桥梁地震下的失效概率.评估方法的实质就是桥梁结构易损性的概率密度函数和地震危险性的概率密度进行数值积分计算.
2 基于失效概率法的桥梁地震风险评估方法
2.1 桥梁结构易损性概率密度函数
易损性为在给定的地震参数(IM)下(如峰值地面加速度、谱加速度、地面运动的频谱特性或强震持续时间)结构构件或系统破坏超过某一个规定值的概率.结构的地震需求超过结构能力的失效概率为
(3)
式中:
Φ为标准正态分布累积密度函数;
μc为结构能力;
μd为需求值;


βc为结构能力的对数标准差;
βd为需求的对数标准差.
在混凝土连续梁桥中,选取墩底曲率和支座位移作为破坏指标,通过回归分析可以得出式(3)中所需系数.βd回归分析的具体内容可参见文献[10],易损性计算过程中没有考虑结构能力不确定性对于结构易损性的影响,βc在计算中取0.
选取合适的桥梁结构破坏模式与破坏指标之后,通过IDA的方法求解和绘制出桥梁结构的易损性曲线.
根据IDA的方法以及一阶可靠度理论可以得出桥梁结构系统易损性的概率曲线,即桥梁结构在不同地震情况下破坏程度的概率分布规律,也是桥梁破坏概率和地震峰值加速度的函数图形.根据文献[11],可以对易损性曲线进行简单的函数拟合.
f(F|a)=α+λ/(1+(a/δ)u),
(4)
式中:
α、λ、δ、u为函数拟合参数;
a为地震峰值加速度.
易损性曲线函数可以认为是与地震加速度有关的函数.即f(F|H)=f(F|a).如果可以探寻到f(H)也为加速度的函数,即如果f(H)=f(a)成立,就可以将式(2)写为

(5)
式(5)即为桥梁风险概率的数值积分公式,其积分变量为地震加速度,P(F,H)也就是桥梁地震风险概率.
2.2 地震危险性概率密度函数
地震危险性分析是求解桥梁地震风险概率的必要条件.地震危险性的基本含义在于桥址处受到地震损伤影响的可能性.我国桥梁设计中桥梁给出的仍是基于烈度的相关资料,与国际接轨的是地震动强度参数(地震加速度、幅值、持时等),需将地震烈度资料转化成风险评估需要的地震动峰值加速度.
地震烈度的概率函数符合式(6)的极值Ⅲ型分布[12].
(6)
式中:
i为烈度值;
ω为烈度最大值,一般地震烈度选用12度;
ε为众值烈度,即在规定时间内超越概率为0.632 的场地烈度;
K为形状参数.
根据以往工程经验,结合试验数据,将超越概率10%的烈度K值用来确定形状参数.
已知T为50年内地震烈度的极大值分布,为极值Ⅲ型,则在任意t年内的概率分布函数为
(7)
同时,刘恢先[13]给出了加速度与烈度的换算关系为
A=10ilg 2-0.01,
(8)
地震峰值加速度的概率可以通过极值Ⅱ型来描述.
(9)
式中:
ag为众值加速度,取一定时期内超越概率为0.632的峰值加速度;
所求得的加速度a单位为Gal(1g=1 000 Gal).
通过式(6)~(9)可以发现,根据桥址的地震烈度资料,可以推导出式(7)中的形状参数K,并且可以得出任意年限不同烈度地震的发生概率Fm(i).再通过式(8)可以得出所规定年限中不同烈度对应的峰值加速度值.得到一组峰值加速度与概率对应值之后,通过式(9)拟合出一定时期内众值加速度和形状参数K.
对式(7)进行求导得到峰值加速度概率密度函数为
(10)
ag与K都已经推导得出,f(a)也就是地震危险性的概率密度函数,即F(H)=f(a).
综合式(4)和(10),可以得到P(F,H),该函数为地震峰值加速度为变量的函数积分.在得到f(F|a)与f(a)的基础上可以通过数值积分的方式进行桥梁地震风险评估.
2.3 基于失效概率桥梁地震风险评估的一般步骤
综上所述可以得到桥梁地震风险评估的一般步骤:
步骤1建立桥梁的有限元模型,通过场地的资料选取若干条地震波进行计算.
步骤2通过IDA的方法对桥梁结构进行易损性分析,绘制易损性曲线.
步骤3根据式(4)给出的易损性曲线函数进行易损性概率函数拟合得到f(F|a).
步骤4通过桥址处抗震设防资料,采用式(7)确定桥梁结构在规定基准期内的烈度概率函数.
步骤5通过地震峰值加速度和地震烈度的关系,得出一组桥梁所在场地地震峰值加速度和发生概率的数值,经过函数拟合得出式(9)中的形状参数和规定期限内的众值加速度,经过求导得出式(10).
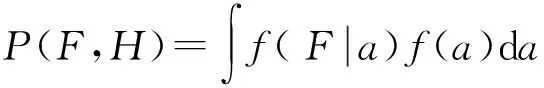
失效概率法的地震风险评估计算思路如图1所示.
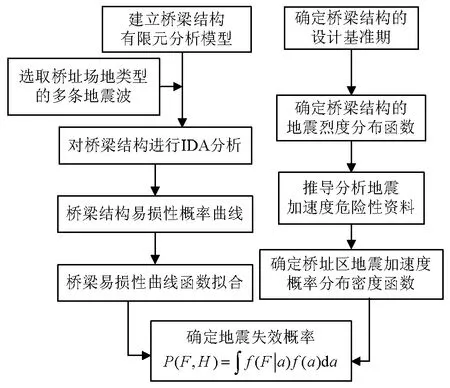
图1 地震风险评估流程Fig.1 Flow diagram of earthquake risk assessment
3 高速铁路连续梁桥的地震风险评估
3.1 工程概况及桥梁模型
研究对象为某高速铁路连续梁桥,桥跨径布置为32 m+48 m+32 m,如图2所示.主梁采用单箱单室箱形截面,中支点梁高为3.4 m,边支点及跨中梁高为2.8 m.全桥箱梁底板箱宽为4.5 m,桥面板宽为7.0 m,腹板厚为0.4~0.6 m,顶板厚为0.3 m.桥墩为圆端形截面.箱梁采用C50高性能混凝土,桥墩采用C35混凝土,承台采用C40混凝土.桥墩纵筋为HRB400,桩身受力钢筋及桥墩箍筋为HPB300.主梁与桥墩见图3.桥支座采用铁路连续梁球形支座,容许位移为150 mm.场地条件为一类,地震动反应谱特征周期为0.35 s.

图2 桥梁结构立面布置(单位:cm)Fig.2 Vertical layout of bridge structure(unit: cm)
通过Opensees软件对该桥进行有限元建模.由于场地条件为一类,建模时假定墩底与地面固结,未考虑基础的影响.采用弹性梁柱单元(elastic-element)和线弹性材料模拟主梁,采用非线性梁柱单元(nonlinear beam-column elements)模拟主墩和过渡墩,采用零长度单元(zero-length element)模拟支座.有限元模型局部如图4所示.
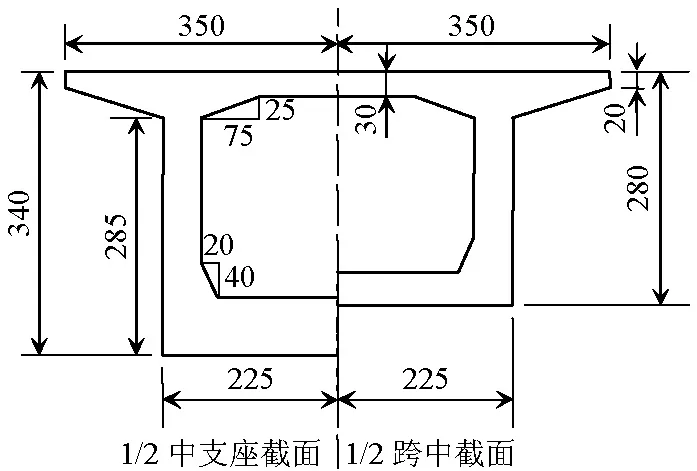
(a) 主梁断面

(b) 1号、4号桥墩截面
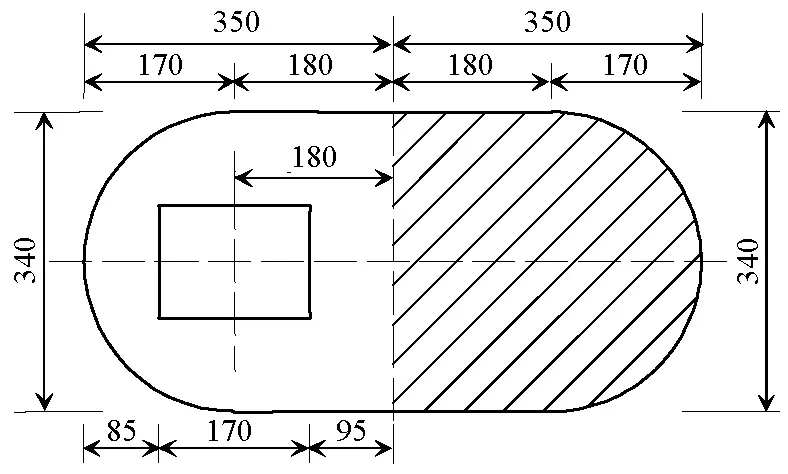
(c) 2号、3号桥墩截面图3 主梁和桥墩截面示意(单位:cm)Fig.3 Section of main beam and pier(unit: cm)
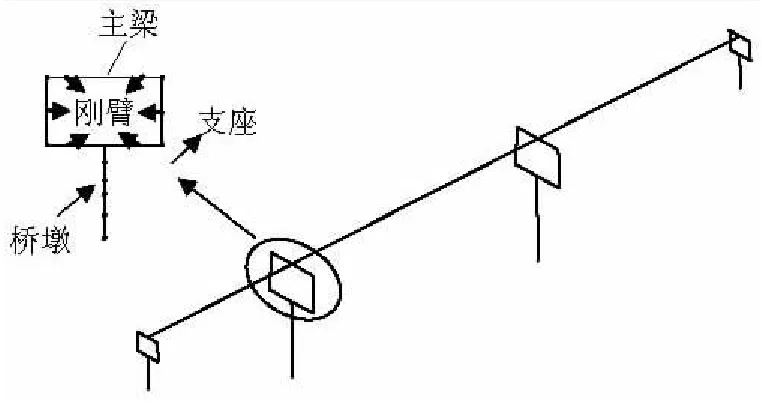
图4 桥梁局部有限元模型Fig.4 Finite model sketch map of pier
采用Opensees中的钢筋(steel01)的本构对其进行模拟.在进行非线性时程分析时,约束混凝土则采用了过镇海模型[14].
采用理想弹塑性单元(elastic-perfectly plastic material)模拟支座本构.支座力与变形关系见图5.支座刚度如表1所示.

图5 支座力与变形的关系曲线Fig.5 Relation between support reaction and displacement
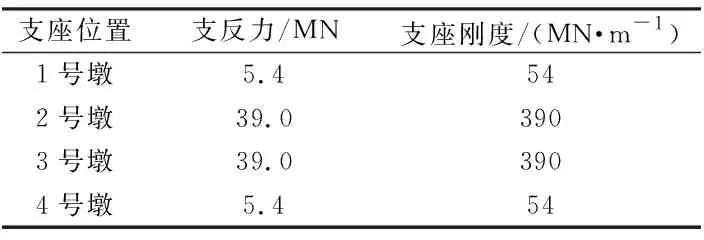
支座位置支反力/MN支座刚度/(MN·m-1)1号墩5.4542号墩39.03903号墩39.03904号墩5.454
3.2 破坏状态定义
在大多数桥梁地震易损性分析中,墩柱延性被作为主要的指标参数来衡量结构的破坏状态.Shinozuka等[15]对同一类型的桥梁墩柱进行了大量分析,归纳出了4种破坏状态:轻微破坏、中等破坏、严重破坏和结构倒塌.根据实际情况,从两个方面定义桥梁结构的破坏状态,即桥墩的破坏和支座的破坏.
3.2.1桥墩破坏状态
以墩底的曲率作为桥墩工程需求参数EDP,不同破坏状态下根据墩底截面的弯矩-曲率曲线中的4个关键点(φ1、φ2、φ3、φ4)确定损伤指标,分别对应桥墩的轻微损伤、中等损伤、严重损伤和结构破坏.
桥墩破坏状态定义见表2.表2中:
φ为墩底曲率;
φ1为受拉区钢筋首次屈服;
φ2为等效屈服点;
φ3为非约束混凝土压溃;
φ4为核心混凝土压溃.
桥墩的损伤指标如表3所示.
由于固定支座设置在3号墩,其曲率远大于其余3个桥墩,所以顺桥向仅给出3号墩的破坏指标.在后期分析中发现对于横向桥地震,桥墩几乎未发生严重损伤和结构破坏,所以在本算例中只选取顺桥向进行分析.
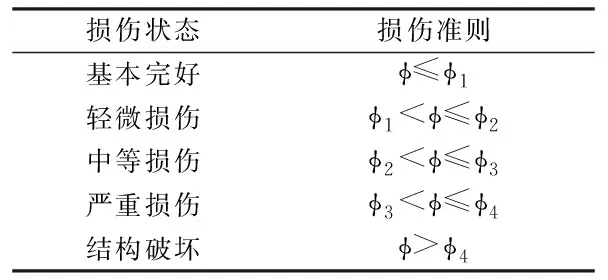
表2 桥墩破坏状态定义Tab.2 Definition of pier damage states

表3 桥墩不同状态破坏指标Tab.3 Different piers damage criteria
3.2.2支座破坏状态定义
本文中连续梁桥活动支座容许位移为150 mm,通过位移来定义其损伤指标,并以位移延性比来定义支座的破坏状态[10].支座破坏状态定义见表4,其中D为支座位移.
3.3 高速铁路连续梁桥整体易损性分析
从太平洋地震工程研究中心PEER(pacific earthquake engineering research center)的地震记录数据库中根据桥址处地质条件选取20条远场地震波记录.采用了IDA方法,选用地面峰值加速度(PGA)作为地震动强度参数,每列地震波经过 10次调幅,峰值加速度从0.1g~1.0g,增幅为0.1g.

表4 支座破坏状态定义Tab.4 Definition of bearing damage states
结构整体而言,桥墩的倒塌以及支座的破坏都可能造成整个桥梁结构的失效.因此,需要综合考虑各个构件的易损性,从而得到整体结构的易损性曲线.在进行整体易损性分析的过程采用一阶可靠度理论来估计结构的失效概率,对于桥梁来说可以认定该结构的可靠度体系属于串联体系,该体系下的桥梁构件破坏处在一个相对独立的状态.
如式(11)所示,一旦结构有部件发生破坏则整体发生破坏.
(11)
式中:
Psys为系统破坏概率;
P(Fi)为构件破坏概率.
绘制结构整体易损性曲线,如图6~9所示.

图6 整体轻微损伤易损性曲线Fig.6 Fragility curve of overall slight damage
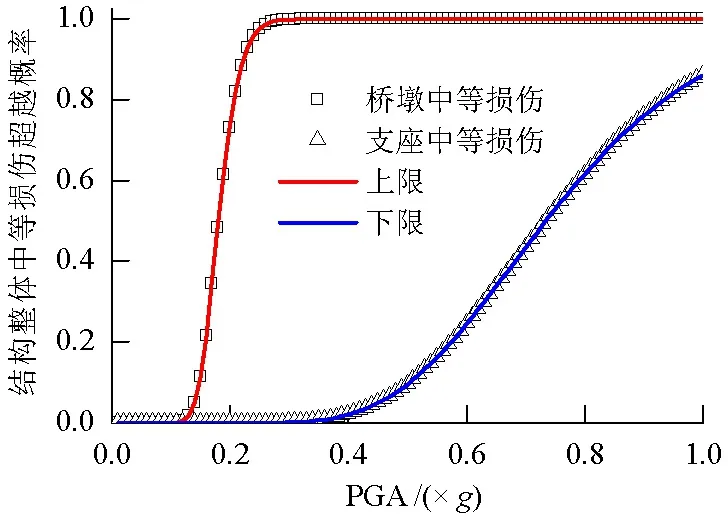
图7 整体中等损伤易损性曲线Fig.7 Fragility curve of overall medium damage

图8 整体严重损伤易损性曲线Fig.8 Fragility curve of overall serious damage
从图6~9可以看出,将桥梁看成一个体系,桥梁体系发生轻微与中等损伤时整体破坏的概率是由桥墩的破坏概率控制,而桥梁体系发生严重和整体破坏的概率则基本是由支座的破坏概率所控制.根据图6~9的结果,可以拟合出式(11)的函数拟合参数,如表5所示.

图9 整体破坏损伤易损性曲线Fig.9 Fragility curve of overall destruction

拟合参数轻微损伤中等损伤严重损伤破坏α1.004 71.005 61.014 01.016 5λ-1.008 9-1.009 9-1.015 9-1.017 3δ1.670 71.778 86.581 48.121 9u10.408 310.414 19.143 98.542 6
3.4 桥址地震危险性概率函数拟合
桥址所处位置抗震设防烈度为7°,根据我国规定,设防烈度为抗震设计基准期50 年超越概率10%的烈度.众值烈度为一定时期内超越概率为63.2%的地震烈度,根据概率论众值烈度为基本烈度减去1.55°,即为7°-1.55°=5.45°.根据式(7)可以计算出形状参数K=8.335.将所得结果带入式(7)可以推导出任意年限(t)桥址所在地烈度概率分布函数.
该桥的抗震设计基准期为100 年,所以可以采用式(12)推导该场地下不同烈度地震的发生概率.
(12)
将求得的结果带入式(9),求解时需要注意加速度单位的换算.可以得到一组地震峰值加速度与发生概率的对应关系,如表6所示.
表6表示桥址处设计基准期100 年内不同超越概率时的地震加速度峰值.式(10)中众值加速度的定义为一定时期内超越概率为63.2%的峰值加速度,根据表6进行拟合可以得出ag=0.573 m/s2.对式(10)两端取对数,对ln(-ln(1-p))和-K(lna-lnag)进行最小二乘法拟合.求出式(10)中的形状系数K=2.703 9.式(10)可推导为
e-(a/0.573)-2.703 9.

(13)
3.5 高速铁路连续梁桥地震风险评估
综上所述,根据以下的流程图,确定出式(6)中的待定参数,可以将桥梁风险概率积分写为
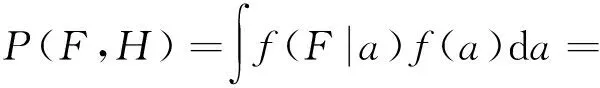
(14)
其中积分前半部分的参数按照表5分情况取用.经过积分计算可以得出桥梁风险概率如表7所示.

表7 桥梁风险概率Tab.7 Bridge risk probability
依据文献[6]中基于国际隧道协会颁布的“隧道风险管理指南”中有关研究成果所提出的桥梁风险评估的风险概率描述进行评价,表明桥梁在100 年设计期内结构进入轻微损伤和中等损伤是可能的,进入严重损伤和完全破坏是基本不可能.
4 结 论
(1) 基于IDA方法得出易损性曲线并进行概率函数拟合,结合地震危险性资料得出地震危险性概率函数,将所得结果采用数值积分的方法进行桥梁地震风险评估是一种可行和有效的方法.
(2) 当地震危险性资料缺乏或不足时可以通过地震烈度分布函数及其与地震峰值加速度之间的换算关系,得出地震加速度峰值概率密度,从而推导和完善地震危险性分析资料.
(3) 对于该高速铁路典型跨径(32+48+32) m 连续梁桥,设计期内结构进入轻微损伤和中等损伤是可能的,进入严重损伤和完全破坏是基本不可能.
