基于Isight与CarSim的H臂悬架C特性稳健性优化设计*

曹开斌廖抒华刘锦武

（1.广西科技大学；2.柳州孔辉汽车科技有限公司）

悬架C特性是指当轮胎受到地面的反作用侧向力、纵向力及回正力矩时，产生悬架弹性变形引起车轮定位参数随力或力矩变化的规律[1-2]。现代大量汽车悬架采用橡胶衬套，而悬架C特性对整车操稳性能有着重要影响[3]。文献[4]研究了麦弗逊前悬硬点对整车操纵稳定性的影响；文献 [5-6]采用了田口方法优化悬架K&C特性；文献[7]运用响应面法对重型商用车钢板弹簧悬架硬点进行优化，改善了悬架的运动学特性；文献[8]基于多岛遗传算法对前悬K特性进行优化，改善了车辆的操纵稳定性。针对样车在底盘调校阶段所存在的整车操稳性能未达到设计目标的问题，以该样车的H臂悬架为研究对象，利用CarSim建立整车模型，并与Isight和MATLAB联合仿真对H臂悬架C特性进行灵敏度分析筛选设计变量。采用RSM法拟合得到系统变量与目标响应之间的近似模型，通过非支配排序遗传（NSGA-Ⅱ）算法对整车操纵稳定性进行多目标稳健性优化，探究一种可改善整车操纵稳定性且为悬架性能开发确定优化指标的有效方法。

1 整车模型的建立与验证

1.1 整车模型建立

通过实测K&C特性试验数据，建立基于CarSim的某乘用车整车仿真模型。CarSim软件主要由模型输入、分析求解及结果输出三部分组成。建模时，输入整车基本参数、发动机参数、前后悬架K&C特性、轮胎、转向及制动系统等总成特性参数信息；空气动力学特性采用系统缺省值。所建整车模型部分参数，如表1所示。

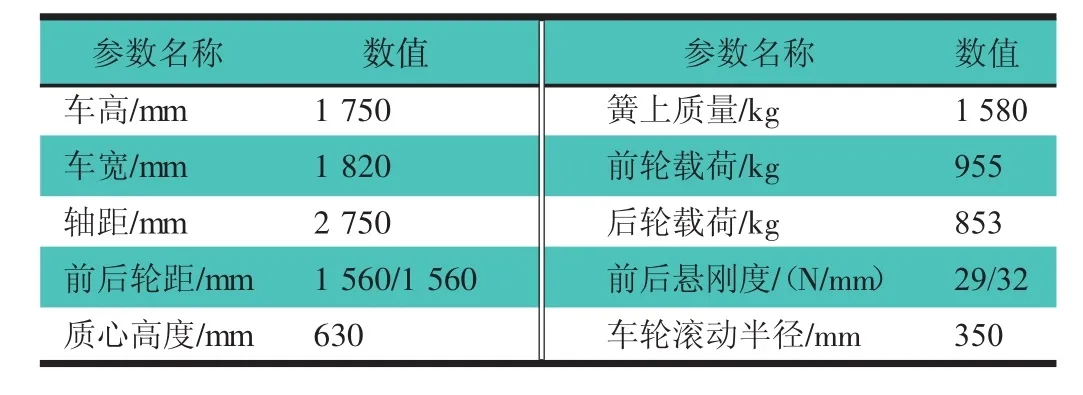
表1 整车模型部分参数

1.2 整车模型仿真与试验验证

按照GB/T 6323—2014《汽车操纵稳定性试验方法》[9]对已搭建好的CarSim整车模型进行仿真，主要包括稳态回转试验、转向盘角阶跃、转向盘角脉冲及蛇行试验等，将仿真结果与实际操稳数据进行对比分析，验证所建模型的准确性。图1示出整车模型仿真与试验结果。从图1可以看出，受轮胎模型与实际模型的差异和转向系统惯量的估算等因素的影响，蛇行仿真工况下的转向盘转角、横摆角速度及侧向加速度曲线与试验曲线存在一定偏差但趋势一致，故可判断此仿真模型是准确可行的。对整车其它工况进行对比分析，结果均可达到满意的精度。

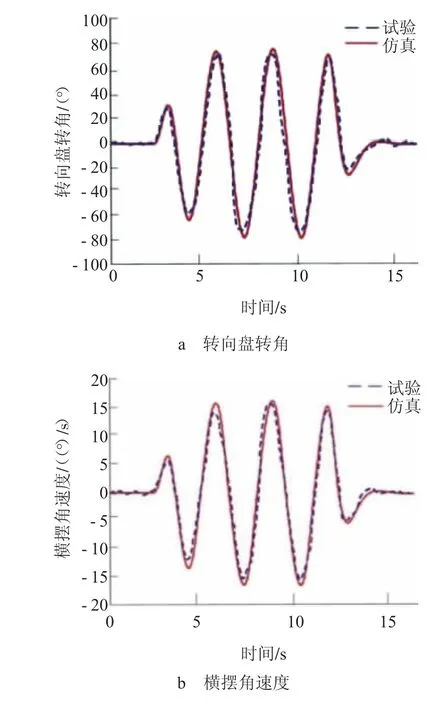
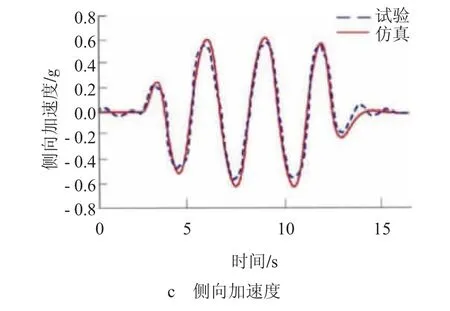
图1 整车模型仿真与试验结果

2 优化原理

Isight是基于参数的多学科设计优化软件之一，利用Isight平台将CarSim以及MATLAB进行集成。在Isight中定义优化参数，给定参数的初始值和约束条件，并根据优化问题类型选择适当的优化算法。MATLAB对优化参数进行一定的前处理，将整车仿真所需的参数传递给CarSim；调用CarSim求解器，采用Car-Sim进行整车仿真试验；选择适当的近似模型，将仿真试验结果进行拟合。依照QC/T480—1999《汽车操纵稳定性指标限值与评价方法》[10]，将评价汽车操纵稳定性指标所需要的参数值（如汽车横摆角速度、侧向加速度、转向盘转角等）从CarSim中输出传给MATLAB进行后处理；再传回Isight迭代优化，实时更新每一步的参数。Isight平台的CarSim与MATLAB集成，如图2所示。

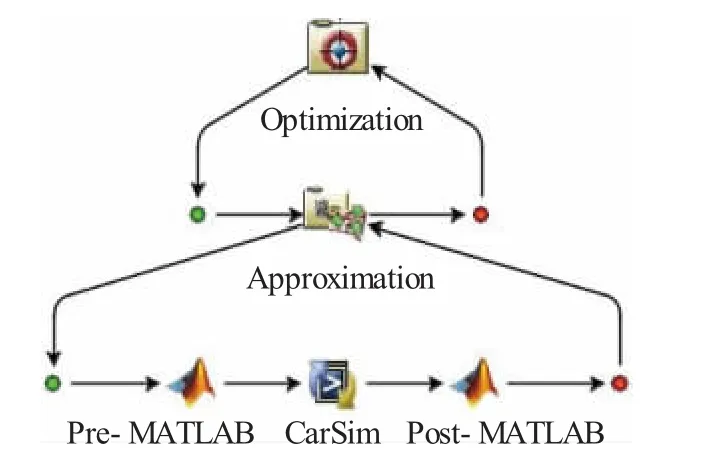
图2 整车基于Isight优化模型图

3 悬架C特性稳健性设计

3.1 灵敏度分析确定设计变量

H臂悬架C特性灵敏度分析通过Isight，CarSim，MATLAB软件联合仿真来完成。在Isight软件中采用Latin Hypercube法进行试验设计，找出对整车在稳态回转与蛇行试验工况下的侧向加速度、横摆角速度及车身侧倾角等影响显著的因素，并根据文献[10]的评价方法在MATLAB中进行评价打分。将H臂悬架C特性作为变量，在稳态回转与蛇行2个试验工况下分析整车操纵稳定性，以稳态回转试验工况的综合评价计分值（Nw）和蛇行试验工况的综合评价计分值（Ns）作为响应目标。对H臂悬架C特性的9个参数进行灵敏度分析，将灵敏度高于10%的参数变量视为影响因子，同时列出影响数量，结果如表2所示。根据竞品车数据库综合考虑设定该H臂悬架C特性的初始值，并将其变化系数作为自变量，初始值为1，其变化域为[0，2]。

表2 某车型悬架C特性灵敏度分析结果

根据表2，将影响数量＞0的参数变量F2，F3，F4，F5，F6，F9作为控制因子；同时考虑到汽车在进行实际试验工况时的状态，把汽车载荷、质心高度及质心离前轴的距离作为噪声因子，其噪声因子水平，如表3所示。

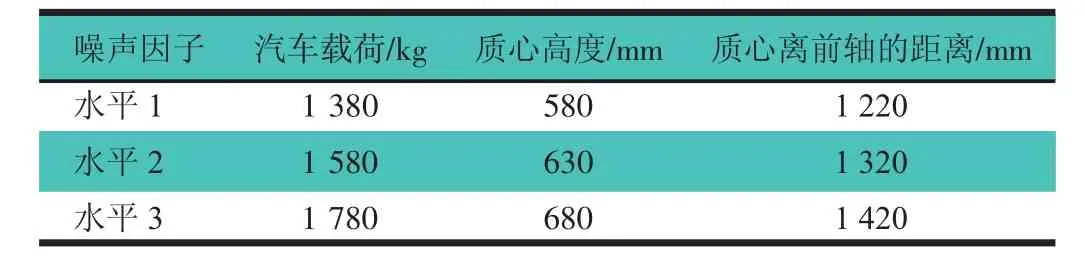
表3 影响目标参数的噪声因子水平

3.2 确定目标函数

3.2.1 稳态回转试验工况

文献[10]中稳态回转试验的评价指标为：中性转向点的侧向加速度值（an）、不足转向度（U）和车厢侧倾度（Kφ），并根据式（1）对各个指标进行评价计分。

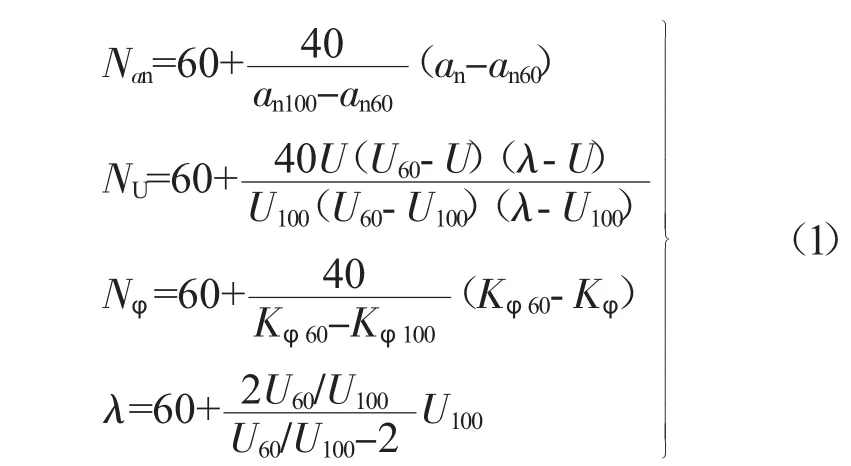
式中：Nan——中性转向点侧向加速度值的评价计分值；NU——不足转向度的评价计分值；

Nφ——车身侧倾度的评价计分值；

λ——比值系数；

an100——中性转向点侧向加速度上限值，m/s2；

U100——不足转向度的上限值，（°）/（m/s2）；

Kφ100——车身侧倾度的上限值，（°）/（m/s2）；

an60——中性转向点侧向加速度下限值，m/s2；

U60——不足转向度的下限值，（°）/（m/s2）；

Kφ60——车身侧倾度的下限值，（°）/（m/s2）。

稳态回转仿真试验进行综合评价计分值（Nw），按式（2）计算：

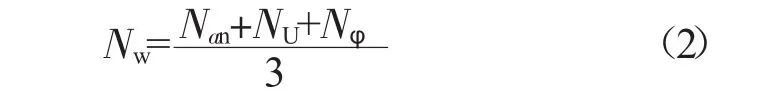
3.2.2 蛇行试验工况

蛇行试验按基准车速（65 km/h）下的平均转向盘转角峰值（θ）与平均横摆角速度峰值（r）进行评价计分。

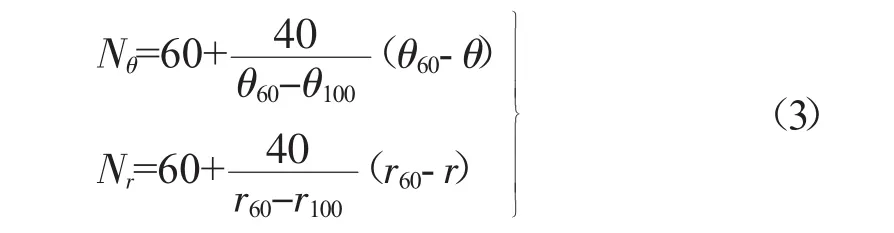
式中：Nθ——平均转向盘转角峰值的评价计分值；

Nr——平均横摆角速度峰值的评价计分值；

θ100，θ60——平均转向盘转角峰值的上下限值，（°）；

r100，r60——平均横摆角速度峰值的上下限值，（°）/s。

Ns按式（4）计算：

将Nw和Ns作为目标函数。要求Nw和Ns越大越好，同时希望Nw和Ns在噪声因子扰动下的波动越小越好。

结合工程经验综合考虑设定Nw和Ns的理想值域为[90，100]。

3.2.3 目标函数的响应面法拟合

根据灵敏度分析的结果，在Isight中采用响应面法分别对Nw和Ns进行拟合，用回归分析后得到的二阶响应面近似模型，表示悬架系统变量与目标响应之间的关系。

Nw的拟合目标函数结果为：

Ns的拟合函数结果为：

式中：x1，x2，x3，x4，x5，x6——前束角/回正力矩、外倾角/侧向力、前束角/侧向力、轮心Y向位移/侧向力、轮心X向位移/纵向力及前束角/纵向力的斜率均值。

通过拟合优度检查拟合效果，拟合的各项指标值，如表4所示。其中，R2和Radj2越接近1，Re值越小，说明拟合优度越高。一般要求R2＞0.9，Re＜0.02。从表4可以看出，拟合效果比较理想。

表4 目标函数的拟合优度指标结果

3.3 基于NSGA-Ⅱ算法的稳健性优化设计

基于3.2.3节中得到的RSM拟合结果，文章采用NSGA-Ⅱ算法，对整车操纵稳定性的评价指标进行多目标优化，其建立的多目标优化模型为：

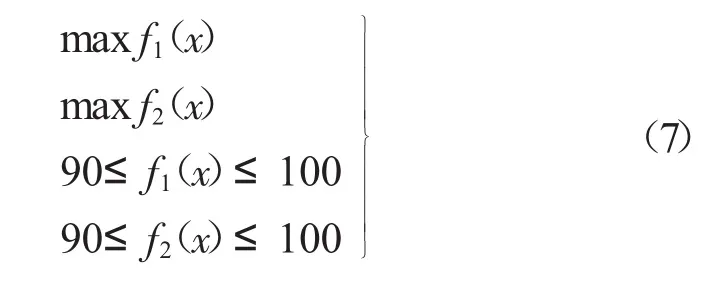
以Nw和Ns的均值最大及其方差最小为优化目标，NSGA-Ⅱ参数设置种群数为40，遗传代数为50，交叉概率为0.9。经过计算分析，得到Pareto最优解集，如图3所示。

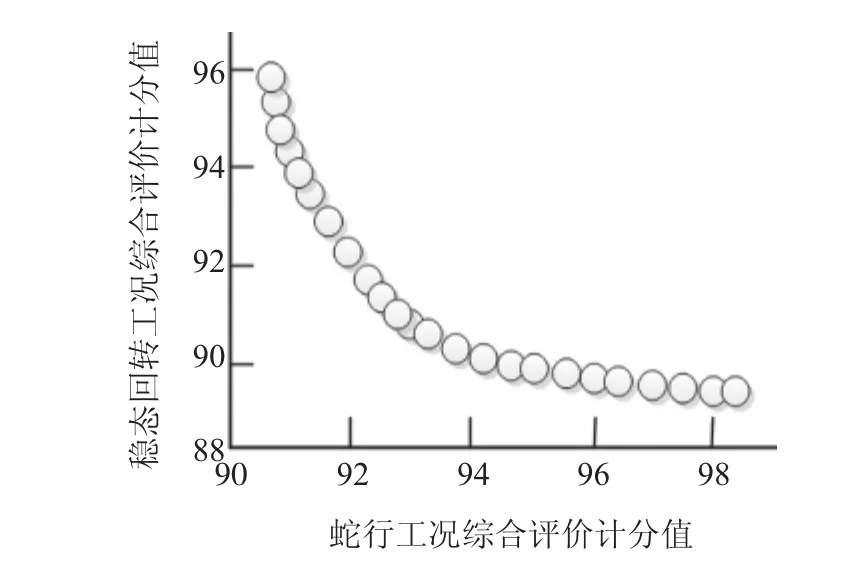
图3 目标函数的Pareto最优解集分布

由图3可知，综合考虑f1（x）和f2（x）之间的关系，在保证不影响悬架其他性能的同时，应尽量小地改动变量参数，从Pareto最优解集的中间段选定本次优化的最终解，其对应的优化变量取值与初始值进行对比，如表5所示。

表5 稳健性优化后设计变量取值

4 优化结果分析与验证

根据稳健性优化结果，与Nw和Ns进行对比分析，如表6所示。从表6可以看出，Nw和Ns的变化均值均在目标值范围内，说明该车的整车操纵稳定性有较大的改善。

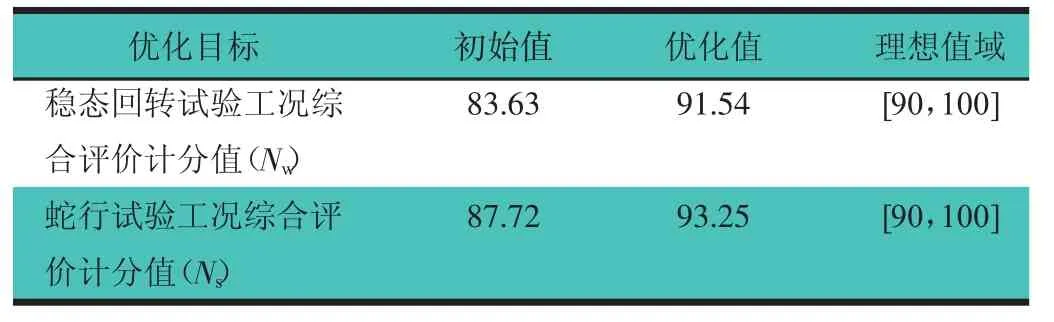
表6 响应目标的优化结果分析

为证明优化结果的有效性，采取1 000个样本点对优化前后的稳健性采用简单随机抽样方法进行蒙特卡罗验证，结果如图4所示。

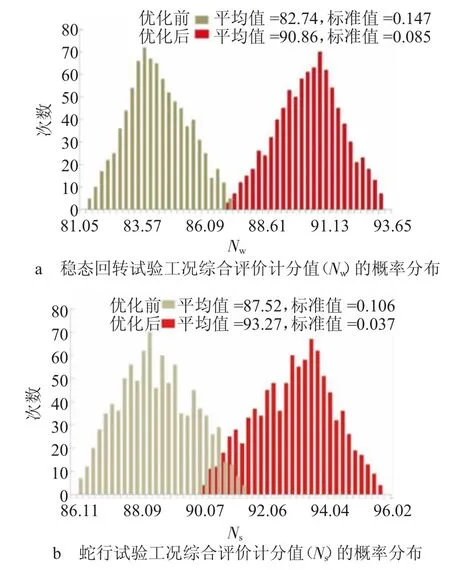
图4 优化前后目标响应的概率分布

从图4可以看出，在考虑汽车进行实际试验工况时的载荷、质心高度及质心离前轴的距离存在实时变化误差的同时，各响应的方差也有所减小，表明优化后整车操稳性能的稳健性有明显提高，证明了优化方法的有效性。

5 结论

1）采用RSM法对目标函数进行拟合，用回归分析后得到的二阶响应面近似模型，表示悬架C特性与目标响应之间的关系；通过NSGA-Ⅱ算法对整车操纵稳定性进行多目标稳健性优化。优化结果达到Nw和Ns的目标值域，同时经蒙特卡罗验证，证明了该方法的有效性。

2）在样车调校阶段，基于Isight平台与CarSim和MATLAB联合仿真的方式对整车操纵稳定性进行稳健性优化设计。研究结果表明，该方法相比于传统的经验法，缩短了调试周期，提高了工作效率，节约了开发成本，同时为悬架性能分析确定优化指标提供有效的指导。