跳起的悬链线:现象、理论和实验
2018-07-11王雯宇许武龙杨旭东
王雯宇 许武龙 许 洋 杨旭东
(北京工业大学应用数理学院,北京 100124)
1 跳起的链子
有这样一个有趣的物理现象如图1所示,高台上的杯子中盘着没有缠绕在一起的一根链子,从杯中拿起链子的一端,让它沿着杯壁外侧自由下落,下落的一端带动杯中的链子掉落到地面上。下落过程中链子并不是一直贴着杯壁下落,而是很快地从某个时刻起,链子跳起来,在空中有一段时间会维持较为稳定的弧形形状。这个实验经常在大学物理课上演示。从现象上看这是一个非常有趣的经典力学问题,具体过程可以参看网络视频①https://v.qq.com/x/page/o0363pisyik.html?。本论文就试图分析研究掉落的链子(下面称之为“掉链线”)的形状、下落高度、跳起高度、跳远距离之间的关系等。在理论分析之后,我们将做实验来验证理论。

图1 跳起的链子现象示意图
2 现象及理论分析
2.1 实验现象
首先我们说明一下实验的发生过程。如图1所示把链子一层层盘绕放入杯子中,链子之间不互相缠绕(实际过程中很难做到这一点,而这也是影响实验的关键因素之一)。然后将杯子放置一定高度,从杯中取出一小段链子让其自由下落,很快链子就与杯口分开,从杯中跳起。在实际的操作过程中我们也尝试了用一根柔软几乎不可收缩的绳来做相同的实验,绳子也可以勉强跳起但现象很不明显,所以实验通常采用细金属条串起金属球的链子,金属球之间可以松弛连接,且松弛连接时,链子没有抗弯能力,这一点是链子与柔软绳子的关键差别,下文我们将通过分析指出其原因。
实验发现链子从杯中跳起到最高点过程中,由于杯中链子缠绕方式复杂,起跳点持续变换,因此从杯中上跳到最高点过程的形状也非常复杂。而在最高点到落地点这一段,在最高点附近链子会维持一个较为稳定的形状。落地点链子在地上不停地堆积和缠绕造成链子的形状会发生抖动,但是由于起跳高度远小于下落高度(后文详述这些高度的定义),在地面的抖动并不影响最高点附近的稳定形状。
综上观察,我们认为这个物理现象可以分为链子跳起过程和链子悬空稳定形状两部分来分析。由于稳定形状过程是大多数读者所关心的,而且根据我们的分析,发现其实这也是该现象问题的关键,所以这一节我们对此稳定形状进行专门理论分析。
2.2 悬空稳定形状分析
乍一看,跳起的链子形状像是抛物线,其实问题并不是那么简单。因为一个质点斜抛做自由落体的运动轨迹是一条抛物线,而对一个不可伸缩的链子来说,悬空的链子上每一个链元的速率是一样的,并不是在做匀变速运动。根据我们的观测,杯中链子消失速度基本上是恒定的,因此我们假设在理想情况下悬空的链子每个链元的速率为v0,那么在d t时间内,有λv0d t质量的线元(λ为线密度)速度从零加速到v0,则A点的链元就受到了静止在杯中的链子拉力,为

注意这只是理想情况,下面研究表明,A端受力小于λv20。B点速度为v0的链元碰撞地面,如果链子完全弹性碰撞则会以v0从地面弹起来,同样的分析表明B点链元受到地面的冲力等于2λv20。当然由于地面链子的拖拽,链子与地面不是完全弹性的,后文将给出处理B点冲力的具体方法。这样悬空链子就处在一个理想状态,即在TA、TB张力的作用下,保持速率为v0,d t时间内把杯中λv0d t的链子从杯中挪到地面上,即重力势能转化为动能,动能转化为链子和地面的内能。
理想的状态下,研究表明悬空的链子形状其实就是一个倒着的悬链线。这里首先简单说明悬链线形状的推导过程。如图2所示,在一面墙上A、B两点之间挂起一根不可伸缩的链子,链子的形状就被称为悬链线。悬链线形状的推导过程是经典力学乃至数学历史上一个重要问题[1-3]。牛顿力学中受力分析的方法可以计算其形状,而后发展起来的分析力学有更加简洁的推导过程。对一个函数的变分实际上还推动了泛函分析的发展,具体历史过程因为不是本文的重点,所以就不展开说明了,感兴趣的读者可以阅读相关参考文献[4]。假定链子的形状为

图2 悬链线示意图

变分原理其实就是要找到一个y(x)使得链子势能或者重心处于最低点。整个系统作用量为

其中,g是重力加速度;c是任意一个常数(因为链子可以挂在任何高度,势能零点也可以任意选取);y′是y的一阶导数;1+y′2d x是一个线元的长度;L就是系统的拉格朗日量

分析力学中根据L的运动方程[5-6]

求解悬链线的形状,即

化简可得

这是一个非线性的微分方程,其解为

其中a,b是待定常数。以上就是通常分析力学中的悬链线求解过程,注意此时我们取的是任意高度的悬链线,所以有个待定参数c。其实读者还可以注意到虽然运动方程(6)是非线性的,但是它有一个分立对称性,即做变换
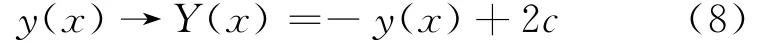
Y(x)也是悬链线方程的一个解。而由于通常挂着的链子都受到重力作用,链子都是向下凹陷的,所以这个翻转之后的解看上去没有应用。或者说这个解是系统的另外一个极值点,该点不是稳定点,也就很少有人来讨论此事。而我们分析发现,这个翻转之后的解恰好就是掉链线的形状。
对于悬空链子的作用量,其实只需要加上动能项,而势能项与悬链线是一样的。

即拉格朗日量为


而已。因此根据实际情况,跳起的链子向上凸起,可以得到

这就是掉链线形状的函数。
2.3 经典力学的检验
上一小节中掉链线运动方程推导过程与一般的悬链线求解过程不同之处在于悬空链子每个链元实际上是处在运动过程中,链子不断从杯子中跳出,又掉落到地面上,这是一个变质量运动系统,因此可能有读者会疑问以上变分原理能否适用。其实我们也可以根据牛顿力学的受力分析得到完全一样的运动方程。悬空链子在链内存在着张力

链中张力在链子上任意点都是沿着切线背离链元方向的,如图3所示。此时我们约定取A点指向B点的方向做为正方向,即研究链元靠近B点一端的张力。因为每个链元在做曲线运动,速率不变,所以每个链元的切向加速度为零。如图3所示,d T和链元的重力沿切向分量相消,即


图3 掉链线所受张力分析图
因此链中张力可以表示为

这是个非常有意思的结果,即稳定形状链子中的张力随着链元的高度改变而改变,其实这也与悬链线中的张力情况是一样的。为了清楚地表示受力分析,我们采用了图3所示的分析办法,即研究x-d x,x,x+d x两段链元的受力。由于这两段链元在同一点x附近,线速度相等,忽略高阶小量曲率半径也相等,所以可以放在一起写一个统一的向心力方程。每一个链元法向向心力应该由重力以及张力T曲线法线方向分量来提供,而链元两侧张力的改变微元d T,其法线方向分量是高阶小量,计算向心力的时候可以忽略。x和x+d x点切向夹角分别为θ和θ+dθ,则

由此可得

x-d x和x之间链元分析与此类似,因此向心力为

加上重力的法向分量,则x-d x到x+d x之间链元的力学方程为(两段链元之间的张力是内力)

其中ρ为x点曲率半径

代入曲率半径ρ、dθ、张力T,计算可得

由于线形上凸所以

化简整理之后可得

因为TA是待求变量,所以不妨定义

则y的力学方程为

这就是悬链线的微分方程,与公式(3)完全一样。由上可知,牛顿力学和分析力学都可以得到链线的形状为悬链线的结论。
相比于分析力学变分原理,牛顿力学的分析虽然复杂一些,但由于是力的分析,所以物理图像更为直观。我们还可以看到悬链线和掉链线两端受力情况是不同的。当选定研究链元靠近某一端的张力后,图2中静止的悬链线两端张力方向是相同的,而图1中,A端链元是处于加速过程,B端链元处于减速过程。选定研究链元靠近某一端的张力后,则两端张力是沿着相反方向的。形象地说就是悬链线是两端钉子向相反方向互相拉着的一个稳定系统,而掉链线是两端朝着线的某个方向推着的“稳定系统”。
2.4 起跳分析
这里先说明一下,TA≠λv20的原因。TA=对应的其实是理想情况,即每个链元瞬间速率从零加速到v0,而实际情况则是链子松弛盘绕,链元需要一段加速过程到v0,使得TA实际上是小于的。数学解析上看,如果c=0,掉链线形状为

此时

不能得到一个y>0的解。对于一个非线性微分方程来说,方程的解加上某个常数不再是方程的解。所以如果假设了图4的坐标系统,得到y>0的解的话,c必须不为零,根据公式(21)也可以看到TA必须小于λv20。因此下面我们按照图4所示坐标,补充链子的加速过程,(C点到A点)加速跳起过程高度表示为hi。掉链线跳起高度为hr,则总跳起高度为

图4 掉链线起跳过程分析图

链子下落为H,跳远宽度为2x0。我们将进一步研究跳起这些量之间的关系,并尝试做实验来验证。
A点张力为

根据公式(14),A点到B点张力T的方程为

上文已经说明完全弹性碰撞时B点受力等于2λv20,有读者在这里会疑问B点张力的合理性,因为B点与A点类似,需要一个减速过程,而且最后静止于地面上,张力值应该小于λv20。但是由于链子落地过程不能人为控制,我们发现落地过程中链元还会轻微弹跳,所以实际上链元对地面的冲力会大于λv20。为了准确起见,不妨引入一个系数α(假定它为一个常数)来描述B点的受力。因此

α的具体值应该大于1小于2。注意,这里我们选定正方向,所以B点受力为负值。由于实验中H远远大于hj,因此,B点张力的涨落其实对物理结果是不敏感的。由此

这就是下落高度与悬空链子速率之间的关系,当然这里面还有两个待定的参数c,α。稳定掉链线起跳高度y(x=0)处

由此问题转变为研究参数c、a和α上。3.1节在实验分析阶段再对此做详细讨论,在此之前,我们首先来分析一下加速过程。
加速过程速率随时间改变,看上去问题似乎有点棘手。分析之后,发现其实时间参数也可以去掉。速率表示为v,根据图3和公式(14),简单分析链元切向加速度就可以得到其力学方程为
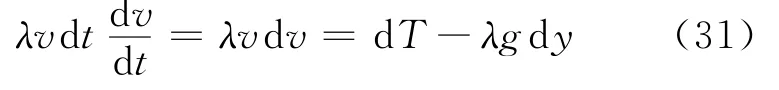
注意,此时由于链元松弛连接,可以不用考虑法向力学方程。可以看到,刚好可以约掉d t。这其实就是掉链线过程中重力势能转换为动能的数学表述,方程两边分别积分得到
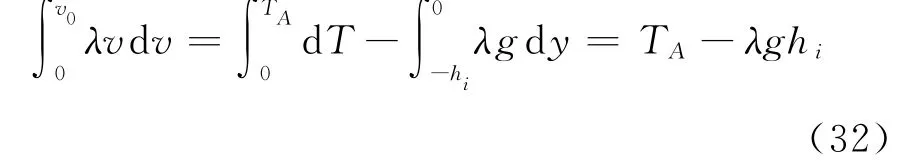
因此
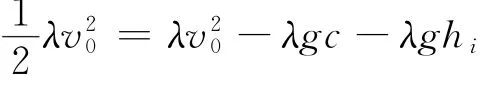
即

再代入公式(29)可得

由此还得到了系统起跳的条件,如果这个过程可以发生,我们必须要求hi得大于零,因此起跳条件为

而链子跳起的总高度

到此,我们就可以看到,链子跳起的高度基本上与链子跳落高度H呈线性关系,当然参数c,a和α还有待确定。
3 实验验证
3.1 实验分析以及过程
有了第2节的理论分析,我们就可以用实验来做验证了。但是需要说明的是,第2节分析的情况是理想状态,而实际实验存在很多难以克服的困难,主要有:
(1)理想情况下,杯子中的链子完全松弛,而实际上很难做到这一点。正如上节开头所说,链子上小球难免会有缠绕,这就造成了链子起跳和稳定过程中,链子质量不是均匀的。我们发现这一点对实验影响非常大。一个小小缠绕扭结就使得线形改变。
(2)理想情况下,起跳点和落地点都是固定,这样可以得到稳定的图形。但是实际过程中,起跳点和落地点都在不停抖动,线形也在抖动,很难测量线形的准确形状。因为掉链线是一个指数函数,y随着x迅速增长,所以抖动线形下部基本就是一条直线,要准确对应指数函数曲线非常困难。
(3)由于以上两点,准确确定A、B、C点的位置也有问题,基本上只能在有很大误差的情况下确定hj和H。
虽然存在以上困难,但是有一点可以确定,就是

跳起高度hj和c,a在一个量级。基于此,我们认为跳起的链子形状看上去“很像”翻转的悬链线,而实验首先应该验证的是公式(36)中hj和H的线性关系,以及参数α的确定。
具体实验方法如下:我们用3 m的卷尺在白纸上手工绘制了2.5 m的刻度尺贴到墙上如图5(a)所示。然后从200c m的高度逐次以5c m的高度差下降,重复进行掉链实验直到100c m。随着链子下落高度降低,起跳高度下降很多,测量也越来越困难,因此我们选定10c m的高度差下降记录链子下落过程一直到40c m。在每一个位置处我们用一部手机拍摄掉链视频。拍摄过程中手机镜头尽量平视链子使最高点出现在手机的正对面,记录整个过程。在实验过程中存在着很多因素导致很大的误差,每一个位置我们都是多次拍摄以寻找最佳视频。

图5 实验装置以及器材
实验用的杯子和链子如图5(b)、(c)、(d)所示。具体的参数如下

金属球直径 5±0.5 mm金属细杆长度 3±0.5 mm链子长度 8.4 m链子线密度λ 0.036±0.03kg/m杯子高度 95±0.5 mm杯口直径 66±0.5 mm
分析发现,c,a和杯子口径在一个数量级上。其实原则上讲,只要满足第2节所述理论,任意形状的掉链线都可以存在。但由于链子从杯中跳起,所以跳起链子掉链线形状其实依赖于一定的初始条件,即杯子口径,起跳时刻、起跳点杯中深度等因素。所以同一高度跳起的掉链线形状尽管不是唯一的,但是c,a参数应该是基本上相等,这也是后文得到的线性关系的重要原因。
数据采集过程如下:我们用视频软件对视频一帧一帧观察,寻找视频中某个最佳时刻:掉链线最高点而且形状也稳定,如图5(e)所示。在每一个高度我们截取了稳定清晰的一张图片,记录相应的开始高度位置和起跳高度位置等。估计误差然后用excel表格记录。有了这些数据之后我们就可以进行数据分析了。需要说明的是,受限于实验条件,读数的误差也比较大,所以下面我们更为关注定性结果。
3.2 数据处理以及结果分析
实验结果如图6所示,图中显示了所有采集的数据点。从数据上可以看出当跳落高度H小于100c m时,起跳高度hj非常不稳定,很难看出线性关系。但是当高度大于100c m后,H和hj基本上成线性关系。因此我们认为实验部分验证了第2节的理论推导。
下面就是分析具体参数α的值,由于H较小时,误差很大,所以我们舍去了H小于100c m的数据点。同时,当高度过高时,链子跳落速度v0会过大,造成链子连接过紧而使得上文推导时假定的链子可以任意形变的条件不再成立。所以我们也舍去了200c m和195c m的两个点,另外剩下的数据点有一个明显偏离线性,我们认为它来源于实验中的随机因素,也舍去了。所有舍去的点在图中用灰色×表示,剩余的黑色的点拟合的线性关系在图6中用实线表示,其延长线用虚线表示。由图中实线以及相应数据点,最终得到

可以看到,不确定度很大,而且α的中心值超过了2,但是基于以上众多误差产生的可能性,我们认为α的数值还是符合预期的。另外一件有意思的事情就是,当图中实线延长后与横轴交点会大于零,而这一个点对应的就是公式(35)表示的起跳条件。当然因为随机因素太多,这个起跳条件只能用于大略估计。
最后我们补充说明一下细绳难以跳起来的原因。链子的每个链元是松弛连接的,而细绳很难做到这一点。(因此细绳也很难挂出准确的悬链线形状。)也就是说,起跳要求的无法向力干扰的加速过程(公式(31))条件很难实现,这也就是细绳跳起很难的原因。
4 结语
从高台杯子自由下落的链子跳起来是一个非常有趣的现象,我们把跳起链子分为稳定形状和起跳过程两部分来分析。变分原理和受力分析都表明其动力学方程是一个翻转的悬链线。我们研究了起跳条件,描述链子形状的参数,得到了跳落高度和跳起高度之间呈线性关系的结论。最后我们实验验证该结论,并确定了落地点受力参数α的大小,基本符合预期。
这是一个既有理论又有实验演示的有趣过程。大学物理课堂上给学生演示跳起链子实验之后,可以接着给学生扩展讲解变分原理,悬链线的计算等等,相信可以取得较好的教学效果。落地点受力参数的值对研究一些掉落系统的问题有一定的参考作用。
