基于车辆动力学和改进AGREE算法的高速列车稳定性综合可靠性分析*
2018-07-11曾元辰张卫华宋冬利
曾元辰, 张卫华, 宋冬利
(西南交通大学 牵引动力国家重点实验室, 成都 610031)
高速列车的可靠性高低直接影响车辆的服役质量和运维成本,是车辆设计、制造、运用、维修等各阶段的重要目标。可靠性建模可以建立系统可靠性逻辑关系和数学关系,是系统可靠性分析的基础;可靠性分配可以实现系统顶层可靠性要求向底层的分解,是车辆和零部件设计制造的重要反馈;基于可靠性模型及可靠性分配可进一步指导以可靠性为中心的维修决策优化。
高速列车是个复杂机电系统,随着RAMS理念的发展,当前高速列车系统综合可靠性分析的相关研究已取得了初步的成果。王华胜等[1]、宋永丰等[2]分别对CRH2型动车组、CRH3C型动车组牵引传动系统进行了可靠性建模,并采用评分分配法进行可靠性分配;张安[3]、朱爱凤[4]针对地铁车辆,分别研究了基于历史故障数据的迭代分配方法和比例分配法;陈凌羿[5]在传统可靠性分配方法的基础上,针对多种机车、地铁车辆,提出了基于可信性理论的改进方法;孙超[6]等基于历史故障数据研究了城轨车辆走行部维修周期优化模型。但总的来说,轨道交通车辆的可靠性分析方法还十分简单,顶层指标体系不够明确,可靠性分配往往带有主观经验的因素,这些都限制了可靠性分配方法的推广和应用。
与传统的电气系统或机械系统不同,高速列车稳定性是以车辆动力学为基础的系统级性能,与车辆服役的安全性、舒适性息息相关,同时高速列车稳定性相关因素和影响过程复杂多变,很难通过传统方法开展可靠性研究。文中创新性地将动力学研究与可靠性研究融合,建立高速列车稳定性系统可靠性模型,选择车辆稳定性作为高速列车系统可靠性分配的顶层指标,基于车辆动力学理论对传统AGREE算法进行改进,综合考虑各单元工作时间、重要度、复杂度、历史累计失效率等因素,对高速列车稳定性系统进行可靠性分配,并进而基于可靠性模型和历史失效规律开展维修周期优化。
1 高速列车稳定性系统综合可靠性分析方案与可靠性建模
1.1 高速列车稳定性系统综合可靠性分析总体方案
图1是高速列车稳定性系统综合可靠性分析的研究思路。首先由高速列车结构和系统动力学理论、高速列车运用维修历史失效记录确定高速列车稳定性相关零部件参数及其失效模式,进而建立高速列车稳定性系统可靠性模型;然后针对高速列车稳定性要求开展可靠性分配,基于高速列车动力学仿真模型开展正交试验计算各单元重要度,基于高速列车结构计算各单元结构复杂度,基于历史累计失效规律模型计算各单元的历史失效度,进一步基于改进AGREE算法,综合考虑各单元的重要度、结构复杂度和历史失效度计算各单元分配的可靠度;最后根据可靠性模型以及单元历史失效规律,开展以可靠性为中心的车辆维修周期优化。

图1 研究方案流程图
1.2 高速列车稳定性动力学模型
转向架是保证高速列车良好动力学性能的核心系统,文中以国内外主流结构的高速列车转向架为研究对象。车辆动力学模型是研究系统各状态参数与车辆运行性能映射关系的重要工具,根据车辆系统动力学理论[7],高速列车整车35自由度振动方程为:
(1)
其中,X为系统各自由度振动的广义位移向量,M为系统质量和惯量矩阵,Cs、Cr分别为悬挂系统和轮轨作用引起的阻尼矩阵,Ks、Kr分别为悬挂系统和轮轨作用引起的刚度矩阵,B为轨道输入矩阵,u为轨道不平顺向量。
高速列车稳定性是车辆动力学性能的关键,是一个多因素耦合作用的复杂非线性问题,车辆稳定性不佳的故障表现主要是车辆运行过程中发生横向失稳。车辆横向失稳是轨道交通车辆的特有现象,是轮轨蠕滑作用下外界输入能量不能被系统有效耗散所导致的一种自激振动[7]。车辆横向失稳的主要表现是轮对横移与摇头耦合的蛇行运动,进而通过悬挂系统引起转向架构架或车体的严重横向晃动。大幅的车辆横向失稳会导致轮缘频繁贴靠撞击钢轨,同时会导致车辆和轨道结构的剧烈振动,影响列车运行安全。
临界速度是表征车辆稳定性优劣的主要指标,临界速度越高,稳定性裕度越大,车辆的稳定性越好。临界速度是指车辆提速运行至发生横向失稳的速度临界值,试验或仿真确定车辆临界速度的方法为在直线轨道上,初始设置一段实测轨道谱的不平顺激扰,其后设置为理想平顺轨道,被试验车辆以从低到高的速度运行,观测车辆驶入平顺轨道后轮对横向位移的敛散情况,如图2所示,以出现等幅振荡,即蛇行失稳现象对应的速度作为临界速度并记录[8]。

图2 临界速度的确定方法
1.3 高速列车稳定性系统可靠性模型
根据车辆动力学研究成果[7-9],影响高速列车稳定性的主要动力学参数包括轮对等效锥度、一系纵向定位刚度、一系横向定位刚度、二系回转角刚度、二系回转阻尼、二系横向刚度、二系横向阻尼等,对应的转向架相关部件主要包括轮对、转臂、空气弹簧、抗蛇行减振器、二系横向减振器。结合我国高速列车运用检修过程中的历史故障记录,进一步确定高速列车稳定性8个关键影响参数及其对应的失效类型和维修措施见表1。

表1 高速列车稳定性关键影响参数集
根据车辆稳定性理论,高速列车稳定性是一个多因素耦合作用的功能系统,不能由转向架的物理结构得到系统的可靠性模型,系统中任何一个参数失效都有可能但又不必然导致车辆横向失稳的发生,因此采用等效串联模型描述高速列车稳定性系统的逻辑关系,如图2所示。高速列车稳定性系统可靠性模型中每个单元失效将以一定的风险引起系统失效,该模型考虑了系统中各参数的数量,同时考虑了现行高级修周期内包含多个车轮旋修周期,每个轮对只工作1个旋修周期。

图3 高速列车稳定性系统可靠性逻辑关系
根据高速列车稳定性系统的逻辑关系,考虑各单元的数量、重要程度、工作时间,建立高速列车稳定性系统可靠度分析模型为:
Rs(ts)=Π[1-Ei·(1-Ri(ti))]
其中,Rs(ts)表示系统工作ts时间的可靠度,Ri表示第i单元工作ti时间的可靠度,Ni表示第i单元在等效串联系统中的数量,Ei表示第i单元失效引发系统失效的风险(即下文的重要度),与各单元失效模式、故障程度和失效影响有关。
2 基于改进AGREE算法的可靠性分配与维修周期优化
AGREE可靠性分配法是由美国国防部电子设备可靠性顾问团提出来的经典方法,考虑了各单元的复杂度和重要度,同时也考虑了单元的工作时间,也称作按单元复杂度及重要度的代数分配法,是一种准确有效的可靠度分配方法。近年来,李威伟[10]、向宇等[11]、姜悦岭[12]等针对其他几种工业系统,针对重要度、复杂度的计算方法提出了多种改进方案,但仍然不适用于高速列车稳定性系统的可靠性分配,且均未考虑历史累计失效率的影响。因此,基于传统AGREE可靠性分配算法进行改进,提出重要度、结构复杂度和历史失效度的计算方法,同时考虑单元工作时间进行可靠度分配,进而研究基于可靠度分配结果及历史累计失效规律的维修周期优化方法。
2.1 基于正交试验与极差分析的重要度算法
定量描述各单元的重要度是系统可靠性分配的基础,在可靠性理论[13]中,描述单元的重要度包括结构重要度、概率重要度、临界重要度、B-P重要度等多种方法,但这些方法均要求系统的结构函数可知,这对高速列车稳定性这个复杂系统是很难实现的。同时,实际列车服役过程中失稳发生记录样本量不大,且缺少诱因的诊断结果,难以从统计的角度描述各参数的概率重要度。因此研究重要度的间接计算方法,对于高速列车稳定性来说,车辆的临界速度是表征车辆稳定性的重要指标,单元失效导致临界速度的降幅越大,则车辆越易发生失稳,因此该单元就越重要。因此,可以用参数变化引起临界速度的变化程度定量描述参数的重要度。
进一步确定各参数的变化范围和取值对研究各参数变化对车辆临界速度的影响至关重要,最合理的方法是对列车服役过程中大量失效零部件进行参数测定,获取各参数的分布规律,进而借鉴全局灵敏度分析[14]的方法研究各参数的重要度。当数据条件不足以支持上述工作时,可大致确定部件失效时参数的变化范围和取值水平,借鉴局部灵敏度分析方法[15-16],通过整车台架试验或数字仿真,采用正交试验法确定各参数对车辆临界速度的影响。正交试验是根据均衡分布思想,运用组合数学理论构造正交表格并安排试验方案,考虑了各因素的相互耦合作用,具有正交性、典型性以及综合可比性等优点[17]。正交试验方案的设计已有成熟的数学方法,故在此不再赘述。
进一步采用极差分析法确定各因素对试验指标的影响程度[16-17],因素i的极差Ri的计算式为:


2.2 结构复杂度与历史失效度算法
单元结构复杂度的定义是单元所含重要零件个数占系统重要零件总数的比值,该定义的含义是认为各单元由若干重要零件串联组成,其含有重要零件数越多,故障风险越高,所分配的可靠度越低。但划分和统计车辆稳定性各参数的重要零件数存在困难,因此从重要组件的角度定义各参数结构复杂度计算方法为:
其中Ci为第i单元的结构复杂度,Ni为参数所含重要组件数,∑Ni为系统重要组件数总和。该方法得到的结构复杂度不够精确,但重要组件数方便划分和统计,可操作性强。
下面提出单元历史失效度的概念和计算方法。历史失效度是建立在单元历史累积失效率的基础上,历史失效度越高,表示该单元可靠性较差,因此分配的可靠性可以较低。采用生存分析方法[18]对各故障模式的历史失效数据进行可靠性分析,考虑删失数据的影响,得到各失效模式可靠度与运行里程的散点,并用经验分布函数进行拟合,得到历史累计失效规律Fi(t),并可进一步计算得到现行维修周期下的可靠度Ri。该分析的方法比较成熟,在此不再赘述。因此,定义单元历史失效度的计算方法为:
2.3 改进AGREE可靠性分配
传统AGREE算法的基本原理和分配算法如下:
[Rs(ts)]Ci=1-Ei·(1-Ri(ti))
其中Rs(ts)表示系统工作ts时间的可靠度;Ri(ti)表示第i单元工作ti时间的可靠度;Ci为第i单元的结构复杂度;Ei为第i单元的重要度。
基于文中单元重要度、结构复杂度、历史失效度的定义和计算方法,改进后的AGREE可靠度分配算法为:
其中ωCi+ωFi=1
其中ωCi和ωFi分别为第i单元结构复杂度和历史累计失效率的计算权重,可灵活选取。
2.4 以可靠性为中心的维修周期决策
进一步根据系统可靠性模型和历史累计失效规律Fi(t),优化系统的维修周期 :
考虑到高速列车运用维修的实际情况,保持高级修周期Ts与车轮旋修周期Tw的整数倍关系,即:
Ts=k·Tw,k=1,2,…
则系统维修周期Ts及车轮旋修周期Tw的优化算法为:
其中Fw(t)为轮对的历史累计失效度函数;Rw为轮对可靠度;Ew为轮对可靠度;i代表除轮对外其他单元。
3 算例:CRH380B/BL型高速列车稳定性综合可靠性分析
CRH380B/BL型高速列车是我国当前服役动车组中的主力车型,其转向架结构如图4所示,采用的是经典的高速列车转向架设计。同时现行三级修周期是120万km,车轮旋修周期是20万km。

图4 CRH380B/BL型高速 列车动车转向架
现基于表1中8个关键影响参数和图3中的等效串联系统可靠性模型,对CRH380B/BL型高速列车稳定性系统进行可靠性分配和维修周期优化,要求车辆运用一个三级修周期,发生横向失稳的累计频率不超过1%,即可靠度要求0.99。
3.1 各参数重要度计算
根据动车组运用检修规程,以及相关文献的研究结果[8],确定CRH380B/BL型高速列车服役过程中各参数的5个水平如表2所示。其中动车组运用过程中同轴轮径差限值为1 mm,实际出现最大为2 mm左右,故取0~2 mm范围内共5个值;转臂以及减振器节点均为橡胶件,其刚度参数正常波动约在名义值±40%范围内,同时取-60%为其失效工况参数;空气弹簧刚度参数正常波动约在±20%范围内,同时取-35%、-50%为其失效工况参数;减振器阻尼参数正常波动约在±20%范围内,同时取-30%、-50%为其失效工况参数。
基于8个关键参数的5个取值水平,构造8因素5水平的等水平正交表L50(58)如表3所示(部分),共安排50次试验。

表2 参数各水平取值

表3 L50(58)正交试验设计(部分)
数值仿真技术是研究形如式(1)的复杂多体动力学系统的有效手段,采用多体动力学仿真软件SIMPACK建立所研究的CRH380B/BL型动车组的动力学模型,如图5所示,包括车体、构架、轮对、悬挂元件和轮轨接触单元,同时充分考虑了悬挂元件的非线性特性。

图5 CRH380B/BL型高速列车 动力学仿真模型
采用第1.2节中的试验方法确定车辆在各工况的临界速度,进而通过2.1节中基于极差分析的重要度计算方法,计算得到的各参数重要度见表4。

表4 各参数重要度计算结果
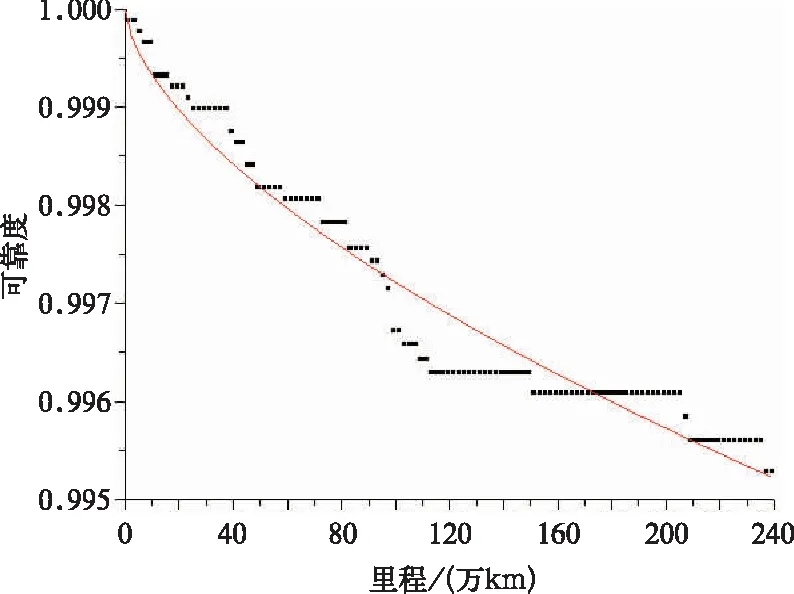
图6 空气弹簧历史累计失效规律
3.2 各参数历史失效度和复杂度计算
基于生存分析法和经验分布拟合,得到各参数对应失效模式的历史累计失效规律,其中以空气弹簧为例如图6所示,进而得到各参数现行维修周期的历史累计失效率以及韦布尔分布参数如表5所示。
同时,统计各参数包含的重要组件数,采用第2.2节中的计算方法,得到各参数的结构复杂度和历史失效度如表6所示。

表5 各参数历史累计失效率

表6 各参数历史失效度和结构复杂度计算结果
3.3 系统可靠度分配

3.4 系统高级修周期优化
对比可靠度分配结果和现行维修周期各零部件的可靠度可以发现,现行维修周期的可靠度均满足分配的可靠度要求,即存在一定的维修周期优化空间。采用第2.4节中考虑高级修周期与旋修周期整数倍关系的维修周期优化方法,研究k不同取值时的维修策略。
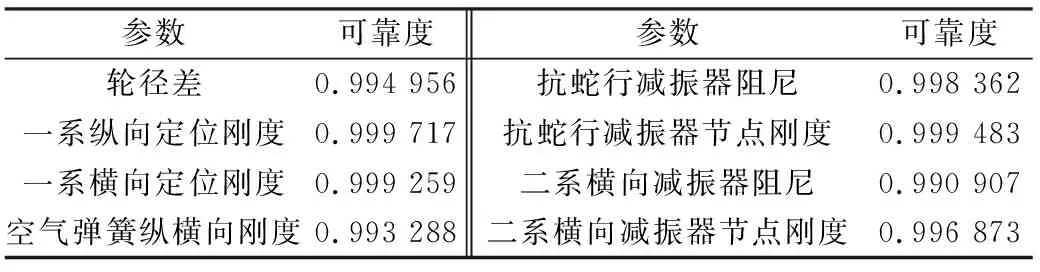
表7 各参数可靠度分配结果
首先研究k不变的情况,即k1=6,此时系统可靠性模型不变,计算得到不同维修周期下系统的可靠度结果见表8。

表8 各维修周期的系统可靠度预计k1=6
可见,选择Ts1=144,tw1=24,k1=6,可满足系统稳定性要求,选择Ts1=150,tw1=25,k1=6,几乎可满足系统稳定性要求,即延长旋修周期至24~25万km,延长三级修周期至144~150万km可以保证CRH380B/BL型高速列车稳定性满足要求。
下面研究k2=7的情况,此时,系统逻辑关系变为7个轮对串联,系统的可靠性模型发生变化,计算得到不同维修周期下系统的可靠度结果为见表9。

表9 各维修周期的系统可靠度预计k2=7
可见,选择Ts2=140,tw2=20,k2=7,可满足系统稳定性要求,选择Ts2=147,tw2=21,k2=7,也可满足系统稳定性要求,即保持旋修周期至20~21万km不变的情况下,延长三级修周期至140~147万km可以保证CRH380B/BL型高速列车稳定性满足要求。
同理,k其他取值的维修策略研究不再赘述。
4 结 论
创新性地将车辆结构、车辆动力学与可靠性理论融合,提出了一套比较完整的高速列车稳定性综合可靠性分析的新思路和新方法,并通过算例验证了方法的有效性。研究成果总结如下:
(1)基于高速列车横向稳定性机理以及系统逻辑结构,考虑了各单元的失效模式、重要程度、结构数量和工作时间,建立了高速列车稳定性系统可靠性分析模型;
(2)提出了基于正交试验与极差分析的单元重要度算法、基于历史累计失效率的历史失效度算法、以及简化的结构复杂度算法;
(3)提出了综合考虑单元重要度、结构复杂度、历史失效度和单元工作时间的改进AGREE可靠度分配算法,并进一步研究了以可靠性为中心的维修周期优化算法,对于高速列车设计、制造以及运用、维修均有一定的借鉴和参考意义。
