纱线卷绕系统恒张力模糊控制策略研究
2018-07-10曹薇
曹薇

摘 要:纱线卷绕系统具有不确定性及时变性、纱线卷绕张力值小的特点,导致纱线卷绕张力波动大,控制精度不高等问题。为此,提出了一种卷绕系统恒张力模糊控制策略,理论推导了系统的控制模型,设计了模糊自适应控制器,并最后进行了仿真与实验。结果表明:模糊自适应PD控制器具有良好的鲁棒性,突发干扰信号下,调节时间大约为15 ms;在目标张力值8 cN时,实际张力测试误差变化范围为-0.2~0.3 cN,误差小,达到了较理想的控制效果。
关键词:卷绕系统;张力控制;模糊控制;PID控制器;纱线
中图分类号:TS103.7;TP29
文献标志码:A
文章编号:1009-265X(2018)02-0080-05
Research on Fuzzy Control Strategy of Constant Tension for Yarn Winding System
CAO Wei
(Department of Automation engineering, Guangdong Technical college of waterResource and Electric Engineering, Guangzhou 510925, China)
Abstract:The yarn winding system has the characteristics of uncertainty, time variation and small tension value, and these lead to large fluctuation of yarn winding tension and low control precision. To this end, this paper presented a fuzzy control strategy of constant tension for the winding system, and theoretically derived the control model of the system. Meanwhile, a fuzzy adaptive controller was designed, and finally simulation and experiment were carried out. The results show that the fuzzy adaptive PD controller has good robustness, and the adjusting time is about 15 ms under sudden interference signal. When the target tension value is 8 cN, the error variation range of the actual tension test error is -0.2~0.3 cN. The error is small, and the ideal control effect is achieved.
Key words:winding system; tension control; fuzzy control; PID controller; yarn
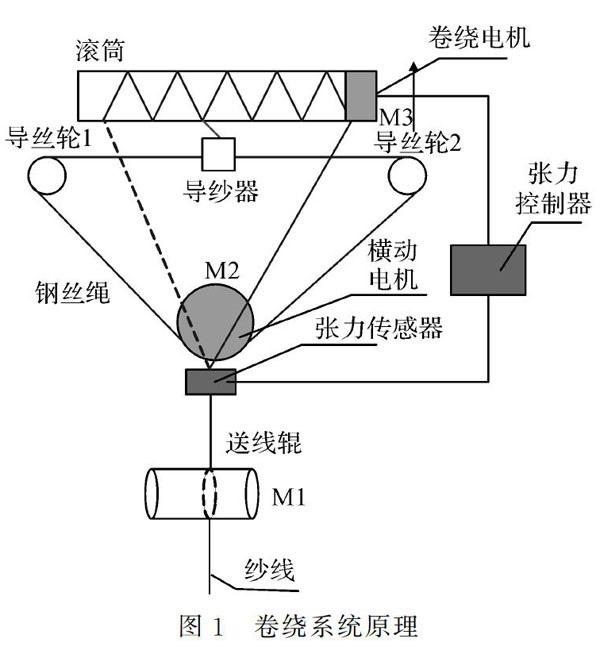
紡纱机的卷绕系统主要由卷绕机构和横动机构组成,横动机构实现导纱器来回摆动排线,卷绕机构实现滚筒连续转动绕线[1-2]。纱线卷绕过程中,其卷绕张力通过卷绕电机速度和横动电机的速度差来控制,张力大小值依靠高精度张力传感器感知,如果卷绕电机速度大于横动电机速度,则纱线被张紧;如果横动电机速度大于卷绕电机速度,则纱线松弛。纱线卷绕张力大小直接关系纱线成品质量,如果卷绕张力过大,则纱线易被挣断,断头率多;反之如果纱线卷绕张力过小,则纱线松弛,容易脱圈,所以纱线卷绕张力最好保持恒定[3-4]。影响纱线卷绕张力的因素主要有两方面:一方面由于纱线卷绕系统的不确定性与时变性,使得传统的张力控制方法难以满足要求,另一方面,由于纱线卷绕本身所需的张力值小,这又对控制精度提出了更高的要求。国内外学者对张力控制问题的解决方法主要还是采用智能算法应用于控制系统中,以达到控制优化的目的[5-8]。为此,本文针对纱线卷绕张力波动大,控制精度不高等问题,提出了一种卷绕系统恒张力模糊控制策略。模糊自适应控制器克服了被控对象模型不精确的缺陷[9-10],以系统的误差及误差变化量为输入,通过模糊推理计算系统的输出量,再通过清晰化计算控制器的PID参数,最后通过叠加得到最终控制器的参数,以达到较理想的控制效果。
1 卷绕系统建模
纺纱机的卷绕系统(图1)主要由卷绕机构和横动机构组成,横动伺服机构主要通过控制横动伺服电机正反转带动钢丝轮正反转,通过钢丝绳传力带动导纱器来回摆动。卷绕机构主要由卷绕伺服电机和滚筒组成,由卷绕伺服电机带动滚筒转动。纱线张力通过卷绕电机速度和横动电机的速度差来控制,其实际张力值通过设置于送纱机构和卷绕机构的张力传感器感知。纱线恒张力控制可转化为:卷绕电机和横动电机之间的合速度控制,通过设置张力值与感知张力值得大小比较来实时调节卷绕电机和横动电机的速度差,保持速度差为恒定值。
假设送纱速度恒定,那么恒张力控制问题最终转化为卷绕伺服电机的速度控制问题。根据电机的拖动方程及横动系统的传动关系可得:
电磁力矩:Te=KT·U=TL+Jedωedt
负载力矩:TL=JLdωLdt+fLωL
电机角速度:ωe=dθedt
负载角速度:ωL=dθLdt
电机转角:θe=N·θL
卷绕张力:F=KF·θL·r(1)
式中:U为电压,KT为比例系数,Je为电机转动惯量,ωe为电机角速度,JL为负载转动惯量,ωL为负载角速度,fL为摩擦系数,N为电机到负载的传动比,F为卷绕张力,r为卷筒半径。
将式(1)方程组内方程合并得到:
1KFJL+Je1KFd2Fdt2+fL1KFdFdt=rKTU(2)
对式(2)两边进行拉普拉斯变换,即可得到卷绕系统的传递函数为:
G(s)=F(s)U(s)=1sJL+JerKTKFs+fLrKFKT(3)
2 模糊自适应PD控制器设计
2.1 张力PD控制器原理
卷绕系统的控制框图如图2所示,系统以设定张力为输入,以电机转速为输出,通过模糊自适应控制器和张力传感器来反馈调节。其中,模糊自适应PD控制器以系统张力误差e和ec为为输入,以比例调节系数的变化量ΔKp和微分调节系数的变化量ΔKd为输出,通过模糊推理的方法来在线调整参数Kp、Kd,然后依靠PD控制器、伺服电机驱动器来控制卷绕伺服电机的转速。
2.2 控制器设计
2.2.1 模糊变量论域隶属度函数
PD模糊控制器为两输入两输出,变量e,ec,ΔKp,ΔKd取值为NB(负大),NM(负中),NS(负小),ZO(零),PS(正小),PM(正中),PN(正大)7个元素,论域范围设定为[-3,3]区间的离散化变量,系统的偏差及偏差变化量e,ec的模糊子集为:
e,ec={NB,NM,NS,ZO,PS,PM,PN}(4)
系统的偏差及偏差变化量e,ec的论域为:
e=[-3,-2,-1,0,1,2,3],ec=[-3,-2,-1,0,1,2,3],比例因子Ke=0.2,Kec=0.4,K1=0.4,K2=0.4。控制系统误差采用的对称三角形隶属度函数如图3所示。
2.2.2 模糊控制规则建立
确定模糊控制规则的基本原则就是减小误差,保证控制器的输出能够使系统响应快、准、狠。ΔKp,ΔKd参数的模糊调整规则如表1所示。
2.2.3 清晰化
采用加权平均法来计算控制器的输出ΔKp,ΔKd,表达式如下:
ΔKp(e,ec)=∑7j=1μj(e,ec)·ΔKpj∑7j=1μj(e,ec)
ΔKd(e,ec)=∑7j=1μj(e,ec)·ΔKdj∑7j=1μj(e,ec)(5)
式中:μj(e,ec)为元素第j级隶属度值,ΔKpj为第j级元素加权系数。
将参变量ΔKp,ΔKd加上上一周期的参数值Kp0,Kd0,即得到参数Kp,Kd的更新公式为:
Kp=Kp0+ΔKp
Kd=Kd0+ΔKd(6)
3 仿真及试验结果分析
通过Matlab/Simulink进行仿真检验模糊自适应控制器的性能,并通过试验平台进行验证。仿真参数设置如表2所示,输入曲线如图4所示,并在300 ms给系统添加一个阶跃干扰信号。PD控制器的参数Kp,Kd变化曲线如图5、图6所示。
由仿真曲线图5、图6可以看出,Kp、Kd经过60 ms的调整趋于稳定,300 ms时,对来自于输入信号的干扰信号,Kp、Kd出现了微小波动,调整时间大约为15 ms,系统解除干扰,恢复稳定,优化后的Kp=1.035、Kd=0.128。且Kp、Kd的变化趋势与输入信号趋同,模糊自适应PD算法具有很好的适应性,控制器能快速趋于稳定,表现出了良好的鲁棒性。
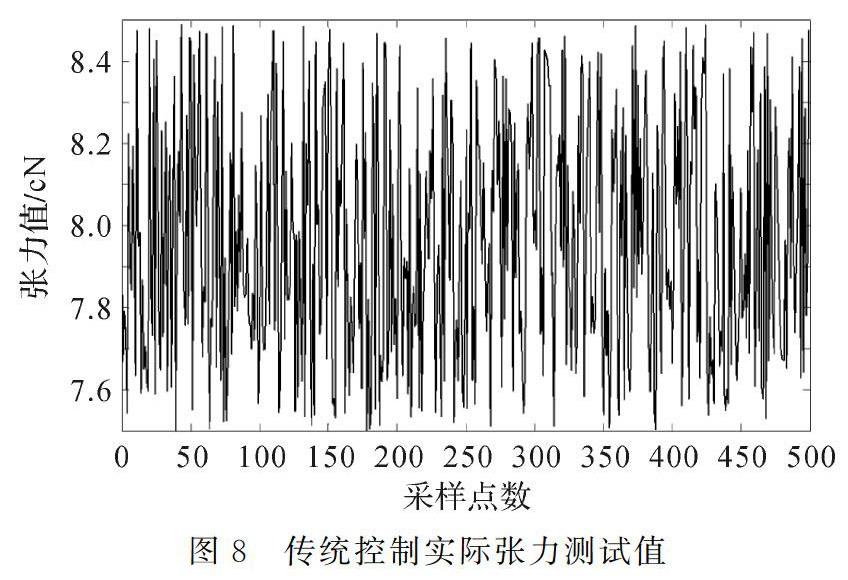
为了进一步验证模糊自适应算法的PD控制器及张力控制系统对恒张力控制的效果,在张力控制试验平台上進行了传统PD控制器和模糊自适应PD控制器的恒张力实测试验,试验平台如图7所示,传统PD控制器控制张力测试值如图8所示。模糊自适应PD控制器的参数设置如表1所示,设置纺纱机卷绕速度为500 m/min,张力值为8 cN,采样周期为0.05 s,该状态下实际张力值如图9所示。
由图8可知,控制张力值为8 cN时,误差在±0.5 cN范围内变化,而图9中,误差变化范围为-0.2~0.3 cN,张力控制更稳定,控制误差更小。
4 结 论
针对纱线卷绕系统恒张力控制问题,主要做了如下两方面工作:a)理论推导了卷绕系统的控制模型,得出了被控对象的传递函数模型,并提出了一种卷绕系统恒张力模糊自适应控制策略。模糊自适应控制器克服了被控对象模型不精确的缺陷,以系统的误差及误差变化量为输入,通过模糊推理计算系统的输出量,再通过清晰化优化控制器的PID参数,最后通过叠加得到最终控制器的参数。b)仿真结果表明了模糊自适应PD控制器具有良好的鲁棒性,突发干扰信号下,调节时间大约为15 ms。试验结果表明了在目标张力值8 cN时,实际张力测量误差变化范围为-0.2~0.3 cN,误差小,达到了较理想的控制效果。
参考文献:
[1] 姜位洪.织机张力控制系统[D].杭州:浙江大学,2005.
[2] 高晓平,刘俊亮,张占新,等.多功能纱线卷绕装置的设计[J].纺织机械,2009,(6):18-19.
[3] 王绍斌,孙卫国,王文郁.络筒张力和速度对纱线质量的影响[J].棉纺织技术,2002(7):35-37.
[4] JIAN W, ZHANG D, CHEN R. Research on the control technique for optimal dispersion winding system[C]// IEEE International Conference, Mechatronics and Automation. IEEE,2005:1351-1356.
[5] 申志强.张力控制数学模型应用研究[J].华中科技大学学报(自然科学版),2007,35(12):65-67.
[6] 付燕辉.基于DSP纱线张力控制系统的研究[D].哈尔滨:哈尔滨理工大学,2013.
[7] 谢正权,王新厚.非接触式纱线卷绕张力动态检测方法的研究[J].中国测试,2009,35(4):111-114.
[8] 谢卫东,王春光,任冬友,等.防止异向纱线重叠的卷绕比动态调节方法[J].纺织学报,2011,32(7):40-43.
[9] 王雁平,马会全.基于模糊算法的收卷机恒张力控制[J].天津工业大学学报,2012,31(4):72-75.
[10] 闫娟,杨慧斌,程武山,等.基于模糊PID的穿丝机张力控制系统设计[J].机械设计与制造,2015(9):174-177.
