一种并联机构天线座的运动学研究
2018-07-10陈腾飞陈陶菲向华平
陈腾飞,陈陶菲,向华平
(南京电子技术研究所, 江苏 南京 210039)
引 言
并联机构于1928年出现,并在20世纪80年代中后期开始成为国际上的研究热点,进入快速发展时期,距今已快速发展30余年,取得了丰硕的研究成果。并联机构已经成功应用于飞行模拟器、模拟对接试验台、空间站异体同构周边式对接机构、工业机器人领域、医用机器人领域、并联机床、微动调节机构、载荷模拟器、稳定平台、振动隔离与精确指向机构、FAST 500 m口径球面射电望远镜等诸多领域[1-3]。
传统并联机构具有刚度大、均化误差、负荷自重比大等[4]优点。如果将并联机构用于天线座,则有以下优点:1)提高天线座的刚度;2)提高阵面的指向精度;3)在大机动环境下驱动天线转动时减轻电机负载;4)与驱动并联相对应的是制动并联,这样可以提高天线座锁紧制动的安全系数。这说明将并联机构用于天线座可以提高天线座的性能,开展这方面的研究工作对其工程应用是有意义的。国内已有相关高校、研究所对并联机构在天线座上的应用展开研究,主要是将Stewart平台用于射电望远镜的阵面调整机构中[2],以及FAST的馈源舱的两级调节机构[3],但针对本文所提出的并联机构的研究还较少。
文中根据一种机载天线座的技术指标,提出一种3UPS-U型的并联机构,计算其自由度、位姿逆解和位姿正解,推导其雅可比矩阵并求解其速度正、逆解。最后基于理论模型,用Matlab进行数值仿真,得到位姿逆解和速度逆解的曲线。
1 自由度分析
3UPS-U型并联机构天线座由固定平台A1A2A3、动平台B1B2B3、3个主动链(A1B1、A2B2、A3B3)和1个从动链OAOB组成。固定平台和动平台都是等边三角形,OA、OB是其几何中心。A1、A2、A3是虎克铰,用U表示。B1、B2、B3是球铰的位置,用S表示。从动链OAOB中的点O是虎克铰。虎克铰和球铰之间是移动副,用P表示,由此组成3UPS-U型并联机构,具体的机构简图见图1。
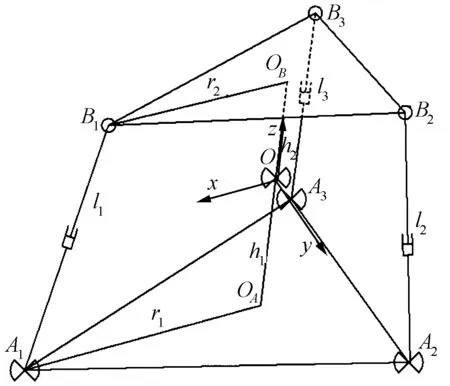
图1 3UPS-U型机构简图
采用Kutzbach-Glübler公式计算此机构的自由度:
(1)
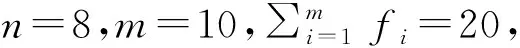
进一步分析此3UPS-U型并联机构天线座的自由度性质。由文献[5]可知,3个主动链对动平台无运动约束,所以此并联机构天线座的自由度数和性质取决于从动链,由于从动链只有一个U副,因此动平台的自由度数和性质与U副相同,即此并联机构天线座具有2个转动自由度,2个转轴与从动链U副的2个转轴重合。
2 机构位姿分析
2.1 机构位姿逆解
求解此并联天线座的机构位姿逆解就是已知动平台的姿态角,求解3个主动链移动副的伸缩位移变化量。为方便求解,需要在图1中建立坐标系。以从动链OAOB的虎克铰位置O为原点建立惯性坐标系O-xyz,其中x轴平行于A1A2A3平面和OAA1直线,z轴垂直于A1A2A3平面,从动链中虎克铰的2个转轴分别与此惯性坐标系的x轴和y轴重合,此坐标系与静平台固连,不随动平台运动而动。为方便推导求解,以O为原点建立随动坐标系O′-x′y′z′,其中x轴平行于B1B2B3平面和OBB1直线,z轴垂直于B1B2B3平面,此坐标系与动平台固连,随动平台转动而转动。
为方便描述动平台的姿态变换,引入Euler姿态角。随动坐标系O1-x1y1z1与惯性坐标系O-xyz重合。先绕y1轴转动θ角到坐标系O2-x2y2z2,再绕x2轴转动φ角到随动坐标系O′-x′y′z′,由此建立惯性坐标系和随动坐标系的映射矩阵:
R=Ry,θRx,φ=
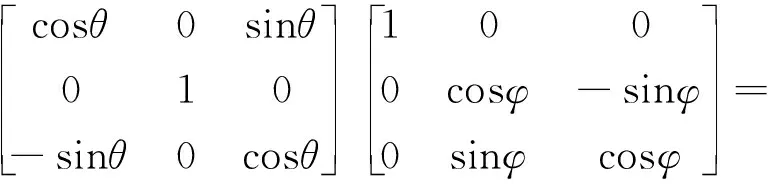
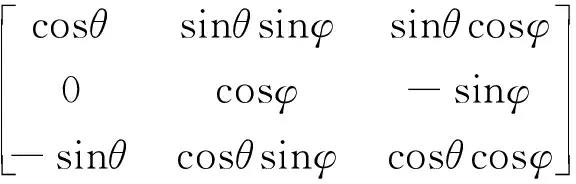
(2)
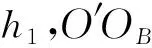
在O-xyz坐标系中,A1、A2、A3三点的坐标:
在O′-x′y′z′坐标系中,B1、B2、B3三点的坐标为:
由式(2)的映射矩阵得到B1、B2、B3三点在O-xyz坐标系的坐标:
(3)
在机构简图中有矢量关系式:
(4)
则天线座在惯性坐标系中任意姿态的主动链长度:
(5)
展开得:
(6)
由此,已知姿态角(θ,φ),可由式(6)求得主动链移动副的伸缩位移变化:
Δli=li-l0
(7)
可见求解并联天线座的机构位姿逆解比较容易。在天线座实际控制系统中,当输入所需姿态角后,系统需要解算出电动缸的伸缩量。并联机构逆解较容易求解,这降低了系统解算的难度,对天线座伺服系统有益。
2.2 机构位姿正解
已知3个主动链移动副的伸缩位移变化量,求解动平台姿态角的过程就是求解机构位姿正解。传统的并联机构比较复杂,根据约束条件,列出求解方程组,但是此方程组高度非线性,参数间相互耦合,因此位姿正解难度较大。如采用数值方法求解此非线性方程组,可以得到近似解。数值解有通用性,但是很难得到全部解。另一种解法是解析法,可以求得全部解,但是对每种类型的并联机构都需要分析推导,而且机构自由度越多,分析推导的规模越庞大,越复杂[5]。由于本并联天线座只有2个自由度,故采用解析法进行求解。
根据式(6)可以得到3个主动链的约束方程:
(xBi-xAi)2+(yBi-yAi)2+(zBi-zAi)2-li2=0
i=1,2,3
(8)
式(8)是关于θ、φ的三角函数高次非线性方程组,用解析法很难消元求解。为避免三角函数的引入,把映射矩阵(2)用方向余弦矩阵来表示:
(9)
一般的方向余弦矩阵共有9个元素,3个元素独立,因此有6个约束方程:
lx2+ly2+lz2=1
(10)
mx2+my2+mz2=1
(11)
lxmx+lymy+lzmz=0
(12)
nx=lymz-lzmy
(13)
ny=lzmx-lxmz
(14)
nz=lxmy-lymx
(15)
由于式(9)和式(2)等效,因此:
ly=0
(16)
把式(9)带入式(8)得到约束方程,此时约束方程的未知数由三角函数替换为式(9)的9个未知数。此3UPS-U型并联天线座有3个主动链,但是动平台只有2个自由度,驱动数大于自由度数,属于冗余驱动机构,因此式(8)的3个约束方程有2个相关,也就是3个约束方程中只有2个是独立的方程。联立式(8)和式(10)~(16),共9个方程,形成九元二次方程组。通过符号推导,可以求得封闭解。
以上文分析为基础,可解得姿态角:
(17)
(18)
3UPS-U型并联天线座机构的位姿正解的求解过程与其他类型的并联机构相比较为简单,这主要是因为静平台和动平台间连接的虎克铰从动链限制了它的自由度,降低了位姿正解的求解难度。这种位姿正解的理论值为后续理论分析打下了基础。
3 机构速度分析
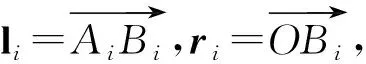
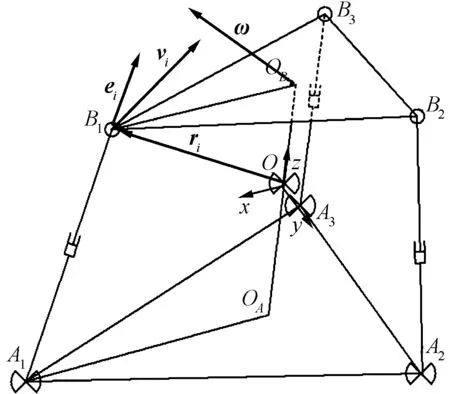
图2 参数矢量图
动平台球铰位置点Bi处的速度:
vi=ω×ri
(19)
移动副线速度是球铰位置点速度在主动链方向的投影:
(20)
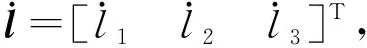
(21)
这就是此3UPS-U型并联天线座的速度逆解,则速度正解:
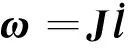
(22)
式(21)是移动副线速度和动平台惯性坐标系角速度之间的映射关系,为方便使用,需要建立绝对角速度和姿态角速度间的映射关系式即(θ,φ)→ω。
动平台在随动坐标系O′-x′y′z′的角速度和姿态角的映射关系式可用Euler运动学方程表述:
(23)
动平台在惯性坐标系O-xyz的角速度:
ω=Rω(O′)
(24)
由此映射关系式建立。
4 数值仿真
本节对2、3节的理论推导进行数值仿真,给出数值算例。对各参数的赋值如下:
静平台A1A2A3的外接圆直径r1=500 mm,动平台B1B2B3的外接圆直径r2=280 mm,中央虎克铰与静平台距离h1=500 mm,中央虎克铰与动平台距离h2=120 mm。为避开机构的奇异位姿,把动平台绕z轴旋转20°作为初始位姿的输入。依照雷达天线的经典转动路径,设动平台的姿态角(θ,φ)从(0,0)到(35°,35°),再回到初始位姿(0,0),共用时2 s。具体的运动规律用参数方程表述为:
用Matlab编程计算得到3个移动副相对于初始位姿的位移曲线,见图3。
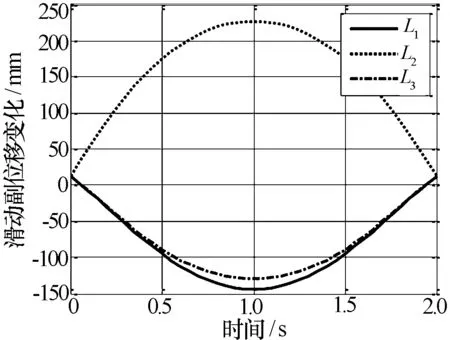
图3 移动副位移曲线
由式(19)~(24)计算得到动平台在惯性坐标系的角速度曲线(图4)和3个移动副的线速度曲线(图5)。
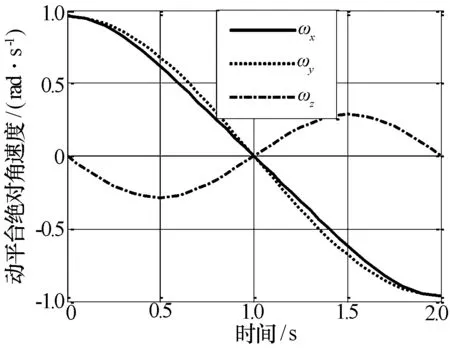
图4 动平台绝对角速度曲线
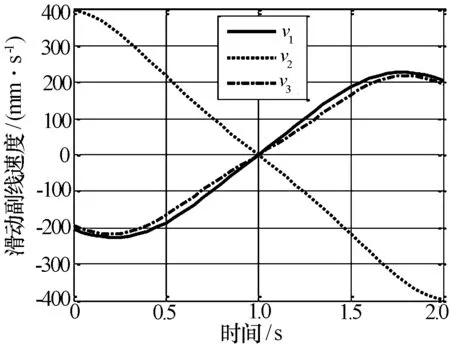
图5 移动副线速度曲线
5 结束语
本文基于并联机构天线座的优势,提出一种3UPS-U型并联天线座。计算出此并联天线座的自由度,分析了位姿逆解和位姿正解。基于运动模型,推导出雅可比矩阵,建立移动副输入线速度和动平台输出角速度间的映射关系。
根据设计尺寸参数,对机构进行运动学数值仿真,得到给定运动轨迹下,移动副的位移曲线和速度曲线。
研究结果表明:该类构型的并联天线座满足天线的机械扫描自由度要求;位姿逆解的易解性对于伺服控制有益;用解析法求解位姿正解可以得到全部解,并且为下一步的理论研究打下基础;中央虎克铰的存在简化了此并联天线座的运动学分析过程,使雅可比矩阵能够以较简洁的方式表述出来;数值仿真分析得到的数据曲线为天线座的机构设计提供借鉴。
本文所做相关分析为更深一步的理论研究如奇异分析、动力学建模、性能分析打下基础,并对工程应用中的机构设计和伺服控制具有重要的参考意义。
参考文献
[1]张新. 一种3-UPS/S球面并联机构的运动参数优化研究[D]. 秦皇岛: 燕山大学, 2013: 1-7.
[2]段艳宾, 贾彦辉, 李建军, 等. 应用于天线座的并联机构构型设计[J]. 机械制造, 2014, 52(600): 26-27.
[3]孙欣. 大射电望远镜悬索式馈源支撑系统的非线性静力学、运动学和动力学理论及方法的研究[D]. 西安: 西安电子科技大学, 2001: 1-4.
[4]刘欣, 仇原鹰, 盛英. 平面冗余驱动并联机器人的性能分析与尺度综合[J]. 电子机械工程, 2010, 26(6): 1-2.
[5]黄真, 赵永生, 赵铁石. 高等空间机构学[M]. 北京: 高等教育出版社, 2006: 1-87, 158, 159.
