以下游释放顺序为导向的汽车总装车间重排序
2018-07-10李延辉
李延辉,孙 辉
(东南大学, 江苏 南京 211189)
引 言
作为“丰田生产系统”的重要部分,平准化排序法(level scheduling)得到了广泛的关注和应用[1]。这种排序方法旨在寻求满足准时制生产方式(JIT)要求的生产序列,使总装车间各工作站上的物料消耗速度尽量保持稳定,以避免物料短缺或库存水平过高。根据不同的目标,平准化排序法又可分为基于零部件的排序法、基于工作负荷的排序法和基于产品的排序法[2]。将产品作为平准化对象,要求不同类型的产品均匀分布于生产序列中,即基于产品的平准化排序。
一个典型的汽车混合流水装配系统包含车身车间、涂装车间和总装车间。不同车间对产品的投产顺序有不同的偏好,如涂装车间希望同色车辆连续排布以减少清洗喷头造成的切换成本[3];而总装车间则希望产品序列有利于实现物料用量平准化[4]。通常来自涂装车间的车辆序列无法满足下游总装车间的生产要求,因此需要主动对来自上游的序列进行调整[5]。在实际生产中,线性缓冲区(selectivity bank)投资成本低而重排序效果好,因而在汽车制造厂被广泛使用。
本文研究如何使用线性缓冲区对来自涂装车间的车辆序列进行重排,以满足总装车间基于产品的平准化排序目标的要求。尽管使用线性缓冲区进行重排序的研究已有不少,但绝大多数研究都集中在涂装车间前的重排序问题上[6]。只有文献[7]在总装车间前进行重排序,目标是最小化各工作站上的总作业负荷超载。所有这些重排序研究都是基于传统的重排序思路。和生产物流方向一致,传统的重排序方法通常先确定上游车辆在缓冲区中的排布方案,再确定如何将缓冲区内的车辆释放至下游[5,8]。
文中提出一种以下游释放顺序为导向的重排序思路,即先确定上游车辆离开缓冲区的释放顺序,然后确定车辆在缓冲区内的排布方式。基于此思路,提出了3种重排序方法,最后通过算例验证了方法的有效性和先进性。
1 汽车总装车间平准化重排序问题
1.1 问题描述
图1所示为一个4车道6车位的线性缓冲区。到达缓冲区的上游车辆按顺序选择车道进入,同时缓冲区另一端不同车道上的车辆被选择释放至下游。这样,车辆经过缓冲区后便可以实现序列重排。

图1 线性缓冲区示意图
已知缓冲区有m条车道,每条车道有f个车位,初始状态为空。考虑来自上游涂装车间的车辆序列,序列长度为T(T=mf),且序列中每辆车的车型已知。每辆车在上游序列中的位置i(i=1,…,T)构成序列π={1,…,T}。定义一个双射函数σ∶{1,…,T}→{1,…,T},表示重排序后车辆i在下游序列中的位置,则重排后对应的车辆位置序列π′={σ(1),…,σ(T)}。若上游车辆序列π={1,2,3},存在函数σ,使得σ(1)=2、σ(2)=3、σ(3)=1,则重排后下游车辆序列为π′={2,3,1}。本文所研究的问题是如何利用缓冲区对上游序列进行调整,使得下游序列对应的平准化排序目标值最小。
1.2 数学模型
数字模型的参数和变量如表1所示。

表1 参数和变量
根据问题描述和表1内的参数和变量,本文所研究的汽车总装车间平准化重排序问题可用以下整数规划模型来表示:
min:
(1)
s.t.:
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
zi,j≤ui,j≤fzi,j,
i=0,…,T-1;j=i+1,…,T
(10)
(11)
i=0, …,T-1;j=i+1, …,T
(12)
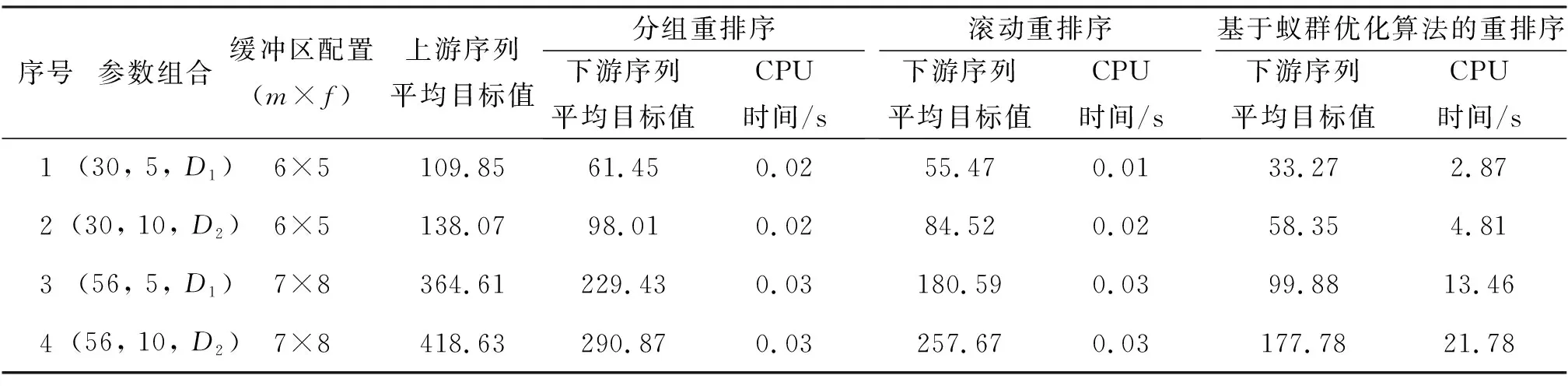
zi,j∈{0,1},i,j=0, …,T;i (13) ek,i∈{0,1},k,i=1, …,T (14) 平准化重排序的目标如式(1)所示,即最小化序列内所有车型实际生产率与理想生产率偏差的总平方和。式(2)~式(14)为约束条件。式(2)和式(3)共同规定了上下游序列车辆之间一一对应的关系。式(4)要求每一辆车停放在一条车道的最前端,或所在车道的前方相邻位置都有一辆上游位置靠前的车。式(5)规定了每辆车后相邻车位最多只能安排给一辆上游位置靠后的车辆停放。式(6)表示车辆所占车道数不得超过缓冲区总车道数。式(7)给出了车辆占用车道数的下界。式(8)和式(9)给出了ui,j的递推关系,使ui,j的值等于车辆i后同一车道内的车辆数。式(10)表示缓冲区每一车道所放置的车辆数不超过车道容量。式(11)表示上游序列所有车辆都被放置在缓冲区中。式(12)表示车辆在进出缓冲区时满足先进先出规则。式(13)和式(14)表示zi,j和ek,i是0-1整数变量。 和平准化排序问题相同,平准化重排序问题也是一个NP难问题。这样,在可接受的时间范围内无法采用精确算法求得大规模算例的最优解,因此考虑采用启发式算法快速近似求解。基于以下游释放顺序为导向的重排序思路,本文提出了3种重排序方法,即分组重排序、滚动重排序和基于蚁群优化算法的重排序。 首先将上游车辆序列分为连续的f个子序列(每个子序列中有m辆车),然后再依次确定每一子序列内所有车辆在下游序列中的位置。由于每组(即每一子序列)的车辆数和车道数相等,因此各组车辆可以依次占据缓冲区中同一列上的所有车位,这样可以保证所有车辆均能按照计划下游序列顺利释放。 在对一个子序列进行重排序时,假设下游序列中已有K辆车,按照以下步骤从该子序列中选择第K+1辆车: 1)计算当前下游序列因加入车辆t(t=1,…,m)而导致的目标函数增量Δt: (K+1)rp)2 (15) 式中:t是车辆在当前子序列中的位置;i是车辆在上游序列中的位置。 2)选取Δt最小的车辆作为第K+1辆车。如果多辆车的Δt值相等,则按等概率原则选择其中一辆。 假设上游车辆序列π={1,…,9},缓冲区容量为3×3。将该序列分成π1={1,2,3}、π2={4,5,6}、π3={7,8,9} 3个子序列。按照分组重排序方法依次对每个子序列进行重排序,得到对应的3个子序列π1′={3,1,2}、π2′={6,4,5}、π3′={8,9,7}。车辆在缓冲区内的排布和下游释放序列如图2所示。图中每辆车的第一个数字表示该辆车的上游序列位置,而括号内的数字为该辆车的下游序列位置。 图2 分组重排序示例 在以上分组重排法中使用滚动计划区间,即成为滚动重排序。该方法采用一个长度为m的滚动计划区间,在每一计划区间内根据式(15)连续选择下游释放车辆,直到紧邻缓冲区的那辆车被选择,然后计划区间向后滚动一个位置。下一轮重排序在新的计划区间内进行,直到所有车辆在下游序列中的位置都得到确定。如图3所示,假设缓冲区有4条车道,当前计划区间内第1和第3辆车分别被确定在下游第2和第1个位置释放,下一计划区间为上游序列第2辆车至第5辆车。 图3 滚动计划区间 为确保所得到的下游理想车辆序列能够实现,采用文献[5]中的堆栈规则确定车辆在缓冲区内的位置:假设下游序列π′={σ(1),…,σ(T)},将满足不等式(l-1)m+1≤σ(i)≤lm的m辆车放置在缓冲区第l列(l=1,…,f)的m个车位上。 蚁群优化算法最初由Dorigo提出,是模拟蚂蚁觅食过程中利用生物信息素与群体中的其他蚂蚁交换信息,从而获取较短觅食路径(即最优或近优解)的优化算法[9]。由于蚁群算法特别适合于组合优化问题如旅行推销商问题和生产计划问题[9-10],本文提出了基于蚁群算法的两阶段重排序方法。第一阶段采用蚁群算法构建一个完整的下游理想序列,第二阶段以下游理想序列为导向,确定上游车辆在缓冲区内的排布方案。 2.3.1蚁群优化算法 下游车辆序列的构建过程可以看作是人工蚂蚁一步步选择所经车辆路径的过程。因此,蚂蚁经过的完整车辆路径就构成了重排序问题的解。算法的基本思路如下:首先是信息素矩阵τ的初始化。τ中的元素τu,v定义在任意两个车型u和v之间,为蚂蚁在构建解的过程中留下的累积信息素浓度,表示在车型u后选择v的倾向程度。初始化时将所有元素设为一个很小的正数τ0,然后通过迭代搜索求解。每次迭代中,种群中的n只蚂蚁先分别随机选出下游序列的第一辆车,然后按照状态转移规则选择后续车辆。这些蚂蚁构建解的过程是并行同步的,即所有蚂蚁都选择一辆车后才能开始下一辆车的选择。另外,所有蚂蚁前进一步后,立刻进行信息素的局部更新。当所有蚂蚁都完成序列构建后,选出本次迭代的最优序列S+,并与至今最优序列S*比较。若S+优于S*,则用S+替换S*。若S+与S*所对应的目标函数值相等,则保存S+作为另一至今最优序列。然后进行信息素的全局更新,完成本次迭代。重复迭代直至达到最大迭代次数tmax。注意,最后得到的最优解序列可能不止一个。 以上所述蚁群优化算法的路径搜索过程总结如下: 初始化信息素矩阵τ,τi,j=τ0 FORt=1 TOtmax FORant=1 TOn 蚂蚁ant随机选择第一辆车 END FOR FORk=2 TO序列长度T FORant=1 TOn 按照状态转移规则选择下游序列第k辆车 END FOR FORant=1 TOn 信息素局部更新 END FOR END FOR FORant=1 TOn 计算蚂蚁构建序列的目标函数值Zant END FOR 计算当前迭代最优序列S+ 更新至今最优序列S* 信息素全局更新 END FOR 输出所有全局最优解 假设当前序列中已有K辆车,最后一辆车型为u,蚂蚁接下来选择上游序列位置为j的车辆(车型为v)的可能性ηu,v,j根据下式计算: (16) 式中:Δj为当前序列中加入第j辆车所引起的目标函数增量,按式(15)计算;α、β、和γ分别表示τu,v、Δj以及j的相对重要性。可以看出,蚂蚁倾向于选择信息素浓度较大且目标函数增量较小的车型。另外,为方便进出缓冲区,上游序列中位置靠前的车辆也被优先选择。 蚂蚁在车辆候选集C(尚未安排下游位置的所有车辆)中根据以下伪随机规则选择下一辆车: (17) 式中:q为[0, 1]间的随机数;q0为[0, 1]间的常数;J表示按照概率pu,v,j选择下一车辆。pu,v,j的计算如下: (18) 在一次迭代中,为避免蚂蚁重复构建相同的序列,当所有蚂蚁前行一步(即选择一辆车)后,每只蚂蚁经过路径的边上的信息素都要按照下式进行局部更新: τu,v=(1-ρ1)τu,v+ρ1τ0 (19) 式中:ρ1表示信息素的蒸发率且0<ρ1<1;τ0为信息素初始值。 在一次迭代完成后,对全局最优路径上的信息素按下式进行全局更新: (20) 式中:ρ2表示信息素的蒸发率且0<ρ2<1;Q为常数;Zant为蚂蚁ant找到的最优路径所对应的目标函数值。 2.3.2确定车辆在缓冲区内位置 基于第一阶段得到的下游理想序列,根据以下规则引导上游车辆依次进入缓冲区: 1)选择非空车道。假设待进入车辆为i,某非空车道最后一辆车为j,i可以进入这条车道的必要条件是σ(i)>σ(j),否则i无法在j之前释放。当有多个备选车道时,选择σ(i)-σ(j)最小的车道。 2)任选一条空车道进入。 如果所有车辆都可按照上述规则选择车道进入,则计划理想序列可以实现,该序列即为最终重排序列。反之,如果某车辆按上述规则无法找到可选车道,则说明理想序列无法顺利实现。如图4所示,下游理想序列π′={3,6,2,5,4,1}。按上述规则,上游前4辆车进入缓冲区后,第5辆车无可选车道。此时可以通过下述交换下游序列位置的方法,对原理想序列进行适当调整,以使所有车辆能够顺利进入缓冲区。 图4 两两交换下游序列位置 假设待进入车辆在上游序列π中位置为i,缓冲区中所有满足σ(i)<σ(j)的车辆j(j∈π)构成待交换车辆的候选集。具体的交换过程如下: 1)两两交换车辆i与候选集内任一车辆(如车辆j)的下游序列位置σ(i)和σ(j),保持其他车辆位置不变,计算交换后序列的目标函数值。按照目标值由小到大的顺序排列待交换车辆,目标值相等的车辆则按照σ(j)由大到小的顺序排列。 2)依次选择候选集中的车辆进行试交换。如果试交换后能够解决当前阻塞问题,则车辆i进入缓冲区。如果所有试交换都不能解决阻塞问题,执行步骤3。 3)选择候选集内第一辆车交换其下游序列位置,然后转至步骤1,重复下一次交换过程,直到车辆i能够顺利进入缓冲区。 图4中上游第5辆车无可选车道,此时第2辆和第4辆车为候选交换车辆。交换车辆5和2后的新序列π′={3,4,2,5,6,1},目标函数值为3.72,而交换车辆5和4之后的新序列π′={3,6,2,4,5,1},目标函数值为2.39,因此选择车辆5和4的交换。可以看出,交换后阻塞问题解决,因此交换有效。此后,当第6辆车进入缓冲区时,所有缓冲区内的车辆构成交换候选集。按照以上交换规则最终选择交换车辆2和6。由于对原下游理想序列进行了微调,最终得到的下游理想序列目标函数值2.39略高于原理想序列目标函数值1.72。 通过设计算例,分析验证以上3种求解算法的性能。在实际生产中,考虑到基础建设成本、库存成本以及运行效率,缓冲区的规模都不会很大,常见的线性缓冲区容量一般为30至100辆车。因此设计大、小两种规模的缓冲区,容量分别为6×5和7×8。上游序列中车型数取5或10。假设不同车型的市场占有率不同,即消费者对不同车型的需求有差异。对于车型数5,每种车型在序列内的累积分布概率D1= {0.3, 0.3, 0.2, 0.1, 0.1}。对于车型数10,每种车型的累积分布概率D2= {0.15, 0.15, 0.15, 0.15, 0.1, 0.1, 0.05, 0.05, 0.05, 0.05}。 考虑(30, 5,D1)、(30, 10,D2)、(56, 5,D1)、(56, 10,D2) 4个参数组合,每个参数组合随机生成10个上游序列,共计40个算例。所有重排序算法程序均基于微软公司的Visual Studio 2013平台采用C++编写,并在一台CPU主频为2.5 GHz,内存为4 GB的个人电脑上运行。使用以上3种重排序方法对所有40个算例进行求解。在使用基于蚁群优化算法的重排序方法时,经过多次试验,选择效果最优的一组参数进行求解:α=1、β=0.1、γ=1、τ0=0.01、q0=0.3、ρ1=ρ2=0.1、Q=0.7、tmax=500。按照不同参数组合计算10个算例的平均目标值和CPU运算时间,见表2。 表2 3种重排序方法的求解结果 将3种重排序方法的结果绘制在图5中。可以看出,在所有参数组合中,3种重排序方法均有效降低了上游序列的目标函数值,且方法一(分组重排序)、方法二(滚动重排序)和方法三(基于蚁群优化算法的重排序)的重排序效果逐渐增强。主要原因可能在于方法三中的下游理想序列是在对上游序列进行整体迭代寻优的基础上得到的。实际上,当上游序列有5种车型时,方法三可以使上游序列的目标值降低约70%;当上游序列有10种车型时,方法三可以有效降低目标值约58%。在求解时间方面,由于采用蚁群迭代优化,方法三的求解时间最长,但相对于实际生产节拍(60 ~ 90 s),该求解时间可以接受。方法一和方法二虽然求解质量稍差,但所需时间少(小于0.1 s)。 图5 3种重排序结果对比 3种重排序方法都有着不错的重排序效果,方法三的重排效果最佳,而方法一和方法二所需求解时间最少。另外,3种重排序方法的重排效果随着车型数的增加而略有下降。 本文针对以下游释放顺序为导向的汽车总装车间平准化重排序问题建立了0-1整数规划模型,并提出了3种求解该问题的重排序方法,即分组重排序、滚动重排序、和基于蚁群优化算法的重排序。算例分析和验证表明,3种重排序法都可有效地对平准化重排序问题进行快速求解,其中基于蚁群优化算法的重排序方法表现最优。 参考文献 [1]KUBIAK W. Minimizing variation of production rates in just-in-time systems: A survey[J]. European Journal of Operational Research, 1993, 66(3): 259-271. [2]BOYSEN N, FLIEDNER M, SCHOLL A. Sequencing mixed-model assembly lines: Survey, classification and model critique[J]. European Journal of Operational Research, 2009, 192(2): 349-373. [3]黄刚. 一类无缓冲区涂装油漆排序问题[J]. 华中科技大学学报: 自然科学版, 2009, 36(7): 108-111. [4]BARD J, SHTUB A, JOSHI S. Sequencing mixed-model assembly lines to level parts usage and minimize line length[J]. International Journal of Production Research, 2006, 32(10): 2431-2454. [5]DING F, SUN H. Sequence alteration and restoration related to sequenced parts delivery on an automobile mixed-model assembly line with multiple departments[J]. International Journal of Production Research, 2004, 42(8): 1525-1543. [6]BOYSEN N, SCHOLL A, WOPPERER N. Resequencing of mixed-model assembly lines: Survey and research agenda[J]. European Journal of Operational Research, 2012, 216(3): 594-604. [7]BOYSEN N, ZENKER M. A decomposition approach for the car resequencing problem with selectivity banks[J]. Computers & Operations Research, 2013, 40(1): 98-108. [8]CHOI W, SHIN H. A real-time sequence control system for the level production of the automobile assembly line[J]. Computers & Industrial Engineering, 1997, 33(3-4): 769-772. [9]DORIGO M,STÜTZLE T. Ant colony optimization[J]. Cambridge: The MIT Press, 2004. [10]姚智骞. 基于蚁群算法的复合材料结构件的返修计划问题[J]. 电子机械工程, 2017, 33(2): 48-55.2 以下游释放顺序为导向的重排序方法
2.1 基于贪婪规则的分组重排序方法
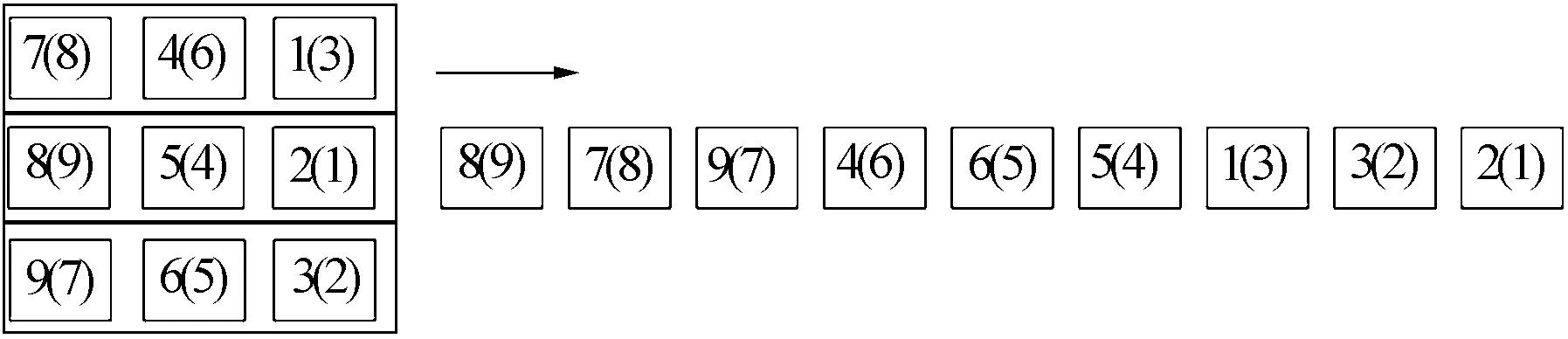
2.2 基于贪婪规则的滚动重排序方法
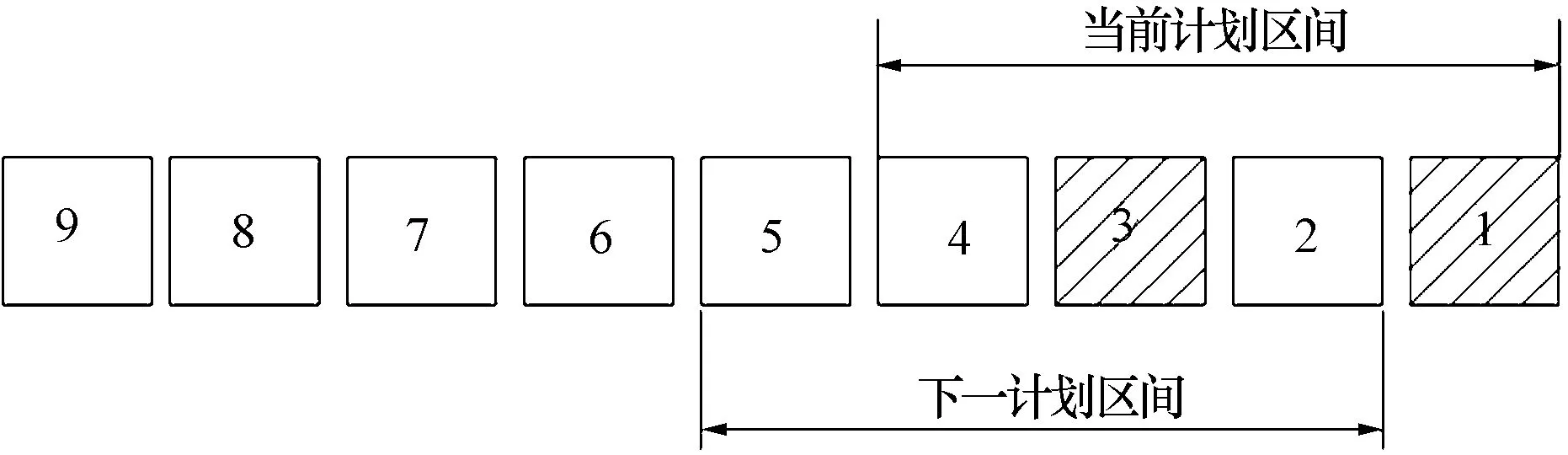
2.3 基于蚁群优化算法的重排序方法

3 算例分析与验证
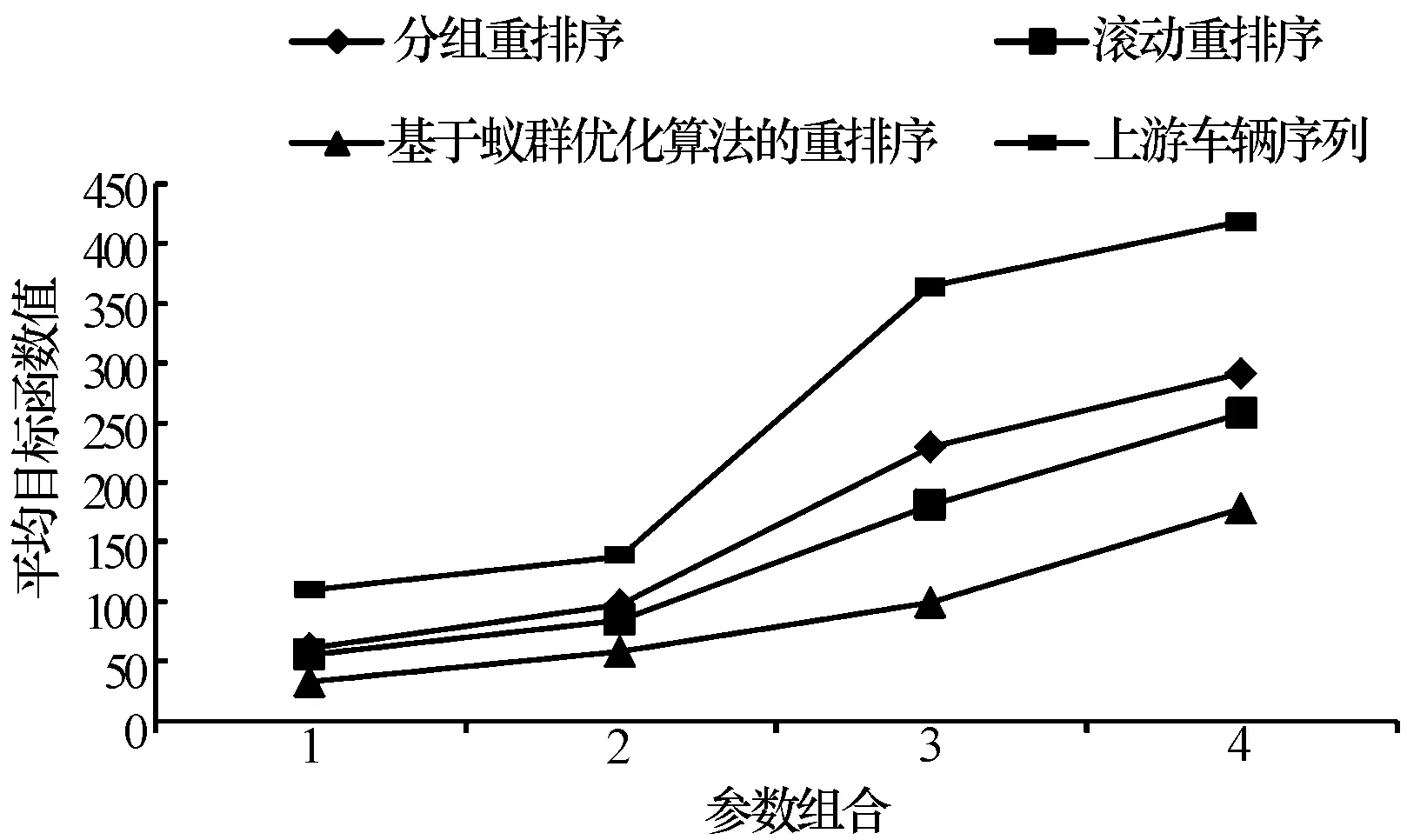
4 结束语
