基于有限差分法和伪谱法的井孔声场数值模拟

吴海燕, 朱祖扬, 张卫

(中国石化石油工程技术研究院, 北京 100101)

0　引　言

在裸眼井地层中,由内到外是流体和井外地层,在套管井地层中,则在流体和井外地层中间还有一层套管,因此井孔地层可以看成径向上是分层的、轴向上是均匀的介质。根据井孔地层的结构特点,优化数值模拟方法,可以高效获取井孔地层中的声波场响应。

声波场的数值模拟方法主要包括有限差分法、有限元法和伪谱法[1-2]。其中,有限差分法实现简单、运算速度快,对于非均匀介质计算具有优势,但是对空间采样和时间采样精度要求较高;有限元法可以灵活地剖分网格,适宜处理具有起伏边界条件和复杂构造的介质模型,但是,低阶有限元会产生频散现象,而高阶有限元则会产生虚假波现象,并且该方法计算量很大;伪谱法基于快速傅里叶变换求解空间导数,其计算精度较高,消耗内存较小,但是不能很好地处理边界以及介质内部物性差异较大的问题[3]。许多学者把上述方法进行结合,以便进一步提高运算效率。林伟军等[4]利用基于有限差分法和离散波数法的2.5维有限差分法计算了轴对称和非轴对称的井孔声场问题;王秀明等[5]利用基于有限元法和谱方法的谱元法计算了弹性波场,严珍珍等[6]利用谱元法模拟了汶川大地震波场传播;马德堂等[7-8]基于有限差分法和伪谱法的混合方法,对起伏介质模型进行了弹性波数值模拟;Furumura等[9]用混合法模拟了1999年中国台湾集集地震波传播,魏星等[10]讨论了混合法在天然地震波场的应用。

基于有限差分法和伪谱法构造的混合方法,适合处理分层介质模型,在进行波场数值模拟时,既提高了运算速度,又保证了数值求解精度,同时节约了计算机的内存空间。本文把该方法应用于井孔声场模拟中,从网格剖分、界面处理等方面验证了该方法的可行性,并对裸眼井声场进行了数值模拟研究。

1　计算方法原理

在笛卡尔坐标系下,定义1个x—z平面的二维均匀弹性介质模型,介质密度为ρ,拉梅系数为λ、μ,则介质的速度和应力的一阶偏微分方程组可以表示为

(1)

(2)

(3)

(4)

(5)

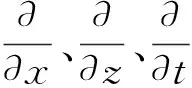
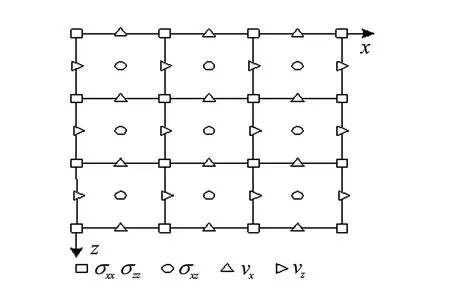
图1　交错网格示意图

(1) 有限差分法。对偏微分方程组(1)～(5)用交错网格有限差分来近似,图1是交错网格示意图。声场中的各个分量按离散的空间和时间点定义,用符号Dx、Dz表示x、z方向的差分算子;am为差分系数;dx、dz为x、z方向的空间步长;Nx、Nz为x、z方向的网格数。则速度和应力的一阶空间导数写作如下,其他分量的空间导数可以做同样的差分表示。

(6)

(7)

(2) 伪谱法。Dx、Dz差分算子也可以用空间傅里叶变换替代,即把空间域求导问题转化为波数域代数乘积问题,这种对偏导数的求解方式称为伪谱法计算。以σxx和vz为例,伪谱法计算的速度和应力一阶空间导数为

(8)

(9)

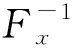
(3) 混合算法。如果对x、z方向的空间导数采用不同的计算方式,则这种计算方式便为混合算法。混合算法融合了有限差分法和伪谱法的优点,对于分层介质模型具有很好的使用效果。采用混合算法技术,在x方向使用伪谱法,在z方向使用有限差分法,方程(1)～(5)改写为

(10)

(11)

(12)

(13)

(14)

2　计算方法验证

为了验证混合算法的可靠性,计算了x—z平面内0.512 m×0.512 m的地层模型。在z方向包含2层介质,分界面位于z=0.212 m处,上层介质是泥岩地层,下层介质是灰岩地层,地层参数见表1。分别采用了上述3种计算方法进行了声场模拟,声源为一阶导数高斯源,函数表达式为s(t)=(t-t0)e-[α(t-t0)]2,t0为波形的中心时间,α=(2πf0)2/2,f0为声源主频。该模型被划分为256×256个网格,x、z方向的空间步长均为0.002 m,时间步长为0.1 μs。声源布置在(0.256 m,0.256 m)位置处,声源频率为100 kHz,在分界面(0.3 m,0.212 m)处放置了1个接收器。

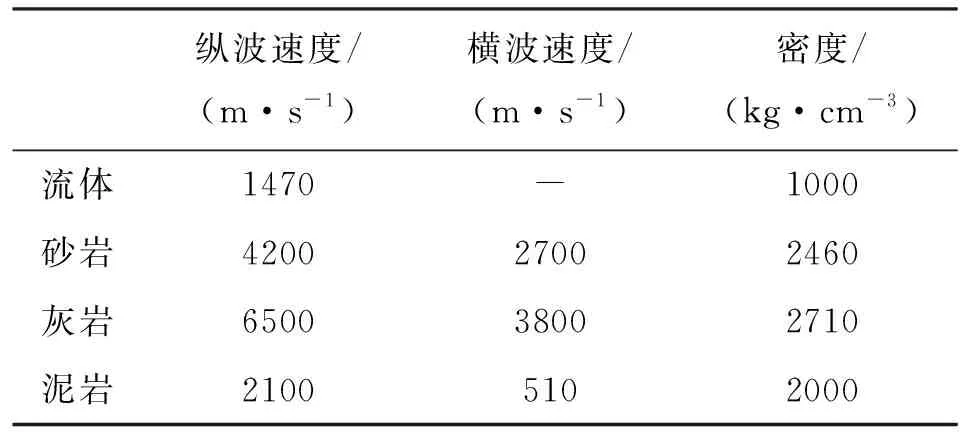
表1　模型参数

图2给出了0.04 ms时刻的x方向速度分量声场快照图,图2(a)、(b)、(c)分别是有限差分法、伪谱法和混合算法计算的结果。可见,当声场传播到地层分界面时,会发生反射和透射现象,上下界面地层均存在纵波和横波,其中下界面地层声速要快于上界面地层声速。有限差分法计算的声场在分界面处空间频散小,分辨率高;而伪谱法计算的声场在分界面处空间频散严重,并且在z方向出现虚假波,这是由于介质突变引起的,而在非分层方向则具有相当的计算精度;混合算法在x方向采用了伪谱法计算声场,而在z方向采用了有限差分法计算声场,声场在分界面空间频散小,有相当的计算精度。图3为分界面处接收器接收到的声波波形,进一步证明了在分界面处,有限差分法(FD)计算的波形“纯净”,而伪谱法(PS)计算的波形存在较长的“拖尾”现象,混合算法(HY)计算的波形和有限差分计算的波形基本一致。因此,混合算法计算结果可靠,处理分层介质声场时具有相当的精度,同时又发挥了伪谱法需要计算机内存资源少的优势。

图2　分层介质模型x方向速度分量声场快照图

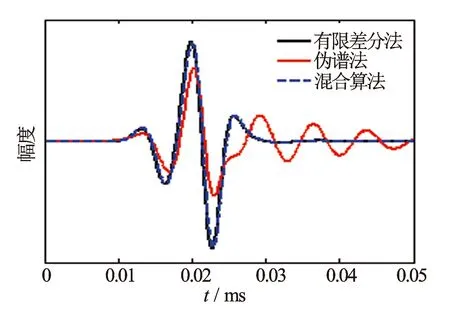
图3　位于分界面处接收器接收到的波形

3　井孔声场模拟

竖直井孔是一种径向分层地层,整个井孔关于井轴(z轴)对称,沿井轴方向井孔和地层参数均不变,沿径向(r轴)是流体和井外地层。井孔模型如图4所示,井轴z左右两侧对称,其中①为井内流体,②为井外地层,在进行模拟计算时,只对井轴z的右侧部分进行计算。针对井孔声场问题,需要把方程(1)～(5)、方程(10)～(14)改为二维柱坐标系下的方程,可以参考文献[11],在z方向使用伪谱法,在r方向使用有限差分法。

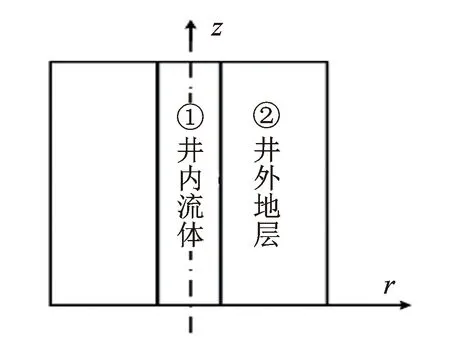
图4　井孔模型

利用混合算法模拟了井孔中的声场传播,模型参数见表1。井外地层为砂岩,井孔半径为0.1 m,计算区域径向长度为3 m,轴向高度为10.24 m。整个计算区域被划分为300×1 024个网格,r和z方向空间步长为0.01 m,时间步长为0.5 μs。在井轴上布置了1个声源和5个接收器,最短源距为0.3 m,接收器间距为0.2 m,使用的声源为一阶导数高斯源,频率为10 kHz。图5显示了0.2、0.4、0.6 ms和0.8 ms时刻的x方向速度声场快照图,由图5可以清晰地看出,声场由井孔内向井外有规律地传播,在井壁处声场发生反射和透射现象,井孔内声场的能量要明显强于井外地层声场的能量。

考察井孔半径对声场传播的影响,把井孔半径增大为0.2 m,其他参数不变。图6为接收器接收到的x方向速度波形,其中实线是井孔半径为0.1 m时的波形,虚线是井孔半径为0.2 m时的波形。由图6可知井孔半径较小时,井内接收到的波形清晰,可以得到井外地层纵波、横波和斯通利波等振型。而当井孔半径较大时,接收器接收到的是随着时间推移在井孔内来回反射的声波,且越到后面波形幅度越小,这不是地层的声波信号。因为声源离井壁较远,声源和接收器的距离小,声波传播在井壁处不满足临界折射条件所致。

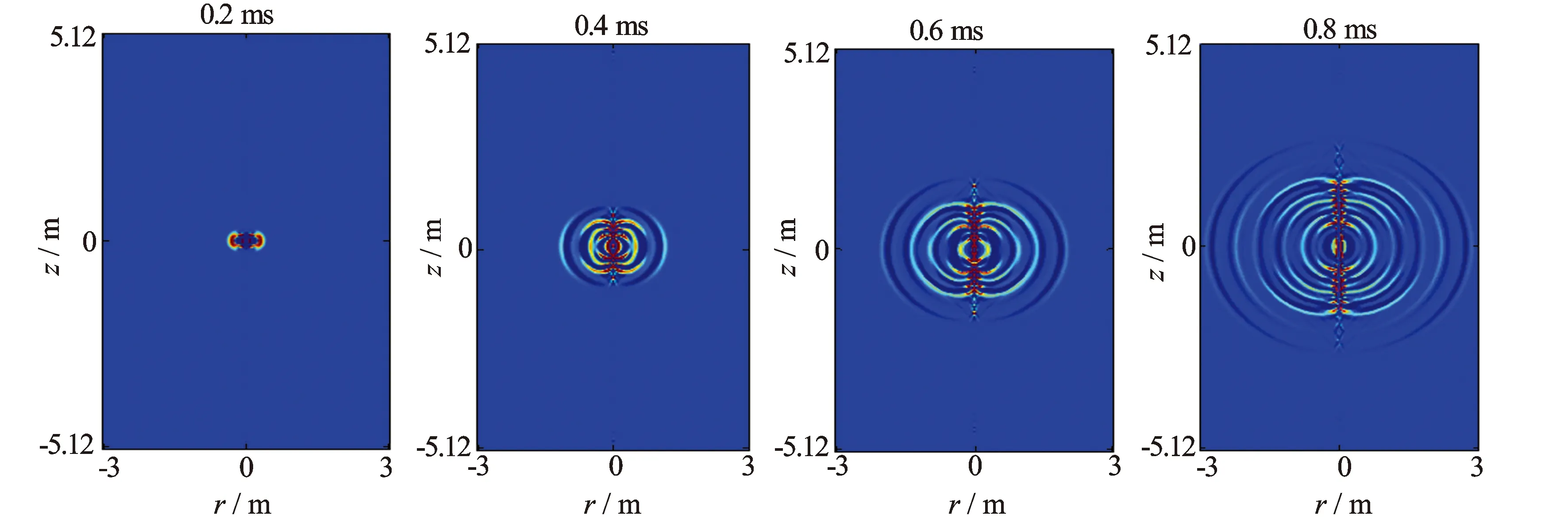
图5　砂岩地层井孔(x方向速度)声场快照图

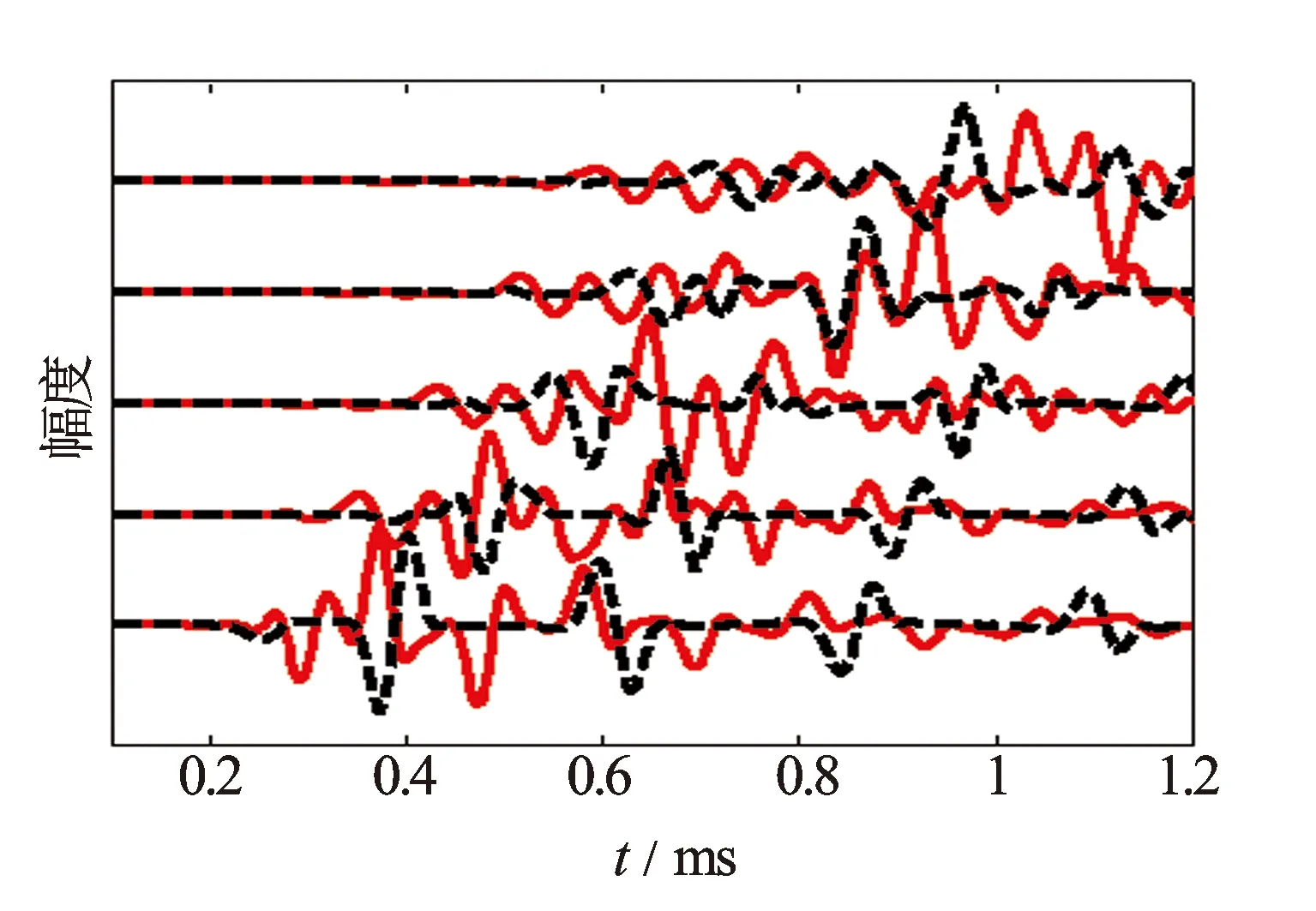
图6　不同井径井孔的声场波形(实线r=0.1 m,虚线r=0.2 m)

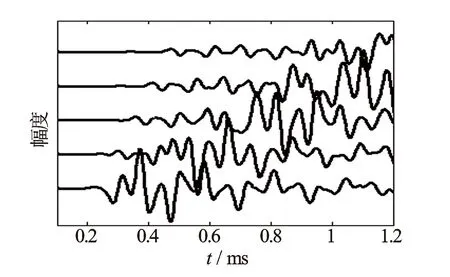
图7　灰岩地层井孔声场波形

进一步考察井外地层对声场传播的影响。井外地层改为灰岩,其他参数不变。图7为接收器接收到的x方向速度波形。与图6相比较,灰岩地层纵波到达时间明显要快于砂岩地层的纵波到达时间,后续到达的横波和斯通利波幅度明显较大,这是因为灰岩地层是一种超硬地层。把井外地层改为泥岩,其他参数不变。图8为接收器接收到的x方向速度波形。与图6相比较,接收器接收到的波形只有纵波和斯通利波,并且泥岩地层纵波到达时间明显要慢于砂岩地层的纵波到达时间,斯通利波幅度也小于砂岩地层的斯通利波幅度,这是因为泥岩地层是一种软地层,由于在井壁处横波传播不满足临界折射条件,因此接收器接收不到横波。

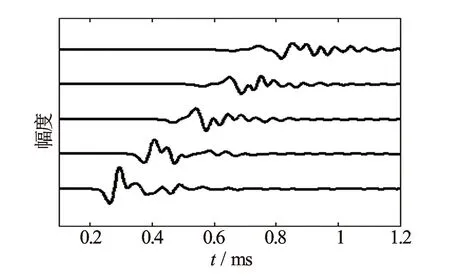
图8　泥岩地层井孔声场波形

4　结　论

(1) 混合算法融合了有限差分法和伪谱法的计算特点,适合处理分层介质地层模型。将混合算法和其他2种方法进行了对比,验证了它的计算结果可靠,在分层介质地层声场模拟时,具有相当的计算精度,同时需要的计算机内存资源较少。

(2) 运用混合算法模拟了井孔声场的传播。在井壁处声场会发生反射和透射现象,井孔内声场的能量要明显强于井外地层声场的能量;当井孔半径较大,接收器与声源的距离较近时,接收器接收不到地层的声波信号;当井外地层分别是砂岩、灰岩和泥岩3种地层时,接收器能测量到砂岩和灰岩地层的纵波、横波和斯通利波信息,而不能测量到泥岩地层的横波信息。

(3) 对于更大范围内的井孔声场模拟,混合算法可以使用并行机来完成大数据量的计算,因此仍具有很好的适用性。井孔声场的模拟结果,可以为声波测井仪器的研制和数据分析提供理论指导。