径向渐变地层阵列侧向电阻率测井响应研究

2018-07-10程文娟许月晨贺飞姜黎明刘凯唐章宏

测井技术 2018年3期

程文娟, 许月晨, 贺飞, 姜黎明, 刘凯, 唐章宏

(1.北京工业大学, 北京 100124; 2.中国石油集团测井有限公司, 陕西西安 710021)

0　引　言

目前,在计算电阻率测井响应时,对侵入影响的分析和校正通常基于泥浆侵入的阶跃模型[1-2]。该模型认为泥浆滤液只侵入地层一段距离,侵入带电阻率恒定,侵入带以外为原状地层,电阻率的这种变化不符合实际地层的变化情况。S形增长模型——Logistic模型[3-4]主要用来描述增长情况,因此,只能模拟侵入带电阻率低于原状地层电阻率(低侵)的情况。本文针对Logistic函数进行改进,提出了改进的三参数Logistic函数描述过渡带电阻率,该函数能很好地描述高侵入与低侵入情况下过渡带电阻率连续变化。

1　渐近变化地层模型构造

地层二维模型见图1。由于泥浆侵入会导致地层电阻率发生变化,根据冲洗带电阻率与原状地层电阻率的差异,将泥浆侵入分为低侵和高侵。为了描述地层电阻率低侵及高侵的渐近变化过程,构造电阻率与侵入深度的渐变模型。

图1　含侵入带的地层二维模型

图2　三参数Logistic函数电阻率随侵入深度的变化曲线

地层电阻率与径向侵入深度的关系可用Logistic模型描述[3-4]。Logistic模型的表达式为

(1)

(2)

式中,Rxo为冲洗带电阻率;Rt为地层真电阻率;r0为井眼半径。由式(1)、式(2)可以看出,R(r0)=Rxo,R(+∞)=Rt。对于低侵地层,RxoRt,此时a<0,函数不存在拐点,因此不能描述高侵时地层电阻率随侵入深度的渐变行为。

针对上述Logistic函数不能描述高侵时地层电阻率随侵入深度的渐变行为的不足,本文提出改进的三参数Logistic函数

(3)

并定义此时径向渐变地层的侵入深度为电阻率变化最大位置(函数拐点位置)

(4)

式中,Rxo为冲洗带电阻率;Rt为地层真电阻率;r0为井眼半径;函数拐点位置为ri=r0-lnk2/b,k2为接近0的常数,例如取k2=0.05。由式(3)、式(4)可以看出,R(r0)=Rxo,R(+∞)=Rt,且函数式(3)能描述地层电阻率不随径向渐变的行为,此时,取c=Rxo=Rt即可。

以上三参数Logistic函数能很好地描述高侵与低侵情况下过渡带电阻率连续变化,且其平稳区的变化可通过调节拐点位置来改变。例如,对于低侵,设r0=0.101 6 m,Rxo=10 Ω·m,Rt=200 Ω·m,可绘制三参数Logistic函数描述的电阻率随侵入深度的曲线变化情况[见图2(a)]。对于高侵,设r0=0.101 6 m,Rxo=20 Ω·m,Rt=5 Ω·m,同样可绘制三参数Logistic函数描述电阻率随侵入深度的曲线变化情况[见图2(b)]。

从图2可知,三参数Logistic函数能很好地描述高侵与低侵情况下过渡带电阻率的连续变化。以下采用三参数Logistic函数描述地层电阻率的渐近变化。

2　径向渐变地层的数值模式匹配法

对于井眼及地层轴对称的结构,利用二维数值模式匹配法(Numerical Mode Matching,NMM法)[5-7]对径向渐变地层模型进行数值模拟。现有的NMM法中认为地层电导率分段均匀,在计算每个区间n的积分过程中不考虑地层电导率随侵入深度的变化,第m层地层第n区间的A、B、G、H矩阵可以表示为

(5)

(6)

(7)

(8)

实际情况下,泥浆侵入会导致地层物性参数径向分布不均匀,因此对于径向渐变地层,构造渐变地层模型,认为地层电导率随侵入深度渐近变化,提出针对径向渐变地层的快速正演计算。此时,NMM法中式(5)所示的第m层地层第n区间A矩阵变为

(9)

B、G、H矩阵与之类似。由于引入Logistic函数描述的径向渐变电阻率,以上矩阵中元素不能通过求积分原函数的解析表达式求解,因此采用Gauss-Legendre公式[8]进行计算

(10)

式中,tk是gauss点;Ak为Gauss-Legendre求积系数;j是高斯点数。

3　计算结果与分析

本文采用阵列侧向(HAL)测井仪器[9-10]进行计算。该测井仪器通过控制不同的电极等电位使得仪器有不同的探测深度,根据探测深度不同有6种不同的探测模式RLA0至RLA5,其探测深度由浅到深,工作原理见文献[9]。

3.1　阶跃地层与径向渐变地层视电阻率差异分析

为研究HAL仪器在阶跃地层与径向渐变地层测量视电阻率的差异,分别构造具有相同冲洗带电阻率、原状地层电阻率和侵入带半径的阶跃模型与径向渐变模型,计算HAL仪器在这2种地层模型的视电阻率。构造的阶跃地层与径向渐变地层低侵模型见图3。图3中,冲洗带电阻率为5 Ω·m,原状地层电阻率为200 Ω·m。同理,构造阶跃地层与径向渐变地层的高侵模型,冲洗带电阻率为20 Ω·m,原状地层电阻率为5 Ω·m。分别计算高侵和低侵地层不同侵入深度下探测模式RLA0至RLA5的视电阻率,并计算阶跃模型与径向渐变模型视电阻率的差异(以阶跃模型计算的视电阻率为标准值,计算径向渐变模型与阶跃模型的视电阻率相对误差)。低侵时2种地层的视电阻率相对误差随侵入深度的变化曲线见图4,高侵时2种地层的视电阻率相对误差随侵入深度的变化曲线见图5。

图3　纵向均匀地层的阶跃模型和径向渐变模型

图4　　低侵时2种模型视电阻率的相对误差随侵入深度的变化曲线

从图4可知,相对误差随侵入深度的变化总体均呈现先增大后减小的趋势。当侵入深度等于井径时(即地层为均匀地层),6条曲线基本重合,且误差基本为0,这也间接说明均匀地层2种计算方法结果一致。从图4中可以看出,RLA0的相对误差曲线在侵入深度较小时变化较大,随着侵入深度的增加很快下降为0,这是由于此时主电极发射的电流不聚焦,很快返回到临近的电极,大部分电流在钻井液内流动,不流经地层,主要探测的是井眼及附近很近的区域。因此,地层侵入深度的变化对RLA0的测井响应影响很小。当侵入深度小于2 m时,侵入深度对RLA1至RLA5相对误差的影响较大,这是由于RLA1至RLA5主电极发射电流,屏蔽电极发射屏蔽电流,且屏蔽电极和控制等电位的电极依次向主电极两边扩展,因此电流在流出后流经的地层越来越深,探测深度依次增加。当探测深度较小时,返回到测量电极的电流主要流经冲洗带,所测的视电阻率主要是受冲洗带电阻率影响。当探测深度较大时,电流流经地层较深的位置然后返回测量电极,所测的视电阻率受原状地层电阻率的影响较大,当冲洗带电阻率和原状地层电阻率的差别一定时,最大相对误差值随着探测深度增大而逐渐减小。从图4中还可以看出,RLA1至RLA5相对误差最大对应的侵入深度是依次增大的,这体现在探测模式RLA1至RLA5的探测深度是递增的。当侵入深度增大到一定程度时,所有探测模式下的相对误差均趋于稳定,且相对误差非常小(基本为0),这是由于当侵入深度较大时,所有探测深度都达不到地层的侵入深度。整体上,针对阶跃地层和Logistic函数描述的径向渐变地层模型,HAL仪器测量的视电阻率差异较大,尤其在仪器探测深度附近。由于实际泥浆侵入后地层电阻率为径向渐近变化,且其侵入深度也基本不超过仪器探测深度,因此,对于低侵模型,有必要在研究HAL仪器测井响应时,模拟实际泥浆侵入后地层电阻率的径向渐变行为。

图5　高侵时视电阻率的相对误差随侵入深度的变化曲线

从图5可知,在靠近井眼的侵入深度下,相对误差随侵入深度变化呈乱序,在部分位置有突变,当侵入深度大于0.14 m之后,相对误差总体均呈现先增大后减小的趋势。然而,对于高侵地层,所有探测深度下径向渐变与分段均匀地层的相对误差值均在4%以下,与低侵情况相比2种地层模型的相对误差很小。

3.2　对比度对视电阻率差异的影响

为进一步研究不同侵入带和原状地层电阻率下2种地层模型视电阻率的差异,设置不同对比度,构造不同地层,分别采用分段均匀地层模型和径向渐变地层模型进行计算,由此得各探测深度下2种模型相对误差最大值随目的层电阻率对比度的变化曲线(见图6)。

图6　2种模型相对误差最大值随目的层电阻率对比度的变化曲线

从图6可知,径向渐变和分段均匀地层视电阻率的相对误差最大值随着目的层电阻率对比度的增大而减小,当对比度小于1时,地层为低侵,2种模型视电阻率差异很大,当对比度大于1时,地层为高侵,视电阻率差异均小于6%。

3.3　带围岩地层结果分析

以上分析径向渐变和分段均匀地层视电阻率差异时,均认为地层纵向均匀,而实际地层纵向分层,因此有必要考虑存在围岩时二者的差异。以下分别构造带围岩的低侵和高侵模型进行分析。

(1) 低侵模型:Rxo=5 Ω·m,Rt=200 Ω·m,侵入深度为0.76 m,上下围岩电阻率为5 Ω·m,目的层厚度4 m,径向渐变和分段均匀地层的测井响应曲线分别见图7(a)、图7(b)。

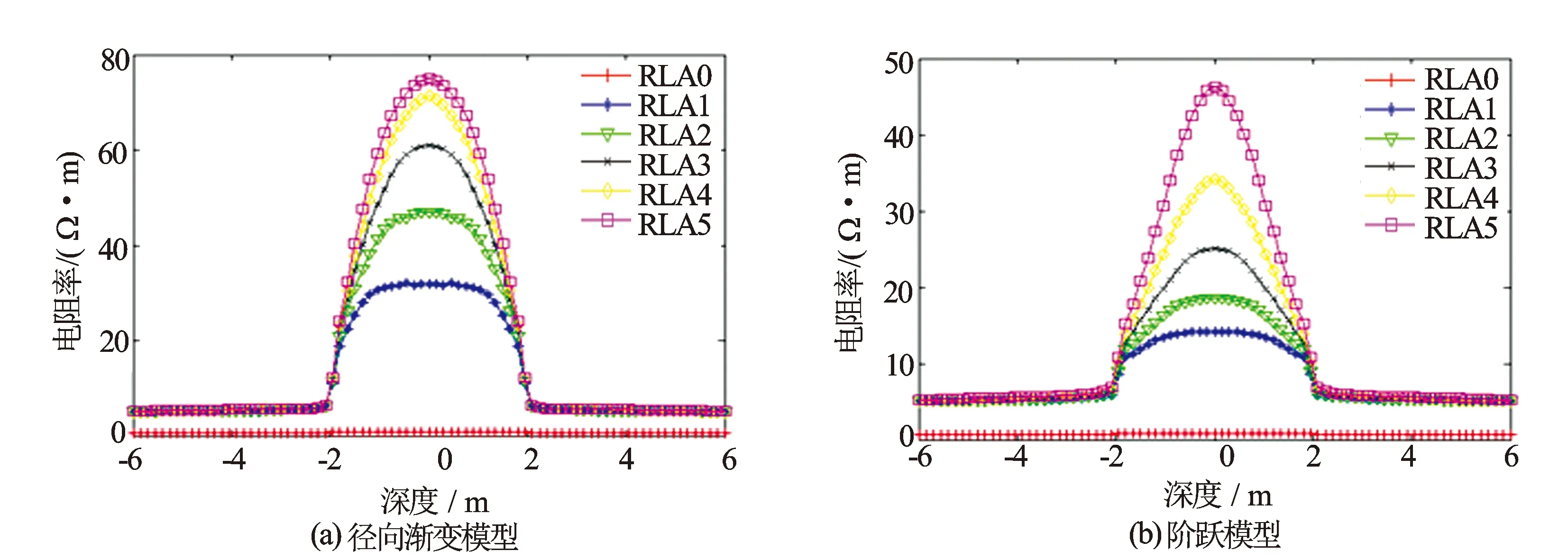
图7　低侵模型的测井响应

(2) 高侵模型:Rxo=20 Ω·m,Rt=5 Ω·m,侵入深度为0.5 m,上下围岩电阻率为5 Ω·m,目的层厚度4 m,径向渐变和分段均匀地层的测井响应曲线分别见图8(a)、图8(b)。

图8　高侵模型的测井响应

从图7可知,对于低侵模型,径向渐变地层的目的层视电阻率值普遍高于阶跃地层目的层视电阻率,这是由于径向渐变地层的电阻率在还没达到侵入深度时已经逐渐增大,导致不同探测模式受低电阻率侵入影响变小。对于带围岩的低侵模型,在研究HAL仪器测井响应时,HAL仪器测量的视电阻率差异较大,因此,也要构造渐变地层模型模拟实际泥浆侵入后地层电阻率的径向渐变行为。