基于MEMS陀螺仪和加速度计的自适应姿态测量算法

盛娟红，张志安，邢炳楠

(南京理工大学 机械工程学院，江苏 南京 210094)

0　引　言

随着低成本惯性器件传感器技术的逐渐成熟，利用MEMS陀螺仪和加速度计进行姿态测量成为近年来捷联式低成本、全固态测量系统的研究热点之一[1-3]. 它具有体积小、成本低、重量轻、能耗低、可靠性高等优点，在各个领域都有广泛的应用[4，5].

由于器件的硬件精度问题，陀螺仪本身存在漂移误差，且易受振动、温度等外部环境因素干扰，导致漂移误差逐渐累积变大，因此，单一的MEMS陀螺仪传感器无法保证长时间测姿的准确性[6]. 文献[7] 采用的是多传感器进行加权平均的融合算法来保证算法可适应动态环境,但是测量精度有待提高； 文献[8]通过建立多传感器误差数据模型比较准确地预测飞行体的姿态，但是却不能适应动态飞行环境. 本文设计了一种基于MEMS陀螺仪和加速度计的自适应姿态测量算法在线实时估计运动体的姿态角度. 算法基于扩展卡尔曼滤波算法来实现数据融合，利用带遗传因子的限定记忆长度的Allan方差在线估计运动时传感器数据误差的量测噪声，实时修正角度估计误差，从而有效解决了动态噪声和姿态最优估计的问题.

1　姿态的运动学模型

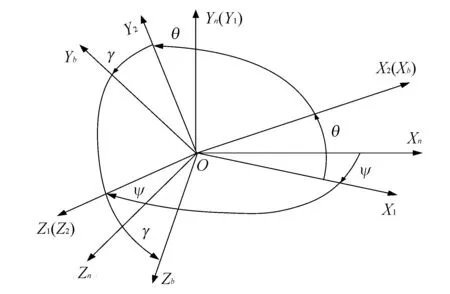
图 1　导航坐标系Fig.1　Navigation coordinate system

本文采用弹道方程中的基准坐标系为导航坐标系，如图 1 所示. 其中OX轴沿水平线指向射击方向，OY轴铅直向上，OZ轴按右手法则确定，垂直于射击面指向右方.

运动体的空间位置可看做依次绕y轴做航向、绕z轴做俯仰、绕x轴做横滚的复合运动，因此，有

(1)

从而推出

(2)

其中

角标n,b分别代表导航坐标系、由运动体确定的动坐标系；Wx,Wy,Wz指陀螺仪输出的3个角速度.

2　自适应扩展Kalman滤波算法

2.1　扩展Kalman滤波器

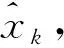
(3)

其中，Wk=[WγWψWθ]T是状态噪声序列； [WxWyWz]T是陀螺输出的角速率. 同时，得到状态方程的雅克比矩阵为

(4)

其中，a11,a13,a21,a23,a31为

利用重力场测量姿态倾角时，把三轴加速度计测得的线加速度值转化成姿态角度信息，以此作为量测值，量测噪声为Vk. 其中，根据量测值和状态值可知Hk为3×3的单位矩阵，此处忽略不写，写出量测方程为

(5)

由于航向角ψ的方向与重力场方向正交，此处加速度计不能用来预测估计航向角度值. 其他两个角为

(6)

根据状态方程与量测方程可以得到预测(时间更新)与量测更新方程，即

预测(时间更新)方程为

(7)

量测更新方程为

Px,k=I-KkHkPx,k/k-1,

(8)

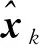
为了尽可能消除量测噪声时变的这部分影响，本文在利用Allan方差估计量测噪声的同时，加入了遗忘因子以及限定记忆长度的算法思想，实时估计量测白噪声方差参数，以期获得更为准确的姿态解算结果. 下面开始给出系统噪声方差和实时动态量测噪声的获取方法.

2.2　改进自适应Kalman滤波

2.2.1陀螺仪系统噪声估计

陀螺仪的系统噪声主要由陀螺仪系统内部机理决定，相对来说比较稳定. 滤波时，未知的噪声参数越多，滤波越容易发散，所以应尽可能减少未知噪声参数，并且相比于大数据量的静态测量，对系统噪声在线自适应估计的精度更低. 综合以上两点，本文对于系统噪声不采用实时估计的方法，主要利用Allan方差对MEMS传感器测得的静态数据事先进行建模分析，获得MEMS传感器误差的随机噪声种类，确定各项系数,从而求出系统噪声.

1) Allan方差原理

Allan方差是一种基于时域分析的分析方法，可以比较容易地对各种误差源以及整个噪声统计特性进行细致的辨识，获取随机噪声种类，确定噪声系数，因此被广泛地用来辨识惯性传感器的噪声误差源[9]. Allan可按式(9)来估算.

(9)

假设采样频率是fs，数据样本个数是M，则τL=L/fs，NL=M/L. 把数据样本分成L长度的串，计算每个数据串的平均值Ωk，然后按照式(9)计算.

对于陀螺仪而言，系统噪声主要有量化噪声(quantization noise, QN)、角度随机游走(angular random walk, ARW )、角速率随机游走(rate random walk, RRW)、零偏不稳定噪声(bias instability, BI)以及速率斜坡(rate ramp, RR)[10]. 这五种噪声可以通过 Allan 方差分析方法来辨识，并且误差分离结果较好，对应关系如表 1 所示[11].

表 1　常见噪声系数与Allan方差的对应关系

2) Allan方差分析

实验采用的是目前市场上比较常见的MPU6050姿态传感器，以100 Hz的频率在实验室单轴转台采集陀螺仪输出的静态数据，得到随机漂移数据样本，如图 2 所示.

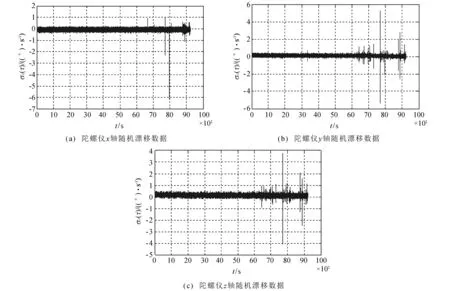
图 2　陀螺仪随机漂移数据Fig.2　Gyroscope random drift data

根据陀螺静态数据计算Allan方差，得到Allan方差的双对数图，如图 3 所示.

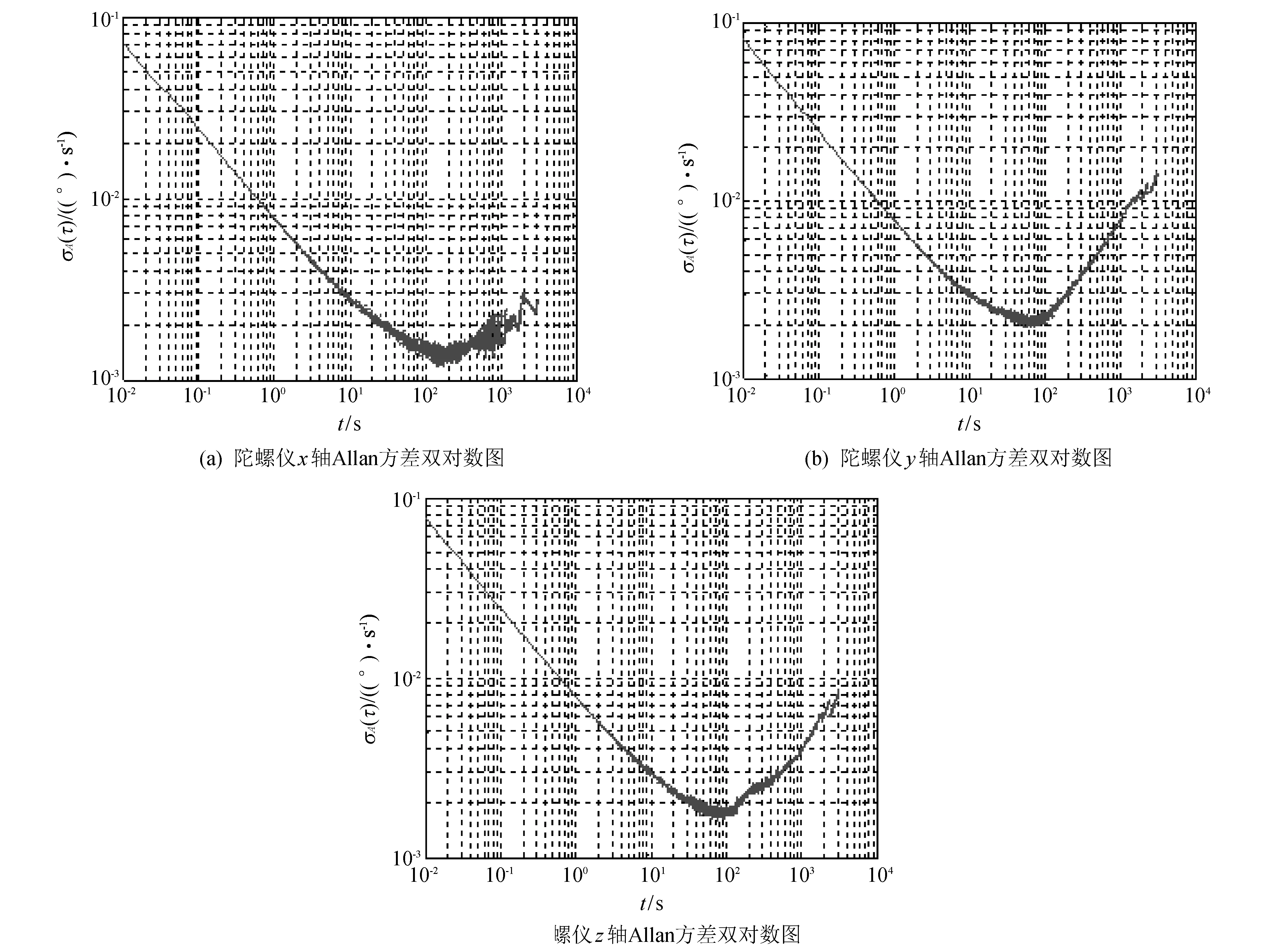
图 3　陀螺仪Allan方差双对数图Fig.3　Allan variance double logarithmic curve of gyroscope

根据Allan方差的双对数图确认该陀螺仪主要存在角速率随机游走、角度随机游走和零偏不稳定性3种噪声. 根据表1即可得到三轴陀螺仪的噪声系数，如表 2 所示.

表 2　各轴陀螺仪噪声系数

根据表 2 的数据分析可知，该陀螺仪的角度随机游走噪声系数较小，主要误差项为零偏不稳定性和角速率随机游走，以此两项求得白噪声方差作为系统噪声方差值.

2.2.2陀螺仪动态噪声估计

量测噪声主要由外部环境造成，容易发生变化，且存在一定的不可预知性. 因此，对量测噪声进行自适应处理，有利于保证系统滤波的稳定性.

本文在采用Allan方差来估计量测白噪声方差参数的同时，加入了遗传因子和限定于记忆的算法思想. 一方面对旧数据加入了遗传因子，降低了旧数据对误差辨识的影响，提高了新数据对误差辨识的作用； 另一方面，限定算法的记忆长度，即辨识数据达到一定个数的时候，每增加一个新数据，同时剔除一个旧数据，克服了仅带遗传因子的渐消记忆算法中老数据时刻影响辨识的缺点，更能有效地实时估计量测噪声.

式(10)是Allan方差估计公式的递推.

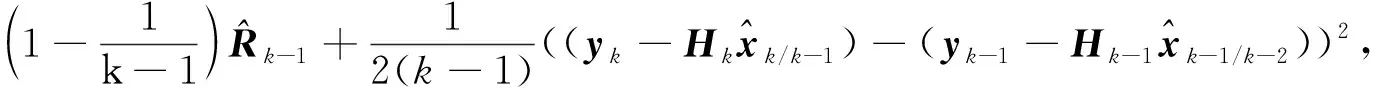
(10)

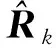
从式(10)可以看出，Allan方差递推公式最后得到的结果和带遗传因子的渐消记忆算法在形式上是一致的.

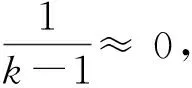
(11)

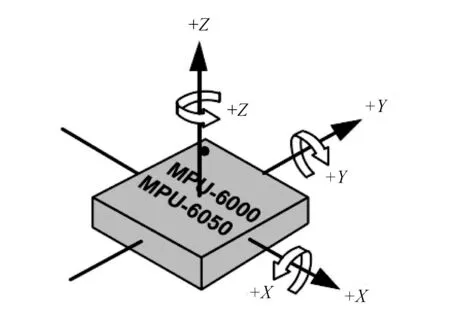
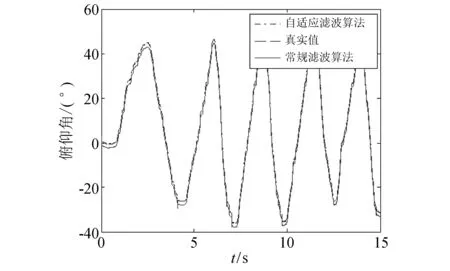
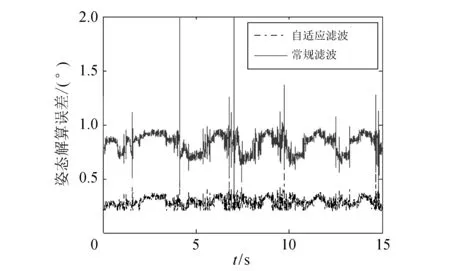
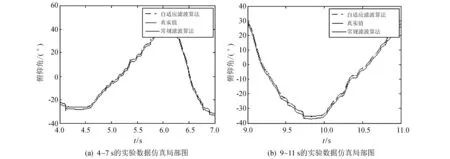
式中：b是一个常值，取值范围为0

通过调整常值b的大小，可适当调整过往数据在Allan方差计算中所占比重，相比较于式(10)可进行一定的比重调整，有利于提高辨识精度. 并且本文只利用最新固定长度的N个数据来递推方差值，这个固定长度可以利用Allan方差仿真已知数学模型方差变化的数据来估计得到. 通过多次实验仿真验证，本文中N取600时，既能保证数据方差的及时更新，也能使计算结果的波动尽量小.

当获取的数据长度大于固定长度N时，可以将式(10)转化为式(12)，即

(12)

3　实验仿真验证

图 4　MPU-6050传感器检测轴及其方向Fig.4　The detection axis and its orientation of MPU-6050 sensor

3.1　实验条件

本文所使用的姿态传感器为较常见的MPU-6050，内部集成有三轴MEMS陀螺仪和三轴加速度计. 为了应对实际使用中物体运动快慢的不同，传感器的测量范围以及传感器输出频率等等都可通过设置相关寄存器进行设定. 本文所设定的陀螺仪量程为±1 000 (°)/s，加速度计量程为±8g，姿态传感器的数据输出频率为100 Hz.

试验是利用摇摆平台在俯仰方向摆动来测取数据的，将MPU-6050安装在摇摆平台上，将Y轴平行于旋转主轴方向，MPU-6050和摇摆平台的俯仰运动方向保持一致.

在具体的试验过程中使用遥控器控制摇摆平台在俯仰方向进行随机角度摆动，在来回的摆动过程中采集三轴陀螺仪和三轴加速度计数据以及8191线编码器数据，其中，编码器数据得到的旋转角度精度小于0.04°，可以作为旋转过程中的真实角度值，以方便比较.

3.2　实验结果

多次进行俯仰方向的摇摆实验，利用采集到的数据通过本文改进之后的自适应滤波算法进行解算，同时通过常规自适应滤波算法计算，计算结果与真实角度值比照，求取误差的绝对值来作为精度比较的依据. 本文选取了其中一组实验数据仿真图进行分析，数据仿真图如图 5～7 所示.

图 5　实验数据仿真的整体图Fig.5　The overall map of experimental data simulation

图 6　实验数据仿真的误差图Fig.6　Error graph of experimental data simulation

图 7　实验数据仿真局部图Fig.7　The partial map of experimental data simulation

图 5～7 为本文摆动实验中采集得到的数据仿真图. 从仿真图 5 与图 6 可以发现，使用本文基于MEMS陀螺仪和加速度计的自适应算法解算出来的角度曲线和实际的角度曲线基本吻合； 通过图 7 可以发现，相对于常规的滤波算法，该算法解算出来的角度曲线更为接近编码器解算的实际角度曲线. 说明本文中提出的基于MEMS陀螺仪和加速度计的自适应算法有良好的抑制动态噪声能力, 能提高系统对环境变化的适应性，得到更好的滤波效果.

4　结　论

本文对姿态求解算法进行了一定的研究，提出了一种基于MEMS陀螺仪和加速度计的自适应姿态测量算法. 首先，通过对MEMS陀螺静态数据进行Allan方差分析，得到MEMS陀螺仪系统噪声估计； 然后，采用扩展卡尔曼滤波算法进行数据融合，同时，在对动态噪声估计的过程中加入了遗传因子、限定记忆长度的算法思想； 最后，通过实验和仿真，验证了本文提出的算法可有效地跟踪噪声参数的变化,提高了姿态角度测量精度.