基于波形特性自动识别的输电线路精确测距技术

张焕青，王 汇，裴知明，张 菁，李录照

（1.国网湖北省电力公司检修公司，湖北 武汉 430050；2.山东科汇电力自动化股份有限公司，山东 淄博 255087）

0 概述

输电线路故障行波测距技术［1-2］作为一种故障精确定位技术，在国内外电力系统得到了广泛应用。目前应用较多的是基于故障电流行波［3］的测距原理。从现场配置来看，如果在同一输电线路两端都配置有行波测距装置，在线路故障后，线路双端的行波测距装置通过通信网络交换故障数据，故障数据由基于全球定位系统的时间同步系统提供精度优于1 μs的时标，后台分析处理系统根据线路长度、波速度及带有精准时标的故障数据自动计算故障点距离线路两端的长度，这种配置是双端测距；如果线路只有一端配置行波测距装置，或者两端都配置行波测距装置，但两端行波测距装置之间不存在通信（往往由于两端变电站由不同电力公司管理），或者在输电线路故障时，一端装置故障或没有正常启动，此时只能依据线路一端行波测距装置的数据来判断故障距离，这种计算方式即为单端测距。

由于技术的限制，目前国内外除了双端配置能够由后台系统自动计算故障距离外，单端故障波形只能靠运维人员通过计算机辅助判定故障距离，处理时间往往过长且不确定 ，并且准确性差，有时不能够得出结果，判断失败。为解决此问题，有研究对单端波形进行自动识别，但从现场使用来看，目前尚无单端波形自动测距技术能够满足实际应用要求。因此，需要研发一种新的算法和后台软件，来解决输电线路故障后的单端自动故障计算。本文分析了输电线路故障行波特征，应用小波变换算法，提出了一种单端行波自动定位算法，并在实际线路上应用测试。

1 输电线路故障时暂态电流行波特性

单端测距原理利用故障时输电线路一端的暂态电流行波［3］波形，利用输电线路故障时在测量端采集到的初始暂态电流行波与该行波在测量端母线处的反射行波再次在故障处反射后到达测量端的行波之间的时间差，计算测量端到故障点之间的距离。

在一单相系统中，如图1（a）所示，在M侧对线路故障时暂态电流行波进行监测采集，当线路中F点发生接地或短路故障时，F点电压会发生突然的变化，因而会产生暂态电流行波，此行波以接近光速（一般为 291～294 m／μs）的速度向线路两侧传播。

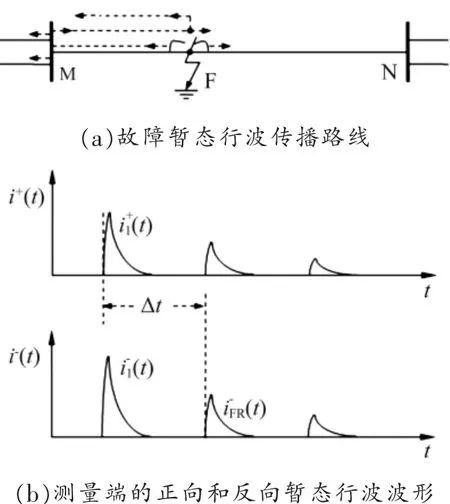
图1 单端行波故障测距原理示意图

为了更好分析，给向两侧传播的行波设定正反方向，远离测量端的行波定义为正向行波，反之则为反向行波。当故障初始暂态行波［3-4］到达测量端时，采集并记录其波到达时间为该暂态行波在测量端母线处产生反射，该反射波为正向行波，沿线 路向故障点传播，采集并记录此行波起始时间为该正向行波在故障点时产生反射，形成一个反向行波，采集并记录此反向行波到达测量端的时间为为了简化起见，不考虑其他的反射、折射行波，则输电线路故障时测量端采集的正向和反向暂态电流行波波形如图1（b）所示。

式中：v为暂态电流行波在输电线路中的传播速度。

在工程应用中，为了可靠地完成单端测距功能，要求在测量端必须能够准确、可靠地检测到初始故障波、反向反射行波的起始时间此时间精度要达到微秒。

根据输电线路故障时行波测距装置采集到的实际波形来看，根据故障点在输电线路位置的差异，暂态电流波形还具有以下特点：

1）当故障位置距离测量侧长度小于线路全长的1／2时，称之为故障在线路中点以内，如图2所示。在这种情况下，采集到的第二个行波波形是故障点反射波。

图2 故障点近测量侧（到测量端距离小于线路长度一半）

2）当故障位置距离测量侧的长度大于线路全长的1／2时，称之为故障在线路中点以外，如图3所示。在这种情况下，第二个行波波形是线路对端母线处反射波经故障点的透射波形，其波形初始极性和初始故障波形相反。

图3 故障点远离测量侧（到测量端距离大于线路长度一半）

如上文所述，在根据输电线路一侧采集到的线路故障波形进行人工单端测距时，首先需要识别出故障点反射波，以计算故障距离（这种计算一般计算机辅助），然后识别出对端母线反射波经故障点后的透射波，计算故障点到对端母线距离，最后将两个距离相加，得到的和是线路全长，据此验算测距结果是否正确，图4为实测波形。

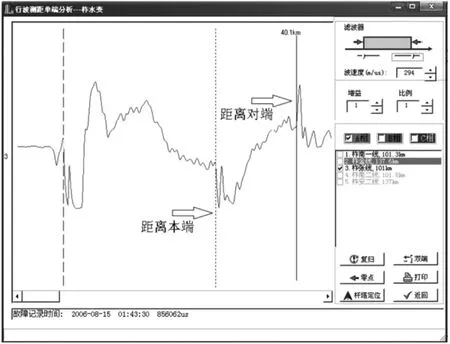
图4 单端测距实测波形

由上文分析可知，输电线路故障时所采集的行波波形具有以下几个特点：

1）故障初始行波幅值（能量）最大，然后故障的反射波、二次反射波、对端反射波等能量依次减少。

2）故障初始行波和故障点反射波、二次反射波的极性（波形向上还是向下）一致，但线路对端反射波经故障点透射后，其极性和初始行波、故障点反射波极性相反。

3）由图2、图3观察可知，故障初始行波和故障点反射波之间距离、故障点反射波和二次反射波之间距离相等，即具有周期性。

因此，为了准确进行输电线路故障时的单端测距，除了需要准确识别故障反射波外，最重要的是能够提取波头的准确起始时刻。

2 故障点反射波及二次反射波的判定及测距

2.1 故障反射波的识别及初始时间判断

当输电线路发生故障时，故障产生的电流暂态行波会沿线路传播，并在故障点及两侧母线处发生复杂的反射、透射。测量端的行波测距装置采集故障时的暂态电流信号，此电流信号一般来源于电流互感器二次侧，然后通过模拟或者数字滤波器获得行波波头脉冲。行波的折反射发生于线路的阻抗突变点，在母线处和故障点，电流行波产生正反射，故障点反射波与故障初始行波同极性，二者起始时间差值正好对应于行波信号在母线处和故障点之间往返一次的时间，被用来计算故障距离。

2.2 通过行波能量和法测距

为了实现故障时自动单端测距，首先需要辨别故障初始行波及故障点反射波，而这种辨别可以通过搜寻故障时线路上行波能量和最大点来实现。根据这个最大点来得到故障时间差，利用这个时间差计算故障距离。在获得故障数据后，行波测距软件对其进行保存，然后对数据进行分析处理，最后根据单端测距公式算出故障距离。假设有n个点，判断公式如式（2）、（3）：

通过对数据进行不同尺度下的分析，来自故障点的电流行波脉冲是在一个有效尺度范围内的极大值点，如果是一个小范围内的极大值点，则认为是干扰信号。对数据进行极性以及幅值的分析，可得到第一次波峰的最大值T1、第二次波峰的最大值T2。

设故障初始行波与由故障点反射波到达母线的时间分别为T1、T2，则故障距离可根据式（1）算出。

在输电线路故障时，无论是相间故障或者单接地故障，故障点一般存在过渡电阻。同时，对侧的反射波会在故障点通过过渡电阻或者健全相导引透射到测量端来。据节1所述，分别对故障点位于线路中点以内和线路中点以外进行分析判定，并根据本端反射波和对端反射波之间的关系进行校验，以计算故障距离。

故障暂态电流行波在沿线路传播时，会透射到同一母线上连接的非故障线路上，这些透射波在非故障线路上传播，并在线路对端形成反射，此反射波经过一定时间会再次传播到母线处并透射到故障线路上，造成采集到的故障暂态电流行波数量过多且波形复杂，这给故障点反射波或对侧母线反射波的识别带来了困难。但在实际工程应用中，当母线上连接的线路较多时，故障暂态电流在其他非故障线路上的透射电流幅值较小，可以忽略其影响，因此有用行波波形的识别就相对简单。考虑到此种情况，可以在算法中加入线路拓扑关系，以对此种波形进行判别并滤除。

2.3 利用小波变换技术判定波形起始时间

在实际工程应用时，上节所描述的初始行波和反射波之间时间差判定方法略显粗糙，达不到测距高分辨率的要求，一般只作为辅助判据。而为了更精准的进行行波起始时间判定，本文中采用小波变换［5-7］来进行波形极性和起始时间的精准判定。

小波变换是工程上被广泛采用的一种信号的时间－尺度（时间－频率）分析方法，不但具有多分辨率分析的特点，而且在时域和频域都具有表征信号局部特征的能力，被誉为信号分析的显微镜。小波变换在各种文献中多有介绍，本文不在赘述。

输电线路发生故障时，其暂态行波不是平稳变化的信号，具有突变性。相关分析表明，对于一个单独的模暂态行波［8］，它所包含的各种不同频率分量，其传播速度具有随频率降低而连续滞后的特性，因而使得其行波波头在沿线路传播过程中陡度越来越小（频散现象），给起始时间的判定带来困难。但对整体波形进行分析，暂态行波只在波头起始时刻表现出奇异性［9］，其他部分均不存在奇异性，因而不会出现行波频散现象，也就不会产生新的奇异点，仍可将突变点标定为行波波头起始时间。

本文采用二进小波变换［10］进行奇异点的检测，因为二进小波变换是完备的、稳定的，而且具有平移不变性，可以很好地应用到故障初始行波信号的奇异性检测中。

进行奇异性检测时，要先对混杂有噪声的信号进行平滑去噪，以减小噪声影响，然后对去噪后的信号求取一阶导数，根据导数极大值检测奇异点。也可采用平滑函数对被检测信号在不同尺度下进行平滑，然后求导检测其奇异点。多尺度边缘检测［11］和小波变换检测从算法上是等效的。

若实函数θ（x）满足以下条件：

则称该函数 θ（x）为平滑函数（SF），工程中一般采用高斯函数作为平滑函数。

假定平滑函数 θ（x）可微，并定义 Ψa（x）是 θ（x）的一阶导数，即：

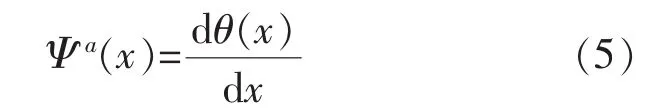
由式（3）可知，Ψa（x）可以被看作为小波，因为它们的积分为零，即：

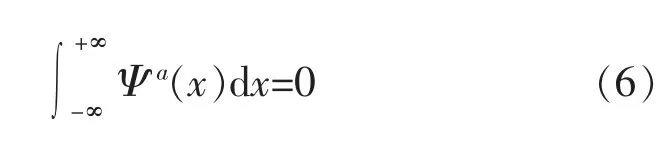
则函数 f（x）在尺度 s、变量 x 处关于小波 Ψa（x）的小波变换为：

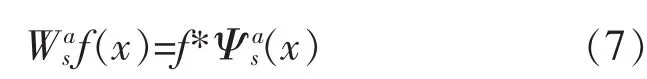
据此可以导出：

因为小波分量的模极大值［12］与信号突变点相对应，故可以确定行波起始时间，同时根据极值极性可判定波形极性。

由于小波模极大值检测方法不受信号幅度、信号上升速度以及信号检测灵敏度（门槛值）等因素的影响，因而所获得的故障初始行波浪涌到达时刻是稳定的。另外，由于小波模极大值检测方法本身具有较强的抗干扰能力，因而所获得的故障初始行波浪涌到达时刻也是比较可靠的。

3 单端行波波形分析算法

由第一节的分析可知，在基于单端波形的输电线路故障距离自动判定时，需要对波形的几个方面进行先期判定，然后才能计算出故障距离。其算法流程如图5所示，在此算法中数据采集后即对故障信号作相关预处理，以便以后的波形分析计算所需。每次故障反射波起始时间判定综合利用了上节中方法并进行了优化处理。

图5 行波测距单端自动测距流程图

根据以上算法流程，编写计算机软件程序模块，将此程序模块集成到行波测距装置的后台分析功能中，这样在线路发生故障后，行波测距装置除了和对端行波测距装置交换数据（存在对端并有通信的情况下）或将数据上传行波后台主站外（存在行波系统主站的情况下），还上报单端自动测距结果。此模块也可集成在行波系统主站侧，这样对于行波测距数据的处理除了基于双端及广域测距外，也可根据单端测距结果对故障距离进行综合分析，以进一步提高测距精度和可靠性。

4 实际分析结果

为了对以上算法进行验证，采用现场的实测数据输入后台分析软件由计算机自动计算故障距离并跟双端结果和现场实测结果进行对比，以确定该算法的可靠性和准确性，验证其为一个可行的方法。

将编写好的软件和原有行波后台分析软件进行了集成后，从现场调取实际输电线路故障后的故障行波数据，并将此数据输入后台系统进行分析计算，最后将结果进行了比对。

4.1 山孝线故障

山孝线从仙女山变至500 kV孝感变，线路全长54.9 km，500 kV仙女山变配置有行波测距装置，孝感变未接入此线路。山孝线实现了单端行波故障测距配置。

2016年7月20日输电线路发生故障，单端行波测试结果表明，仙女山变行波测距装置显示故障记录时间为2016年07月20日22∶46∶28，单端测距结果为故障点距离仙女山45.7 km，波形如图6所示，实际现场巡线结果为45.1 km，误差为600 m。

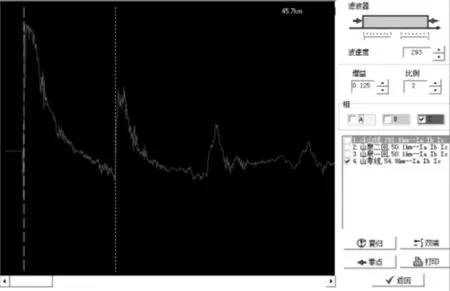
图6 山孝线故障单端测距结果

4.2 木泉线故障

木泉线从木兰变至500 kV柏泉变，线路全长67.3 km，500 kV木兰变和柏泉变配置有行波测距装置，木泉线实现了双端行波故障测距配置。

2016年7月14日，木泉线发生故障，两端行波测距装置都记录下了故障波形，柏泉变的记录表明故障发生时间为2016年7月14日03∶28∶12，双端测距结果为故障点距离柏泉变32.3 km，距离木兰变34.9 km，如图7所示。

图7 木泉线故障双端测距结果

为了验证算法，柏泉侧行波测距装置提供了自动单端测距结果，如图8所示，显示为32.6 km，和双端测距结果相差300 m；实际巡线距离为32.4 km，单端误差为200 m。

两次测距结果表明，单端自动测距误差满足现场巡线要求。

图8 木泉线故障柏泉侧单端测距结果

5 结论

本文通过对输电线路故障后故障暂态波形信号特性的分析，提出了利用能量最大法来区分疑似故障反射波，利用小波变换来确定故障波形极性以确定是否故障反射波，并判定故障波头起始时间，进而计算故障距离，最后通过故障初始行波和故障反射波、故障反射波和故障二次反射波之间的相似性来进行验证。利用现场实测的故障行波波形数据进行了算法测试，测试结果表明了算法的可行性，定位精度可以满足现场巡线要求。下一步，需要在现场运行中观察该算法对各种线路故障特别是复杂故障是否具备普适性，并对该方法进一步完善，以提高其可靠性和准确性。