基于灰色模型的全国棉花产量预测方法研究

2018-07-10梁后军谢睿冯宜强周万怀常郝李浩刘从九徐守东

中国纤检 2018年7期

文/梁后军谢睿冯宜强周万怀常郝李浩刘从九徐守东

1 引言

灰色系统理论是由华中理工大学邓聚龙教授于1982年提出并加以发展的。二十几年来，引起了不少国内外学者的关注，得到了长足的发展。目前，在我国已经成为社会、经济、科学技术等诸多领域进行预测、决策、评估、规划控制、系统分析与建模的重要方法之一。特别是它对时间序列短、统计数据少、信息不完全系统的分析与建模，具有独特的功效，因此得到了广泛应用。

在棉花产量预测方面，李鹏程、董合林[1]根据联合国模拟世界纤维市场的预测，认为2020年世界棉花产量预计将增加到3200万吨，其中发展中国家（地区）将继续占世界棉花产量的大部分份额。张闻、韩金等[2]通过多项式拟合的方法，针对2016年新疆棉花产量进行了预测，并基于预测对棉花加工工作提出了建议。本研究以2007—2017年全国棉花产量为基础，基于灰色系统建模方法逐步建立GM(1,1)模型，并外推预测2018、2019年的全国棉花产量，以期为棉花产业的生产、加工提供依据。

2 基于灰色模型的我国棉花产量预测

研究基于2007—2017年我国棉花总产量数据（数据来源：国家统计局网站），运用灰色模型GM(1,1)预测2018、2019年全国棉花总产量。灰色预测模型（Gray Forecast Model）是通过少量、不完全的信息，建立数学模型并做出预测的一种预测方法。目前常用的一些预测方法（如回归分析等），需要较大的样本。若样本较小，常造成较大误差，使预测目标失效。灰色预测模型所需建模信息少、运算方便、建模精度高，在各种预测领域都有着广泛的应用，是处理小样本预测问题的有效工具。只要待分析变量随着时间发展呈现有一定变化趋势，就可以尝试使用该方法进行建模，而无需考虑该变量的其他相关影响因素及状态；只要建模过程中每个步骤都符合模型的约束、检验准则，则可以认为模型合理、预测结果基本有效。运用GM(1,1)模型的预测步骤为：首先，对2007—2017年我国棉花产量统计数据进行预处理，降低其波动性，若处理后的数据的一阶累加和大致符合指数分布，则可以考虑建模；其次，建立、检验相应GM（1,1）模型拟合2007—2017年我国棉花产量，判断模型拟合效果；最后，运用GM（1,1）模型预测分析2018、2019年全国棉花产量。

2.1 灰色模型GM（1,1）原理

灰色模型是利用离散随机数经过生成变为随机性被显著削弱而且较有规律的生成数，建立起微分方程形式的模型。设n个元素的数列X(0)={x(0)(1)， x(0)(2)， …，x(0)(n)}，其中x(0)(k)≥0，k=1，2，…，n；X(1)={x(1)(1)，x(1)(2)， …，x(1)(n)}称为X(0)的一阶累加序列(1-AGO)，其中、k=1，2，…，n；灰微分方程为：

式(1)中a称为发展系数，b称为灰作用量，参数向量可以运用最小二乘法估计

其中Y，B分别为：

称为GM（1,1）的白化型，对应的解为：

当k≥n时，所求得的x(1)(k+1)就是x(1) 序列的预测值。由于

因此求得k≥n时的序列的值就可以利用（5）式求出X(0)序列的预测值。

2.2 数据预处理

由于灰色预测模型可以通过少量的、不完全的信息建模并预测。我们选择最近10年的全国棉花产量数据做建模基础。考虑到原始数据（为方便起见称其为X）存在较大波动，如图1所示，先对其进行最紧邻两两求均值处理，所得结果称为序列X(0)，即：

由图1可见X(0)比原始数据序列X波动稍小一些，以下以X(0)作为基础数据建立GM(1,1)模型。结合表1可以看出，从2008年开始，全国棉花产量总体呈下降趋势，特别是2016年棉花产量创下了近12年以来新低，宏观层面可能是受到了2008年开始的经济危机的影响，微观层面生产成本提高、种棉花不赚钱，棉农种棉积极性降低。

表1 数据预处理

2.3 数据检验

计算数列的级比若所有级比都在可容覆盖内，则数列可以作为模型GM(1,1)的数据进行灰色预测。否则，对数列进行变换处理，使其落入可容覆盖内。

本文中X(0)共10个数，即n=10，从而级比区间为（0.834, 1.199）。由于所有λ（k）ε（0.834，1.199），故X(0)可以用作为GM（1,1）的数据。

表2 级比检验

2.4 建模

由于GM（1,1）模型本质是建立指数模型，在建模前先要对X(0)序列求一阶累加和，得到X(1)序列，即对X(1)中每个元素，有 x(1)(k)=∑ki=1x(0)(i)，k=1，2，…，n；k=1，2，…，n；结果列于表3中。

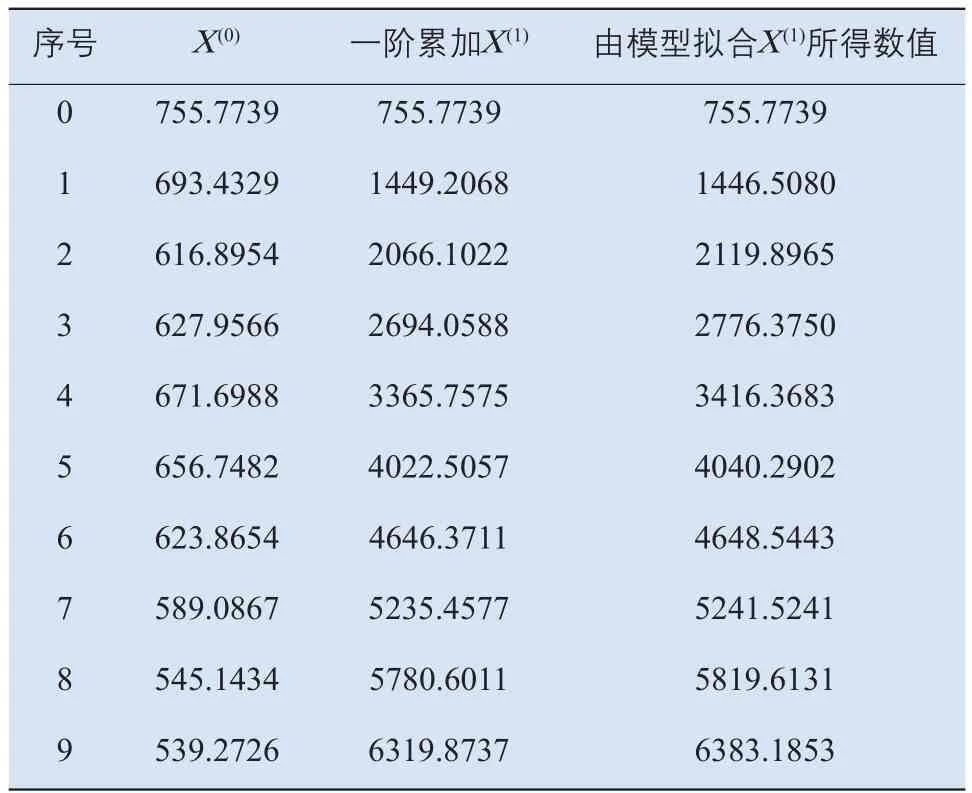
表3 X(0)的一阶累加X(1)及X(1)的模型拟合值

根据X(0)，X(1)构造矩阵Y、B，根据最小二乘法解得参数向量â=[a,b]T=[0.0254,718.7760]T，从而可得模型

解得

由公式（8）可以得到X(1)的模型拟合值，如表3所示。图1直观展示了X(1)及其模型拟合值的差异，由图中可见两条线高度重合，拟合效果较好。

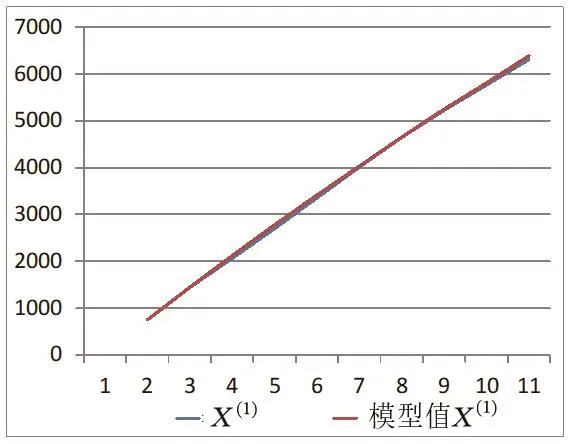
图1 一阶累加序列X(1)及其模型拟合值

根据公式（9）可以求得X(0)序列的模型拟合值，结果列于表4中。

图2直观展示了X(0)序列及其模型拟合值，除第三个数外总体而言拟合较好。

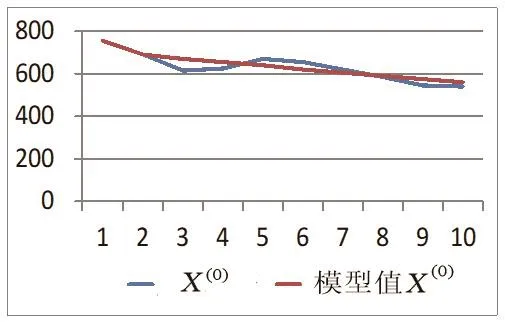
图2 序列X(0)及其模型拟合值

2.5 模型检验

一个模型能否用于预测，由有效性检验决定，只有符合检验标准的模型才能被用于进行预测。灰色模型检验主要包括平均相对误差检验、级比偏差值检验、绝对关联度检验及均方差比值检验。

1）相对误差检验：首先计算残差

相对误差序列为

对于k≤n，称为k点模拟相对误差，称为平均相对误差。本文中模型的平均相对误差为0.0375，对照表5可知模型精度为二级。

2）级比偏差值检验：首先计算级比，再利用发展系数a求出相应的级比偏差

若ρ(k)＜0.2，则认为达到一般要求；若ρ(k)＜0.1，则认为达到较高要求。本文中绝对值最大的级比是0.0958，小于0.1，说明模型达到了较高要求。

3）均方差比值检验：均方差比值为C=S2/S1，其中S2是由公式（10）计算得到的残差序列的标准差，S1是X(0)序列的标准差。由表4可知本文均方差比值C= 0.439，参照表5可知模型精度为二级。

综合以上3个指标可得本文的模型精度是二级。

2.6 预测

根据上面的检验可知，模型精度为二级，说明模型拟合精度较好。为预测未来两年的棉花产量，需要根据公式（8）计算X(1)序列的未来两点的值，如表6所示，X(1)序列的未来两点的值分别是6932.6053及7468.2283。再根据公式（9）可求得X(0)序列的未来两点值分别是549.4199及535.6230。

X(0)序列尚不是真实棉花产量，还需要根据公式(6)求多领域进行预测、决策、评估、规划控制、系统分析与建模的重要方法之一，对时间序列短、统计数据少、信息不完全系统的分析与建模，具有独特的功效，得到了广泛的出X序列未来两点的值，结果见表7，2018、2019年的预测产量分别为550.2398万吨及521.0062万吨。

可见未来两年，我国棉花总产量总体保持稳定，与2017年全国棉花总产量548.6万吨相比，2018年比2017年增长1.6万吨，2019年比2018年减少约29万吨。

表4 模型检验

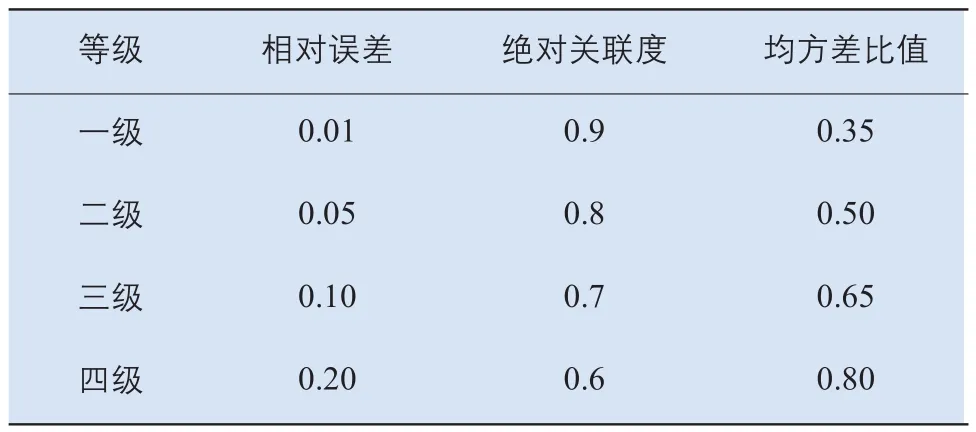
表5 灰色模型精度检验等级

表6 X(0)与X(1)序列数据预测

3 总结与讨论

灰色系统理论已经成为社会、经济、科学技术等诸应用。该法无需考虑客观事物之间的关系及影响预测对象因素的多少，仅依据连续收集预测对象过去的统计数据，即可找到其随时间变化的规律，建立时序模型，对未来进行预测。整个建模过程步骤清晰，操作简便，短期预测结果可靠。本文利用2007年至2017年全国棉花总产量资料进行分析，通过中值化运算、模型拟合与检验等过程建立GM(1, 1)模型，探讨未来两年棉花产量的预测值。模型精度达二级标准，准确度较高。诚然，灰色模型仅作为一种数学预测工具，所依据资料的样本含量有限，得到的也仅是理论值，难免会带有局限性，为达到有效预测的目的，在使用时应结合动态监测，不断更新数据对模型动态拟合，从而保持较高的预测精度，更加有效指导我国棉花种植与交易工作。