“反比例函数”教学浅析
2018-07-09黄春秋
黄春秋

【摘要】本文从突出反比例函数与生活的联系、在教学过程中注意渗透思想、关注函数学习方法的科学指导三个方面对“反比例函数”教学展开探讨。
【关键词】反比例函数 联系实际 思想 方法学法指导
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2018)04A-0127-02
函数是描述现实世界自然变化规律的一种数学模型,反比例函数是基础函数之一。反比例函数的教学是在学生已经掌握了平面直角坐标系和一次函数的基础上开展的,函数概念、图象与性质是核心知识,教师在教学时要采用合理教法,突出重点。
一、突出函数与生活的联系
反比例函数是反映现实世界特定数量关系的一种重要的数学模型,其相关知识在日常生活、生产实践和科学研究等方面有着广泛的应用。因此,教师在教学反比例函数时要紧密联系生活实际,重点突出反比例函数与现实生活的联系。
教师在刚开始教学反比例函数的相关知识时,有必要引入大量的实际问题,在激发学生学习兴趣的同时让学生深刻体会反比例函数在现实世界的广泛应用。教师可以创设如下情境:①小明和爸爸准备用旧的围栏围成一个面积为10m2的花圃,假设它的一边长为x(m),请写出另一边长y(m)与x的函数关系,10=xy;②小红的爸爸驾车从美丽的青岛去到济南,汽车里程表显示为350km,请大家说出行驶时间t与行驶速度v的函数关系,350=vt。教师从学生的生活圈中选取的问题,符合学生的认知发展规律,可让学生更自在、放松地参与问题讨论,同时也使学生真切体会到生活中处处充满函数,意识到研究函数的必要性。
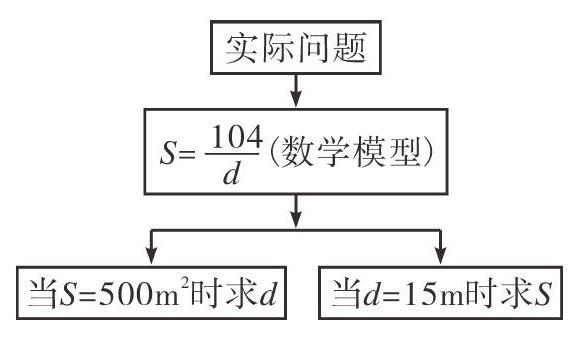
其次,在运用知识阶段,教师也需要充分结合实际,引导学生运用反比例函数的相关知识分析、解决问题,在巩固学生知识的同时,提升学生解决问题的灵活性。教师可以设置如下问题:某煤气公司需要在地下扩建一个容积为104m3的圆柱形储藏室,①储藏室的底面积S(单位:m2)与深度d(单位:m)有着怎样的函数关系?②如果将储藏室的底面积S定为500m2,施工时应该向下挖多深?③如若临时将储藏室深度定为15m,相应的底面积应改为多少?教师结合上述问题对学生进行合理引导,让学生体会反比例函数是描述现实世界的有效工具,初步培养学生设计方案、解决问题的能力。
反比例函数教学与生活实际的有效结合对于学生深刻体会函数在生活中的广泛应用有着极大的帮助,而利用反比例函数解决实际问题,可让学生体会到“理论来源于生活,又反过来指导生活实践”的哲学思想。
二、注重数学思想方法的渗透
虽然反比例函数是一种较为基础、初等的函数,但是其中蕴含了丰富的数学思想方法,对提升学生的观察、分析、解决问题的能力有极大帮助。
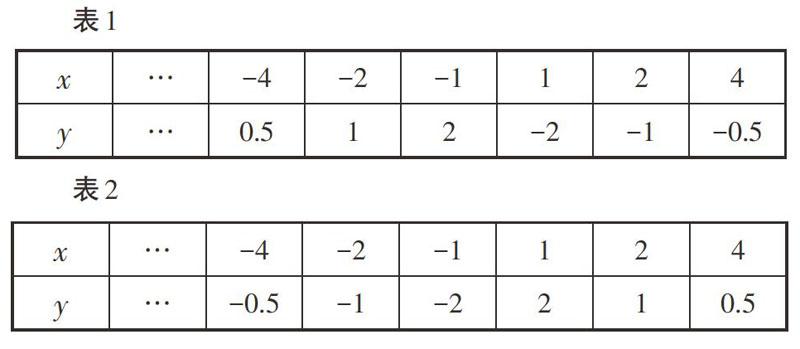
反比例函数的教学是在概念教学的基础上开展的,教师在教学中可有效渗透归纳和对应的思想。例如在抽象概念阶段,教师引导学生分析几个具体的问题,如分析表1和表2中的因变量与自变量的变化规律,分析函数变量x与y之间的对应关系,并渗透对应的数学思想方法,然后进一步归纳反比例函数的共同特征,抽象出反比例函数的概念,渗透由特殊到一般的数学思想方法。
反比例函数的图象与性质的教学应该围绕数形结合思想来开展,反比例函数的图象与性质本身就是“数”与“形”的统一体,对图象的分析充分体现了数形结合思想。学生在学习数轴和平面直角坐标系时已初步了解了数形结合思想,教师在教学反比例函数阶段需要利用函数的图象优势引导学生深入理解数形结合思想,如设定由“函数解析式”到“作图表”的环节,然后利用“图表”探究“图象的性质”,让学生充分体会由“数”到“形”,再由“形”到“数”的转化过程,体会其中的数形结合思想,并利用函数解析式及性质与图象的联系,让学生深刻体会转化思想对于分析问题的重要作用。
此外,教师要适时渗透数学模型思想,通过对知识的回顾,引导学生将问题转化为函数模型,然后利用函数模型的直观便利性有效分析问题。例如,教师可以以这样的思路讲解上述煤气公司挖储藏室的问题(如下图):首先根据圆柱体的体积公式,建立底面积S与深度d的关系,即数学模型S=[104d],然后根据模型分别求两种设计情形下的具体量,即已知S求d,已知d求S。教师通过建立数学模型,引导学生掌握解决实际问题的方法,渗透模型思想,提升学生思维品质。
反比例函数的教学应该以数学的思想方法作为主要线索,以突出变化与对应思想、归纳思想、数形结合思想和模型思想作为教学的首要任务,合理设置教学环节,充分渗透数学思想。知识对学生的影响是浅薄短暂的,而思想方法则会使学生一生受益。
三、关注函数学法的科学指导
对于反比例函数教学,教师可以采用一般函数的教学模式,即“函数概念—函数的图象和性质—应用函数解决问题”,参照一次函数的教学方式,采用“异课同构”的方式开展教学。教师首先需要明确教学任务,准确定位知识地位,完善学生的认知结构,然后通过联系旧知、结合实际,帮助学生理解函数概念,再依照上述结构深入开展教学。对于反比例函数图象的学习,教师可采用作函数图象的一般方法,即描点法,首先分析函数解析式的自变量的取值范围,建立x与y取值的对应变化表格,然后建立直角坐标系,构思函数图象的位置、轮廓以及变化趋势,通过描点、连线的方式来作图。
教师在教学反比例函数时也可以对比正比例函数相关知识来加强学生对反比例函数的学习,通过设问的方式让学生多方面对比反比例函数y=[kx](k为常数,k≠0)与正比例函数y=kx(k为常数,k≠0):
①两种函数的解析式存在哪些異同?其图象有何差异?
②在常数相同的情况下,自变量x与因变量y有何变化趋势上的差异?
③两种函数在自变量x的取值范围上有何差异?常数的符号变化是否会影响函数图象所处的象限?
教师对比正比例函数设置相应的问题,通过设问、列表(如表3所示)回答的方式引导学生学习反比例函数的相关知识,整个过程让学生完成对知识的梳理,同时以探究的方式学习新知,学生的数学思维和学习兴趣也可以最大程度地被激发出来,对于牢固掌握知识有着极大帮助。
总之,对于反比例函数的教学,教师要准确把握函数的核心知识,从现实生活中抽象反比例函数概念,使学生对生活的感性认识上升到理性认识,结合生活中的实际问题开展应用教学,努力提升学生解决实际问题的能力;注意渗透数学的思想方法,让学生充分感受归纳、对应、数形结合和模型思想,为学生的终身发展提供助力;采用科学合理的教法,参照一次函数的学习方式,通过探究合作、对比归纳的方法来指导学生学习反比例函数的相关知识,努力提升学生的分析问题能力及数学表达能力。
(责编 刘小瑗)
