画图策略在解决数学问题中的实践探究
2018-07-09蒲健强
蒲健强


【摘要】画图策略的运用能把复杂难懂的问题具体化、形象化、直观化,帮助学生厘清解题思路,快速解题。本文提出了三种提高学生画图能力的方法,即指导学生会看图、识图,引领示范、耐心指导,加强作图训练、规范作图。
【关键词】小学数学 画图策略 实践探索
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2018)04A-0093-03
画图,能把复杂难懂的数学问题具体化、形象化、直观化,帮助学生厘清解题思路,快速顺利找到解决问题的途径,是学习数学的重要策略之一。画图,既是教学的重点,也是教学的难点。笔者发现,画图法是架起学生与问题之间的桥梁,让问题变得简明、清晰。因此,在课堂教学中,教师不但要教会学生找到问题的答案,还应教给学生解決问题的方法,体会画图的优越性,从而喜欢用画图的策略来解决数学问题。
一、初步感受画图策略的优越性
一年级学生的认字量少,对一些抽象的文字的理解有一定的困难,很难读懂题意,也有些学生不愿意读题,懒得读题。教学时,笔者抓住低年级学生的年龄特点,让他们在纸上涂一涂、画一画,进而在画图的过程中体会方法,发展思维,并在解决问题的过程中发现画图的优越性。
例如,在教学一年级上册“排队问题”时,教材呈现了如下情境图:
问:小丽和小宇之间有多少人?
学生读题后,还是说不清题意。对于一年级学生来说,他们的抽象思维能力有限,在理解“排队”这个问题上有较大的困难。“看看谁想到了好的办法?”时间一分一秒地过去了……这时,有一名男生举起了小手,站起来说:“老师,我有方法!”“好,说说你的方法!”“我画了一个图,用一个圈表示一个人……”“真是个好方法!画一画就行了!”笔者因势利导,引导学生动手画一画。
这样呈现出来的图形直观明了,学生一看就知道小丽和小宇之间有4人,初步感受画图策略的优越性。
又如,从前往后数,第4只是
笔者提示学生:“根据‘从前往后数,第4只是小猴,怎样画出小猴的位置?”学生有了上一次画图的经验,直接在纸上从左边起画了4个圈,并把第四个圈做了记号。然后笔者接着问:“从后往前数,第6只是小猴,那么小猴后面的小动物又怎样画出来呢?”这时教室热闹了起来,学生纷纷举手争抢着要把自己的答案告诉老师:“从后面画上来……”通过师生的共同努力,画出了如下的图形,学生很容易就解决了问题,再次感受到了画图策略的优越性。
二、认识到画图在解决数学问题中的重要性
画图可使题目内容直观化和数量关系明朗化。在分析问题后,教师要引导学生根据题意画出草图,使抽象的数学问题形象化、直观化,并且能化隐性为显性、化复杂为简单,便于学生理解和记忆,进一步厘清解题思路,找到解决问题的方法。
例如,“求一个数比另一个数多(少)几”的问题:有两只小猫在钓鱼,小黄猫钓到了7条,小花猫钓到了12条,小花猫比小黄猫多钓了多少条?
师:从问题中你知道是谁和谁比吗?
生:小黄猫和小花猫比。
师:谁多、谁少?
生:小花猫多,小黄猫少。
师:为了让我们能更清楚地知道小黄猫和小花猫之间有怎样的数量关系,我们可以用画图的方法来看一看,想一想。(如下图)
小黄猫:○○○○○○○
小花猫:□□□□□□□□□□□□
师:从图中你能看出小花猫比小黄猫多钓几条吗?
生:小花猫比小黄猫多钓5条。
师:你是怎么比较的?
生:将小黄猫和小花猫钓鱼的条数一一对应画出来,对完后,小花猫的条数还剩5条,也就是图中画多的那5个正方形,所以小花猫比小黄猫多钓了5条。
师:其实在我们比较的时候,把小花猫钓的条数看成了几个部分?
生:两个部分。
师:哪两个部分?
生:一部分是和小黄猫的同样多,另一部分是比小黄猫多钓的那部分。
师:谁能上来把这两部份用竖线分一分呢?
(让学生先在自己的纸上分一分,再指名一名学生上台来分一分,并说出各部分表示的含义)
小黄猫:○○○○○○○
小花猫:□□□□□□□□□□□□
同样多的部分 多的部分
师:通过刚才的理解,小花猫比小黄猫多钓了多少条,你能用算式表示出来吗?
生:12-7=5(条)。
师:为什么要用减法来计算?
生:小花猫比小黄猫多钓了多少条,就是要从小花猫钓的条数中去掉和小黄猫同样多的7条,剩下的就是小花猫比小黄猫多钓的部分,所以要用减法。
理解题中的数量关系是这节课的教学重点,难点是理解为什么要用减法计算。为了能让学生更好地理解,笔者通过画图的方式把文字转化成图形,并用一一对应的方法感知谁多谁少、多了多少等问题,明确数量关系,问题也得到了有效解决。
三、画图意识在课堂教学中的培养
在实际教学中,笔者认为,要培养学生的画图意识,教师要做好引导,不能急于求成,做到慢慢渗透。教师可以从以下三方面培养学生的画图意识。
(一)让学生在厘不清题意时通过画图来理解、读懂题意
在日常教学中,笔者发现学生在解答含有图形的数学题时往往比纯文字的数学题正确率高,因为纯文字的问题在语言表述上显得比较死板、枯燥。另外,由于学生的抽象思维能力比较弱,在遇到纯文字的数学问题时往往从心理上就认定了类似这种题型的题很难理解,所以有些学生根本就不愿意读题。当学生出现这种情况时,教师要借助“图”引导学生观察、分析题意,明白问题的基本意思,从而让学生读懂题意,理解问题。
(二)鼓励学生在解决问题缺乏思路时画图分析
面对纯文字的数学问题,特别是行程、工程类题型,学生往往很难读懂题目的意思,不知道解决问题的思路,更不要说找数量关系了,导致大部分学生缺乏解题思路,无从下手。教学时,教师可以用图形表示题目中的条件和问题之间的关系,为学生顺利解题提供帮助。
(三)在数量关系不明的情况下,借助画图提高学生分析问题的能力
小学阶段常见的应用题中有些数量关系不太明显,仅凭文字的叙述學生很难理解。为了能正确审题并找准题中的数量关系或对应分率,教师可以借助画图的方法引导学生理解题意,掌握找准数学关系的方法,进而快速分析题意,快速解答。
四、指导画图方法
小学生的思维处于具体形象思维发展的初级阶段,笔者在教学中发现,不会画图或不懂如何画图的学生还有不少,他们在解题时缺乏通过画图来解决问题的意识。因此,教师要善于培养学生的画图意识,通过引领示范、细心指导学生画图,帮助学生掌握画图的方法和技能。
(一)指导学生学会看图、识图
画图,是在学生会看图、认识线段图的基础上才能进行的,如果线段图都看不懂,那就不可能画出正确的线段图。因此,教师要认真研读教材,相机引导,让学生认识图、读懂图、理解图,理解图画表征的特点,进而不断积累画图解决问题的经验。
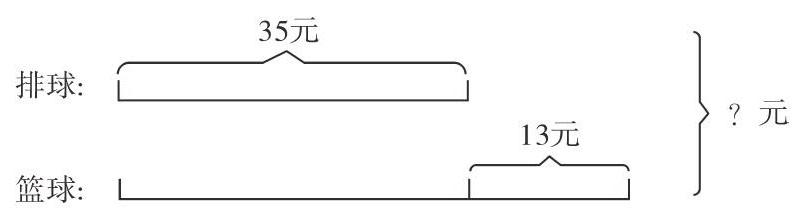
如:一只排球35元,一只篮球比一只排球贵13元,问一只排球和一只篮球一共多少元?学生独立完成后,笔者发现有部分学生只用了一步计算:35+13=48(元)。此时,教师可以指导学生画出如下所示的图形:
接着,引导学生看图,让学生说说已知什么条件,要求什么问题,该怎样思考。有些学生在观察之后,还是找不到错误的原因。紧接着,笔者再次引导启发:“算式中的‘35指的是哪一部分线段?‘13呢?这两个数分别表示什么?”这时,学生终于明白错在哪里了,原来他们求出的只是篮球的价格,最后还应加上排球的35元,这才是问题的答案。
(二)引领示范,耐心指导
小学生正处于模仿性很强的阶段,教师的一笔一画、一言一行直接影响着学生。教师在板书画图时应规范、准确,图形线段长短的比例要拿捏准确,还要让学生明白先画什么,再画什么;题中的已知条件和问题怎样在图中标出来,进一步明确所画的图形要与数量关系一致。
如在《倍的认识》一课中,由于学生第一次接触线段图,教师可以先让学生通过摆一摆、圈一圈的方法初步感知画图,继而把这些实物、符号演化成一条条线段。此时教师顺势启发学生思考:先画什么?如何恰当地确定“一倍量”?这“一倍量”就是一个单位长度,一般要先画,那么究竟要画多长呢?一倍量画得太长,几倍量不够画;画得太短,整体看起来也不协调。这时就需要教师做出示范,并告诉学生,通常画“一倍量”的长度要看看后面的另一个量是“一倍量”的几倍,倍数是3-4倍的,“一倍量”一般画1厘米左右,倍数多的就相应的画短一点,并且每条线段的左端要对齐,这样便于比较。这样,在教师的示范、指导下,师生共同完成线段图,让学生加深了对“倍”的认识。
(三)加强作图训练,规范作图
教师除了让学生学会识图,还要训练他们的作图技能。例如,画线段图时几个对比的量要用不同的线段表示;互相包含的量可以画在同一条线段图上。画图时,一般先画被比较的量(分数、百分数问题先画单位“1”的量),图中要完整表达题意,所有的条件和问题都要标清楚。
总之,运用画图策略解决问题,是一个重要的数学思想,又是一种常用的数学方法。教师应有意识地培养和加强学生的画图能力,让学生在学习中多角度、多方面感受图形的优越性,让题意的理解、解决问题突破口的搜寻,解题思路的形成都能从图中获得,并且通过积累画图经验,在以后的学习中逐步形成自觉运用的意识,让画图慢慢内化为学生的一种解决问题的策略。
