一元等熵恒定气流理论的追溯和解读

卜银坤

(北京航天动力研究所 北京航天石化技术装备工程公司, 北京 100076)

一元等熵恒定气流，是指一定质量的可压缩理想气体在单一方向上无摩擦损失的绝热流动。一元等熵恒定气流理论的特征方程，主要有连续方程、运动方程、状态方程、能量守恒方程和动量守恒方程，这些方程的特性参数之间存在固有的动力函数关系，按这种函数关系代入不同的数据，将结果列成表格，即构成气体动力函数表，可为工程设计提供重要参考。由于一些书本和资料中对这些方程的来历介绍得不够连续、透彻，逻辑关系交待不清，有的只给出了结论，连单位都没有给出，使学习和使用都极为不便，因此，本文追溯和解读了这些方程的来历、适用条件及有关参数的单位，以便大家能正确灵活地应用这些公式，创新性地解决航天、航空、节能环保等领域中的现实问题。

1 状态方程

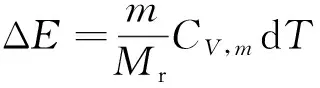
(1)

等熵恒定流动气体的各种状态，必须同时符合理想气体在任何情况下的门捷列夫·克拉珀龙方程，即必须遵守压力、体积、温度间的不变关系：

(2)

绝热是等熵流动的必要条件，气体在绝热流动过程中，式(2)中的p、V、T既是自变量又是因变量，即p=φ(T,V)，V=Ψ(T,p)，T=f(V,p)。式(2)两边对变量T进行一阶全偏导，写成微分方程为

(3)

(4)

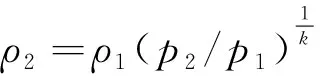
2 运动方程和能量守恒方程

一元等熵气流的能量守恒方程，实际上是可压缩气体在单一方向上无摩擦损失的绝热流动中公认的伯努利方程。

众所周知，一元恒定流动、无黏滞性理想流体的运动方程，即为基于牛顿第二定律的欧拉公式[2]，它既适合不可压缩流体，也适合可压缩流体，忽略重力后为

(5)

由式(4)得可压缩气体在等熵流动过程中，

(6)

应用微分、积分的概念，将式(6)作如下变换

(7)

将式(7)代入式(5)并积分得：

(8)

在式(5)和式(8)中，v为气体的流动速度，m·s-1；C2为恒量。因为式(4)的变换代入，所以，式(8)是所有可压缩流体的能量守恒方程。因为形式上类同常规不可压缩流体的伯努利方程，所以，式(8)也称一元等熵恒定气流的伯努利方程。

由热力学[3]可知， 1 mol气体在温度为T时的焓值H，实际上是热力学能U(U=CV,mT)和流动方向上所具有的推进功RT(pV=RT)的和，即

将该式代入式(8)，即得：

(9)

其中，C3为恒量。应当说，式(9)是一元等熵恒定气流能量守恒方程的热力学表达式，说明气体在绝热无外力做功的特定情况下，动能的增加量等于气体焓值的减少量。因为焓值的变化意味着温度在变化，所以式(9)揭示了可压缩气体流动速度会改变其温度的事实，也正是这个原因，虽然在数值上C3=C2，但是二者的物理意义却大不相同，C3具有深刻的物理内涵，而C2不过是一个简单的积分常数。因此，可压缩气体与不可压缩流体在流动过程中的显著区别在于，前者温度随着速度的增加而减小，或随着速度的减小而增加；而后者的温度，除了对外界进行热交换外则是恒定的。

3 一元等熵恒定气流能量转换的特点

为说明一元等熵恒定气流能量转换的特点，首先了解不可压缩的理想流体，在不计重力，且初始位置为滞止状态的伯努利方程[4]或能量守恒方程，即

(10)

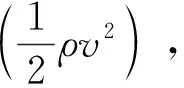
即

(11)

又因为

(12)

将式(11)两边分别除以式(12)可得：

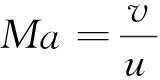
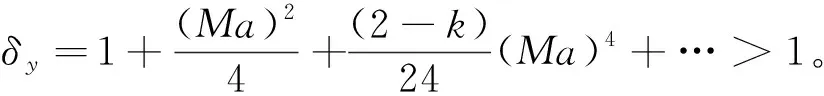
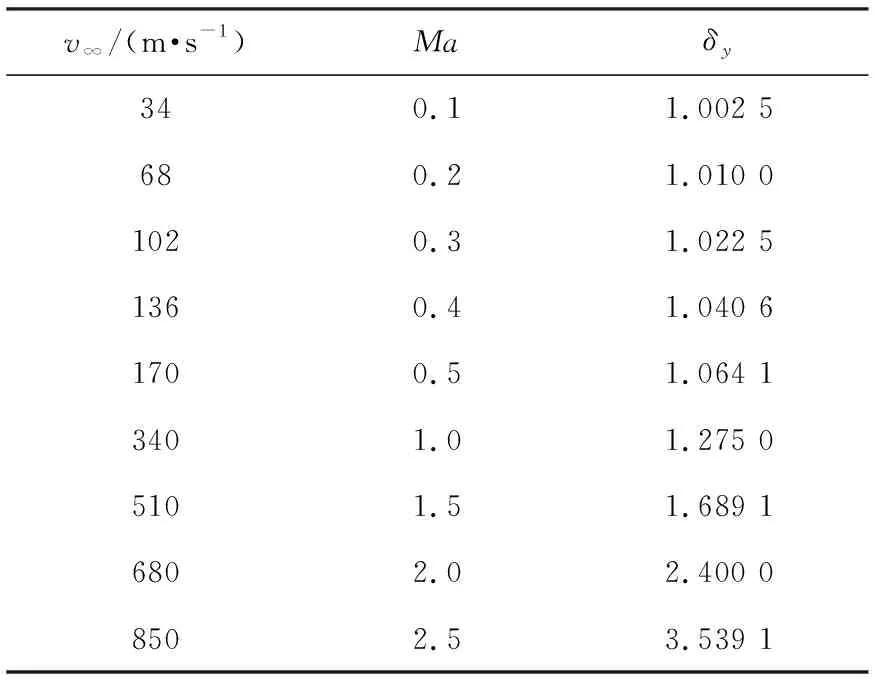
表1 一元等熵恒定空气流动时，不同马赫数 对应的能量转换系数Tab.1 Energy conversion coefficient δy at different Ma for the one-dimensional isentropic constant airflow

比较式(13)和式(10)，或分析表1的数据不难看出：与不可压缩流体不同的是，一元等熵恒定气流的压力转换为动能的本领随着马赫数的增加而减小，这是可压缩气体和不可压缩流体在流动过程中的另一显著区别。当Ma<0.3时，如果将可压缩气体视为不可压缩流体计算，则与Ma趋近于零时的流态比较，计算出压力转变为动能的值会增加1.022 5-1=2.25%，显然，Ma越大，能量转换的效率就越低。

4 连续方程及速度对流动参数的影响

气体在管内作恒定流动，是典型的一元恒定管流，根据物质不灭定律，最能被接受的流动连续方程为

qm=ρvS=ρΔV

(14)

其中，qm为气体流动的质量流量，恒定流动时，qm为恒量， kg·s-1；S为气体流通的截面积，即与流速v和密度ρ对应的流通截面积，m2；ΔV为单位时间内流过截面S的气体体积，m3。

对式(14)两边取对数得lnqm=lnρ+ln(ΔV)，两边全微分得：

(15)

(16)

将式(16)代入式(15)得到密度的相对变化为

(17)

则动能相对变化为

(18)

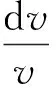
5 一元等熵恒定气流的动力函数关系

设一元等熵恒定气流初始位置的滞止压力、密度、温度、声速分别为p0、ρ0、T0、u0，流动到任何一个位置的动态压力、密度、温度、声速分别为p、ρ、T、u，临界位置对应的压力、密度、温度、声速分别为p⊗、ρ⊗、T⊗、u⊗。按有关理论方程推导出两个位置相应参数之间的比值与马赫数之间的函数关系，即气体动力函数关系如表2所列。表2中的函数关系是一元等熵恒定气流中，各动、静相应参数比值与马赫数之间固有的函数关系。按照表2的气体动力函数关系原则制作的气体动力函数表，可供产品或工程设计时查表使用。若要避免插入法查表带来的麻烦和精确性差的问题，可以直接采用表2中的动力函数关系式进行计算。

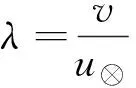
(19)

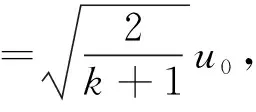
表2 一元等熵恒定气流不同位置的动态参数与滞止参数之比同Ma或λ的函数关系Tab.2 Functions between ratios of dynamic parameters at different positions to hysteresis parameters and Ma or λ in one-dimensional constant isentropic airflow

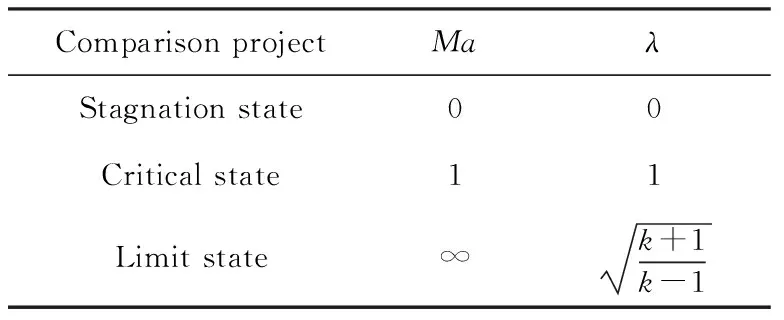
表3 几种特殊情况下Ma与λ之间的数值关系Tab.3 Numerical relationship between Ma and λ in several special cases

值得指出的是，因为气流的速度系数λ是相对临界声速的，所以按λ计算得到的数值均为临界值，对此，设计时应根据存在的摩擦、散热、泄漏等不可逆因素做适当修正，尤其在设计用常温空气引射1 000 ℃高温烟气的引射器时，应当格外谨慎，否则设计将是失败的。

6 动量守恒方程

一元等熵恒定气流的动量守恒方程，是指气流两个关键流通截面之间，气流质点系所受外力与其机械运动量在同一方向上的平衡关系，借此关系可求解维持气流设计的流动参数所必须提供的外力。值得提醒的是，用于产品或工程设计时，必须考虑一定程度的摩擦、扰动、散热、泄漏等不可逆因素对流速的影响。例如，在负压吸气式高温烟气引射器的动量守恒方程[6-7]中，对工作气体和引射高温烟气，必须计入小于1的速度系数φ；对混合气体，必须考虑速度的不均匀系数Ψ；对气流的高温段和次高温段，必须考虑一定的散热影响系数τ。

7 结束语

1) 一元等熵恒定气流的流动特性不同于不可压缩流体，除了前者密度是可变的而后者密度是恒定的以外，最大的区别有两点：

二是在流动过程中压力转变成的动能，前者小于后者，二者的偏差随着速度的增加而增大。

理论计算表明：将一元等熵恒定气流按不可压缩流体计算，得到的速度会偏大，偏差将随着Ma的增加而增加；当Ma<0.3时，按不可压缩流体计算，会造成动能偏高约2.25%，速度偏高约1.2%，体积偏大约0.15%，密度偏低约0.15%，各项偏差均在工程设计的允许范围内，因此，可以将可压缩气体当作不可压缩流体来计算，这样可以大大降低计算的复杂性。

2) 一元等熵恒定气流过程中，能量的转换效率随着Ma的增加而减少，而Ma又是气流设计中的重要参数，因此，需要慎重、有据、科学地确认Ma值。

3) 一元等熵恒定气流的状态有3种：滞止状态是速度v=0时的状态，对应参数称为滞止参数，是状态参数中数值最大的；动态是v≠0时的状态，对应参数称为动态参数，因为动态是常态，所以可以直接称为状态参数；临界状态是速度与当地声速相等时的状态，是动态中的特例，即v=u或v⊗=u⊗时的状态，相应参数即为临界参数。

4) 应用一元等熵恒定气流的相关理论进行产品设计时，必须首先满足或基本满足绝热良好、阻力较小的流动环境，确保流动可以近似为等熵过程，否则再精确的设计也是有问题的。

[1]王谟显. 物理学 [M]. 2版. 北京: 高等教育出版社, 1963: 144-184. (WANG Mo-xian. Adaptation Physics [M]. 2nd ed. Beijing: Higher Education Press, 1963: 144-184.)

[2]西安交通大学流体力学教研室. 流体力学 [M]. 西安: 西安交通大学出版社, 1964: 230-251.(Department of Fluid Mechanics, Xi’an Jiaotong University Press. Fluid Mechanics [M]. Xi’an: Xi’an Jiao Tong University, 1964: 230-251.)

[3]王补宣. 热工学 [M]. 3版. 北京: 人民教育出版社, 1964: 38-72.(WANG Bu-xuan. Thermo Engineering [M]. 3rd ed. Beijing: People’s Education Press, 1964: 38-72.)

[4]孔珑. 工程流体力学[M]. 3版. 北京: 中国电力出版社, 2006: 149-181.(KONG Long. Engineering Fluid Mechanics [M]. 3rd ed. Beijing: China Electric Power Publishing House, 2006: 149-181.)

[5]中国矿业学院数学教研室编. 数学手册 [M]. 2版. 北京: 科学出版社, 1980: 14; 78-97.(Mathematics Teaching and Research Room of China Mining Institute. Mathematics Manual [M]. 2nd ed. Beijing: Science Press, 1980: 14; 78-97.)

[6]沈维道, 蒋智敏, 董钧耕. 工程热力学 [M]. 3版. 北京: 高等教育出版社, 2000: 230-251.(SHEN Wei-dao, JIANG Zhi-min, DONG Jun-geng. Engineering Thermodynamics [M]. 3rd ed. Beijing: Higher Education Press, 2000: 230-251.)

[7]索科洛夫, 津格尔. 喷射器 [M]. 黄秋云, 译. 北京: 科学出版社, 1977: 4-5.(SOKOLOV E я, JINGEER H M . Ejector [M]. HUANG Qiu-yun, transl. Beijing: Science Press, 1997: 4-5.)