基于高阶Radon域的同时震源波场分离
2018-07-09朱翔宇
朱翔宇
1.中国科学院测量与地球物理研究所计算与勘探地球物理研究中心;大地测量与地球动力学国家重点实验室,湖北 武汉 430077;2.中国科学院大学,北京 100049
0 引言
常规地震数据采集,不同震源之间需要足够大的时间间隔以避免相互之间的干扰[1],而同时震源技术突破了常规采集技术的瓶颈。在震源数固定时,同时震源技术可以降低采样时间,提高采集效率;而在相同的采样时间内,通过增加震源密度,可以提升成像质量[2]。并且该技术是宽方位高密度地震数据采集的有效方法,为深层地球物理勘探提供基础。20世纪末,Beasley[3]首次提出同时震源(Simultaneous Sources)这一概念,2008年Berkhout[4]详细介绍了同时震源在采集效率及成像质量上的优势,使得该方法迅速的发展起来。
同时震源数据处理一般可以分为直接偏移[5]和先进行分离然后偏移两种方法。分离类方法将混叠在一起的炮记录进行分离,得到单炮记录,随后可以利用常规的方法进行处理。近几年研究表明分离的方法可以分为两大类即主动分离[6]和被动分离[7]。被动分离[8]一般是从伪分离开始,利用相干滤波进行处理。主动分离[9]是将炮分离看成一个反演问题,利用反演的方法进行处理,因此主动分离方法也可以称之为反演类方法,是将同时震源数据转换到稀疏域,在稀疏域内利用反演进行分离重构。该方法的关键就在于稀疏域的选取。
处理同时震源数据常用的稀疏域有f-k域[10],Seislet域[11],Curvelet域[12],以及 Radon 域[9][13]。由于共检波点域中主炮的数据是相干的,其他炮的数据相对于主炮是不相干的,在Radon域中这两者分别变现为集中的能量点与分散的噪声,借助这个性质可以达到分离的效果,并且Radon变换本身就有去噪能力[14]。
本文利用一种迭代估计的方法进行炮分离,我们首先将共检波点道集数据变换到Radon域,然后利用阈值算子[15]约束模型,通过迭代不断地修正模型,提升分离的信噪比。我们使用的稀疏域为Radon域,但传统的Radon变换正反变换通常会对原始地震数据产生损伤,当地震数据含有较强AVO特征时,地震数据经Radon变换后在振幅上会出现较大误差;高阶Radon变换引入高阶多项式,增强对同相轴保护能力[16],改善分离结果。整形正则化可以加快模型的收敛速度,提高反演效率[11]。通过简单模型和复杂模型数据的处理可以验证本文方法的正确性以及实用性。
1 基于整形正则化的反演分离
海上多源地震可以分为两种激发方式:高密度震源覆盖以及宽范围震源覆盖[17]。其中高密度覆盖时,主震源船正常激发,辅震源船延迟激发,然后主震源船与辅震源船同向行驶,在下一个位置,仍然保持主震源船正常激发,辅震源船延迟激发,依此类推得到混合数据。在这种激发模式下,混合数据在共检波点道集表现出以下特征:主震源反射信号是连续、相干的,而辅震源的反射信号由于时间延迟的存在而不能形成连续、相干的同相轴[18]。本文的分离方法利用上述特征,将共检波点域混合数据进行分离,虽然该方法可以分离多炮混合的数据,但为方便描述以双源混合为例,介绍数据混合的过程,混合数据的表达为:

其中d为混合数据,d1和d2是需要分离的单炮数据,而T代表时间延迟算子。在这种混合方式下,震源1的数据d1是连续相干的,而震源2的数据d2作用了一个时间延迟算子T,变为不连续、不相干的信号。其中时间延迟算子T的表达式为:

方程(2)中F与F-1分别代表傅里叶正反变换,P代表时间延迟的编码方式,其表达式为:

方程(3)中δtn代表时间延迟。对方程(1)左右两边同时乘以时间算子的逆T-1,可以得到:

结合方程(1)、(4)可以得到一个增广方程:

其中
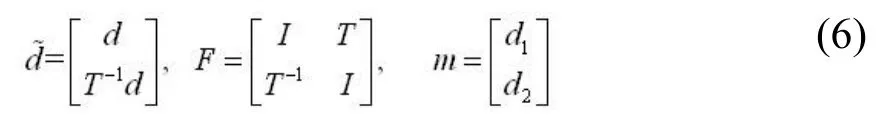
上式中I为单位阵。方程(5)即我们需要求解的方程。
方程(5)可以利用基于整形正则化的迭代方法求解[11](Chenet al,2014),迭代公式可以表示为:

方程(7)中,S是整形算子,与选取的稀疏域有关,B是逆映射算子,B的近似值为二分之一单位阵,即:

方程(5)的解可以表示成L1约束下目标函数的解:

方程(9)中A-1代表变换算子,μ为正则化参数。方程(7)中整形则正则化参数s的表达式为:

结合我们使用的方法,方程(10)中的A、A-1分别代表Radon变换及其逆变换。共检波点道集中,主炮的信号在Radon域是聚焦的能量点,而辅炮则是分散的噪声,Radon变换可以为数据提供良好稀疏性,提高反演的精度。离散Radon变换算子L的表达式为:

方程(11)中ω是频率,qi为慢度,χm为道间距,当n=1时代表线性Radon变换,n=2为抛物Radon变换。频率域离散Radon可以表示为:

D是频率域地震数据,U是Radon域地震数据,L是变换算子。由于L一般不是方阵,传统的方式是通过最小二乘求其广义逆即:

同样给出高阶抛物Radon变换的反变换在频率域的表达式:
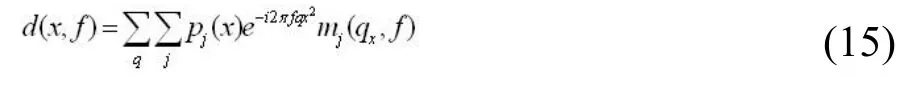
其中pj(x)表示第j阶正交多项式基函数,上述方程改写成矩阵形式:

式中,D(f)为频率域地震数据;LHPRT(f)为高阶抛物Radon变换算子矩阵;变换算子矩阵LHPRT(f)的构造形式如(3-20)式所示:

L0,L1,L2分别为叠加算子,梯度算子与曲率算子,与常规Radon相比,高阶变换的变换算子LHPRT(f)将Radon变化进行延拓,补充振幅的高阶多项式特征,有利于保护同相轴的真振幅[23]。
利用最小二乘方法得到高阶抛物Radon变换的正变换计算公式为:
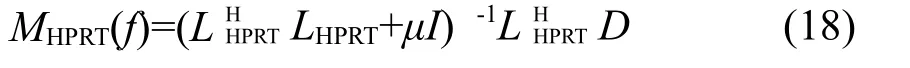
方程(10)中另一个参数Tγ指的是带有输入参数γ的阈值算子,阈值算子是将稀疏域中较大的值保留,较小的值舍去。常用到的阈值算子包含两类:硬阈值和软阈值。硬阈值是将大于阈值的系数保留,小于阈值的系数舍去;软阈值是将大于阈值的系数做收缩处理后保留,小于阈值的参数直接舍去[21]。硬阈值的表达式为:
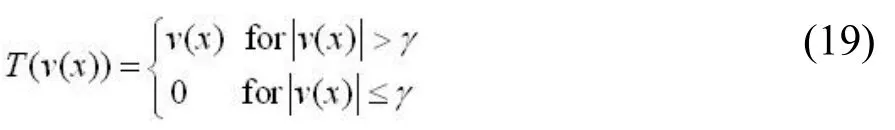
软阈值的表达式为:
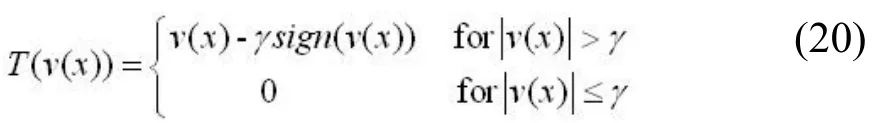
结合后续的算例本文采用硬阈值进行处理。常用的阈值参数γ的选择方式有常数、线性衰减、指数衰减、百分位等方式,不同方式的阈值参数选取会影响迭代的收敛速度[22]。本文采用百分位法。
2 算例分析
2.1 抛物算例
用简单的抛物算例来测试分离方法的有效性,抛物算例包含四条抛物型同相轴,四条同相轴的能量随深度依此减弱,其中图1中(a)为未混合数据,对应公式(1)中的d1,图1中(b)为混合数据,公式(1)对应于d。抛物算例中未混合信号由于没有时间延迟因此是是连续相干的,而混合信号中辅炮的信号由于存在时间延迟变的不连续、不相干。图2、图3均是是利用方程(7)的迭代方法的分离结果,其中图2基于传统的Radon变换,图3基于高阶Radon变换。两种分离方法应用的迭代方程相同,只是稀疏域选取的不同,从分离结果看,两种方法均将主炮信号与辅炮信号进行了分离,但是从残差可以看出,高阶Radon变换对有效信号具有更好的保幅效果,为了评价分离效果,本文利用信噪比进行评估,信噪比的定义为[23]∶

方程(17)中d代表未混合数据,dn代表第n次迭代的结果。
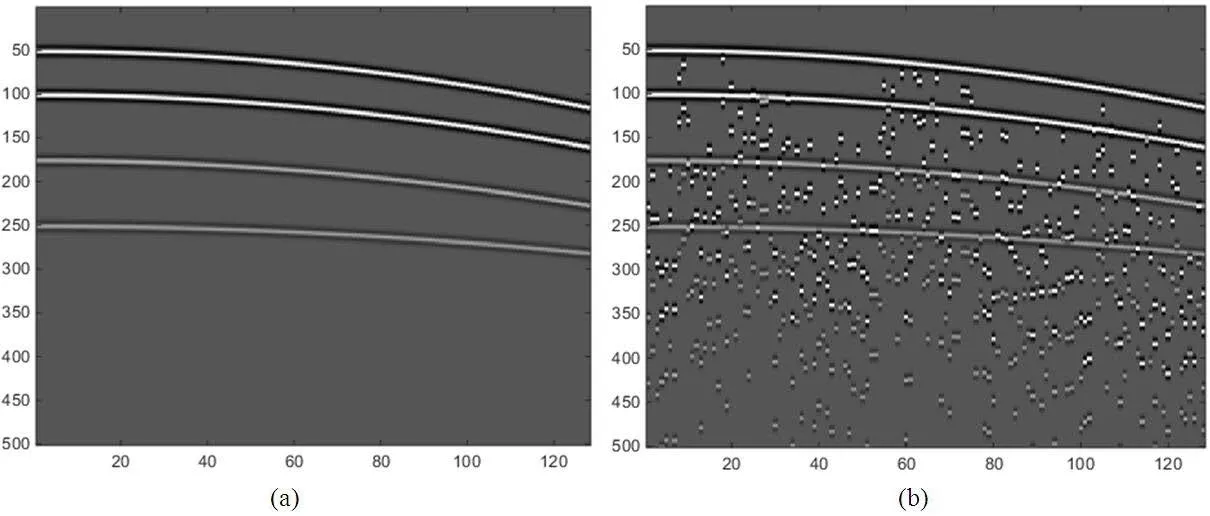
图1 抛物算例Fig.1 Parabolic example
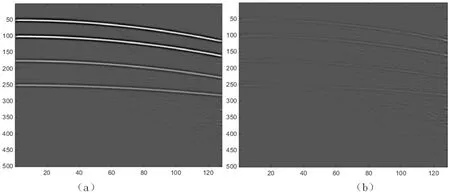
图2 抛物算例传统Radon变换分离结果Fig.2 Separation result of traditional Radon transform for parabolic example
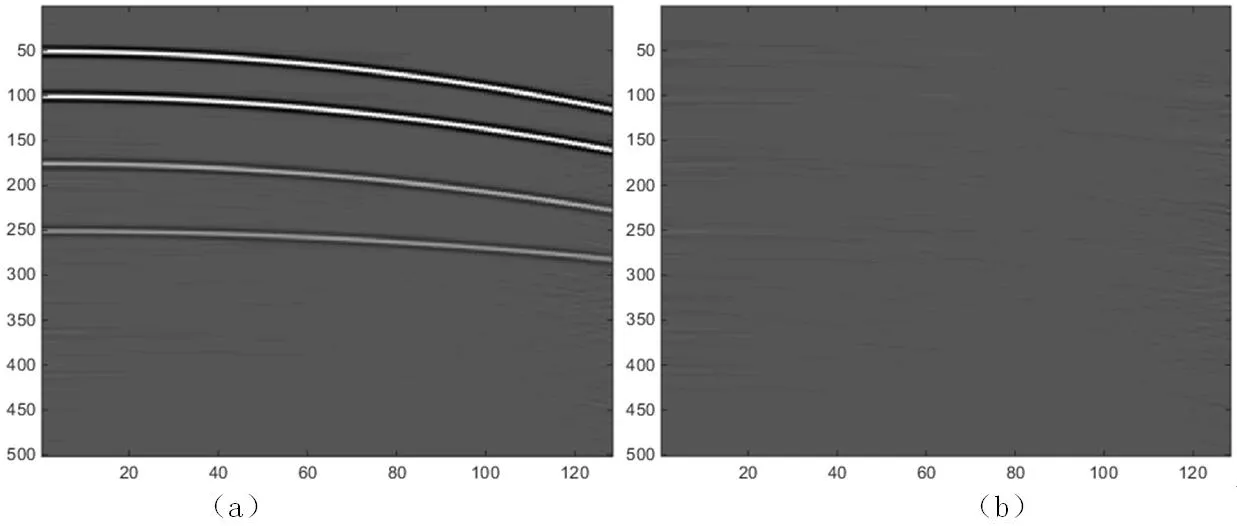
图3 抛物算例高阶Radon变换分离结果Fig.3 Separation result of high order Radon transform for parabolic example
利用方程(17)的信噪比公式分别评估两种方法的分离效果,结果见图4,其中蓝色实线为高阶Radon变换的分离效果,橙色虚线为传统Radon变换的分离效果,两种方法在迭代十五次时基本收敛,且高阶Radon变换的分离结果收敛于25.92 dB,而传统Radon变换的分离结果收敛于20.77 dB。从信噪比来看,高阶Radon变换的分离效果要优于传统Radon变换的分离效果。
2.2 SEAM_2B模型算例
第二个算例,我们用SEAM_2B模型的双源混合数据来模拟实际地震记录。图5是SEAM_2B模型共检波点道集地震记录,其中图5中(a)为未混合数据,对应公式(1)中的d1,图5中(b)为混合数据,对公式(1)应于d。
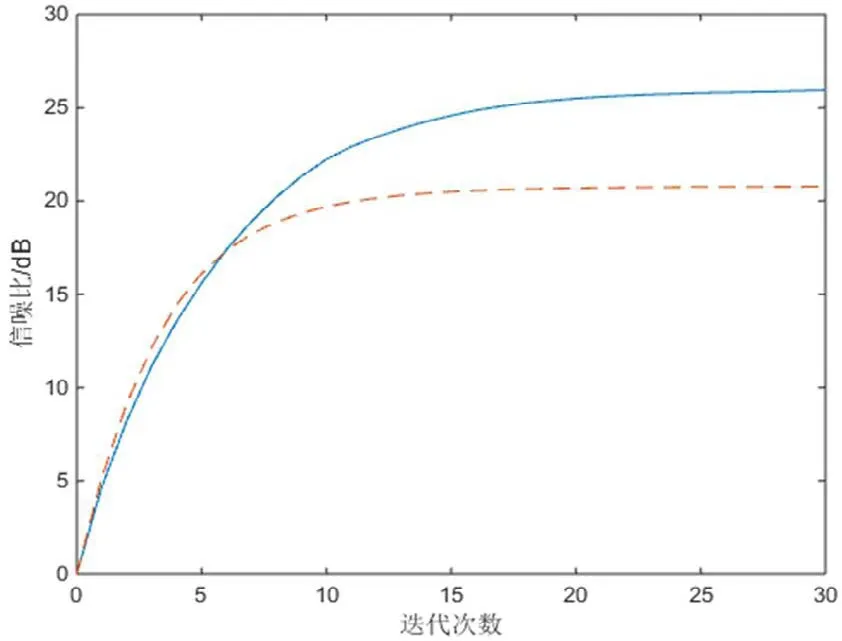
图4 抛物算例两种分离方法信噪比曲线Fig.4 S/N ratio for parabolic example
图5、图6分别是两种方法利用方程(7)的迭代方法的分离结果,其中图5基于传统的Radon变换,图6基于高阶Radon变换。利用方程(17)的信噪比公式评估分别评价分离效果,结果见图7,SEAM_2B模型算例的信噪比也在十五次迭代后基本趋于稳定,高阶Radon变换的分离结果收敛于24dB,而传统Radon变换的分离结果收敛于19.33dB。从信噪比来看,高阶Radon变换的分离效果要优于传统Radon变换的分离效果,并且,高阶Radon变换的分离结果对有效信号有很强的保护效果。
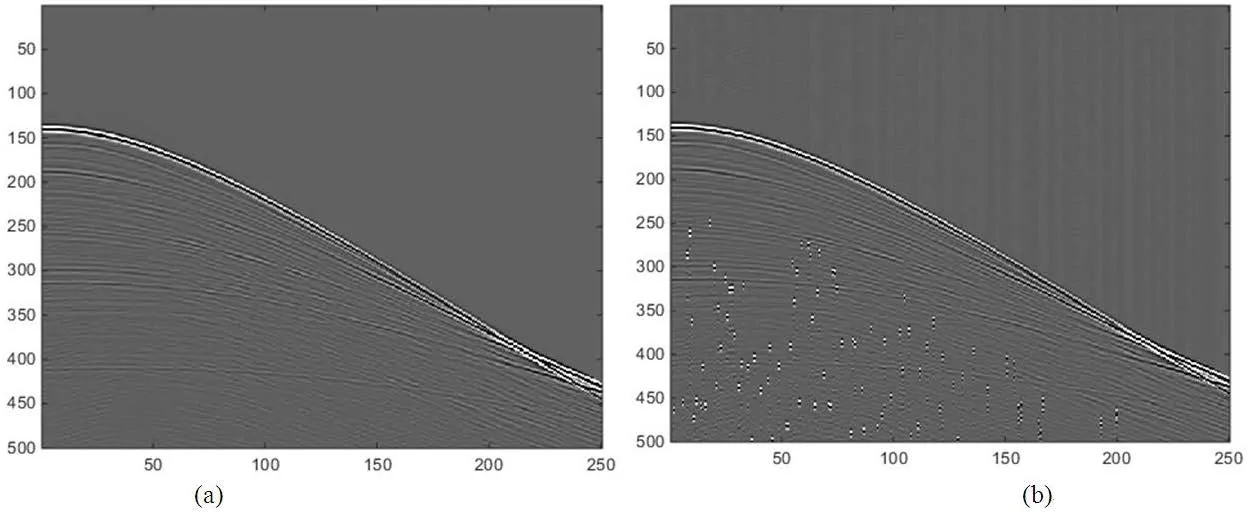
图5 SEAM_2B模型算例Fig.5 SEAM_2B example
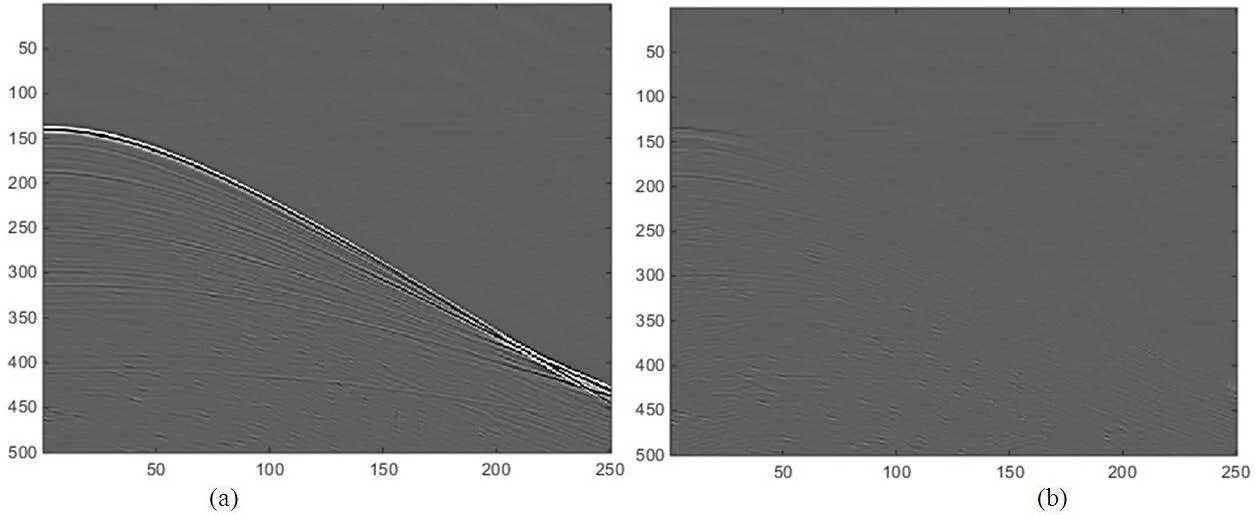
图6 SEAM_2B模型传统Radon变换分离结果Fig.6 Separation result of traditional Radon transform for SEAM_2B example
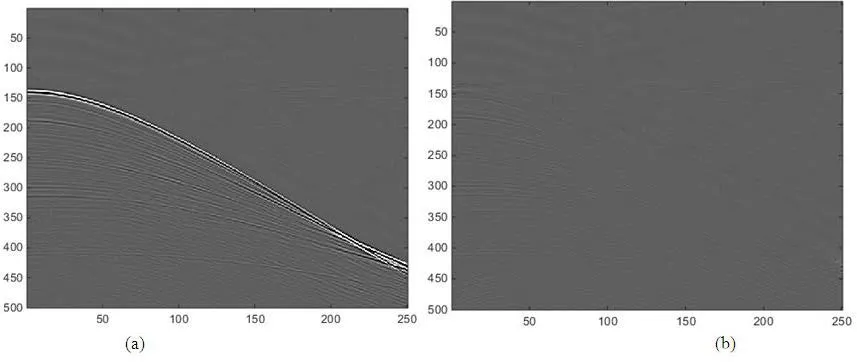
图7 SEAM_2B模型高阶Radon变换分离结果Fig.7 Separation result of high order Radon transform for SEAM_2B example
3 结论
本文通过高阶Radon变换将共检波点域数据转换到稀疏域,利用阈值算子约束模型,通过迭代不断地修正模型,提升分离的信噪比。通过两个模型的试算,可以证明高阶Radon选取的合理性以及迭代分离方法的准确性。并且我们的方法只需要较小的迭代次数就能得到高信噪比的分离结果,说明该算法有很好的实用性。同时对比分析可以发现,两个算例的结果显示高阶Radon变换对有信号具有更好的保幅效果,分离效果也要优于传统Radon变换。
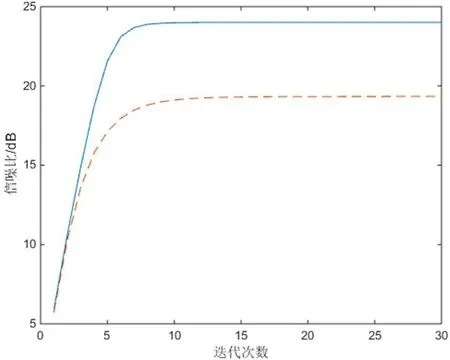
图8 SEAM_2B模型两种分离方法信噪比曲线Fig.8 S/N ratio for SEAM_2B example
[1]Zhou Y, Gao J, Chen W, et al.Seismic Simultaneous Source Separation via Patchwise Sparse Representation[J].IEEE Transactions on Geoscience and Remote Sensing,2016, 54(9)∶5271-5284.
[2]Li C, Mosher C C, Morley L C, et al.Joint source deblending and reconstruction for seismic data[M]//SEG Technical Program Expanded Abstracts 2013.Society of Exploration Geophysicists,2013∶ 82-87.
[3]Beasley C J, Chambers R E, Jiang Z.A new look at simultaneous sources[M]//SEG Technical Program Expanded Abstracts 1998.Society of Exploration Geophysicists, 1998∶133-135.
[4]Berkhout A J.Changing the mindset in seismic data acquisition[J].The Leading Edge,2008, 27(7)∶ 924-938.
[5]Godwin J, Sava P.2010.Simultaneous source imaging by amplitude encoding[J].CWP report,2010, 645.
[6]Moore I.Simultaneous Sources-Continuous Acquisition and Processing for Marine Data[C]//76th EAGE Conference and Exhibition 2014.2014.
[7]Liu Z, Wang B, Specht J, et al.Enhanced adaptive subtraction method for simultaneous source separation[M]//SEG Technical Program Expanded Abstracts 2014.Society of Exploration Geophysicists, 2014∶115-119.
[8]韩立国,谭尘青,吕庆田等.基于迭代去噪的多源地震混合采集数据分离[J].地球物理学报, 2013,56(7)∶2402-2412.
[9]Moore I, Dragoset B, Ommundsen T, et al.Simultaneous source separation using dithered sources[M]//SEG Technical Program Expanded Abstracts 2008.Society of Exploration Geophysicists,2008∶2806-2810.
[10]Mahdad A.Deblending of seismic data[D].TU Delft, Delft University of Technology,2012.
[11]Chen Y, Fomel S, Hu J.Iterative deblending of simultaneoussource seismic data using seislet-domain shaping regularization[J].Geophysics, 2014,79(5)∶ V179-V189.
[12]Zu S, Zhou H, Chen Y, et al.A periodically varying code for improving deblending of simultaneous sources in marine acquisition[J].Geophysics, 2016,81(3)∶ V213-V225.
[13]Sacchi M D.Sparse inversion of the Radon coefficients in the presence of erratic noise with application to simultaneous seismic source processing[C]//Acoustics, Speech and Signal Processing (ICASSP), 2014 IEEE International Conference on.2014∶2386-2389.
[14]唐欢欢,毛伟建.3D高阶抛物Radon变换地震数据保幅重建[J].地球物理学报,2014,57(9)∶2918-2927.
[15]Fomel S.Shaping regularization in geophysical-estimation problems[J].Geophysics, 2007,72(2)∶ R29-R36.
[16]薛亚茹, 唐欢欢, 陈小宏.高阶高分辨率Radon变换地震数据重建方法[J].石油地球物理勘探, 2014, 49(1)∶95-100.
[17]Berkhout A J, Blacquière G, Verschuur D J.The concept of double blending∶ Combining incoherent shooting with incoherent sensing[J].Geophysics, 2009,74(4)∶ A59-A62.
[18]祖绍环,周辉,陈阳康,等.2016.不规则采样的多震源数据整形正则化分离方法[J].石油地球物理勘探,2016,51(2)∶247-253.
[19]巩向博.高精度.Radon变换及其应用研究[D].吉林∶吉林大学,2008.
[20]Aster R C, Borchers B, Thurber C H.Parameter Estimation and Inverse Problems[M].New York∶ Academic Press,2011.
[21]王典,刘财,刘洋,等.基于提升算法和百分位数软阈值的小波去噪技术[J].地球物理学进展,2008,23(4)∶1124-1130.
[22]Yang P, Gao J, Chen W.On analysis-based two-step interpolation methods for randomly sampled seismic data[J].Computers & Geosciences, 2013,51∶ 449-461.
[23]Hennenfent G, Herrmann F J.Seismic denoising with nonuniformly sampled curvelets[J].Computing in Science &Engineering, 2006,8(3)∶ 16-25.
