白荡湖设计洪水计算方法研究

王 万

(安徽省水利水电勘测设计院，安徽 合肥 230088)

白荡湖流域位于长江左岸，西邻菜子湖流域，北与巢湖流域为界，总面积775km2，主要水系有杨市河、钱桥河和罗昌河，3条河汇入白荡湖，经调蓄后通过白荡闸入江。流域地处亚热带季风气候区，流域汛期暴雨集中，雨量大，下游受同期长江洪水位影响，内洪不能自排，出现高水位机率较大，容易形成“关门淹”。

1 设计洪水计算方法

1.1 多元线性回归法

白荡湖流域内均无水文站，湖泊设计洪水计算只能采用间接法。本文拟采用分地形P+Pa～R关系线法和多元线性回归方程两种方法分别计算湖泊的设计洪水，并对计算结果进行对比分析。

多元线性回归方程法主要思路是：考虑流域山区、丘陵区和圩区来水较为复杂，降雨与来水关系及各分区来水如何迭加难以确定，借用其它流域数据缺乏依据。假设关闸期当日湖水位与前1天湖水位、降雨、蒸发是线性关系，确定由湖水位、降雨和蒸发组成的多元线性方程，采用大水年逐日水位、降水和蒸发资料，以各大水年还原总水量为目标函数用最小二乘法优选方程系数。系数确定后，即可确定逐日来水量过程。各年还原总水量以关闸期初、末水位对应的库容差，加上破圩水量确定。

确定各大水年破圩水量对线性回归法结果准确与否非常关键，本次调查了各大水年白荡湖流域圩口溃破情况，但完全未收集到各年圩口溃破的准确日期。因此本次假设破圩均发生在关闸期，破圩水量以关闸期初、末水位读各破圩圩口库容曲线而得。

白荡湖唯一的出口是白荡闸，因此白荡湖关闸期只需利用白荡闸内外水位即可确定。关闸期确定后，破圩水量即可确定。

(1)关闸期选择。利用历史水位和破圩资料初选白荡湖大水年主要为1969、1973、1975、1977、1980、1983、1984、1989、1991、1995、1996、1999、2016年共13年。

各年关闸期选用原则：①包含该年汛期湖水位低于江水位最长时段，②该时段内应该包含了该年最高湖水位出现的时段，③所有圩口破圩时间均发生在该段时间内，④采用关闸期起始日期至最高湖水位出现日期(认为该年破圩均在该水位之前发生)之间的时段作为该年关闸期的计算时段。统计过程中发现部分年份关闸期时段分散，但中间间隔时间较短，本文为保证一定长度的关闸期，以便该年所有破圩都是在这一时间段内，计算采用时段对其进行的衔接，至于中间衔接段开闸抢排的水量，采用了白荡闸对应的江湖水位进行估算还原。

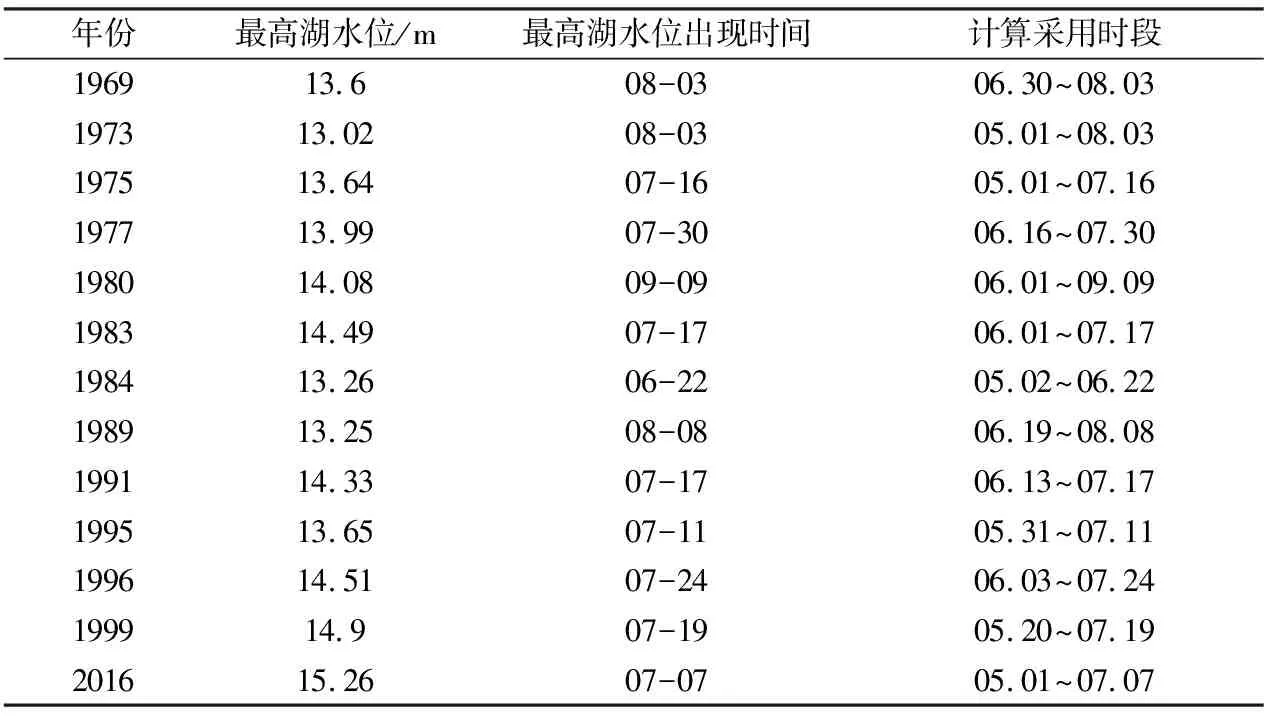
表1 白荡湖大水年关闸期统计表

注：1954年白荡闸上下无水位数据以及详细的破圩资料，故无法统计

(2)破圩水量还原及关闸期总来水量确定。本次收集了各大水年破圩面积资料，但未完全收集到破圩具体时间，因此破圩水量采用关闸期最高水位查各破圩圩口的库容曲线而得。关闸期总来水量为关闸期末水位、初水位对应的白荡湖库容差，加上破圩水量确定。

(3)多元线性回归计算成果。关闸期间湖水位变化过程实际就是关闸期间雨量、蒸发等因子综合作用过程，而湖水位的时段增量过程就是入湖径流量的变化过程，因而可以从分析资料较完整的湖水位过程入手，来确定该流域的次降雨径流关系。本次选用了不同日期的降雨、蒸发、水位作为回归因子，对典型年进行了回归计算，采用的回归方程形式如下：

Ht=Ht-1+A+B.Pt-1+C.Pt-1.Et-1

其中, A、B、C为参数；Ht为第t日湖水位，m；Ht-1为第t-1日湖水位，m；Pt-1为第t-1日降雨量，mm； Et-1为第t-1日E601观测蒸发量，mm。

对回归方程的参数A、B、C进行优选，以关闸期还原产水量为目标函数，用最小二乘法优选出使总体产水量误差最小的参数。优选后系数为：A=-0.01769，B=0.00977，C=0.00004。将系数带入回归方程中，得到各个典型年最终模拟结果如表2所列。根据以上结果可以看出在13个典型年中年水量相对误差除1989年较大外，其余年份误差均较小，故多元线性回归拟合程度较好。

表2 白荡湖线性回归方程模拟计算表

1.2 P+Pa～R关系线法

鉴于流域内山丘、圩区和湖具有，来水复杂，采取分地形借用相似流域降雨径流关系曲线，根据流域以往规划成果，山区借用黄栗树站次降雨径流关系曲线，丘陵站选用桃溪站次降雨径流关系曲线、平原圩区借用江苏太湖区旱地次降雨径流关系线、湖面采用降雨减蒸发的办法进行计算。白荡湖流域全流域面积775km2，其中山丘区面积576km2(山区169km2，丘陵407km2)，平原圩区面积142km2，湖泊面积57km2。

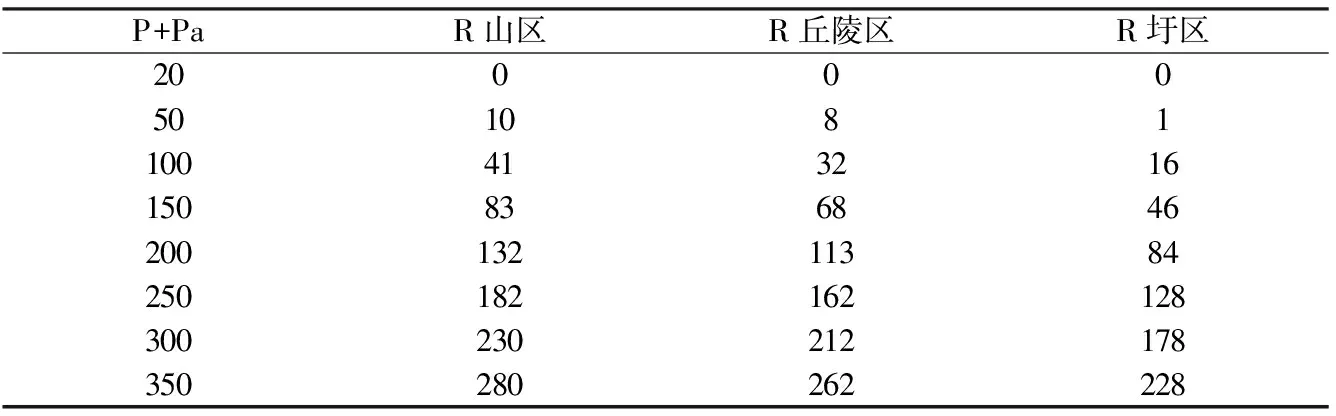
表3 山丘圩P+Pa～R关系曲线 mm

本文为了便于将两种计算方法计算结果进行对比分析，各典型年P+Pa～R关系线法计算时长采用与线性回归法一致，均为统计的关闸期时段。

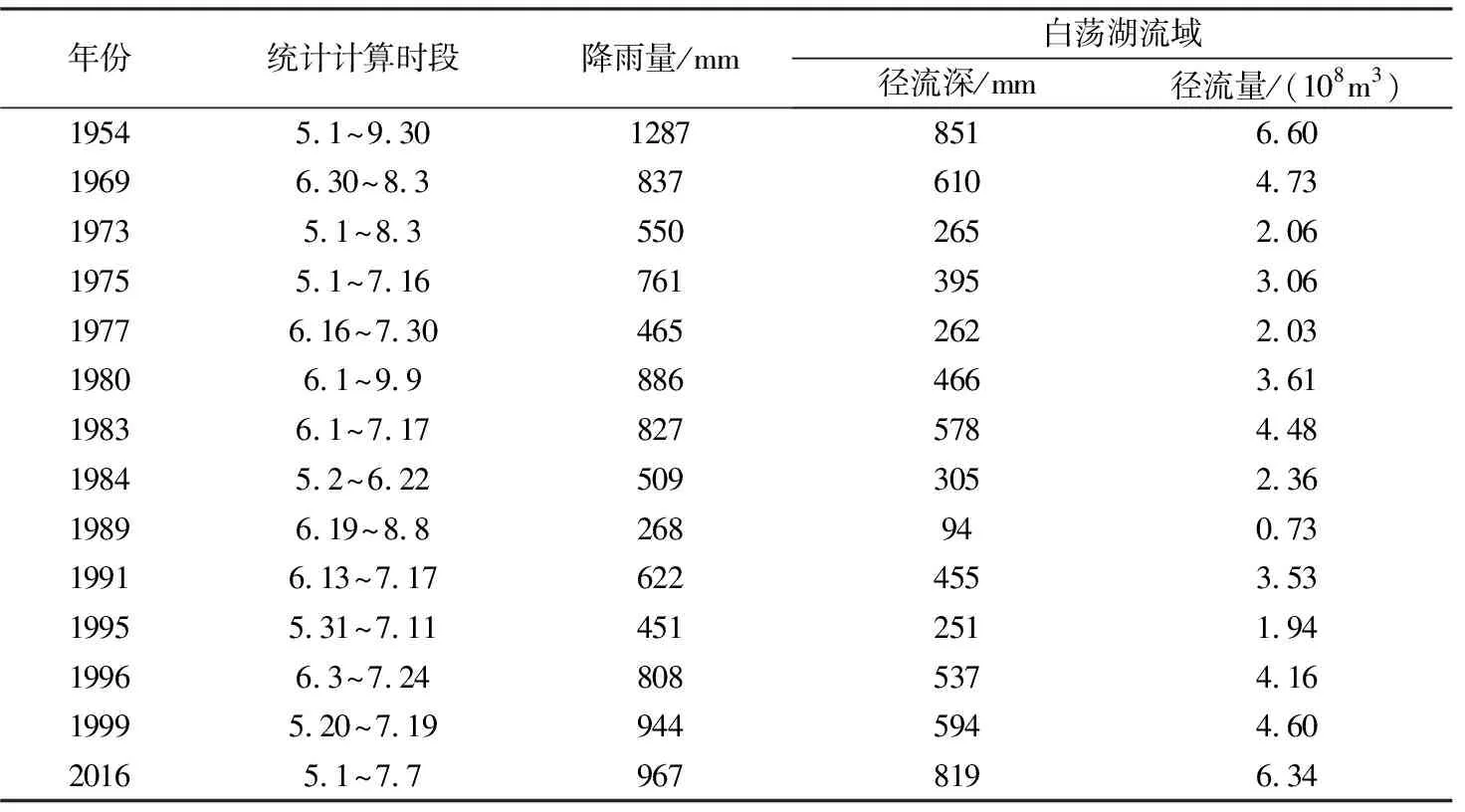
表4 白荡湖流域山丘区P+Pa～R典型年计算结果

2.3 2种计算方法计算结果对比分析

通过对2种计算方法结果得到的洪量进行对比分析可知，2种计算结果基本一致，但总体在1969、1983、1996、1999和2016年这样的大水年差别较小，2种方法差别均在10%以内，但在1977、1984、1989等年份差别较大。鉴于白荡湖流域整体防洪标准都在20年1遇及以上，故2种方法在白荡湖流域设计洪水计算中效果较好。

表5 白荡湖流域山丘区P+Pa～R典型年计算结果

2 结论与建议

本文分别采用线性回归法和P+Pa～R分别对流域典型年洪水进行了计算，经比较分析，2种方法对大水年份相对误差较小，对较小的洪水年份相对误差较大。同时针对2种计算方法的特点可知，线性回归法主要对总水量进行控制，P+Pa～R法利用逐日降雨计算洪水过程，对过程的控制较好，但对总水量缺乏控制，因此从控制来水量和来水过程综合考虑，建议可采用线性回归法计算的总水量控制总来水量，并用P+Pa～R法计算的来水过程比例分配至逐日过程。

[参 考 文 献]

[1] 唐红兵,陈昌才.枞阳县白荡湖、陈瑶湖流域综合规划报告[R].安徽省水利水电勘测设计院，2010.

[2] 王万，唐红兵.白荡湖流域治理规划[R].安徽省水利水电勘测设计院，2017.

[3] 叶守泽.水文水利计算[M]. 北京：中国电力出版社，1991.