防腐镀层对引信软带弯矩的影响

王永亮，王雨时，闻 泉，张志彪

(南京理工大学机械工程学院，江苏 南京 210094)

0 引言

软带机构是引信的一种典型延迟解除保险机构，同时也是离心保险机构，广泛应用于旋转炮弹引信，尤其是小口径旋转炮弹引信。国内引信软带通常用紫铜制成，料条厚度约为0.14～0.18 mm，带长约为100～500 mm[1]。为了保证其长期储存寿命，需对其进行表面防腐处理。文献[1]介绍了引信紫铜软带的常用表面防腐处理层是锡镀层，即Ep·Sn7，其镀层厚度约为0.007 mm[2]。

金属镀层在构成防腐保护层的同时还会影响引信软带抗力即弯矩，从而影响到机构解除保险的正确性。由于镀层不匀或超厚所引起的产品瞎火率偏高的质量问题在历史上炮引-21和炮引-23引信批量生产时时有发生。文献[3]分析了镀层材料及厚度与引信弹簧抗力的关系，对于同一镀层材料，引信弹簧抗力是随着镀层厚度的增大而增大的；对于不同镀层材料，镀层材料的屈服强度是影响引信弹簧抗力的主要因素。尽管前人在镀层对构件机械性能的影响方面做了一些研究，但目前尚未见有文献揭示引信软带镀后抗力即弯矩变化机理以及对引信软带生产质量控制的影响。本文针对此问题，提出了基于塑性力学理论的镀后软带及其镀层弯矩的计算方法。

1 传统无镀层软带弯矩理论分析[4]

如图1所示，当引信软带无防腐镀层时，软带弯曲时曲率半径远大于软带厚度，因此可以认为软带横截面的形心与横截面的中性轴是重合的。

假设软带弯曲过程中，在软带横截面内与软带中性轴距离为y的一纤维CD被拉长到C′D′，则软带应变为

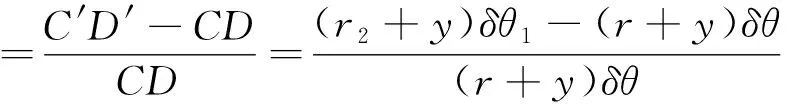
(1)

式(1)中，r表示软带曲率半径，r2表示经过端部弯矩作用的曲率半径，软带打开过程中，恒有r2>r。

由于在中性轴上，AB=A′B′，所以，rδθ=r2δθ1。化简得

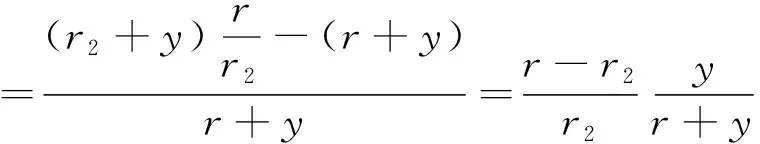
(2)

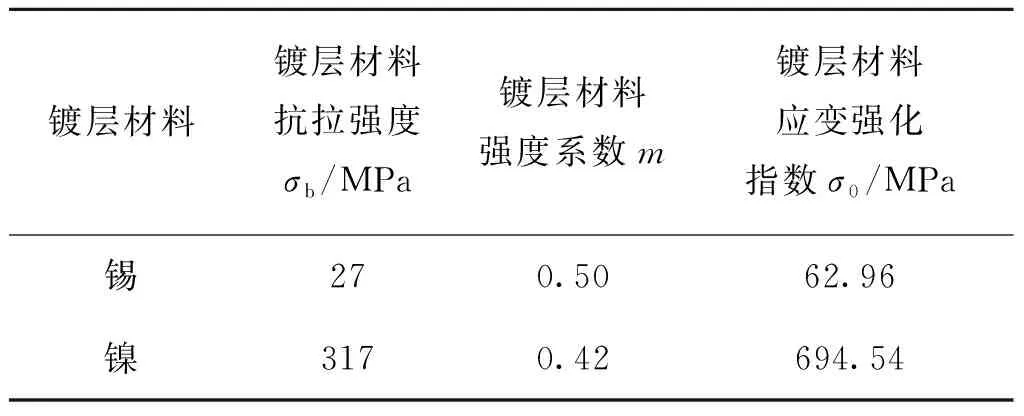
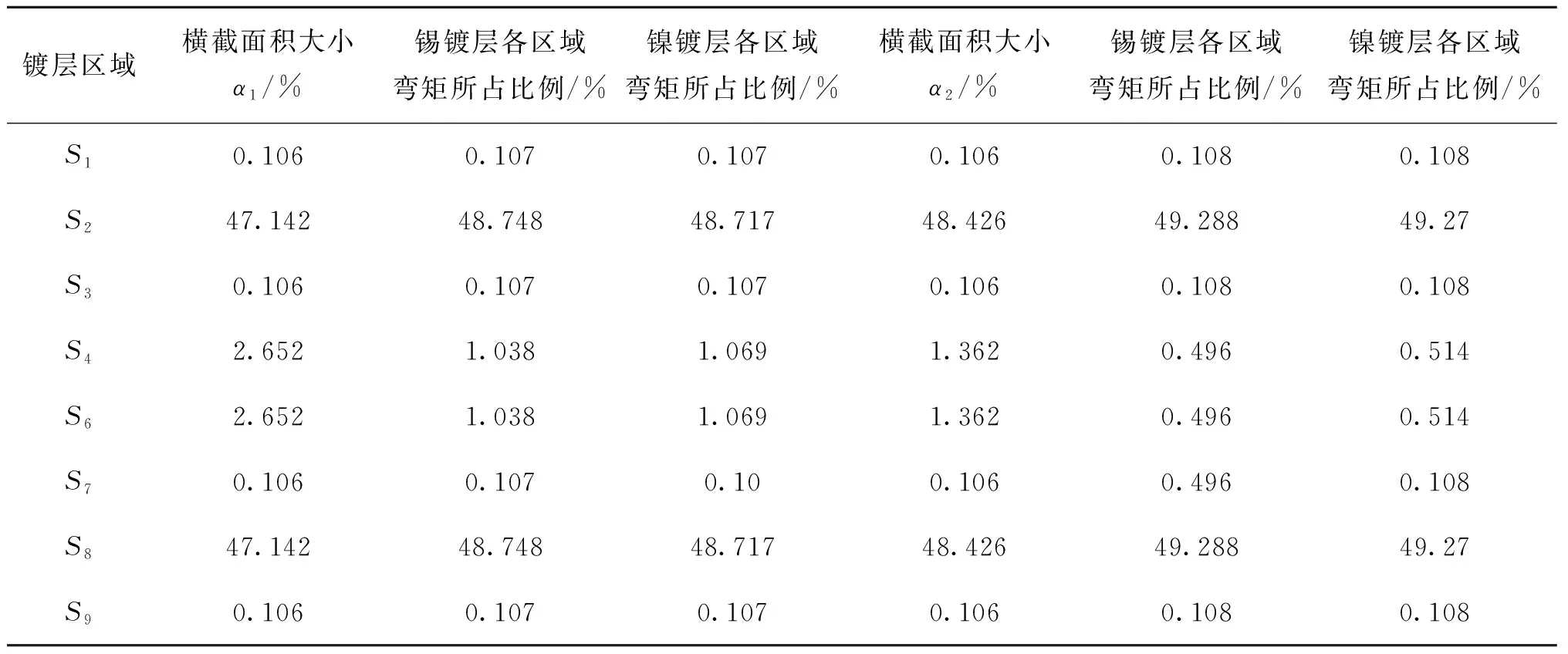
由于y<

(3)

故按照塑性理论[5]软带有应力

(4)

则软带弯矩[6]

(5)

式(5)中，h为软带宽度，σ0为软带材料强度系数，r为软带曲率半径，r2为端部弯矩作用后的曲率半径，m为软带材料应变强化指数，c为软带带条的厚度。

2 镀后软带及其镀层弯矩理论分析

2.1 基于塑性力学理论推导

软带外表面都有镀层。从横截面上看，可将其分为上镀层、下镀层以及左、右镀层然后分别进行弯矩分析。

软带弯曲时，其镀层也会产生相应的弯曲。其弯矩分析与软带相似，即也可以假设弯曲后镀层中性轴与截面的形心仍是重合的。

如图2所示，软带弯曲时曲率半径远大于软带及其镀层厚度，因此仍可以认为软带横截面的形心与横截面的中性轴是重合的。

由于y同样是远小于r的，所以镀层应变为

故按照塑性理论[5]镀层有应力

式中,σ0′为镀层材料强度系数，m1为镀层材料应变强化指数。

镀后，软带及镀层截面如图3所示，其曲率半径为r，在端部弯矩作用后，其曲率半径为r2。

由S1、S2和S3构成的上方镀层的厚度为d，宽度为h+2d，则上方镀层的弯矩大小(不考虑正负号)[6]为：

(6)

式(6)中,h为软带宽度，d为镀层的厚度。

由S7、S8和S9构成的下方镀层弯矩M2与S1、S2和S3构成的上方镀层弯矩M1相同。

由S4和S6构成的左、右镀层宽度与软带带条的厚度相同，均为c，而其厚度为d。

则左、右镀层的合弯矩大小(不考虑正负)[6]为：

(7)

因此镀后总弯矩为

M′=M+M1+M2+M3=

(8)

引信软带镀后的弯矩变化率为

(9)

2.2 具体算例及分析

2.2.1公式验证

以炮引-1引信软带为例，其主要结构参数如表1所列。

查阅文献[4]炮引-1引信软带解除保险过程中的几何学分析数值计算结果与带桥变化过程的数值，得知炮引-1引信软带打开长度为125.55 mm时，软带外圈曲率半径r=3.01 mm，而软带打开后的曲率半径r2=4.42 mm。

Tab.1 Main structural parameters of fuze unwinding ribbon of PY-1[4]

带条宽度h/mm带条厚度c/mm软带材料强度系数σ0/MPa软带材料应变强化指数m3.2-0.080.18-0.02468.840.48

假设引信软带材料与镀层材料均为紫铜，分别用式(5)和式(8)计算炮引-1引信软带在镀层厚度d=0.007 mm时的镀后软带弯矩，结果均为1.27 N·mm。即假设引信软带材料与镀层材料为同一种材料时，式(5)在引信软带宽度为h+2d、厚度为c+2d的条件下计算得出的结果与式(8)在引信软带宽度为h、厚度为c且镀层厚度为d的条件下计算得出的结果一致，则式(8)的正确性得到了验证。

2.2.2镀层厚度对软带弯矩的影响

查阅文献[2]得引信软带的镀锡标准和镀镍标准与镀层厚度的关系见表2。

表2 镀锡和镀镍标准及镀层厚度

Tab.2 Tin and nickel plating standard and coating thickness

镀锡标准厚度范围/μm选取厚度d/μm镀镍标准厚度范围/μm选取厚度d/μmEp·Sn44～75.50EP·Ni55～86.50Ep·Sn77～129.50EP·Ni88～1210.00Ep·Sn1212～1815.00EP·Ni1212～1815.00

文献[7]给出金属板料强度系数σ0与材料应变强化指数m之间的关系式为:

(10)

式(10)中，σb为抗拉强度，e为自然常数。

查阅文献[8]和文献[9]得到锡和镍的抗拉强度σb和应变强化指数m1的值，代入式(10)计算出其强度系数σ0′，如表3所列。

将上述参数代入式(5)、式(8)和式(9)计算炮引-1引信软带在表2所列不同镀锡标准下电镀前后的弯矩变化率ΔM，分别为2.00%、3.55%和5.87%。镀后引信软带弯矩有一定变化，是随着镀层厚度的增大而增大的。

表3 引信软带镀层的强度系数和应变强化系数

Tab.3 Strength factor and strain hardening exponent of coating of fuze unwinding ribbon

镀层材料镀层材料抗拉强度σb/MPa镀层材料强度系数m镀层材料应变强化指数σ0/MPa锡270.5062.96镍3170.42694.54

2.2.3镀层材料对软带弯矩的影响

文献[4]介绍了铜质引信软带表面涂覆层除了常用的锡镀层之外，还可采用镍镀层。研究不同镀层材料对引信软带弯矩的影响也很有必要。查阅文献[2]得引信软带的镀镍标准与镀层厚度的关系也列入了表2。

将表2参数代入式(5)、式(8)和式(9)计算引信软带分别在镀锡和镀镍的标准下的弯矩变化率ΔM，结果列入表4。表中两列弯矩变化率ΔM1和ΔM2数值，分别对应炮引-1引信软带和在炮引-1引信软带基础上软带厚度减半的情形。

表4 软带在不同电镀标准下的弯矩变化率ΔM

Tab.4 The bending moment change rate of unwinding ribbon under different plating standards

电镀锡选取厚度d/μmΔM1/%ΔM2/%电镀镍选取厚度d/μmΔM1/%ΔM2/%Ep·Sn45.502.004.04EP·Ni56.5037.8681.94Ep·Sn79.503.557.49Ep·Ni810.0059.90132.93Ep·Sn1215.005.8712.85Ep·Ni1215.0093.47214.39

由表4得在镀层厚度相同的情况下，对于上述2种镀层材料，引信软带镀镍后软带弯矩变化率较大，而镀锡后软带弯矩变化率较小，镀层材料强度系数和应变强化指数是影响软带弯矩变化率的主要因素。

2.2.4各镀层区域对软带弯矩的影响

以炮引-1引信软带为例，在镀层材料为锡、镀层厚度d=0.007 mm、采用表3引信软带参数时，计算图3各镀层区域的弯矩占总镀层弯矩的比例，

如表5所列。表中两列横截面积大小α1和α2数值分别对应炮引-1引信软带和在炮引-1引信软带基础上软带厚度减半的情形。

由表5得引信软带弯矩受镀层S2和S8区域的影响最大，镀层S4和S6区域对其影响其次，其余区域的镀层对其影响甚微。原因主要是镀层S2和S8区域的横截面积最大。不同区域镀层产生的弯矩影响与其横截面积大小密切相关。

表5 各镀层区域所占比例

Tab.5 Proportion of each coating area

镀层区域横截面积大小α1/%锡镀层各区域弯矩所占比例/%镍镀层各区域弯矩所占比例/%横截面积大小α2/%锡镀层各区域弯矩所占比例/%镍镀层各区域弯矩所占比例/%S10.1060.1070.1070.1060.1080.108S247.14248.74848.71748.42649.28849.27S30.1060.1070.1070.1060.1080.108S42.6521.0381.0691.3620.4960.514S62.6521.0381.0691.3620.4960.514S70.1060.1070.100.1060.4960.108S847.14248.74848.71748.42649.28849.27S90.1060.1070.1070.1060.1080.108

3 仿真验证

由于软带打开过程是高速旋转下的动态过程，难以进行试验观测，所以拟通过有限元仿真说明理论分析结果的可信性。用有限元软件ANSYS Workbench数值模拟引信软带在镀锡前后的弯矩。软带采用炮引-1引信软带，镀锡标准采用Ep·Sn4，镀层厚度d=0.005 5 mm，引信软带材料参数和镀层材料参数与理论推导部分的参数相同。

图4(a)和图4(b)分别为引信软带镀锡前后未展开形成带桥时的计算机辅助工程CAE模型，此时r=3.01 mm、r2=4.42 mm。图5(a)和图5(b)分别为用有限元软件ANSYS Workbench模拟引信软带镀锡前后展开形成带桥即r=3.01 mm、r2=4.42 mm时的模拟结果。

由ANSYS Workbench数值模拟结果可得引信软带镀锡前后由未展开状态到带桥状态产生的弯矩不同，镀锡前后引信引信软带由r=3.01 mm到展开形成带桥r2=4.42 mm时弯矩变化率为2.23%，与理论推导结果2.00%基本一致，说明理论分析结果是可信的。

4 结论

本文提出了基于塑性力学理论的镀后软带及其镀层弯矩的计算方法。该方法建立了防腐镀层材料和厚度与引信软带弯矩的计算公式，揭示了引信软带镀前和镀后弯矩的变化情况。仿真实验结果与理论推导分析结果基本一致，验证了其可信性。分析结果表明：对于同一种镀层材料，引信软带弯矩是随着镀层的厚度增大而增大的，对于0.18 mm厚的紫铜软带镀覆0.007 mm厚的锡镀层后，弯矩约增大2.65%；对于不同种镀层材料，镀层材料的强度系数和应变强化指数是影响引信软带弯矩大小的主要因素，镀镍后引信软带弯矩比镀锡后引信软带弯矩变化更大；对于同一镀层不同区域，所产生的影响不同，引信软带料条正反面区域镀层影响最大，不同区域镀层产生的弯矩影响与其横截面积大小有关。这些结论可以为引信软带设计计算以及引信软带生产时控制软带弯矩提供理论依据，例如在引信软带设计时可以预留出镀层引起的弯矩增加量，从而确保引信软带在解除保险时能可靠甩开。

由此看来，软带表面防腐镀层对软带打开弯矩有影响，并且镍镀层影响很大。因而引信软带表面防腐处理不宜选择镍镀层，最好能选择“无厚度”的钝化处理。

参考文献:

[1]GJB/Z 135-2002引信工程设计手册[S]. 北京：人民解放军总装备部，2002.

[2]GJB/Z 594A-2000金属镀覆层和化学覆盖层选择原则与厚度系列[S]. 北京：国防科学技术工业委员会，2000.

[3]刘荔斌，王雨时，闻泉. 镀层对引信弹簧抗力的影响[J]. 兵工学报，2015(11)：2087-2092.

[4]王雨时. 引信软带技术原理与设计[M]. 沈阳：沈阳工业学院，1998：43-45.

[5]吴诗惇. 金属超塑性变形理论[M]. 北京：国防工业出版社，1997：11-15.

[6]余同希，章亮炽. 塑性弯曲理论及其应用[M]. 北京：科学出版社，1992：10-16.

[7]孙东继，林建平，刘瑞同，等. 金属板料幂指型硬化模型应变强化系数K值研究[J]. 塑性工程学报，2009(1)：149-152.

[8]钟延志，曹占伦，刘东明. 新编常用金属材料手册[M]. 北京：人民邮电出版社，2008：898-929.

[9]王燕文，何景素. 金属的超塑性[M]. 北京：科学出版社，1986：303-311.