等距离大圆航线设计方法

朱银兵， 李 豹， 曹可劲

(海军工程大学 电气工程学院，武汉 430033)

在航海上，航线设计通常有恒向线、大圆航线和混合航线等3种方法，其中恒向线较为常用，但当船舶所经过区域的纬度较高、横跨经度差较大时，采用大圆航线设计的航程往往更经济。当前对大圆航线的研究比较多，但主要集中在等经差大圆航线[1-9]设计方法上，该方法已在航海上得到广泛应用。此外，文献[7]和文献[10]涉及等距离的大圆航线设计方法，但文献[7]并未对该方法进行具体描述，而文献[10]只给出一种近似计算方法，在实际应用中存在一定的局限性。研究分析结果表明，现有等距离大圆航线设计方法在高纬度地区、起始点与到达点的纬度接近等情况下的设计结果不可信，且在某些特殊情况下求解最后一段航向时起始航向角计算可能出现奇异现象。为解决上述问题，本文从球面三角形基本原理出发，推导等距离大圆航线的设计过程，从根本上解决上述问题，使算法具有普遍意义上的广泛适用性，从而具备推广应用价值。

1 等距离大圆航线设计算法

文献[10]给出的方法存在不足的根源是在计算分段之后的各中间点的地理坐标时，需依据经度差和纬度差符号确定迭代过程中纬度变化量Δφ的符号；同时，后一级中间点的计算是由前一级中间点计算的结果推导得到的，导致计算过程中的误差存在传导效应，使得起始航向角计算可能出现奇异现象。为从根本上解决该问题，本文基于球面三角形特性，从原理上推导等距离大圆航线设计方法。

图1为等距离大圆航线设计算法，假设航线起始点和目标点的地理坐标分别为点A(φ1,λ1)和点B(φ2,λ2)，根据球面三角余弦定理可得A、B两点间的大圆弧距为

S=arccos(sinφ1sinφ2+cosφ1cosφ2cosΔλ)

(1)

式(1)中：S为大圆总弧距；点A与点B间的经度差为Δλ=λ2-λ1。根据等距离分段基本要求，可将大圆弧距S按一定弧距长度d划分为n段，有

(2)

根据球面三角形特性，可得起点A到目标点B的起始航向角C满足

(3)

式(3)中：C可根据以下规则确定，即

(4)

根据上述假设，以弧长d为基准进行分段，中间点可表示为Di(φi,λi)，其中i=1,2,…，n-1，且Ai为起始点A与中间点Di之间的经度差，Si(Si=id)为起始点A至中间点Di的弧距，P为极点，则在球面三角形PDiA中有

sinφi=sinφ1cossi+cosφ1sinsicosC

(5)

因此中间点Di的纬度为

φi=arcsin(sinφ1cossi+cosφ1sinsicosC)

(6)

由于

cossi=sinφ1sinφi+cosφ1cosφicosAi

(7)

因此有

(8)

可得中间点Di的经度为

λi=λ1+Ai

(9)

2 算法性能分析

为检验本文设计算法的针对性和广泛适用性，结合5个案例与文献[10]进行对比分析。

2.1 一般航线设计

为分析本文方法对一般航线设计的适用性，设定航线起点为(28°50′.00S，32°00′.00E)，目标点为(6°30′.00S，105°00′.00E)，采用2种方法所得一般航线设计结果见表1。

表1 采用2种方法所得一般航线设计结果

在该算例中，根据式(1)计算大圆航线距离为4 319.80 n mile，采用本文方法所得设计结果超出7.33 n mile，采用文献[10]方法所得设计结果超出31.96 n mile，二者差别不大，都实现了航线的正确规划，即本文方法同样适用于一般航线的设计。

2.2 高纬度区域航线设计误差分析

为检验本文方法在高纬度区域航线设计的适应性，设定航线起点为(75°30′.00S，030° 05′.00 W)，目标点为(56°00′.00S，151°00′.00 W)，采用2种方法所得高串度区域航线设计结果见表2。

根据式(1)计算大圆航线距离为2 583.32 n mile，采用本文方法所得航线设计结果超出44.4 n mile，属正常现象；采用文献[10]方法所得航线设计结果的倒数第2个点与目标点之间的距离明显异常，导致航线累计距离超出1 323.5 n mile，这是由于在高纬度地区，起始点和目标点纬度均较高，且纬度相差不大，使得大圆航线中间航点的纬度按照先增大后减小的趋势变化。文献[10]根据起始点和目标点的纬度大小变化来确定迭代过程中的纬度变化量Δφi+1=dcosCi(其中：Δφi+1为第i+1个中间点的纬度迭代变化量；Ci为由第i个中间点计算得到的起始航向角)；该算例采用该近似计算必然导致中间航点的纬度逐渐减小到56°，设计的过程必将逐步偏离大圆航线，从而导致设计的结果不可信，设计的总距离产生突变。

表2 采用2种方法所得高纬度区域航线设计结果

2.3 起点和目标点纬度相近误差分析

为检验本文方法在纬度差较小情况下的适用性，设定航线起点坐标为(25°30′.00N，121°05′.00E)，目标点坐标为(22°00′.00N，151°00′.00W)，采用2种方法所得纬度相近航线设计结果见表3。

表3 采用2种方法所得纬度相近航线设计结果

根据式(1)计算大圆距离为4 736.90 n mile，采用本文提出的方法得到的航线设计结果超出12.7 n mile，正常；采用文献[10]中的方法得到的距离超出1 113.6 n mile，且在到达目标点时需大角度转向，明显异常。设计结果不可信的原因是该算例中起始点和目标点的纬度接近，大圆航线中间航点的纬度会按照先增大后减小的趋势变化，而文献[10]的近似处理会导致中间点纬度一直减小，从而偏离正确航线。

2.4 航向奇异现象分析

为检验本文方法的优越性，设定航线起点坐标为(34°40′.00N，140°00′.00E)，目标点坐标为(44°40′.00N，163°40′.00E)，采用2种方法所得航线设计结果见表4。

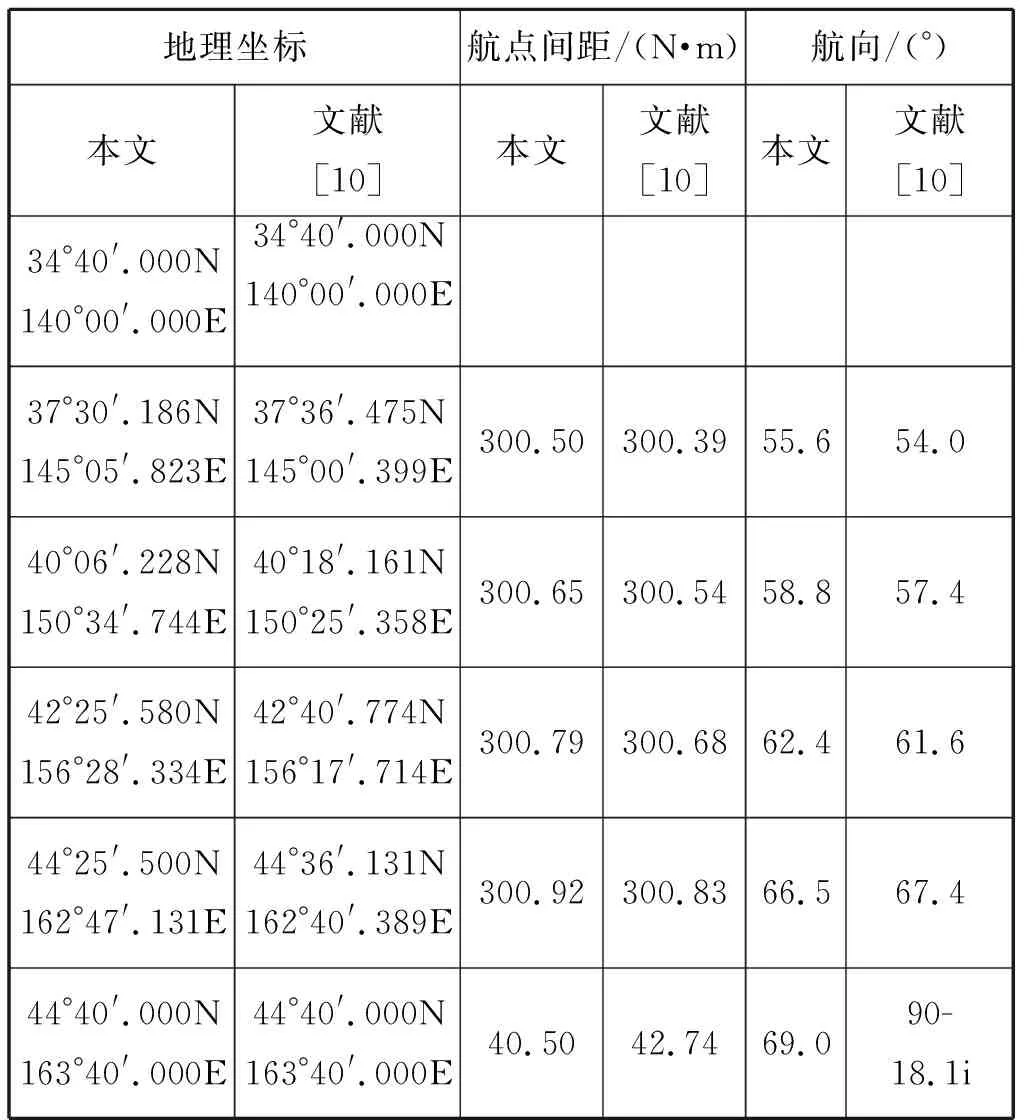
表4 采用2种方法所得航线设计结果

在该算例中，根据式(1)计算大圆总距离为1 240.37 n mile，采用本文提出的方法得到的航线设计结果超出约3 n mile，而采用文献[10]中的方法得到的距离也仅超出4.8 n mile。从距离上看，二者差别不大：文献[10]中的方法由于采用了近似计算，中间点的位置计算误差对后续中间点的计算存在误差积累效应，当积累到足够大时，将导致其中某个中间点在计算其起始航向时，起始航向的正弦绝对值>1，即|sinCi|>1，从而导致中间点的起始航向产生奇异值；而本文方法则以已知的起始点为基准进行计算，从源头上避免了中间点计算过程中的误差积累问题，从而有效避免了航向计算的奇异值问题出现。

2.5 极区附近航线设计

为检验本文方法在极区附近的适用性，设定航线起点为(57°30′.00N，000° 00′.00E)，目标点为(78° 00′.00N，170°00′.00E)，采用本文方法所得等距离大圆航线设计结果见表5。

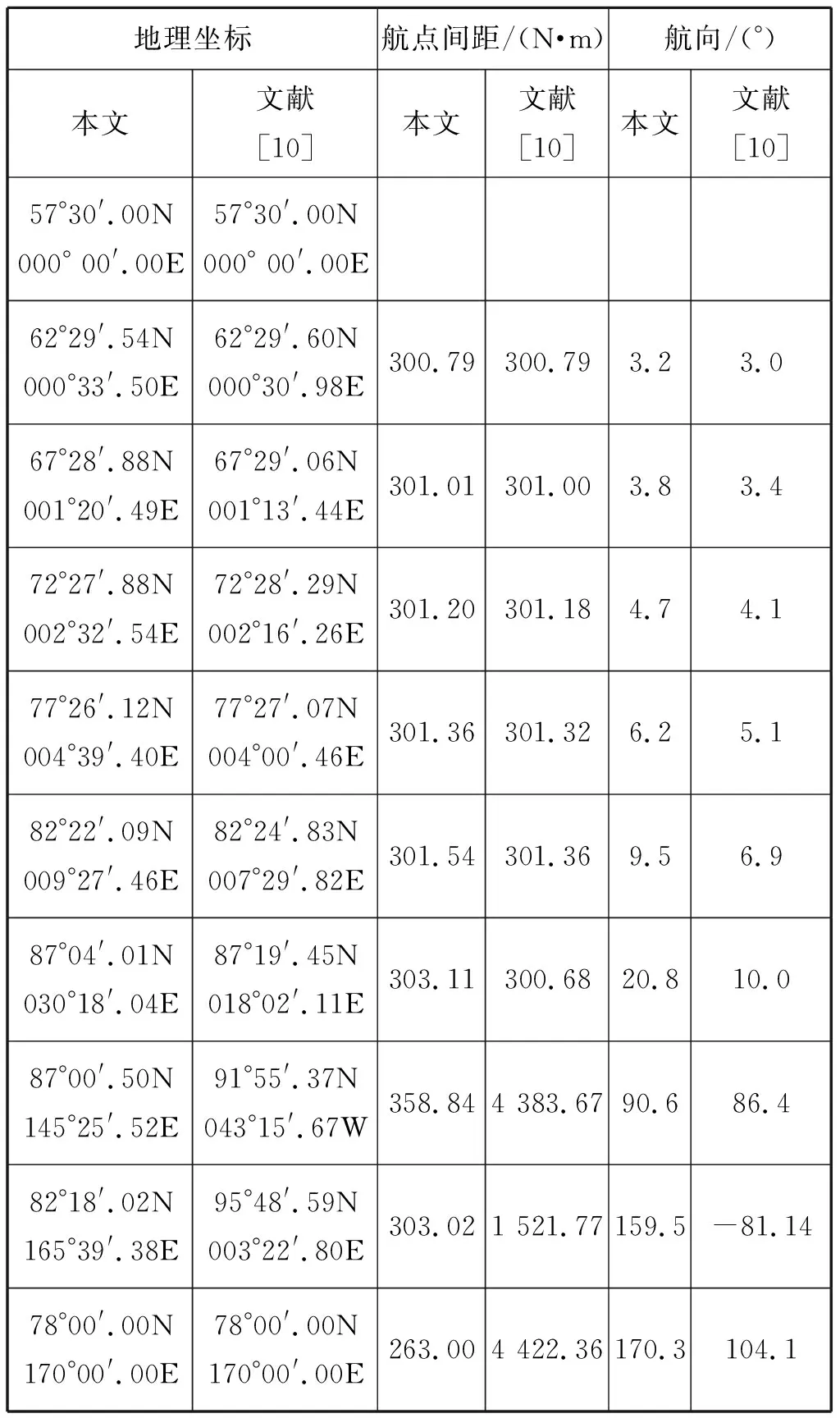
表5 采用本文方法所得航线设计结果

在该算例中，根据式(1)计算大圆距离为2 661.67 n mile，采用本文方法得到的设计结果超出72.2 n mile，主要原因在于第7个点与第8个点之间原本是按照300 n mile左右距离划分的，但因极区附近经度跨度较大，在采用恒向线计算时，距离偏差增大，进一步对该段作分段处理，增加中间点，会使总距离进一步减小。由于起始点到目标点的纬度是增大的，在采用文献[10]中的方法设计时，纬度变化量Δφ取正值，使得设计结果的纬度值持续增大，到第8个点时完全偏离大圆航线，从而导致设计结果不可信。

综上所述，本文方法可有效弥补文献[10]中的方法在航线设计中存在的不足，在极区附近、高纬度地区及航线起始点与目标点纬度接近等情况下都能实现等距离大圆航线的准确设计，设计过程中不存在航向奇异现象，且能适用于一般情况下的航线设计，充分证明了本文方法的优越性和广泛适用性。

3 结束语

大圆航线可采用等经差和等距离2种方法进行设计，本文从等距离设计理念出发，针对当前设计方法存在的不足，基于球面三角形特性推导等距离大圆航线的设计实现过程，通过对比分析说明了文献[10]近似方法的使用局限性和产生偏差的根源，验证了本文方法在高纬度地区、极区附近及航线起始点与目标点纬度接近等情况下的准确性和有效性，验证了设计过程中不存在航向奇异现象及对一般航线设计的适用性，充分说明了本文方法的优越性和广泛适用性，为该方法的推广应用奠定了基础。

[1] 程传林, 周利江. 利用MATLAB解析法求解大圆航线[J]. 中国水运, 2008,8(4):20-21.

[2] 仇健, 康卫民. 以计算中间点的方法绘制大圆航线及Excel辅助计算[C]//中国航海科技优秀论文集, 2010: 59-65.

[3] SKOPELITI A, TSOULOS L. Choosing a Suitable Projection for Navigation in the Arctic[J]. Marine Geodesy, 2013,36(2): 234-259.

[4] APGAR H. CAIV: A Process and Methodology[C]//AIAA Space Technology Conference & Exposition, 2011: 99-103.

[5] 揭军武. 三种大洋航线的分析与选择[J]. 中国水运, 2014,14(3):35-36.

[6] 李方能, 李厚朴, 吴延坤. 基于改进椭球模型的航线算法[J]. 舰船电子工程, 2014,34(7):81-85.

[7] 刘文超, 卞鸿巍, 王荣颖，等. 大椭圆航线设计的空间矢量方法[J]. 测绘学报, 2015,44(7):741-746.

[8] 郑亚波, 郭海亮, 李伟. 基于三维GIS平台的大圆航线三维可视化[J]. 指挥控制与仿真, 2015,37(6):128-132.

[9] 陈志平, 杜一村. 基于墨卡托海图的大圆航线设计[J]. 南通航运职业技术学院学报, 2016,15(2):25-28.

[10] 洪德本. 解析法大圆航线的设计[J]. 大连海事大学学报(自然科学版), 1997,23(4):22-24.