城市天然气短期日需求量预测新模型

舒 漫 刘夏兰 徐 婷 谢雯娟 何 斌

1.成都理工大学管理科学学院 2.中国石油西南油气田公司天然气经济研究所 3.中石油大英燃气有限责任公司

0 引言

天然气作为一种低碳高效清洁能源，正逐步成为中国能源结构转型的重要选择之一。近年来，中国天然气储量、产量和消费量均呈现出快速增长的趋势[1]。尽管天然气消费量增长显著，但天然气在我国一次能源消费结构中的占比仍仅为6.2%，远远低于世界平均水平。由此可以预见，未来我国天然气消费市场仍具有巨大的增长发展潜力[2]。城市天然气是天然气使用的重心，2016年中国城市天然气消费量在天然气消费总量中的占比达到32.5%。因此，如何完善城市天然气供需系统，确保城市天然气的利用达到最大化，不仅是每个城市天然气公司都需要考虑的问题，而且也是政府制定相关天然气政策的基础和前提[3]。除此之外，准确地预测短期城市天然气需求量，对于城市天然气的合理调峰调压、安全供应、管网优化等也有着重要的现实意义。

城市天然气短期需求量预测结果受到多种因素的共同影响，并且有关因素大多数都具有显著的随机不确定特点，使得城市天然气需求量预测演变为典型的非线性问题，简单的数学预测模型已经不能满足要求[4]。目前，城市天然气短期需求量预测模型主要包括时间序列[5]、回归分析[6]、支持向量机[7-8]、灰色关联[9]等，但其精度均不很理想。神经网络[10-11]的精度虽然较高，但其因遵循经验风险最小化的基本原则而容易导致过度学习，也容易陷入局部最小值，降低了泛化性。较之于上述诸多模型，最小二乘支持向量机基于结构风险最小化的原则，对于非线性问题也能得到较高的精度和泛化性，并且不容易出现过拟合现象[12]。因此，本文综合分析讨论了短期城市天然气日需求量的影响因素，结合这些影响因素，利用最小二乘支持向量机（LS-SVM）建立了城市天然气短期日需求量预测新模型；并且在仿真实验中，以四川省成都市为例，验证了新模型的实用性和有效性，以期为城市天然气短期日需求量的预测提供依据和参考。

1 城市天然气短期日需求量预测新模型

1.1 影响因素的选取

以往的研究所选取的短期城市天然气需求量影响因素大多局限在气温、季节、重大节假日、星期属性等[13-14]。笔者经过全面综合分析后，将影响因素确定为气象维、日期维以及政策维。以下分述之。

1.1.1 气象因素

气象包括温度、湿度、天气状况、降雨量、风级等，以往的短期城市天然气需求量预测多采用温度作为气象维唯一的影响因素[13-14]，很少考虑其他子因素。笔者通过各子因素与城市天然气用量的相关性大小排序发现，日最高温度、日平均湿度、空气质量指数（AQI）和PM2.5指数（大气中直径小于或等于2.5 μm的颗粒物含量）等4个气象子因素与城市天然气使用量的相关性位居前四位，全面考虑后选定这4个子因素作为气象维子因素。其中，选取日最高温度是因为城市天然气用户产生城市天然气使用需求时，一般都是在温度较高的时段[14]，并且日平均温度的计算尤为复杂。因此，选取日最高温度比日平均温度更为合理。

1.1.2 日期因素

城市天然气的使用量受日期变化的影响，从数据来看，城市天然气用量呈现冬春两季波动明显且用量明显增高的态势，而夏秋两季则呈现波动较为平稳并且用量较低的态势。此外，节假日和周末的天然气用量与平时相比也存在着一定的差别。因此，最后拟定季节、节假日以及星期属性作为3个日期子因素。

1.1.3 政策因素

城市天然气的使用与衣食住行息息相关，城市天然气需求量在一定程度上受与城市天然气相关行业的动荡影响，而行业动荡程度又受到政府政策的影响。因此笔者经全面考虑后，加入了政策维因素。政策包括价格政策和宏观调控政策，价格属于刚性指标，在短期内变化不大，因而本文选择的政策即宏观调控政策，将政策分为内部直接影响政策和外部环境影响政策，经过相关性分析分别选定天然气政策和房地产政策。

最终的影响因素指标体系如图1所示。

1.2 影响因素的处理

1.2.1 气象因素

气象因素的4个子因素中， PM2.5指数和空气质量指数属于定量数据，这2个指数都是逆指标，选择极差变换法作标准化，逆向指标为：

式中yi表示第i个标准化后数据值；xi表示第i个原始数据值；m表示需要标准化指标的总数。

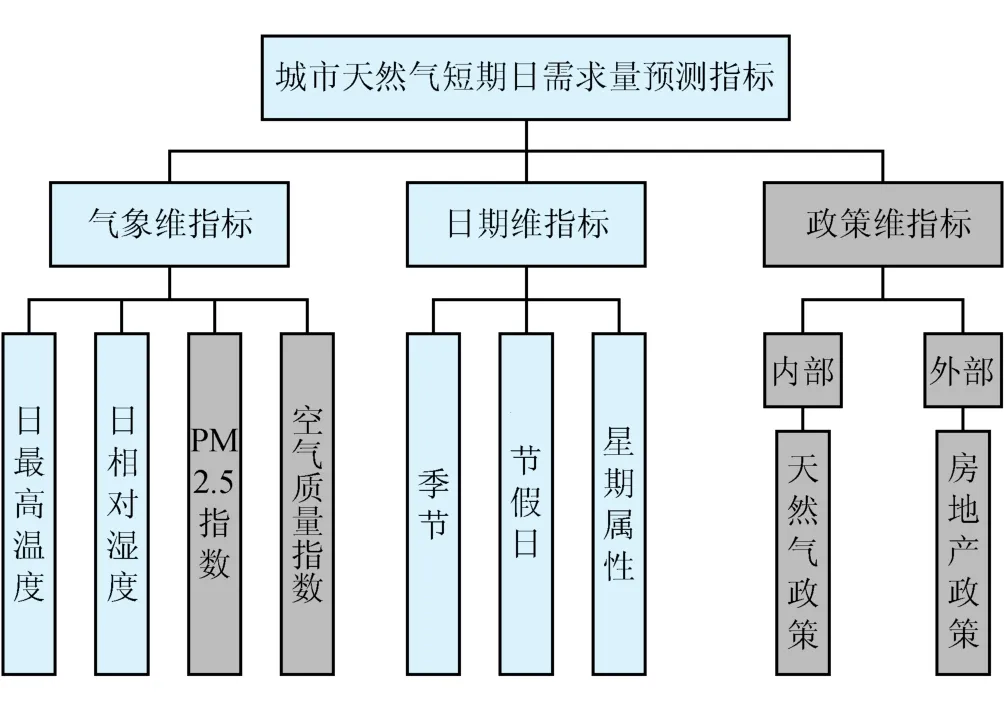
图1 指标体系图

日最高温度和日相对湿度不能根据原始数据来判断其好坏程度，不能明确地归类为属于正指标还是负指标，具有一定的模糊性，只能根据数值来确定对人体的舒适程度，再将这种定性的判断转换为定量数据。因此，笔者选用了模糊综合评判法来处理，根据本文参考文献[15]确定指标等级标准，如表1所示。模糊综合评价算法流程如图2所示。

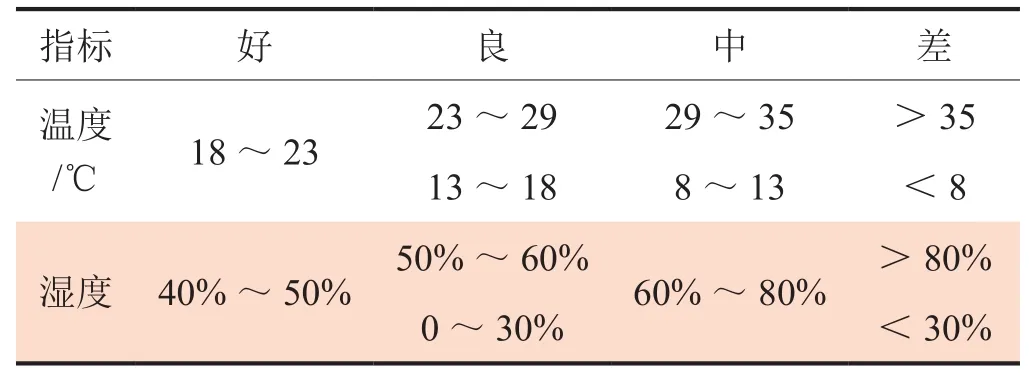
表1 温度、湿度指标等级划分表

图2 模糊综合评价算法流程图

1.2.2 日期因素

日期因素的3个子因素——季节、节假日以及星期属性都是定性数据，采用经验打分方式[16]来处理数据，其中在星期属性的处理中有别于以往将一周分为周一至周日[16]，而是将一周分为工作日和非工作日两类，经验打分表如表2所示。

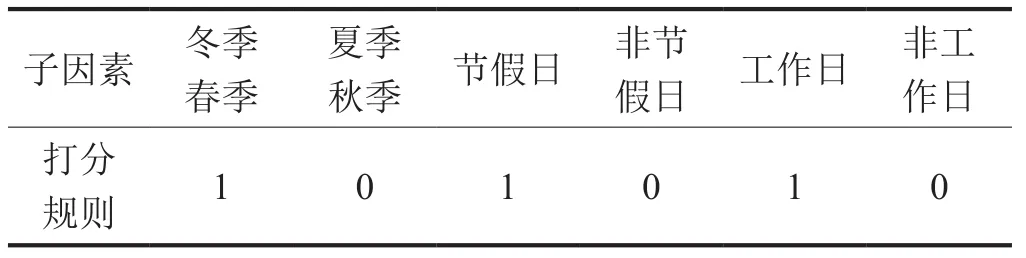
表2 季节、节假日、星期属性打分表

1.2.3 政策因素

政策因素中天然气政策和房地产政策都是定性数据，但房地产政策的实施效果可以用定量指标加以代替。因此，选取日住房成交量作为房地产政策的代替指标，日住房成交量是正向指标，采用极差变换进行处理（公式2）。考虑到政策的实施效果是人为感受的，天然气行业专家对于相关政策的感受是最为敏捷的。因此选择专家评分法对无法定量分析的天然气政策进行定性评估，选取10位业内专家对天然气政策进行评分，专家评分表如表3所示。此外，由于政策的实施进度无法度量，因而本文不考虑政策的滞后性。正向指标为：

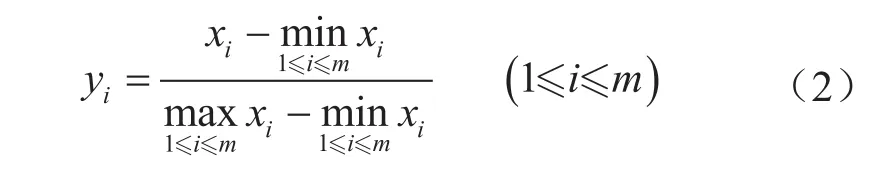
表3 业内专家对天然气政策的评分结果表

1.3 模型的建立

笔者利用最小二乘支持向量机（LS-SVM）基于气象、日期和政策三维影响因素建立了城市天然气短期日需求量预测新模型，核函数选取高斯核函数，采用十倍交叉验证的方法来调试核参数（σ）和惩罚因子（γ）。使用平均绝对百分比误差来评价该模型预测结果的准确度，平均绝对百分比误差（eMAPE）计算见公式（3）。整个模型的计算流程如图3所示。

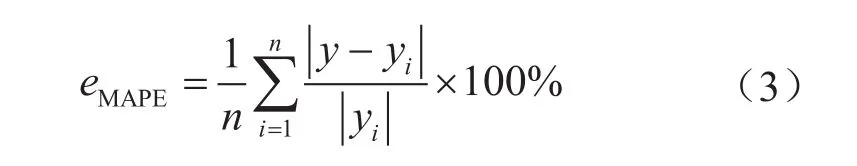
式中y和yi分别表示实际值和预测值。

2 仿真实验

笔者采用四川省成都市某城市天然气公司2016年5月1日—6月30日城市天然气用量数据作为训练数据，采用2016年7月1—15日数据作为测试数据，建立了成都市城市天然气短期日需求量预测新模型。经调试，最终确定模型惩罚因子γ＝1，核参数σ2＝5。新模型（LS-SVM）预测结果与ARIMA(1,1,13)、灰色关联、ВP神经网络、非线性回归等方法的预测结果对比如图4所示。从图4可以看出，新模型预测结果优于其他模型预测结果。新模型预测结果平均绝对百分比误差为1.423%，小于其他模型预测结果平均绝对百分比误差，模型精度优于其他模型。各种模型平均绝对百分比误差对比如表4所示。综上所述，本文所建立的城市天然气日需求量预测新模型预测效果好，精确度和可信度高，能够对上游供气公司合理调度、调峰调压和保障安全供应提供帮助，也可以为行业管理者和决策者做出科学决策提供依据和参考。

图3 算法流程图

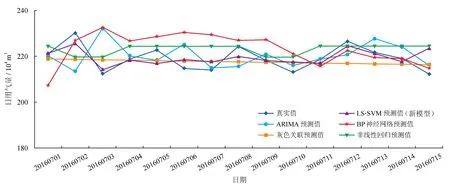
图4 多种模型预测结果对比图

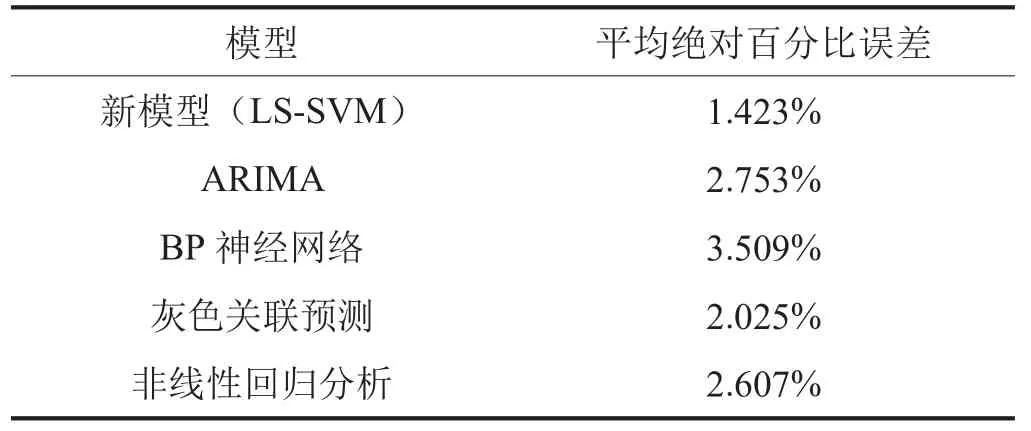
表4 多种模型平均绝对百分比误差对比表

3 结论与建议

笔者基于最小二乘支持向量机建立了高精度的城市天然气日需求量预测新模型，并以成都市为仿真实例验证了其合理性。该模型可以为天然气市场短期日需求量预测提供一定的帮助。基于本项研究的认识和成果，笔者得出了以下结论并提出相关建议。

1）城市天然气需求量的影响因素繁多，需要全面考虑，不能以偏概全只选取最大的影响因素。本文通过分析讨论，天然气短期日需求量受到日最高温度、日相对湿度、PM2.5指数、空气质量指数、季节、节假日、星期属性、天然气政策、房地产政策多种因素的共同影响。

2）影响短期城市天然气需求量的因素掺杂定性数据和定量数据，合理选择处理方法有利于提高城市天然气日需求量预测模型的精度。

3）城市天然气需求量的预测方法的选择很多，本文所建立的模型较优于传统的算法，并且具有一定的通用性，可作为其他地区建立类似的天然气需求量预测模型的参考。

4）在城市天然气的短期需求量预测中，城市天然气的使用与民生行业息息相关，不仅要考虑城市天然气行业本身的情况，而且更应当时刻关注相关行业的动态以及政策变动。这样才有利于行业管理者和决策者做出精准的判断和决策。

5）城市天然气的使用与城市的环境状况有着一定的联系，对城市天然气短期需求量的预测应当考虑到城市的环境状况，天然气行业的管理者和决策者应多与环境监测相关部分合作。这样才有利于天然气行业的可持续发展。

[ 1 ] 郭威, 潘继平, 娄钰. “十三五”全国油气资源勘查开采规划2016年度目标执行情况评估[J]. 天然气工业, 2017, 37(8):125-131.Guo Wei, Pan Jiping & Lou Yu. Evaluation on the implementation of 2016 National 13thFive-Year oil & gas resources exploration and production planning[J]. Natural Gas Industry, 2017,37(8): 125-131.

[ 2 ] 康建国. 全球天然气市场变化与中国天然气发展策略思考[J].天然气工业, 2012, 32(2): 5-10.Kang Jianguo. Changes in global natural gas market and development strategy of natural gas in China[J]. Natural Gas Industry,2012, 32(2): 5-10.

[ 3 ] 汪丽娟. 基于粒子群优化的最小二乘支持向量机天然气负荷预测方法研究[D]. 上海: 华东理工大学, 2013.Wang Lijuan. Research on forecasting methods of natural gas based on partical swarm optimization—least squares support vector machine[D]. Shanghai: East China University of Science and Technology, 2013.

[ 4 ] 朱刚. 城市天然气管网负荷预测的研究[D]. 天津: 天津大学,2009.Zhu Gang. Study on city gas pipeline network load forecasting[D]. Tianjin: Tianjin University, 2009.

[ 5 ] 黄岳嵘, 徐晓钟, 张益铭, 王劲松. 基于ARIMA和神经网络模型的城市燃气负荷预测[J]. 计算机应用与软件, 2011,28(12): 206-209.Huang Yuerong, Xu Xiaozhong, Zhang Yiming & Wang Jinsong.Arima and neural network model based city gas load forecasting[J]. Computer Applications and Software, 2011, 28(12): 206-209.

[ 6 ] 叶倩, 陈晓慧, 谢扬. 基于通径分析的重庆市天然气消费量影响因素分析及预测[J]. 机械, 2010, 37(9): 1-4.Ye Qian, Chen Xiaohui & Xie Yang. The natural gas factors analysis and forecasting in Chongqing based on path coeきcient analysis[J]. Machinery, 2010, 37(9): 1-4.

[ 7 ] 张超, 刘奕, 张辉, 黄弘. 基于支持向量机的城市燃气日负荷预测方法研究[J]. 清华大学学报(自然科学版), 2014, 58(3):320-325.Zhang Chao, Liu Yi, Zhang Hui & Huang Hong. Study on urban short-term gas load forecasting based on support vector machine model[J]. Journal of Tsinghua University (Natural Science Edition), 2014, 58(3): 320-325.

[ 8 ] Вai Y & Li C. Daily natural gas consumption forecasting based on a structure-calibrated support vector regression approach[J].Energy & Вuildings, 2016, 127: 571-579.

[ 9 ] Zeng В & Li C. Forecasting the natural gas demand in China using a self-adapting intelligent grey model[J]. Energy, 2016, 112:810-825.

[10] Demirel OF, Zaim S, Caliskan A & Ozuyar P. Forecasting natural gas consumption in Istanbul using neural networks and multivariate time series methods[J]. Turkish Journal of Electrical Engineering & Computer Sciences, 2012, 20(5): 695-711.

[11] Kizilaslan R & Karlk В. Comparison neural networks models for short term forecasting of natural gas consumption in Istanbul[C]//International Conference on Applications of Digital Information& Web Technologies, 2008, Ostrava, Czech Republic. New York:IEEE, 2008.

[12] 康传会. 基于最小二乘支持向量机的磁滞建模[D]. 金华: 浙江师范大学, 2010.Kang Chuanhui. Hysteresis modeling based on least squares support vector machines[D]. Jinhua: Zhejiang Normal University,2010.

[13] 李谦益, 吴渊. 基于气温累积效应的冬季天然气日负荷预测——以西安市为例[J]. 油气储运, 2016, 35(9): 1014-1017.Li Qianyi & Wu Yuan. Forecast on daily gas load based on the accumulative effect of temperature in winter: A case study of Xi'an[J]. Oil & Gas Storage and Transportation, 2016, 35(9):1014-1017.

[14] 何春蕾, 段言志, 邬宗婧, 杨光道. 基于气温的城市燃气短期日负荷预测模型——以四川省成都地区为例[J]. 天然气工业,2013, 33(4): 131-134.He Chunlei, Duan Yanzhi, Wu Zongjing & Yang Guangdao . A short-term forecasting model of city gas daily load based on air temperature[J]. Natural Gas Industry, 2013, 33(4): 131-134.

[15] Qiu Zeyang, Liang Wei, Wang Xue, Lin Yang & Zhang Meng.Study on quantitative risk assessment model of the third party damage for natural gas pipelines base Lin d on fuzzy comprehensive assessment[J]. Journal of Physics: Conference Series, 2017,842: Conference 1.

[16] 刘涵, 刘丁, 郑岗, 梁炎明, 宋念龙. 基于最小二乘支持向量机的天然气负荷预测[J]. 化工学报, 2004, 55(5): 828-832.Liu Han, Liu Ding, Zheng Gang, Liang Yanming & Song Nianlong. Natural gas load forecasting based on least squares support vector machine[J]. CIESC Journal, 2004, 55(5): 828-832.