光学显微镜自动聚焦算法研究

吕美妮， 玉振明

(1. 桂林电子科技大学信息与通信学院，广西 桂林 541004;2. 梧州学院 广西高校图像处理与智能信息系统重点实验室，广西 梧州 543002)

0 引 言

自动聚焦技术是光学显微镜成像系统中至关重要的技术，决定其准确度、效率和稳定性。自动聚焦技术主要分为主动式和被动式[1]。主动式聚焦技术主要通过测量被测物体与成像面的距离，再利用成像原理计算出离焦量。被动式聚焦技术是基于数字图像处理，通过对采集到的图像进行数据分析，判断当前图像的聚焦程度。由于被动式聚焦技术不需要添加额外的传感器，仅利用获取的图像序列就能进行分析系统的聚焦状态，因此近年来得到广泛应用[2]。被动式自动聚焦技术主要分为两类：一类是聚焦深度法（depth from focus，DFF）；另一类是离焦深度法（depth from defocus，DFD）[3]。DFD需要建立一定的数学模型，通过分析离焦图像信息，确定模糊程度和离焦图像的关系，估算出当前位置与聚焦位置的距离。但由于各成像系统的结构不同，建立数学模型所需的参数存在一定的差异，故DFD在实际应用中并不广泛。而DFF无需建立复杂的数学模型，只需要通过分析图像的分布特点来灵活选取聚焦窗口以及评价函数，适用性较高。其中，聚焦深度法主要包括3个核心问题：聚焦窗口的选择，聚焦评价函数的选取和搜索算法的布置[4]。

本文主要研究聚焦窗口的选择以及聚焦评价函数的选取。在聚焦窗口选择算法方面，针对传统的聚焦窗口选择方法不能灵活选取聚焦区域的问题，提出一种根据图像子块梯度幅值总和变化量的聚焦窗口选择方法。而在选取聚焦评价函数方面，针对传统的聚焦函数受噪声影响而引起曲线失去理想特性的问题，提出一种基于梯度和方差的改进算法。

1 聚焦窗口

聚焦窗口的选取直接影响着后续聚焦算法的计算量、复杂度和准确度[5]。传统的聚焦窗口选择方法有中央选择法[6-7]、倒T型选择法[8]和黄金多点选择法[9]等。这些方法一般先假设被测目标的位置是固定的，或其分布有一定的规律性，一旦被测目标偏离或是遇到稀疏内容图像时，传统的方法具有一定局限性。所以寻求更灵活的聚焦窗口选择方法成为研究的热点。

1.1 理论知识

图像均值可以作为图像分割的阈值，以此大致区分背景区域和目标区域。基于此原理，对显微图像序列进行分块，主要分为零内容子块（包括边缘含有部分内容区域，可忽略不计）、稀疏内容子块（内容区域占子块内容的比小于等于1/2）和丰富内容子块（内容区域占子块内容的比大于1/2）3种。通过分析，不难看出零内容子块的每个像素灰度值几乎都大于图像均值，丰富内容子块的每个像素灰度值几乎小于图像均值，而稀疏内容子块中，如果是包含较少内容区域，子块中像素灰度值大于图像均值的像素个数占多数；反之，如果包含较多内容区域，子块中像素灰度值小于图像均值的像素个数占多数。

为了验证子块均值与图像均值之间的关系，本文利用光学显微镜XSZ-8100采集内容丰富程度不同的图像序列（离焦-聚焦-离焦），进行分析整理，数据取其平均值。对图像内容稀疏的图像序列，因其含有内容区域的子块较少，故内容子块中含内容区域较少的子块，统一归为零内容子块（不考虑玻片杂质的影响）。

从表1可以看出，对于图像内容丰富和相对丰富的图像序列，丰富内容子块的均值一般分布在[E-20,E-10]内，在此范围内也含有一部分的其他两类子块，但丰富内容子块数量占图像子块总数的比例较大，而在小于E-20的范围内，虽然在此范围内也含有一部分的其他两类子块，但含大部分内容子块的数量占了很大的比例，并且子块数量占图像子块总数的比例较小，故阈值选取在E-20能初步判定聚焦窗口的大致区域，剔除大量的无用图像子块。在图像内容较稀疏的情况下，因丰富内容子块较少，阈值选取在任何范围内，零内容子块所占的比例较大，故后续介绍的方法适用于除稀疏内容图像（目标区域零星分布）之外的任意显微图像序列。

表1 图像子块均值分布范围表1）%

1.2 聚焦窗口选择算法

本文的聚焦窗口选择算法先通过表1设定阈值剔除大量的无用子块，再根据子块的梯度幅值总和的变化量确定聚焦窗口。具体步骤如下：

1）对像素大小为M×N的图像f求图像均值：

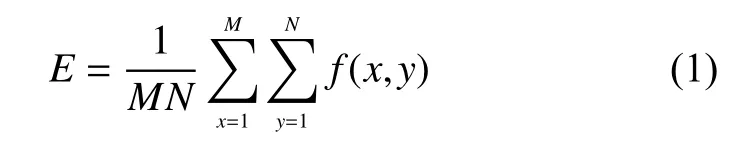
其中f(x,y)为图像像素点(x,y)处的灰度值。

2）把图像分割为w×w大小的m×n个子块，根据式（1）求图像子块均值：

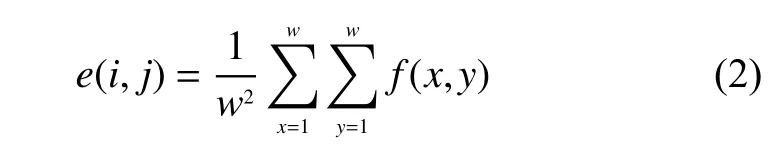
其中为图像子块坐标。

3）根据子块均值大小对子块进行二值化处理：

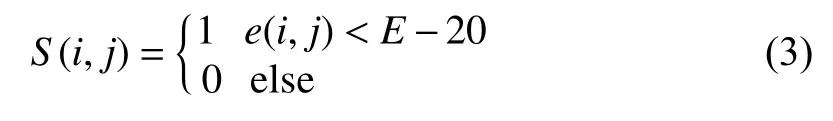
同时根据子块二值化结果对图像块进行筛选，保留S(i,j)>0的子块，剔除大量无用的子块S(i,j)<0。

4）定义图像在点(x,y)处的梯度为

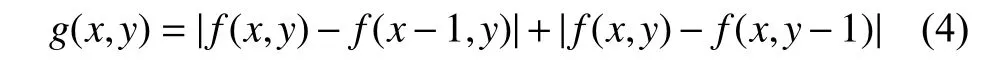
因此子块(i,j)的梯度幅值变化总和为

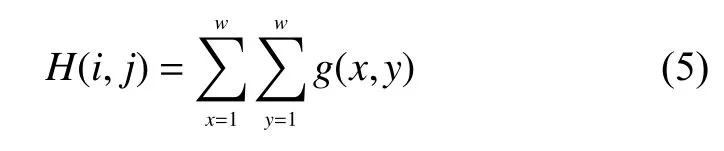
因此沿Z轴移动子块(i,j)梯度幅值总和差值为

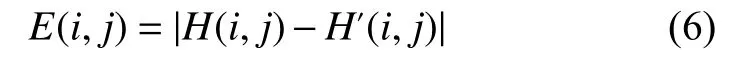
其中H′(i,j)为显微镜载物台沿Z轴移动一小段距离后同一位置子块的梯度幅值总和。

判断图像子块是否满足式（4）～式（6），若满足要求，则从满足条件的图像子块中选取E(i,j)变化最大的两个图像子块作为聚焦窗口。

在聚焦过程中，只有内容像素的梯度幅值发生显著变化，而杂质像素和背景像素的梯度幅值基本不变[10]。内容子块的E(i,j)变化较为明显，零内容子块的E(i,j)基本不变（或在一定的范围内波动），故选取E(i,j)变化最大的两个子块作为最终的聚焦窗口。

2 聚焦评价函数

传统的聚焦函数分为3类：梯度类评价函数、频域类评价函数和统计类评价函数[11-12]。其中基于频域的聚焦评价函数比较复杂，计算量大，在实际应用中并不多。而基于梯度类函数与统计类函数因计算简单，在实际应用较为广泛。

传统的聚焦评价函数易受噪声的影响，引起函数性能下降，进而导致聚焦的不准确。本文提出一种基于梯度和方差的改进算法，该算法将梯度评价函数与方差评价函数结合，利用每个像素的权重进行加权，计算简单且能提高其灵敏度、清晰度比率和抗噪性。

在传统的聚焦评价函数中，Tenengrad函数是性能比较优异的梯度类函数。该函数基于Sobel算子，由于Sobel算子结合了高斯平滑和微分，所以Tenengrad函数对噪声具有很强的稳健性。故本文选用性能较好的Tenengrad函数来构建新的聚焦评价函数。

对图像f每个像素点(x,y)的水平及垂直差分进行平方运算，在一定程度上可起到抗噪声的作用。

其中gx(x,y)和gy(x,y)分别表示图像与水平和垂直Sobel算子的卷积。

由于清晰图像一般比离焦图像具有更大的梯度变化，因此图像的梯度值方差同样也可以区分内容像素和背景像素。故对每个像素点的p(x,y)进行求方差，方差反映数据波动的大小，可看出每个像素点p(x,y)的偏离程度。

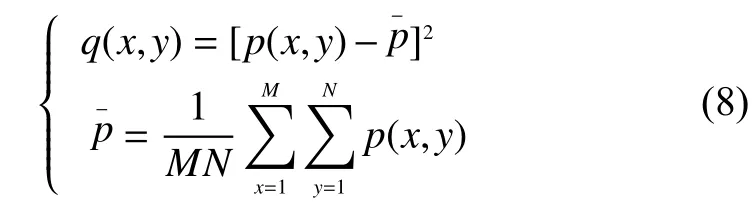
其中是图像每个像素点p(x,y)的平均值。

不同的像素有不同的作用，而在聚焦过程中，背景像素和杂质像素会影响聚焦函数的曲线性能，为了减少其影响，对q(x,y)用像素的灰度值权重进行加权。

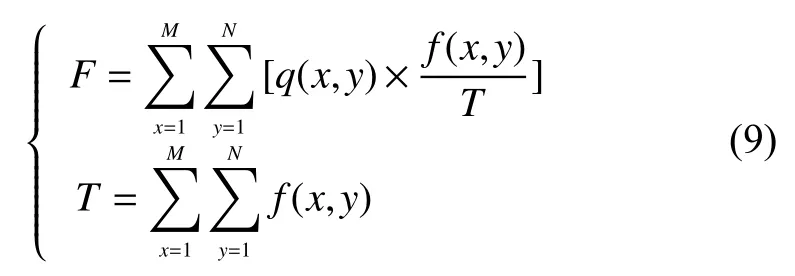
其中T为图像的灰度平均值，F为聚焦评价函数值。在聚焦过程中，背景像素和杂质像素的灰度值基本不变（或变化很小），而内容像素的灰度值发生显著的变化。利用这个性质，可以发现在聚焦过程中，内容像素的灰度值权重越来越大。通过对q(x,y)进行加权，使得内容像素的q(x,y)比重加大，而背景像素和杂质像素的q(x,y)比重减少，进一步突出了聚焦图像和离焦图像的区别，在一定程度上提高了聚焦函数的灵敏度。

3 实验与分析

本文实验坏境为：CPU，Intel（R）Core（TM）i7-6700 3.4GHz；RAM，8.00GB；Matlab（R2014a）。

本文实验图片（480×640）均通过梧州奥卡光学仪器公司研发的光学显微镜（XSZ-8100）进行采集。实验中选用2组图像大小为480×640的显微图像序列（离焦-聚焦-离焦），聚焦图像如图1（a）～图1（b）所示。图中所示的图像序列，最佳聚焦位置在第41帧。

图1 显微图像序列

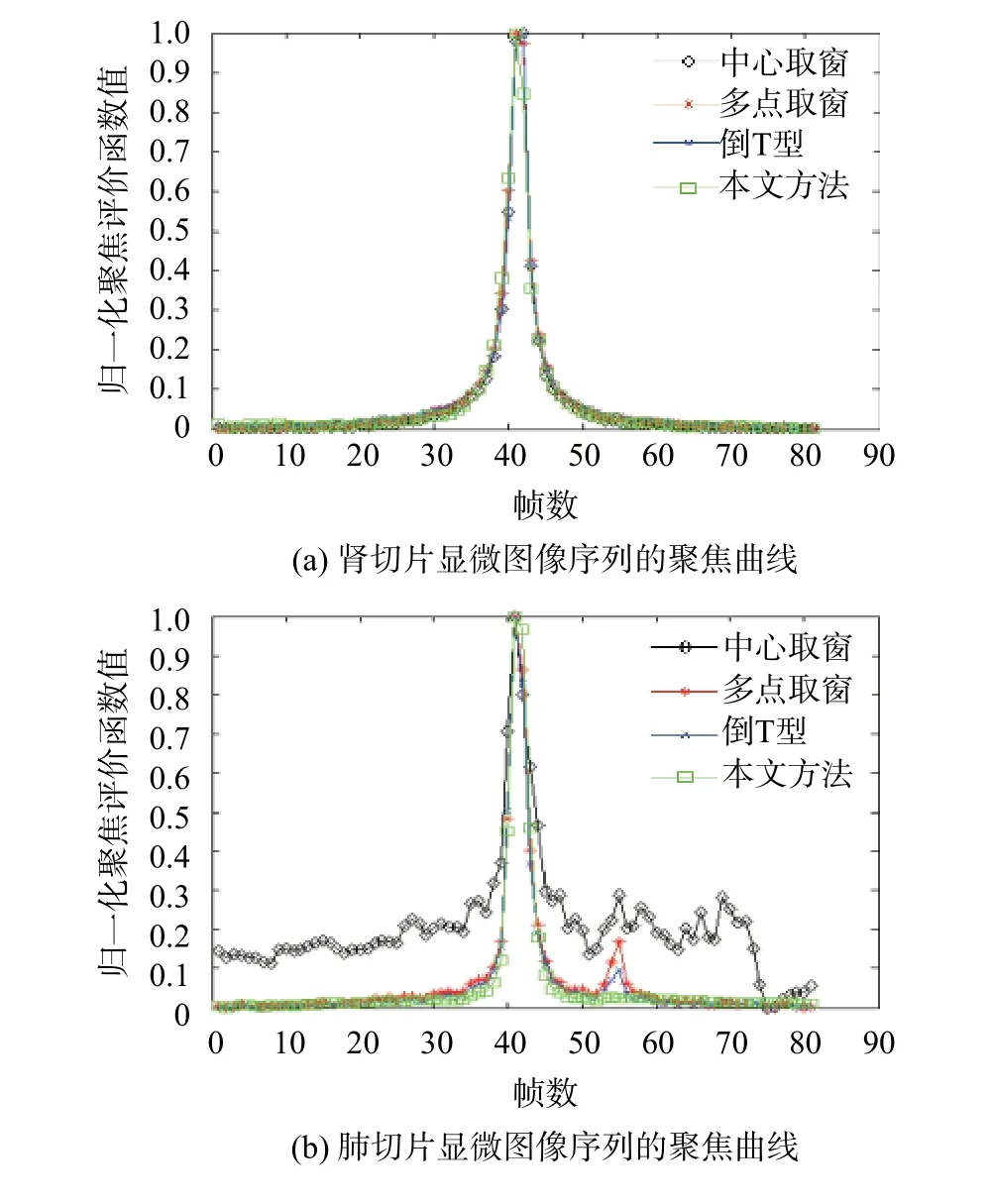
图2 取窗方法对比曲线图

3.1 聚焦窗口选择实验

为了验证本文方法的有效性，分别与中心选择法、多点选择法和倒T选择法进行对比实验，聚焦评价函数采用性能优异的Tenengrad函数。实验仿真结果如图2所示。

从实验结果来看，对于内容丰富的图像序列(图1（a）），传统的方法和本文方法都能够使聚焦评价函数曲线具有单峰性，不存在局部峰值。这是由于图像内容丰富，传统的取窗方法也能纳入更多的图像内容。而当被测物体偏离中心区域（图1（b）），在取窗足够大的情况下，传统的取窗方法能纳入一部分的图像内容，但由于纳入的非内容区域过多，会导致曲线出现局部极值，而本文方法的曲线还能保持曲线的单峰性。可见本文方法能确保选取到含有大量内容区域的子块作为聚焦窗口。

3.2 聚焦函数性能实验

3.2.1 仿真实验

为验证本文函数的性能，选取Variance函数[13]、Robert函数[14]、EOG函数[15]、Tenengrad函数[15]以及文献[16]的SV函数（Sobel函数和方差函数结合）进行对比实验。聚焦窗口的选取方法则选用本文1.2所提的方法。图3（a）是无噪声情况下的仿真曲线。图3（b）则是图像序列加入随机噪声的仿真曲线。

图3 聚焦函数仿真曲线图

由图可知，当无噪声干扰时，传统的聚焦评价函数和本文函数均满足单峰性和无偏性，且保持理想曲线的特性，但本文函数灵敏度更高。当有噪声干扰时，本文函数的仿真曲线还能保持单峰性和无偏性，且平缓区波动较小，而其他评价函数的仿真曲线波动较明显，失去理想曲线的特性，说明本文函数具有较好的稳定性。

3.2.2 结果分析

为了验证本文算法性能上的改进，利用文献[15]中提出的评价指标对各聚焦函数进行定量分析。

清晰度比率表达式为

其中Fmax和Fmin为聚焦函数的最大值和最小值（最小值应在聚焦曲线的平缓区取得）。

灵敏度因子表达式为

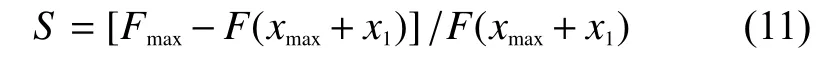
其中x1为横坐标变化量，xmax为函数最大值的横坐标。

首先假设采样点有N个（曲线的平缓区取得），则定义N个点的函数值标准差为平缓区波动量，其表达式为

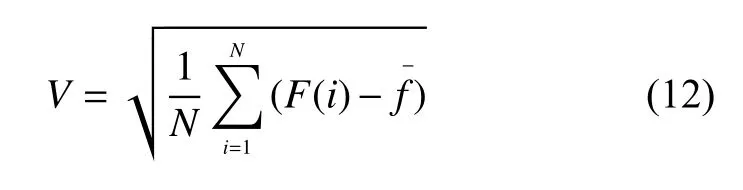
其中为平缓区的灰度均值。

对各函数进行定量分析如表2所示，给出在随机噪声的影响下，各函数的清晰度比率（R）、灵敏度因子（S）、平缓区波动量（V）和处理时间（T）。

表2 图像在噪声干扰下各聚焦函数性能指标

从表2可以看出，本文函数的灵敏度明显高于其他函数，说明本文函数在有噪声的影响下，函数最大值附近变化剧烈，适用于细聚焦过程。本文函数的清晰度比率明显高于其他函数，说明本文函数在有噪声的情况下，对不同离焦程度的图像分辨能力强，这也说明该函数抗噪声能力较强。本文函数的平缓区波动量小，说明该函数在噪声的干扰下还能保持平缓区波动平衡，稳定性较强。从时间来看，本文函数相比于传统聚焦评价函数，时间相差不大。本文提出的算法是基于文献[16]的基础上进行改进的，相比于文献[16]的SV算法，本文算法的清晰度比率、灵敏度因子和平缓区波动量都有了提高，并且实验用时比SV函数少。

从以上分析的结果来看，本文提出的算法在抗噪性、灵敏度和稳定性方面具有一定的优势，且适用于光学显微成像系统。

4 结束语

在光学显微镜系统聚焦的过程中，传统的聚焦窗口选择方法并不能满足聚焦的要求，一旦目标区域偏离中心区域或是目标区域较小，往往都会导致聚焦失败。本文提出的新算法能选取到含内容区域较多的图像块作为聚焦窗口。聚焦评价函数是自动聚焦的核心问题之一，一个理想的聚焦函数，应该满足无偏性、单峰性和抗噪性。本文提出的算法在噪声的干扰下，具有较高的灵敏度、稳定性和抗噪性。综上，本文提出的聚焦窗口选取方法以及聚焦评价函数适用于显微成像系统中。

[1]蒋涛, 左昉, 王灵国. 严重离焦状态下的自动聚焦实现[J]. 激光技术, 2015, 39(6):794–797.

[2]李惠光, 王帅, 沙晓鹏,等. 显微视觉系统中自动聚焦技术的研究[J]. 光电工程, 2014, 41(8):1–9.

[3]彭国晋. 远程显微工作站视频信息处理研究及应用技术开发[D]. 桂林: 桂林电子科技大学, 2015.

[4]商艳芝, 江旻珊. 光显微成像系统自动对焦技术的研究[J].光学仪器, 2016, 38(2):145–148.

[5]尤玉虎, 刘通, 刘佳文. 基于图像处理的自动对焦技术综述[J].激光与红外, 2013, 43(2):132–136.

[6]陈国金. 数字图像自动聚焦技术研究及系统实现[D]. 西安:西安电子科技大学, 2007.

[7]HE J, ZHOU R, HONG Z. Modified fast climbing search auto–focus algorithm with adaptive step size searching technique for digital camera[J]. Consumer Electronics IEEE Transactions on, 2003, 49(2):257–262.

[8]朱孔凤, 姜威, 高赞,等. 自动聚焦系统中聚焦窗口的选择及参量的确定[J]. 光学学报, 2006, 26(6):836–840.

[9]李奇, 冯华君, 徐之海. 自动对焦系统中图像非均匀采样的实验研究[J]. 光子学报, 2003, 32(12):1499–1501.

[10]翟永平, 刘云辉, 周东翔,等. 稀疏图像内容情况下显微镜自动聚焦算法[J]. 软件学报, 2012, 23(5):1281–1294.

[11]朱倩, 姜威, 贲晛烨,等. 梯度与相关性结合的自动聚焦算法[J].光学技术, 2016, 42(4):329–332.

[12]莫春红, 刘波, 丁璐,等. 一种梯度阈值自动调焦算法[J]. 红外与激光工程, 2014, 43(1):323–327.

[13]CHEN G J, ZGU M J, WANG Y K, et al. Study on definition evaluation function based on image contrast variation[C]//Proceedings of the 2007 annual Conference on International Conference on Computer Engineering and Applications, 2007.

[14]高赞, 姜威, 朱孔凤,等. 基于Roberts梯度的自动聚焦算法[J].红外与激光工程, 2006, 35(1):117–121.

[15]翟永平, 周东翔, 刘云辉,等. 聚焦函数性能评价指标设计及最优函数选取[J]. 光学学报, 2011, 31(4):242–252.

[16]MO C H, LIU B. Research and realization of an anti–noise auto–focusing algorithm[C]//Proceedings of the 2012 Second International Conference on Electric Information and Control Engineering, 2012.