一个新格赖斯主义的语用推理模型及其形式刻画

郑植

北京大学 哲学系

legend05jbb@sina.com

1 导言

格赖斯提出的合作原则（[3]）一经问世就在语用学领域产生了巨大反响。格赖斯认为，人类在话语交际的过程中倾向于普遍遵守某种共同的准则，使得交际得以在不同个体之间顺利开展，格赖斯将其命名为“合作原则”。在这些原则的制约下，为了传达某些信息，说话者可以只说少量的、字面信息量弱于需传达的信息量的话，而让听话者自行推理出其余信息。这种推理现象称为会话隐涵。合作原则具体包含以下内容：

1.量（Quantity）准则：

a.话语应包含实现话语交际目的所必需的信息；

b.话语的信息量不应超出所需。

2.质（Quality）准则：

a.不说（自知是）虚假的话；

b.不说没有根据的话。

3.关系（Relation）准则：说话的内容要有相关性。

4.方式（Manner）准则：使用清楚明白的说话方式，具体包括避免晦涩、避免歧义、避免啰嗦、要有条理等要求。

格赖斯的合作原则提出了在语用领域人们的话语行为遵循的某种普遍性的规则和倾向，这些规则和倾向深藏于人的语言行为模式之中，决定着人的表层语用行为。这就与形式主义语言学“深层结构”和“普遍语法”的思路不谋而合，使得形式主义的语言学研究方法可以对曾经的“禁区”——语用学领域进行涉足。从而开辟了有形式主义倾向的语用学研究潮流。因此，合作原则的提出在一定程度上弥补了用形式方法分析自然语言意义时的不足，使得逻辑分析的方法可以应用于语用现象的研究。在此之前，数学和逻辑的方法仅限于研究“语形-语义”的问题，如一阶语义和蒙太古语法等，在语用领域缺乏理论基础并面临诸多困难。但合作原则的提出使得这一做法成为可能，如Horn级差理论（[4]），语境转化理论（[2]）等理论都在将数学方法应用于用学领域取得了一定的成功。但合作原则本身仍面临一些问题。格赖斯本人并未对合作原则之下的会话过程给出具体的数学模型和形式刻画。合作原则本身的普遍性与解释的适用性也面临不同程度的质疑。对于合作原则面临的不足，语言学家大致有三种不同态度：其一，取消话语交际的普遍原则。Keenan（[7]）认为普遍原则很难解释不同语言、不同文化背景主体间的交际行为。而Katz（[6]）直接将隐涵归约为语义问题。其二，认为话语交际的普遍原则是存在的，但应用其他更合理的原则来阐述，如Sperber和Wilson（[10]）主张用关联原则来代替合作原则。其三，在合作原则的基础上进行理论的发展和完善，称为新格赖斯主义。如Leech（[8]）认为应该用礼貌原则作为合作原则的补充；Horn（[5]）将合作原则重新阐释为Q原则（信息充分原则）和R原则（信息必要原则），并用“语用劳动分工”来解释简短话语同冗长话语在传递信息上的“分工合作”；而Levinson（[1]）提出了Q原则（量原则）、I原则（信息原则）和M原则（方式原则），每种原则都对说话人的说话方式和听话人的推理方式做出一定要求，会话双方在这些要求之下说话和推理。周礼全（[14]）在合作原则的基础上增加了态度准则来处理祈使句与疑问句。

本文将沿袭第三种立场，并借Sperber和Wilson的关联理论（[9,10]）对话语交际行为的”明示-推理”模式的见解，通过构建一个会话的推理框架，描写和刻画合作原则下会话参与者在该框架中的话语行为和推理过程，从而展现出格赖斯及其后继者提出的语用推理原则的一般功能和特性。

因此，本文试图采纳“话语承载信息”的视角，以此构造一个基于信息的会话推理模型。从这一的视角看，句子（陈述句）的意义应该是该句包含的“内容”或“信息”，即将句子解释为一组信息的集合，而不是像Gazdar和以往的许多语义学理论将句子的语义值处理成可能世界的集合。这种做法避免了后者在处理隐涵和预设问题时面临的某些难题，更加符合合作原则关注信息在不同主体间传达的初衷。因此本文提出的模型将不使用可能世界或“可能世界到外延的函数”来为句子提供语义解释机制，而是站在语言传达信息的角度上，采用“信息集”的观点来处理句子的语义值，并重点关注如何从一个话语事件（如某人说了某句话）来推知说话者知道的信息，即站在研究者的角度展示如何从说话者“说了什么”推知他“知道什么”的语用推理过程。

而在基于信息的会话推理模型的基础上，这样做也能对Horn，Levinson等人对合作原则提出的精细解释方案给出描写和刻画，展现这些方案形式上的共同点，一定程度上揭示出新格赖斯主义若干原则的逻辑实质。

最后，本文试图根据以上模型对于信息陈述类型的语用推理进行形式刻画。这包括给出一个形式系统，证明其可靠性。这表明形式化方法在语用领域中具有一定程度的可操作性与可应用性。

此外，需要指出的是，虽然格赖斯本人提出会话原则正是基于对将形式方法广泛用于自然语言时会出现偏差和局限的担忧：

毫无疑问，形式化方法尤其是经得起逻辑学家的系统化的对待和检验的，然而，仍有许多用自然语言而非按照形式化方法表述的推理和论证可被清晰辨别为有效。所以，一定还有这样一种逻辑的一席之地——它是未经简化的，因而也或多或少是非系统性的；但它能更自然地与这些形式化方法要表达的东西相对应。形式方法的简化的逻辑可以辅助或引导它，但不能取代它。实际上，这两种逻辑不仅不同，而且有时互相冲突。形式化方法中成立的规则对于这种“自然的对应”却未必适用。（[3]，第43页）

但是，如果会话原则正如格赖斯希望的那样扮演了一种“未经简化的、自然的逻辑”的角色，那么运用形式手段对这样一种逻辑的功能和特性进行分析和刻画，揭示其形式规律，发现它与“简化的逻辑”的冲突之处（如果真的存在的话）并力图弥合这种差距，显然也是有意义的。

2 新格赖斯主义对合作原则的发展

格赖斯提出的合作原则描述了语用活动中的某些一般倾向，但对其中的关键概念与原则并未给出严格的定义与形式刻画，仍有许多没有澄清的问题。例如，格赖斯一方面认为人们在交际时普遍遵守合作原则，但又承认人们常常通过不遵守合作原则来实现自己的会话意图（如特殊会话隐涵），这就使所谓“原则”的地位受到质疑；同时合作原则在面临跨文化语言现象时，其自身的普遍性也受到一定挑战。

新格赖斯主义者为了弥补这一缺陷而进行了若干尝试，如Horn（[5]）将合作原则重新阐释为Q原则（信息充分原则）和R原则（信息必要原则），并用“语用劳动分工”来解释简单语句和复杂语句在传递信息上的“分工合作”。

其中Q原则是基于听话者视角的，从说话者传达信息的意图来讲，说话者尽可能多说，提供详细而充分的信息，诱发上限会话隐涵；R原则是基于说话者视角的，同听话者接受和处理信息的难度来讲，要求说话者尽可能少说，只提供必要的信息，诱发下限会话隐涵。

举例来说，级差隐涵（[4]）是基于Q原则的上限会话隐涵。如果同一语义场的一组强度不同的表达式构成级差序列，如英语中的量词〈all,almost all,most,some,few〉（〈全部,几乎全部,大多数,一些,少数〉），那么说话者使用其中的某一项，如Some of the students attended the meeting（学生中一些人出席了会议），就意味着说话者知道自己不能使用更强的项，如不能使用All of the students attended the meeting（学生中所有人都出席了会议），即说话者总是提供最强的信息（参见量准则）。

假如说话者明知所有的学生都出席了会议，却还使用“Some of the students attended the meeting”，就明显是带有误导性的不合作的话语行为。

而R原则则从另一个方向发挥作用，即听话者听到了φ，但会认为说话者想表达的信息不只是φ本身的信息。典型的例子是所谓“间接话语行为”，如：Can you open the window?（你能把窗户打开吗？）该句形式上是一个“一般疑问句”，原则上应用“yes”或“no”来回答。但在一般的场合中，听话者会认为说话者问此问题并非只是想得知自己是否具有打开窗户的能力，而是要求比字面信息更多的东西——让自己做出将窗户打开的实际行动。因此R原则允许说话者“说出的少于想说的”，并使听话者“知道的多于听到的”。

Horn的Q原则和R原则展现了两种相反的说话方式，或语言的编码原则，揭示了会话过程中说话者和听话者就话语编码问题上潜在的矛盾，以及双方如何相互合作以解决这一矛盾，从而实现交际目的的过程。这是对合作原则的有益补充和推进。

Levinson（[1]）则提出了Q原则（量原则）、I原则（信息原则）和M原则（方式原则）来重新诠释合作原则，其中每个原则对说话者和听话者都分别提出一定要求。

表1:Levinson的三原则

例如，说话者使用“and”时，听话者往往根据I原则赋予“and”真值联结词以外的意义。比如：John turned the key and the engine started（约翰转动了钥匙，并且引擎启动了）。说话者根据I原则只使用了“and（并且）”，但听话者自动根据情况将“and”的意义拓展理解为强调时间的“and then（然后，随后）”，强调因果关系的“therefore（因此）”或强调目的的“in order to（为了）”。再如自然语言中的许多“if（如果）”其实表达的是“if and only if（当且仅当）”，这也是说话者和听话者使用I原则进行交际的体现。

Levinson的理论同时考虑了说话者编码策略和听话者的解码策略，对“合作”究竟是如何在说话者和听话者之间实现的进行了更为具体和详实的刻画，并着重于描述听话者如何根据字面信息来推测说话者的交际意图，具有更强的适用性和解释力。

Leech（[8]）认为应该用礼貌原则作为对合作原则的重要补充。Leech认为，在会话活动中，还有一种不可忽视的文化力量左右着话语的进行，即礼貌。人们常常会为了礼貌而采取明显有悖于合作原则的话语行为。例如为了给对方留面子而说强度低于自己所知的话（违反量准则），甚至有时说“善意的假话”（违反质准则）或为转移令人尴尬的话题而说一些不相关的话，“顾左右而言他”（违反关系准则）。Leech总结了宽容原则、谦虚原则、同情原则等礼貌原则的子原则，指出这些原则按照自身的方式发挥作用，影响话语的走向与理解。礼貌原则指出决定话语进程的除了信息的传递策略外还有其他因素，如礼貌等社会文化因素。这些因素同合作原则结合起来，共同构成会话行为的内在准则。而针对合作原则本身并非一个形式化理论的事实，Gazdar于1979年在著作《语用学：隐涵、预设和逻辑形式》（[2]）中提出了“语境转化理论”，试图用形式化手段来刻画语境的动态转化机制，并在形式系统处理会话隐涵和预设等问题。

在Gazdar的理论中，一个处理会话隐涵和预设的语用推理模型Π是如下一个六元组：Π=〈fc,fs,fp,D,W,[]〉，其中D是要给出语义描述的对象句子（陈述句）的集合，W是可能世界集。[]是从D到℘(W)的函数，即将每个陈述句指派到一个可能世界的集合上，直观上是该句为真的可能世界的集合，即将D的语义值解释为一个命题。D上有两个函数P和K，直观上表示“可能”和“知道”。这即是说，若φ∈D，则“可能φ”和“知道φ”也属于D，并照常在[]下解释为该句为真的可能世界的集合。

首先需要定义一致的命题集。

定义2.1X⊆℘(W)是一致的，当且仅当，∩X/=∅。

即存在至少一个可能世界，它处于X的每个作为元素的集合之中。这与经典命题逻辑中公式集的可满足性思想一致。

而Gazdar使用以下形式方法定义语境（context）：

定义2.2语境的集合M={X|X⊆℘(W)且X一致}。

即语境是一组可满足的命题构成的集合。而全部可能的话语（possible utterance）定义如下：

定义2.3可能话语的集合N=N×D×M。

一个由自然数n，句子φ和语境X构成的三元组即为一个可能话语。

六元组中的fc,fs,fp分别称为从句数量隐涵（clausal quantity implicature）函数、级差数量隐涵（scalar quantity implicature）函数和预设（pre-supposition）函数。这些函数作用于一个句子，分别得到该句所有可能的（潜在的）从句隐涵、级差隐涵和预设的命题的集合。

fp用于找出一个句子所有可能的预设。设φ∈D，则fp(φ)={ψ|ψ是φ的预设}。例如：

φ=约翰后悔自己没有阻止汤姆的偷窃行为；

ψ=约翰曾经没有阻止汤姆的偷窃行为；

χ=存在一个叫约翰的人；

那么ψ,χ∈fp(φ)。

定义2.4fc(φ)={Pψ,P¬ψ}，满足：(1)对任意句子ψ，有φ=x⁀ψ⁀y，其中x和y是任意可空的符号串，⁀表示符号串的连接；(2)[φ]⊈ [ψ]；(3)[φ]⊈[¬ψ]；(4)对任意α/=ψ，有Kα/∈fp(φ[ψ/α])且K¬α/∈fp(φ[ψ/α])。

这是说，如果ψ是φ的子句子（从句），且φ既不蕴涵ψ又不蕴涵¬ψ，并且如果将ψ替换为α，说φ[ψ/α]并不预设说话者知道α或知道¬α，那么，“可能ψ”和“可能¬ψ”就是φ的从句数量隐涵。

fs用于刻画语句的级差隐涵。

定义2.5fs(φ)={K¬ψai}，满足：(1)φ=x⁀ψai+1⁀y；(2)[φ]⊆[ψai+1]。

这是说，如果ψai，ψai+1构成一组存在级差关系的命题，而一个语言表达式φ中使用了较弱的ψai+1，就意味着φ隐涵说话者知道并非ψai。

fc(φ),fs(φ),fp(φ)分别给出的所有可能的隐涵或预设，实际的预设是将句子φ并入已有的语境M中，考察M和[φ]的一致关系，删除不一致隐涵和预设，保留一致的，最终只有那些一致的隐涵或预设才是真正的隐涵或预设。进而句子φ也称为语境的一部分，进而生成一个新语境M′。随着话轮的进行，不断地有新句子并入已有的语境M中，从而对语境给出了动态的刻画。

Gazdar的理论给出了一个较为精确的形式刻画，并将会话隐涵和预设等问题纳入其中，同时对之前难以用形式方法进行刻画的“语境”给出了一种刻画方案，一定程度上解释了语境变化的过程和机制。但该理论也面临一些问题。首先，该理论将句子解释为命题，用可能世界的集合来刻画。这种做法虽然经典，但忽略了合作原则的核心精神——信息的传递与交互，并可能导致对自然语言进行外延逻辑的简单化处理，而这正是传统形式语义学受到诟病的主要原因之一。比如，在预设问题上，Gazdar将一个命题的预设解释为另一些命题，这就将二者置于同一层面上，与预设是句子获得真值的前提条件（见[12]）的直观不符。其次，Gazdar的模型主要刻画了根据格赖斯量的准则进行的推理，而对质准则、关系准则和方式准则的精神并没有给予充分的体现，因此在理论体系的完整性上存在一定不足。针对这两点不足，本文将尝试站在与Gazdar的模型有所不同的“明示-推理”的角度，在下一章构建一个语用推理模型，使得格赖斯及其后来者提出的若干原则都可以在该框架中描述并展示出来，从而展现出这些语用推理原则的一般功能和特性。

3 一个新格赖斯主义的语用推理模型

3.1 会话框架的基本要素

Sperben和Wilson（[10]）的关联理论认为，语言交际是一个“认知-推理”的过程，即“说话者发出一种刺激信号，使之对交际双方互相显映，通过这种刺激信号，说话人意欲向听话人显映或更加清楚地显映一系列的命题”（转引自[11]），即形成一个“明示-推理”的结构。

直观上，一次简单的会话活动的参与者包括说话人与听话人两方面。说话人说出话语表达式（明示），听话人听到表达式并理解其意义，然后推导出说话人想表达的信息（推理）。即听话人要通过说话人说出的话语来推断说话人知道的信息，例如，假定说话人是诚实的（即遵守“质准则”），那么听话人可由说话人“说X”这一事实推导出说话人“知道X”这一信息。在这一过程完结之后，听话人如有必要，会对说话人给予话语反馈，此时的听话人变成了说话人，而原来的说话人反过来称为听话人，然后重复上图所示的过程。这样说话人与听话人的身份不断互换，不断重复着上述过程，即形成一个个“话轮”，直到一方认为会话已经完结并发出终止会话的信号，对方认可此信号后会话终止。

因此，这里要给出的推理模型要刻画两方面的因素：其一，“谁说了什么”（明示）；其二，“他知道什么”（推理）。

为了实现这一目的，首先需要会话参与者的集合D。因为一般的会话至少应有2位参与者，所以D至少应包含2个元素。

其次，还需要一个对象话语的集合Φ，即说话人在会话中可能用到的所有语言表达式的集合。这一集合的基本元素是陈述句。实际的会话过程可以看作是说话人从Φ中选取语言表达式的过程。Φ中的陈述句可以使用古典联结词进行联结，在日常语言中最常用到的是“并非”和“并且”，分别用加下划线的符号表示。一个或几个可以出现在会话中的陈述句经过联结词作用后，仍是可以出现在会话中的陈述句，因此如果将看作句子间的运算，那么Φ应该是对以上几种运算封闭的集合；另一方面，任何陈述句理论上都可以进行否定、合取等操作，所以，〉就形成一个代数结构，该结构的“论域”是陈述句形式的语言表达式，而各种运算代表句子之间的联结。以后记为Φ。

结构是用于刻画会话语形的工具，说话人每说一句话，就相当于从其中选择了一个元素用于交际。至于如何使用语言基本符号来定义Φ中的元素是什么样子，是形式主义语形学的工作，不是本文讨论的主要内容，因此这里假设Φ是给定的，只需满足古典联结词的代数性质即可，由于本文将问题的讨论范围限制在陈述句领域，所以这一点是在各种语形理论中易满足的。需要注意的是：第一，绝大多数情况下“”的使用并不出现“并且”，事实上将两个句子连续说出，或用一个逗号联结它们，就默认二者之间的逻辑关系是合取（除非句子中明确出现“或者”这种有标记的情况）；第二，这里并不涉及到自然语言实际出现的“并非”“并且”等词汇的意义是否就是逻辑联结词的讨论，而是说，如果表达式中确有起古典联结词作用的语言要素（比如一个逗号联结两个无其他逻辑关系标记的句子），那么形式上就应该用带下划线的联结词进行刻画。

对于Φ中的每个句子φ而言，直观上都有一定的意义或表达一定的信息。这里对所谓的“意义”和“信息”进行一种实体化的理解，即φ表达的意义或传达的信息是某种个体性的对象的集合，即φ蕴含着一定的“信息量”。

设M是Φ中句子的意义或表达的全部基本信息的集合，Φ中的每个句子φ的意义都解释为M的一个子集，直观上该子集中的元素即为φ表达的一组信息。

当句子解释为信息时，什么样的句子表达什么样的信息就会存在主体间的差异，这样，就会存在从Φ×D到℘(M)的解释函数F，F(φ,a)是主体a对φ的语义解释。当具体问题中的a对F(φ,a)的取值没有影响或不关注时，F(φ,a)简写为F(φ)。例如对许多简单的、公共性的话语的理解，不同主体间的差异基本可以忽略。

这种语义处理方式与将命题解释为可能世界的集合的做法（如Gazdar的模型中）是不同的。后者的做法会导致古典联结词解释为可能世界集间的布尔运算，然后形成可能世界集的幂集代数，形成一些如的理论结果。类似的结果在刻画自然语言的意义方面存在的缺陷已经是有目共睹的。考虑这样一个关于预设的例子：

A.约翰后悔自己没有阻止汤姆的偷窃行为。

B.约翰并不后悔自己没有阻止汤姆的偷窃行为。

基于古典否定词，使A和B同时成立的可能世界是不存在的，但这并不等于A和B没有向读者传达任何公共信息。因为“后悔”是一个叙实动词，所以至少A和B共同的预设：

C.约翰曾经没有阻止汤姆的偷窃行为。

是两句话共同传达的信息。无论说A还是说B，说话者都将C的信息传达给了听话者。

因此，在“信息量”的语义解释下，并没有。这就使得这种处理方式更为贴近自然语言的实际使用。例如在预设问题上，如果认为预设是句子获得真值的前提条件（[12]），那么预设的信息就应该在之中。

类似地，基于可能世界集的语义解释有，但这里并不一定有，因为将两句话同时说出所表达的信息往往多于两句话分别表达的信息之和，即产生“一加一大于二”的“言外之意”。（详见3.4节）

但这并不意味着这里要取消联结词在语义值的组合性上发挥的作用。联结词的语义解释仍是表达式语义值之间的函数，并满足一些性质，只不过这个函数不是简单的布尔代数。

不过，一个解释函数F函数还是应该满足下面定义的信息合取基本性质：

定义3.1.1(信息合取基本性质)

设解释函数F，则F有信息合取基本性质，当且仅当F满足：。

该关系保证了合取的基本性质，即“说得越多，表达的信息就越多”。φ表达的信息在添上ψ后依然存在，只是并不保证ψ带来的新信息能与φ原有的信息保持一致，此时就需要听话者进行推理和取舍。不过这种情况并不包括ψ是对φ的更正或取消，因为此时二者的关系不是∧。

考虑到自然语言的句子往往有歧义现象，为了简明起见，这里假设Φ中的每个句子φ的意义都没有歧义，或都已经通过重音、语境、背景知识等外部手段排除了歧义。

同时注意到，℘(M)中的“意义”或“信息”之间存在Horn级差衍推关系“⇒”，即同一语义场的一组强度不同的表达式构成的表达式序列形成的衍推关系。例如：

例3.1.2

1.F(所有人喜欢玛丽)⇒F(有人喜欢玛丽)

2.F(明天上午必然有语文课)⇒F(明天上午可能有语文课)

3.F(公民应该依法纳税)⇒F(允许公民依法纳税)

4.F(张明吃了三个包子)⇒F(张明吃了两个包子)

⇒F(张明吃了一个包子)

即⇒是一个℘(M)上的二元关系。直观上，该关系具有传递性。为了理论方便，这里要求该关系是禁自反的。这并不是说，一个Horn层级的命题无法推出其自身，而是要求在用⇒刻画Horn级差时，避免出现一个表达式自身的Horn层级高于自身的情况。这样，⇒是一个严格偏序。

当两个意义之间存在级差衍推关系时，我们也常说表达该意义的句子也存在对应的衍推关系，因此如果对a而言有“φ级差衍推ψ”，实际上说的是F(φ,a)⇒F(ψ,a)。这样，级差衍推就分为语言（语形）层面的和信息（语义）层面的。在本文中，符号“⇒”总是表示信息层面上的Horn层级推演关系。

⇒关系在此模型中是作为经验内容或“赋值”而给定的，不过，但同一语言共同体内主体间的差异是相对较小的。一组信息能否在Horn级差的意义上衍推另一组信息，结论应当是公共性的话语知识，故讨论这一问题时可以暂时忽略D的影响。虽然不同的主体有可能将同一句子解读为不同的信息，但如果他们将其解读为同一组信息，那么该组信息能否在Horn级差的意义上衍推另一组给定的信息，答案应该是一致的。故在此模型中没有考虑为⇒加上一个表示主体差异的下标。

但是，当讨论语言层面的衍推关系时，就有可能出现一种“错位”的情况：设F(φ,a)=A/=F(φ,b)=C，F(ψ,a)=B/=F(ψ,a)=D，但有可能A⇒B且C⇒D均是成立的，这样，虽然a和b对φ和ψ的意义理解均不相同，但命题“φ级差衍推ψ”在a和b看来均是正确的。这表面上看是某种“错误”或“误打误撞”，但事实上却并不尽然，因为“衍推”强调的只是关系本身。每个人不可避免地按照自己的方式理解句子，很难保证对句子“内容”的理解一定相同，但如果理解出的不同“内容”恰好各自同时具有衍推关系，那么这两个句子具有该关系这一点毕竟是一个两人公认的事实。也就是说这种“错位”并不会影响这两个句子及其信息间的关系，或者说两人之间依然保持了某种“同构”。因此，说句子层面的“φ级差衍推ψ”，实际上指的是，对任意x∈D，有F(φ,x)⇒F(ψ,x)。由于离开语言是无法表达的信息的，所以3.6节给出的形式语言正是基于句子层面的这种关系。

⇒应满足如下性质：

定义3.1.3(级差衍推基本性质)

1.信息性：任给A,B⊆M，如果A⇒B，且F(φ,a)=A，F(ψ,a)=B，那么F(ψ,a)⊆F(φ,b)。

2.公共性：存在a∈D，F(φ,a)⇒F(ψ,a)，当且仅当，对任意a∈D，F(φ,a)⇒F(ψ,a)。

3.传递性：如果A⇒B，B⇒C，那么A⇒C。

4.禁自反性：并非A⇒A。

至此可以得到用于刻画会话过程中信息表达与传递的框架。

定义3.1.4一个会话框架是一个五元组〈D,Φ,M,⇒,F〉，其中：

1.D是会话主体集，2≤|D|＜ω；

2.是会话语言结构；

3.M是会话语义集；

4.⇒是℘(M)上的级差衍推关系；

5.F是会话语言的解释函数。

该框架由会话参与者、话语形式与话语意义三个层面构成。对每个会话者而言，一定的话语形式表达一定的话语意义或信息，而信息之间存在语义上的衍推关系，会话参与者以信息间的衍推关系为基准，通过合作原则等语用原则生成和构建语用推理。这种推理的表现形式为，通过说话者使用的语言形式，来推知说话者知道的信息。这一过程需要通过会话进程和会话信息状态来进一步刻画。

3.2 会话进程、信息状态与质准则

会话框架〈D,Φ,M,⇒,F〉涉及语言、意义、意义间的关系及主体对意义的理解。一次真实的会话活动在此框架上有序地展开。一次会话表现为话轮的交替和说话者与听话者的角色互换。形式上可以这样刻画一次会话：

定义3.2.1一次基于会话框架〈D,Φ,M,⇒,F〉的长度为n的会话是如下一个函数：∆:Nn→D×Φ。

其中Nn={x∈N|x＜n}。∆(n)=〈a,φ〉表示这个会话中过程的第n+1句话（因为第1句话是∆(0)）是a说的φ。这里自动排除了不同的说话者“抢话说”或“同时说”的情况，因为这并非会话交谈的典型方式。

人总是基于一定的信息进行会话活动。信息自身是公共性的，相同的信息可被任何主体以某种方式获知。每个主体在自身的知识范围内都掌握着一定的信息，不同的主体掌握的信息既有交集，又有不同。因此会话活动中的人必须“知道些什么”，即在说每一句话之前，一个人存在一个信息的集合，即M的子集，该集合是他“知道的东西”。会话开始之前，该集合的内容是人掌握的“初始信息”，随着会话进程的推进，该集合发生变化，其中的内容可能会增加或减少。

给出该集合中的所有元素是不可能也不必要的，因为人所拥有的信息不可能时刻浮现在自我意识当中，使得我们有一种方法将其全部表示出来。因此这里的关注点是，给定一组话语表达的信息F(φ,a)，确证其是否包含在a的信息库当中。

定义3.2.2一次基于会话框架〈D,Φ,M,⇒,F〉和会话∆的会话信息状态E是如下一个函数：E:Nn+1×D→℘(M)。

F(φ,a)⊆E(n,a)表示在第n+1句话被说出之前，对a而言他掌握了φ的信息。举例来说，F(我生病了)⊆E(3,张三)表示这个会话中过程的第4句话开始前，“我生病了”传达的信息在张三的信息库当中。而E(0,张三)表示张三在此次会话开始前的信息“初始状态”。

话语内容与说话者的信息库是不断相互影响的。∆与E的互动关系如下表所示。

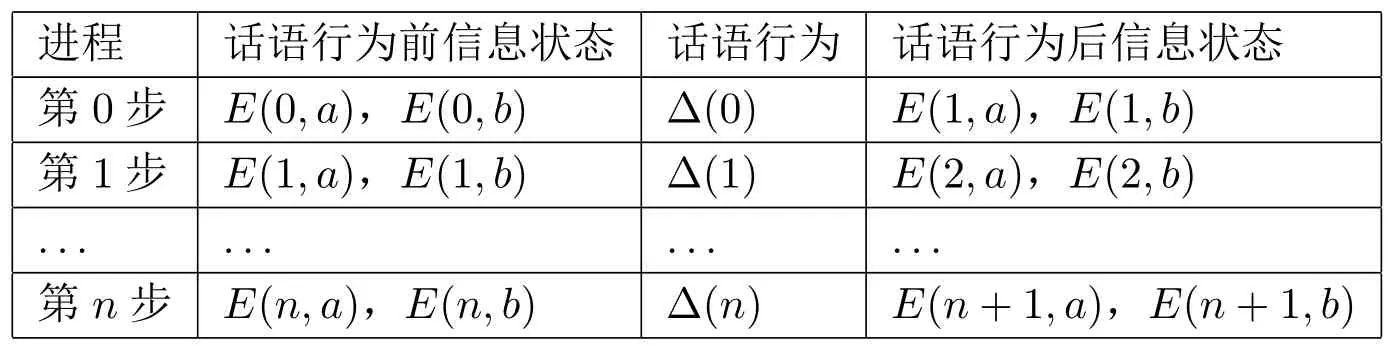
表2:∆与E的互动关系

一个话语行为∆(n)如何呈现，取决于说话者a说此话前的信息状态，或者说，∆(n)的形式取决于E(n,a)的内容。在实际的交际中，人们所做的事情正是如此——通过对方说了些什么，来揣测对方知道些什么，对方在想什么。因此，在此框架中，语用推理的实质是：通过a的话语行为∆(n)，来反推E(n,a)中的某些内容。

最简单的一种反推方式就是依据合作原则中的“质准则”。质准则的要点是，说话者应该在自身的知识范围内说自认为真的话，即说出此话时，该句话包含的信息应全部包含在说话者的信息库中，即：

定义3.2.3(质准则)

如果 ∆(n)=〈a,φ〉，那么F(φ,a)⊆E(n,a)。

亦即说出的内容应在说话者的信息状态集中找到依据。假设a明知φ是假的，或不知道φ是否为真，那么就意味着φ的信息或语义值F(φ,a)不完全在a说话时的信息集E(n,a)中。如果此时a说φ，就违反了质准则。

3.3 衍推链与量准则

根据Horn级差理论，说话者在级差的链条上应选择自知的最强的项进行表达；不使用更强的项就意味着无法使用该项。例如，在“有些-全部”的级差关系中，如果说话者使用“有些学生喜欢文学”，那么就意味着他知道并非“所有学生喜欢文学”，或至少不知道是否“所有学生喜欢文学”。也就是说，在级差衍推关系⇒的线形链F(φn,a)⇒F(φn-1,a)⇒···⇒F(φ0,a)上，如果a使用了某一项F(φi,a)的语言表述φi，那么就有任给j＞i，F(φj,a)不在a的信息掌握范围之内，因为φj比φi更强。

这样就在级差链条的基础上对Horn的Q原则和Levinson的Q原则都进行了刻画：

定义3.3.1(Q原则/量准则) 如果∆(n)=〈a,φ〉且F(ψ,a)⇒F(φ,a)，那么F(ψ,a)⊈E(n,a)。

F(ψ,a)⊈E(n,a)这一事实正是a说φ而引起的会话隐涵的内容。

例3.3.2

φ1=一些学生出席了会议

φ2=大多数学生出席了会议

φ3=全部学生出席了会议

三句话存在Horn级差关系：F(φ3,a)⇒F(φ2,a)⇒F(φ1,a)。若a在会话中的某一步n说了φ2，即∆(n)=〈a,大多数学生出席了会议〉，可由命题3.3.1知F(全部学生出席了会议,a)⊈E(n,a)，即使用“大多数学生出席会议”意味着a的信息库不支持“所有学生出席会议”，这即是典型的级差会话隐涵推理。

该原则常常与质准则一同发挥作用，从而用简易的表达式来传达精准的信息。例如，当我们针对某一数量进行断言时，常常可以根据数量之间的衍推链推知同样的断言对于其他数量是否成立。

例3.3.3φ=有五名同学出席了会议。

正常情况下，如果a说了φ，即∆(n)=〈a,φ〉，那听话者一般会理解为，数量“五”是a所知的信息的最大值。这样，一方面，根据质准则，有F(φ,a)⊆E(n,a)；另一方面，由于存在着关于数量的Horn级差链：

···⇒F(有六名同学出席了会议,a)⇒F(有五名同学出席了会议,a)⇒···⇒F(有一名同学出席了会议,a)，

所以，根据量准则，有如下推理：

类似地，“有七名”“有八名”……等“更多的同学出席会议”均不在a的信息库E(n,a)中，因此可得：

对于1≤n≤5，F(有n名同学出席了会议,a)⊆E(n,a)；

对于n＞5，F(有n名同学出席了会议,a)⊈E(n,a)；

因此，虽然a只说了“五名同学”的情况，但其他人却可以根据以上两点全面地推知对任意n，“有n名同学出席了会议”是否是a所掌握的信息。这与日常推理的一般情况是相符的。

3.4 相关性与信息原则

话语内容的相关性是一个较难描述的性质。为了说这一特性，有必要首先来将“相关”与“不相关”进行对比。

例3.4.1

A1.李明生病了。 B1.李明生病了。

A2.李明是大学生。 B2.李明感觉很难受。

C1.李明生病了。 D1.李明生病了。

C2.李明吃了不干净的食物。 D2.李明坚持工作。

直观上，A组的两个句子表达的信息是相关性最差的。为了说明这一点，我们尝试将A、B、C每组中的两个句子放入同一语境中来解读。最简单的方式就是使用逗号将二者联结起来：

例3.4.2

A3.李明生病了，李明是大学生。

B3.李明生病了，李明感觉很难受。

C3.李明生病了，李明吃了不干净的食物。

D3.李明生病了，李明坚持工作。

不难看出，A3的连贯性是最差的。事实上，从传达信息的角度来讲，A3的两个分句传达的信息仅仅是它们自身信息的加和，从中我们只能知道李明的健康状况是“生病”以及李明的身份是大学生，而这分别是A1和A2传达的信息，即F(A3,a)=F(A1,a)∪F(A2,a)。而后三组则不然，它们在分句自身的信息之上还附加了新信息。B3不仅包含李明的健康状况和身体感觉，更重要的是强调二者之间的关系，即“‘李明感觉难受’是‘李明生病’的结果”，而这一信息既不包含于B1也不包含于B2，而是在B1与B2组合成B3后新产生的，即F(B3,a)⊃F(B1,a)∪F(B2,a)（⊃表示“真包含”）。再如C组，C1表述了李明的健康状况，而C2只是陈述了李明之前做过的一件事情，但C3表达的因果关系“因为李明吃了不干净的食物，所以李明生病了”这一信息是额外产生的。该因果关系是关系准则所要求的。假如事实上李明的生病同他吃不干净的东西之间毫无关系，那么可以断定C3的说话者违反了合作原则。而D组中产生的新信息则有关于李明的某种道德品质，而该李明具有品质无法单独从“李明生病了”或“李明坚持工作”中单独推知。

因此，相关性的意义在于，当人们把两个句子放入同一语境之中时，这两个句子产生的信息不再只是它们自身单独包含的信息的并，而是额外产生某些新信息。而没有相关性的句子就无法产生这样的功效。事实上会话者的关注点往往正是这些新信息。

这样可得相关性的定义：

定义3.4.3φ与ψ对a而言是相关的，当且仅当，

使孤立的句子形成语篇的最简单的方法就是将它们连续说出。当不加任何标记地说出一连串陈述句时，总是默认句子之间的逻辑关系是合取。所以例3.4.2中逗号的作用就相当于用古典合取联结词将两个句子联结起来，因此此定义中的正是基于这样一种考虑，它的意义在于使孤立的句子联合成为语篇，从而获得产生新信息的可能性。而这正体现了Horn的R原则和Levinson的I原则的精神-用少的话语产生多的信息。

也就是说，关系准则的要求是，当两句话放在一起时要“产生一些新信息”，并将人们的关注点集中到这些新信息上来。具体产生什么样的新信息，则要取决于说话者的知识与经验。这一定义抓住了Levinson的I原则的形式特点，即听话人总是根据字面信息而拓展和推知额外的信息，即中的元素。这就意味着，a在说出ψ时，信息就应该已经在a的信息库中，即可以根据关系准则提供这样的担保：如果产生新信息，那么该信息一定是a所掌握的。因此，可以得到：

定义3.4.4(关系准则)

如果

该准则是说，如果b在第n步说了φ，而a在之后的第m步说了ψ，那么，如果a遵循关系准则，那么a保证由φ和ψ合取而可能产生的新信息在m步开始时是自己掌握的。例如，如果a在“李明生病了”之后说出“李明坚持工作”，那么由两句话联立产生的新意思“李明因带病工作而具有某种品质”是a在说出“李明坚持工作”时就已掌握的。有了关系准则，我们便可要求说话人对自己话语可能产生的言外之意“负责”。

3.5 关于方式准则

格赖斯的方式准则要求说话者采用清楚明白的说话方式，与之相关的Levinson的M原则也做了类似的要求，即说话者应当避免无故使用有标记的表达式。也就是说，为了传递特定的信息，说话者在各种能够表达该信息的语言形式中根据某些要素进行选择，从而选出方式最恰当的语言形式。设I⊆M是说话者要传达的一组信息，那么说话者做出的选择就是在集合{φ∈Φ|I⊆F(φ,a)}中选出一个元素。即存在某个选择函数H，使得H({φ∈Φ|I⊆F(φ,a)})就是说话者按照方式准则选出的恰当的表达式。

影响选择的重要因素之一是φ的形式本身。表达式的长度、语法结构的复杂度和词汇的难度很大程度上决定了一个表达式是否成为优选项。一般说来相对简单的表述更容易被人们接受。但是，根据会话目的的不同，并不一定总是形式上最简单的表达式才是最符合方式准则要求的表达式。例如正式场合中的语言并不是越简单直白越好。另一方面，Leech等人提出的礼貌和面子问题也制约着表达方式的选择。人们为了维护自己或他人的面子，而采用委婉复杂的话语形式也十分常见。甚至在很多情况下，说话者的情感、意志、身体状况等非理性因素也在很大程度上影响着话语选择。

因此，具体分析不同的语言环境和交际目的对H的要求应是一项专门的课题，在本文给出的模型中无法详细展开。

3.6 基础会话推理系统

基于以上对会话框架和话语进程的讨论，此处给出一个形式语言L来刻画上述模型中的某些性质和推理事实。

定义3.6.1(L的语形)

1.设D是表示会话主体的符号集是会话语言结构，L的初始符号包括：(1)所有D中的会话主体符号；(2)所有Φ中的对象话语符号；(3)所有n∈N；(4)“说”：S；(5)“知道”：K；(6)级差关系词：＞；(7)联结词：¬，→；(8)辅助符号：(,)。

2.L的公式定义如下：

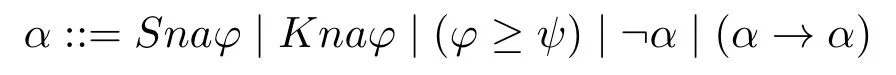
其中a∈D，φ,ψ∈Φ，n∈N。

3.被定义逻辑符号∧、∨、↔的定义如常。

定义3.6.2(L的语义)

设F=〈D,Φ,M,⇒,F〉是一个会话框架，∆是一次会话，E是此框架下该次会话的信息状态。

1.三元组〈F,∆,E〉称为一个模型。

2.满足关系“”：

3.公式α是有效的，当且仅当，任给〈F,∆,E〉，都有〈F,∆,E〉⊨α。

定义3.6.3基础会话推理系统BCIS（Basic Conversational Inference System）

1.公理模式：

2.变形规则：MP

从α和(α→β)得β。

定理3.6.4系统BCIS是可靠的。

证明命题逻辑部分的证明从略，下面只证明Ax.4和Ax.5的有效性。

证明：1.Ax4。任给〉，设，则。根据定义3.1.1对象话语合取词的基本信息性质，有，故故，即

2.Ax5。设，则对任意，故，再由定义3.1.3级差衍推的基本性质 1，；再设，有，故，故，即

3.Ax6。由定义3.1.3，⇒关系的传递性立即可得。

4.Ax7。由定义3.1.3，⇒关系的禁自反性立即可得。 □

直观上，这个语言的每个公式都陈述了一个关于会话或语言的事实或事件：Snaφ表示a在第n步说了φ；Knaφ表示a在第n步知道φ；(φ⇒ψ)表示φ和ψ之间存在级差推演是一个既定的语言事实等。这一语言可以在一定意义上实现基于上述模型的语用推理的符号化与演算化。

3.7 基础会话推理系统的扩张

之前提到的若干合作原则分别表示为：

公式3.7.1

质准则（T）：

量准则（Q）：

关系准则（I）：

它们可以构成一个L-理论。它们的共同点是建立从S类表达式到K类表达式的关系。也就是说，在有这些理论之前，S同K是无关的，即一个人说什么同他知道的信息的关联是不明确的，正是这些理论建立了“明示-推理”间的关联，而探讨这二者的相关性实际上也正是新格赖斯主义的核心任务。

也就是说，本节给出的BCIS是一个讨论语用问题的“基础”或“平台”，是说话人进行会话活动的信息上的“准备”。我们可以在该平台上，通过添加更多公理或规则形成不同的扩张，以使得系统能够表达和处理更多具体的语用问题。

命题3.7.2

1.〈F,∆,E〉⊨T，当且仅当，若 ∆(n)=〈a,φ〉则F(φ,a)⊆E(n,a)。

2.〈F,∆,E〉⊨Q，当且仅当，若 ∆(n)=〈a,φ〉且F(φ,a)⇒F(ψ,a)则F(ψ,a)⊈E(n,a)。

3.〈F,∆,E〉⊨I，当且仅当，若 ∆(n)=〈b,φ〉且 ∆(m)=〈a,ψ〉（n＜m）

则。

该命题与定义3.2.3，定义3.3.1和定义3.4.4的三条原则对模型性质的要求一致，并为加入T、Q、I的扩张系统在相应模型类上可靠性的证明提供了依据。如果将以上三条公式作为新公理，可得扩张的系统BCIS+TQI，该系统默认说话者都遵循以上三条会话原则。

在其他可以考虑继续增加新的公理中，下面的公式是十分重要的：

公式3.7.3

当b=a时，它刻画了a自身话语行为与信息库的继承性和连贯性；当b/=a时，它表明b将a的话φ“听进去了”，当然是基于b自己对φ的意义的理解。在∆与E的互动过程中前文关注的方向在于E(n)→∆(n)，而该公式刻画了在∆(n)→E(n+1)关系中的信息传递与继承的基本关系。此公式不是有效的，即逻辑上允许a说了φ，b还不知道φ的情况，但该公式表达了话语行为的直接效果，一个强调信息交互的语用推理理论应将此公式作为该理论的公理。

由定义易证得如下命题（证明从略）：

命题3.7.4，当且仅当，如果则。

该命题表明了一个模型满足公式3.6.5所需的条件。至此可得另一个扩张系统BCIS+H。该系统通过“说”与“知道”的关系来刻画了“听”。听话人有效地“听”到了一句话，是指他将该句话的信息按自己的理解添加到自身的知识库中。当然，如果该信息与自身已有的信息发生了不一致，那么听话人很有可能会根据其他机制进行一系列后续的筛选和处理，以维持自身信念的一致性。

再如，如果根据某一理论要求说话者信息库中的内容不能导出形式矛盾，可以添加：

公式3.7.5Con：¬(Knaφ ∧Kna(¬φ))。

该公理对说话者的信念一致性提出了要求，或者说对φ和表达的信息的关系做出了某种限制。根据定义，该限制在模型上表现为要求“如果，那么”（即）。再如，以上讨论问题的视角是从某人说什么到他知道什么，即用一种研究者的描述性语言来刻画会话中的事件，但也可以反过来，从说话者知道什么来要求或限定他（不）会说什么，例如：

公式3.7.6。

这是说，如果a说话前已经知道并非如φ那样，那么他不说φ。这可以看做是质准则的另一种体现，是对说话者实施理性话语行为的某种要求。注意它不是先前给出的质准则的逆否。根据定义，该公式对应于性质“如果F(¬φ,a)⊆E(n,a)，那么”。它可以看成是质准则的一种补充，扩充到BCIS+TQI之上，得到BCIS+TQI+T2。

此外，还可讨论话语进程中的某些问题。比如，¬(Snaφ∧S(n+1)aψ)要求研究者用此语言对话语进程的刻画应严格遵循“说话轮流交替”的形式要求，不允许同一说话者占有n和n+1两个步骤。即如果他说了较多句子，刻画时一律如前文所述用∧联结起来。再如，Knaφ→Kmaφ（对任意n＜m）刻画了信息的单调性，即说话者总是“固执且不健忘”的，他可能会随着话语进程知道更多的信息，但不会删除或忘记自身之前的知道的信息。当然，如果结合公式3.6.5和3.6.7，就有可能遇到说话者获知的新信息与自己已有信息相矛盾的情形，这就需要其他机制帮助说话者对具体信息进行筛选和判断，从而保持自身信息的一致性，如在非单调推理研究中著名的“鸟会飞”的例子等。（参看[13]）

可见，在本文提出的模型的基础上，尚有一个十分广阔的问题讨论空间。本节提出的几个扩张的系统只是一些例子，研究者可以根据实际情况，在以上提出的T、Q、I、H、C、K、T2等公理中进行组合和选取，或继续提出新公理，来构成BCIS系统的许多不同扩张，从而适应解决不同问题的需要。

4 结论与总结

基于“明示-推理”的话语交际模式，本文采用了〈D,Φ,M,⇒,F〉作为会话活动的语形-语义基本框架。该框架由会话参与者、话语形式与话语意义三个层面层面的要素构成，从“话语传递信息”的角度来理解句子（陈述句）的语义值，将句子解释为该句相对于某主体而言表达的一组信息的集合，从而避免了Gazdar等人将句子解释为可能世界集的传统做法在处理自然语言时的某些问题。当然，这并不意味着说话人说出的话没有了真值或真值条件，而是说，这里将关注的重点由利用某种装置（如可能世界）给出说话人所说的语句的真值条件，转向了说话人的话语行为带来的认知和推理结果的刻画上。或者说，本文给出的逻辑系统是关于话语行为而非话语内容的。

在如何描述会话进程的问题上，本文认为一次实际的会话活动表现为说话者交替发出的话语序列∆，而决定∆内容的主要因素是说话者掌握的知识或信息E，话语交际活动实际上是∆与E的互动过程，语用推理活动的实指是通过话语的表现形式∆来推知说话者掌握或想传达的信息内容。

格赖斯和新格赖斯主义者提出的合作原则及其各种补充，实质上都是希望给出一些一般性的规则，来完成通过a的话语行为∆(n)，来反推E(n,a)中的某些内容的工作。格赖斯和新格赖斯主义提出的若干原则在上述会话推理模型中的意义可以用形式化的方案给出。而与话语表达方式有关的方式准则（M原则）则有用表达一组公共信息的句子集上的选择函数以某种方式实现的可能。

在此基础上，可以给出一个如3.6节所述的形式语言L。该语言的每个公式解释为该模型上各要素间的关系，直观上都陈述了一个关于会话或语言的事实或事件，进而构建了基础会话推理系统BCIS，从而帮助实现对模型上的会话活动进行某种程度的符号化和演算化的刻画。

[1]P.Brown and S.C.Levinson,1987,Politeness:Some Universals in Language Usage,Cambridge:Cambridge university press.

[2]G.Gazdar,1979,Pragmatics:Implicature,Presupposition and Logical Form,New York:Academic Press.

[3]P.Grice,1975,“LogicandConversation”,inP.ColeandJ.Morgan(eds.),SyntaxandSemantics,pp.41-58,New York:Academic Press.

[4]L.R.Horn,1972,On the Semantic Properties of the Logical Operators in English,Indiana:Indiana University Linguistics Club.

[5]L.R.Horn,1984,Toward a New Taxonomy for Pragmatic Inference:Q-Based and R-Based Implicature,Washington D.C.:Georgetown University Press.

[6]J.J.Katz,1971,The Underlying Reality of Language and Its Philosophical Import,New York:Harper Torchbooks.

[7]E.L.Keenan,1976,“Towards a Universal Definition of Subject”,Subject and Topic,pp.303-333,New York:Academic Press.

[8]G.N.Leech,1983,Principles of Pragmatics,London:Longman.

[9]D.Sperber and D.Wilson,1981,“On Grice’s Theory of Conversation”,in P.Werth(ed.),Conversation and Discourse,pp.155-178,London:Croom Helm.

[10]D.Sperber and D.Wilson,1986,Relevance:Communication and Cognition,Cambridge:Harvard University Press.

[11]曹晓晶，“明示——推理模式中语境的作用”，文学界（理论版），2001年第3期，第81-82页。

[12]周北海，傅庆芳，“一个关于专名指称存在预设的形式刻画”，逻辑学研究，2014年第1期，第1-12页。

[13]周北海，毛翊，“一个关于常识推理的逻辑基础”，哲学研究，2003年增刊，第1-10页。

[14]周礼全，逻辑——正确思维和有效交际的理论，1995年，北京：人民出版社。