弗封闭策略及相关论争探析*

李珂

南京大学哲学系

like0628@163.com

刘飞

南京森林警察学院基础部

life1985@163.com

双面真理论（dialetheism，以下简称“双真论”）是在亚相容逻辑（paraconsistent logic）研究中提出的一种哲学思想，即在一定意义上承认“真矛盾”或“真值叠加（glut）”的思想。以此为思想背景而构建的逻辑理论称为双真论理论。经过数十年的探讨，主张双真论的学者就如下问题已达成共识：使用以LP（Logic of Paradox）为代表的双真论理论能够较好地解决集合论悖论和语义悖论。一直以来，这被视为LP最独特、最重要的解题功能之所在。但LP的创建人普利斯特（G.Priest）认为，LP理论的应用空间并不限于集合论悖论和语义悖论的范围，比如可借助弗封闭模式（Inclosure Schema）（[4]，第147页）作用于连锁悖论（sorites paradox），从而拓展LP理论的应用领域。他的具体做法是：用弗封闭模式重构连锁悖论，使其与集合论悖论、语义悖论等均被统摄在该模式之下，然后按照“统一解法原理”（PUS：the Principle of Uniform Solution，即“同一种类悖论具有同一种解法”）（[4]，第183-184页）将双真论解悖方案应用于解决连锁悖论。

比尔（Jc Beall）把这一做法称为弗封闭策略（inclosure strategy）（[2]，第829页），但他并不认为该策略能够成功解决连锁悖论，理由之一是弗封闭策略不能解决在本质上与连锁悖论同为弗封闭悖论的寇里悖论（Curry’s Paradox）（[2]，第831页）；另一个理由是弗封闭策略找不到正确的“容忍条件句”（tolerance conditionals）（[2]，第832页）。比尔由此提出了弗封闭策略的替代方案——基于不可断定性算子（unassertability operator）的保持容忍论证（the preserving tolerance argument）。（[2]，第831页）然而，以普利斯特为代表的部分双真论者对比尔的论证进行了多方反驳，从而否认这种替代方案。（[7]）双方为此进行了多轮讨论，尚未就此达成一致意见。鉴于国内学界对于双真论者的这种“内部论争”尚缺乏应有关注，本文拟就这一论争的来龙去脉予以系统评述，并谈谈我们的一些思考。

1 弗封闭模式

普利斯特基于对罗素悖论的重塑，认为弗封闭模式可以概括大多数悖论的特征（[4]，第141-154页）。他借助集合论方法将弗封闭模式建构如下：

对于一元谓词φ和θ，一元函数δ，存在一些明显为真或者先验（a priori）为真的原则，当这些原则蕴涵下列条件时，弗封闭式悖论（inclosure paradox）产生：

1.存在一个集合Ω，使得Ω={x:φ(x)}和θ(Ω)（存在性，Existence）；

2.如果X⊆Ω且θ(X)，那么

(a)δ(X)/∈X（超越性，Transcendence）；

(b)δ(X)∈Ω （封闭性，Closure）。

（关于弗封闭的一种特殊情况是，当θ(X)是空条件，即当X=X时，可能不会被提及。）根据这些条件，在界线处，即当X=Ω时，矛盾产生：δ(Ω)∈Ω且δ(Ω)/∈Ω。此矛盾又被称为弗封闭矛盾（inclosure contradiction）。（[6]，第70页）

普利斯特曾以图1直观地展现了弗封闭模式的原理。

他认为弗封闭模式能够很好地应用于布拉里-福蒂悖论（Burali-Forti Paradox）等集合论悖论和说谎者悖论等语义悖论。（[6]，第70页）关于这两种悖论的双真论解悖方案在双真论者内部基本达成共识，但是这类悖论只占众多悖论类型中很小的一部分。因此，普利斯特希望利用他的弗封闭模式理论将双真论解悖范围扩展到更宽广的领域，其中连锁悖论是一个重要代表。

2 弗封闭模式对连锁悖论的重构

连锁悖论通常表现为：有一系列对象a0,...,an和一个模糊谓词P，存在Pa0和¬Pan，并且紧邻的两个元素在它们的P属性上只有很小的差别，即如果其中一个元素具有P属性，则根据容忍原理（the principle of tolerance），另一个元素也具有该属性。

普利斯特认为弗封闭模式从形式上能够重构连锁悖论。对于上列弗封闭模式而言，令φ(x)是Px，那么Ω={x:Px}；θ(x)是空条件。因为an不在Ω当中，Ω实际上是A={a0,...,an}的一个真子集。于是，存在性成立。如果x⊆Ω，又因为X是A的一个真子集，在A中就必然存在第一个不在X当中的元素，令这个元素是δ(X)。根据定义，δ(X)/∈X。所以，超越性成立。如果X=∅，δ(X)=a0，于是有Pδ(X)；或者如果X/=∅，δ(X)紧随某个X⊆Ω中的元素，根据容忍原则有Pδ(X)。在两种情况下，都得到δ(X)∈Ω，因此，封闭性成立。连锁悖论的弗封闭矛盾表现为：序列中没有P属性的第一个元素具有P属性。在具有P属性的事物界线处之所以产生矛盾，那是由于对角线法（diagonalization）把界线处的元素带出X，而容忍原则却使它留在Ω之内，如图1所示。因此，弗封闭模式可以从形式上刻画连锁悖论。（[6]，第70-71页）

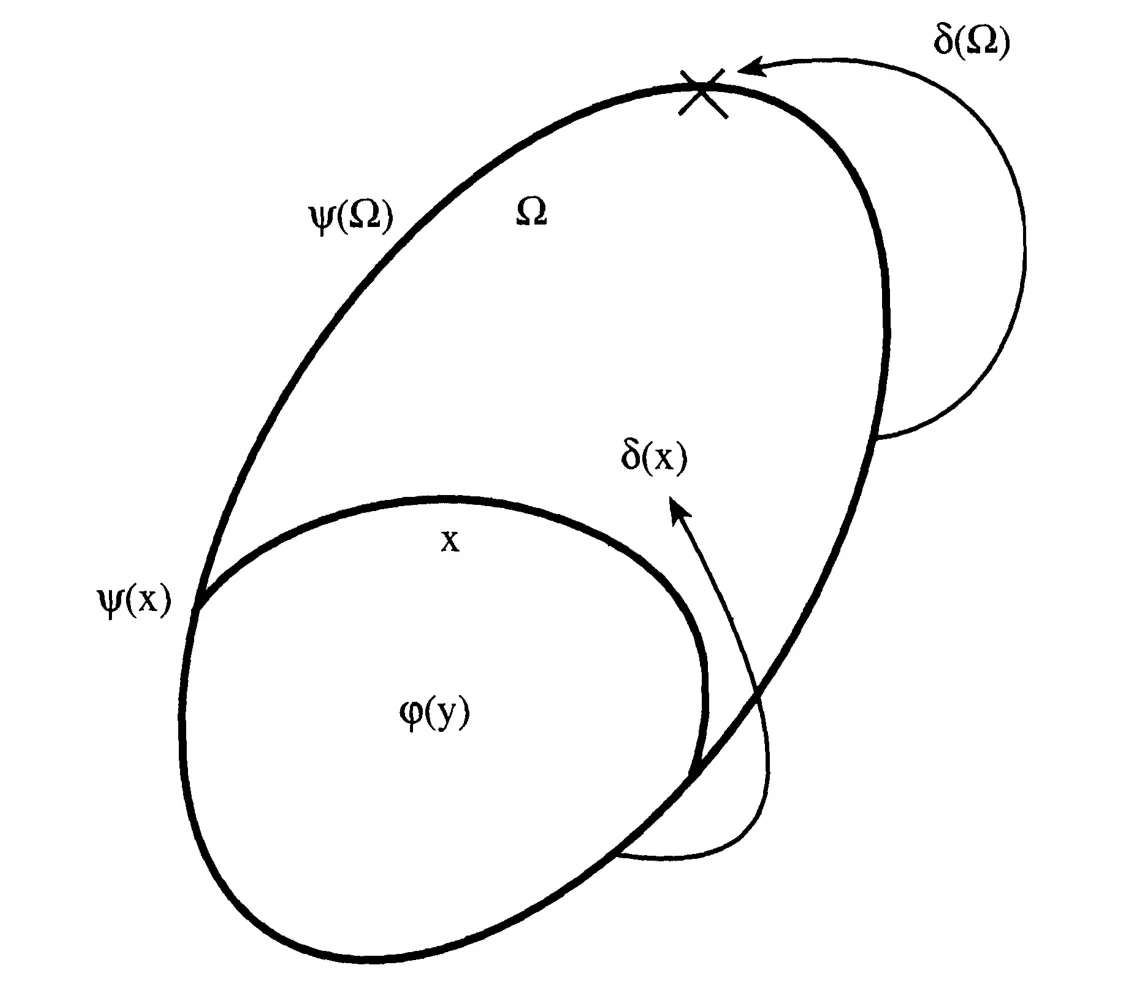
图1:[4]，第172页，图中ψ对应本文中θ，图中x对应本文中X。

请注意，尽管连锁悖论中产生矛盾的点从图1中看似很明确，即产生于界线处，但实际上这个（或这些）点是模糊的。因为连锁论证的相关信息只能推出“矛盾出现在连锁序列起止点之间的某个地方”，但具体位置在哪里并不清楚。而在自指悖论中，产生矛盾的点是界线事例，“出现在弗封闭的界线处，哪一个公式（或语句）是双面真论题（dialetheia）可以被确知”。（[6]，第80页）即便连锁悖论与自指悖论具有这种重要差异，普利斯特仍认为二者同属于弗封闭悖论。他的理由是连锁悖论的模糊性特点与自指悖论的无限扩张状态具有相似性，弗封闭模式能够刻画这两个相似特点。他又通过分析连锁论证的语句联结词、高阶模糊性和界线点（cut-off points）等方面，多方论证弗封闭模式能够刻画连锁悖论。（参见[8]）

3 关于弗封闭策略解悖功能的争论

按照普利斯特等人的设想，双真论者应该都会同意连锁悖论是弗封闭悖论，进而在统一解法原理指导之下采用双真论来解悖。1此处及后文反对比尔的观点来自于包含普利斯特在内的五位双真论者：Z.Weber,D.Ripley,G.Priest,D.Hyde,M.Colyvan。比尔提出反对弗封闭策略的主张后，这五位双真论者开始联合起来为弗封闭策略作辩护。他们被比尔简称为WRPHC，下文皆以“普利斯特等人”代表五位双真论者。然而，同为双真论者的比尔却对此提出了强烈的反对意见。比尔认为，普利斯特的这种“弗封闭策略”对于自指悖论解悖而言是没有问题的，但不能把它扩展至连锁悖论家族。（[2]，第829页）他首先否认弗封闭策略的普适性，最明显的理由是这一策略不能解决寇里悖论，进而也不能解决连锁悖论。（同时，他认为弗封闭策略的相关论证并不充分，该策略不能建构出适合于连锁悖论的容忍联结词，因为它的容忍联结词不具不可传递性和不可分离性的特点；于是，比尔提出了不可断定性理论来寻求正确的容忍联结词。）

3.1 弗封闭策略能否应用于寇里悖论？

比尔以寇里悖论为例否认了弗封闭策略的普适功能，他的论证思路大致如下：寇里悖论虽然适用于弗封闭模式，但如果借助统一解法原理用双真论来解悖就会导致荒谬。（[3]，第800-802页）普利斯特等人的回应是把寇里悖论拒斥在弗封闭模式的适用范围之外，如此一来寇里悖论就不能作为反例对弗封闭策略构成威胁。（[7]，第823-824页）而比尔又采用更为精细的论证来反驳普利斯特等人的观点，认为弗封闭策略会面临一种寇里式的二难困境：“它将‘坏的’寇里事例（cases）排除在外却付出了将太多‘好的’寇里事例也排除在外的代价”（[2]，第846页），这种二难困境的构成可展示如下：

普利斯特等人认定寇里语句是s=〈Ts→A〉，其中A是任意语句。2寇里悖论的语义学版本又称“寇里-吉奇悖论”（Curry-Geach’s Paradox，参见[9]，第100页）请注意区分寇里悖论和寇里语句。在围绕弗封闭策略这一主题展开论争的文章中，双方都没有专门对悖论及相应的悖论性语句作出明确区分，几乎在所有本该涉及“悖论性语句”的时候，不约而同地使用“悖论”进行代替。也许这是一种省略式用法，但更可能的情况是人们不清楚区分“悖论”及“悖论性语句”的必要性和重要性，更不用说明确提出区分二者的标准。（参见[11]）当A是真语句时，该语句模式无法满足弗封闭模式所要求的超越性，此时相应的代入例不属于弗封闭悖论；当A是非真语句时，该语句模式满足弗封闭模式所要求的超越性和封闭性，此时相应的代入例属于弗封闭悖论。按照这种分类标准，如果普利斯特等人的观点“关于寇里悖论的所有代入例——无论A是什么——显然都属于同一种类”（[7]，第823页）当中的“同一种类”指的是“同属于弗封闭悖论”，那么该观点错误。

如果普利斯特等人采用比尔所提出的亚弗封闭悖论案例标准：“当且仅当至少有一个代入例是弗封闭悖论的，那么这种语句模式是弗封闭悖论的”（[2]，第843页），即一般形式下的寇里悖论语句模式（不论A为真语句或非真语句）都属于弗封闭悖论的。这条标准本身及其应用不符合人们的直觉，因为“从特例中得出一般性结论是一种糟糕的形式”。（[7]，第823页）

如果普利斯特等人采用比尔提出的超弗封闭悖论案例标准：“当且仅当所有代入例都属于弗封闭悖论，那么一般形式下的这种语句模式是弗封闭悖论的”（[2]，第843页），即一般形式下的寇里悖论语句模式（不论A为真语句或非真语句）都属于弗封闭悖论的。显然，如果A是任意的，寇里悖论语句模式整体上不属于弗封闭悖论的。要想让寇里悖论严格地属于弗封闭悖论，只能对A加以限制，正如比尔所做的，把A限制为非真语句Au:s=〈Ts→Au〉，或者干脆构造出直接包含否定的“新寇里悖论”：s=〈Ts→A∧¬A〉。（[2]，第843-844页）经过改造，只保留“好的”寇里悖论，将“坏的”排除掉。比尔料想普利斯特等人不会同意这种高度特设的行为，因为其后果是令人难以接受的：一旦人们接受了改造后的寇里悖论新版本属于弗封闭悖论，下面就面临着根据统一解法原理对它们使用双真论解悖方案。而按照双真论，s是既真又假的，那么s可以为真。当s为真时，得出Au为真或者A∧¬A为真。即使双真论者明确承认有的矛盾为真，但是毕竟被承认的真矛盾是有限度的，他们决不可能接受任意Au或者任意A∧¬A成立。也正是在这种情况下，普利斯特等人的观点“关于寇里悖论的所有代入例显然都属于同一种类”才讲得通，因为在这里“同一种类”指的是将寇里悖论的所有代入例看作一个整体，它们“同属于非弗封闭悖论”。

简言之，比尔想尽办法使寇里悖论符合弗封闭模式的刻画从而成为弗封闭悖论，但同时又不适用于双真论解悖方案，使寇里悖论成为弗封闭策略在解悖之普适性方面的典型反例。实际上，他发起进攻的入手点，主要是弗封闭策略的第二个环节——“统一解法原理”（[7]，第823页）：虽然寇里悖论与说谎者悖论等自指悖论一样同属于弗封闭悖论，却不能按照统一解法原理的指导，将成功应用于自指悖论的双真论解悖方案也照搬到寇里悖论上来，可见在这里统一解法原理行不通，至少其所谓的普适性要打折扣。

面对上述挑战，普利斯特等人要想保护自己的弗封闭策略免于陷入不利境地，就必须破斥上述二难推理。他们的解题路径是将寇里悖论彻底排除在弗封闭悖论的范围之外，使之与弗封闭策略无涉。在实际的论证过程中，他们使用的方法是：一方面接受上文中比尔提出的超弗封闭悖论案例标准，但另一方面拒绝对其中的A语句进行限制和修改，即坚持认定包含任意语句A的寇里悖论s=〈Ts→A〉是寇里悖论的唯一一种正确形式，否认其他所谓的“新寇里悖论”等，并在此意义上根据超弗封闭悖论案例标准，将寇里悖论整体排除在弗封闭悖论范围之外。

不难发现，双方争论的关键在于“到底什么是寇里悖论”（参见[5]，第83-84页）。由于对该问题的不同认识，导致了各自对“弗封闭策略能否应用于解决寇里悖论”作出了相反回答。

3.2 弗封闭策略能否应用于连锁悖论？

也许有人会产生疑问，本文所要探讨的一个核心内容是弗封闭策略与连锁悖论的关系，但为什么先要花费笔墨分析关于寇里悖论的论争？下面很快就会发现，关于寇里悖论的论争可以很自然地过渡、延续到对连锁悖论的论争。

如前所述，普利斯特等人没有被比尔说服，坚持认为寇里悖论不是弗封闭悖论，从而保护弗封闭策略免遭寇里悖论的困扰。此时比尔没有采取直接对抗的方式，而是因势利导，先假设“普利斯特等人对弗封闭策略的辩护在寇里悖论那里行得通”，然后据此论证“与此同时，普利斯特等人的辩护也使得关于连锁悖论的弗封闭策略受到了暗中破坏”。（[2]，第846-847页）比尔此处的论述路径，是借助连锁悖论与寇里悖论的相似之处，迫使普利斯特等人承认：当且仅当寇里悖论不是弗封闭悖论，连锁悖论也不是弗封闭悖论。这样一来，普利斯特等人就不得不进一步承认，弗封闭策略失去了贯彻统一解法原理使用双真论解决连锁悖论的关键理由，从而得出该策略不能应用于连锁悖论这一结论。须知，普利斯特等人的初衷恰恰是将连锁悖论作为能够成功应用弗封闭策略的一个新典型，并以此为契机拓展弗封闭策略在传统自指悖论之外的使用范围。简言之，比尔的反驳理路是：如果在普利斯特等人关于“寇里悖论不是弗封闭悖论”的辩护可以使其弗封闭策略免于“下油锅”，那么被比尔认为“同理可得”的关于“连锁悖论也不是弗封闭悖论的”的论证可以又将之推进“火坑”。比尔所谓的“同理”主要指的是寇里语句s=〈Ts→A〉中的语句A的真值具有任意性，这和连锁悖论中连锁序列所包含的任一对象并不必然与起始对象具有矛盾的属性，在本质上具有相通之处，具体表现为：在上述两种悖论中并非所有代入例都是“危险的代入例”，即产生矛盾、进而能够使相应悖论名至实归的代入例。

当然，普利斯特等人不会轻易就范，他们指出比尔的“同理可得”得出的是错误的结论。普利斯特等人的关注点在于作为某种事态的悖论所由以形成的界线事例，因为正是在这些界线处矛盾才得以产生、悖态才真正实现；而比尔强调的是虽具有形成悖态的可能或趋势、但尚未明确产生矛盾的对象，可以理解为它们具有悖态的潜在形式而非实现形式。从普利斯特等人的角度看比尔所谓的“非危险的代入例”，它们不会引起矛盾，不符合弗封闭悖论的“超越性”条件，因而不是弗封闭悖论，更一般地，甚至算不上严格意义上的逻辑悖论，因为能够建立矛盾等价式是逻辑悖论必备要素之一（参见[9]，第7页）。

由此观之，普利斯特等人再次排除了比尔企图由两种“悖论”的“非危险代入例”入手、“同理”得出连锁悖论不是弗封闭悖论所带来的对弗封闭策略造成的危害。如果说比尔的确从他刚刚描述的两种情况中找到了若干相似之处，也能讲得通，只不过这种相似之处另有内容，即两种情况下的代入例因不满足逻辑悖论的构成要素而不能成其为严格的逻辑悖论。这也从侧面反映出比尔与普利斯特等人在“逻辑悖论是什么”、“逻辑悖论的基本构成要素”等问题上的不同认识。而彻底澄清这些关键问题之必要性，也由这样的论争得以凸显。

3.3 弗封闭策略的替代方案

概而言之，比尔为弗封闭策略所提出的替代方案，就是以“相容性缺省原理”（the default-consistency principle）（即仅当不存在任何相容性理论能够享有双真论方案的相同优点时才提出双真论方案）（[3]，第792页）为基本指针，为普利斯特等人借助LP理论支持“真值叠加”的外延化路径，找到一种可行的内涵化路径的替代方案，在这一路径上尽可能与经典逻辑相协调，“保持不足以引发质变的微小量变的过程的论证”（[2]，第831页），即他所命名的“保持容忍论证”。其中他所提出的“不可断定性算子”发挥着基本与关键的作用。他认为，相比弗封闭策略而言，它更符合人们的直觉。

由于在连锁悖论中的容忍条件（tolerance conditionals）似乎为真，但是标准连锁悖论的结论及其所有明显的逻辑后承似乎都不是真的，所以，这一替代方案的关键任务就是要找到“正确的容忍条件句”。构成这种条件句的容忍联结词（tolerance connective）应当具有什么特点呢？比尔给出了两条最显著的限制：

(C1)容忍联结词（≡?）作为连锁悖论中包含的为真的容忍条件句的联结词，它不具有传递性，因为在容忍条件句传递封闭中并非每一个条件句都为真。

(C2)容忍联结词也不具有可分离性：对于所有A和B，A≡?B并且A并不能推出B。

比尔认为这两条限制是“正确的容忍条件句”的必要条件，普利斯特等人也同意这一点。（[2]，第832页）以LP理论为代表的双真论终究是一种非经典逻辑，≡lp既不具有传递性又不具有可分离性，它拒斥经典否定的融贯性；而若从“保持容忍论证”的诉求看，却能够将“LP否定”视为一个不可断定算子。令µ是给定的不可断定算子。如果µ像LP理论者所认为的是否定，那么被定义为µ(A)∨B的A⊐B就成了实质条件句。根据人们的一般看法，被如此定义的A⊐B是通过不可断定性得到定义的条件句，而不可断定性不是否定。无论不可断定性是不是否定，被如此定义的⊐既不具有传递性又不可分离。因此，具有不可断定性算子的容忍联结词满足(C1)和(C2)。这正是比尔提出的保持容忍论证的容忍联结词。

比尔指出，“保持容忍论证”致力于与经典逻辑相协调，但也能够享有以LP理论为代表的双真论理论的容忍联结词，尽管它是以不可断定性算子呈现的。特别地，“容忍联结词”用等值句术语刻画为A≡µB，被定义为(A⊐B)&(B⊐A)。普利斯特认为µ是否定，并因此认为≡µ是（在LP当中）按照通常方式（以LP当中的否定和析取）得到定义的实质条件句。比尔认为µ不是否定，并因此认为≡µ不是实质等值句，而是含有基本的不可断定性算子的一种关系。这个算子经由一个标准的包含世界在内的装置在“内涵上”（intensionally）被定义出来的。（[1]，第101-102页）根据双真论者的观点，连锁悖论证明了（在过渡性区域）“真矛盾”存在。但是比尔认为，由于弗封闭策略不能解释清楚为什么在广大的过渡性区域内处处存在着真矛盾，不足以成为支持将双真论应用于连锁悖论的强有力的论证。

普利斯特等人后来对比尔的替代方案的批评主要包括两个方面：一是对比尔的内涵容忍原则提出质疑，特别是可分离的容忍原则；二是揭示比尔方案中的不可断定性算子是模糊不清的。比尔对于弗封闭策略的批评也可以反作用于比尔，他实际上也无法解释清楚在连锁悖论的广大过渡性区域内作为“不可断定算子”的作用情况。比尔本人也承认很难找到解决连锁悖论所需的正确容忍联结词，只不过相比弗封闭策略而言，他的替代方案更有优势而已。论证双方都没有达到令人满意的论证强度，其不充分性主要表现为关键算子（LP否定和不可断定性算子）的含混不清。

4 对论争的思考

普利斯特等人与比尔就弗封闭策略能否解决连锁悖论进行了几个回合的较量。这看似是对一个悖论解法的争论，实则反映了双方对悖论的认识差异很大。随着争论不断深入，核心问题逐渐显露出来，即通过某种论证能否将真矛盾的存在领域从人们已达成共识的、为数不多的集合论悖论和语义悖论扩展至以连锁悖论为典型代表的、更为普遍的本体论悖论。普利斯特等人试图借助弗封闭策略要扩大双真论理论的应用范围，而比尔作为一位仅在语义层面上支持双真论的双真论者，反对用双真论来解决连锁悖论为代表的本体论悖论。双方的争论从更深层面反映了如下两个方面的问题：

4.1 相容性缺省原则：最大程度保持相容性问题

比尔使用了相容性缺省原则作为立论依据，值得说明的是，这一原则被他和许多双真论哲学家所共同接受。我们想着力挖掘的是，作为普利斯特等人弗封闭策略的反对者，比尔的反驳思路的实质是什么？相容性缺省原则到底起什么作用？

根据比尔自己的叙述，不难发现在他心目中双真论解悖方案的主要优点是明确的，即“坚持连锁悖论的所有前提为真，同时根据某种原则避免连锁悖论的荒谬结论”（[3]，第791页）。但是，紧接着的一个问题是：这种优点是双真论方案独有的么？如果存在某种相容性方案能够共享双真论解悖方案的上述主要优点，根据相容性缺省原则，就没有必要假定真矛盾。

于是，比尔沿着这一思路，尝试寻找与经典逻辑相协调的连锁悖论解法，探究是否“在不包含真矛盾的情况下也能够取得这种优点”。（[3]，第791页）具体来说，他摒弃了外延化路径而转向内涵化理论，将普利斯特等人在LP理论中“既真又假的真矛盾”改造为“真却不可断定的对象”。尽管他用于解释作为连锁悖论前提的、一系列条件句中的容忍联结词的不可断定算子被对方诟病为含混不清，在这一点上不比普利斯特的“LP否定”具有更多的优势，但是，面对对手关于不可断定性算子及相关解法的质疑，他并不强烈要求人们必须接受自己的这一方案，而是在向人们介绍了由休斯（M.Hughes）提出的与不可断定性算子相似的不可知道算子（unknowledge operator）及相关解法，说明“人们也可以沿着由其他经典逻辑理论者提出的方法进行思考，而不必接受我提出的可断定性路径。主旨仍在于：我们可以在没有真矛盾的情况下享有（双真论解悖方案的）上述优点。”（[3]，第807页）我们非常赞赏比尔的这种探究方式。尽可能地与经典逻辑相协调，从而最大限度地保持相容性诉求，可以使非经典逻辑探究能够以“最小代价”获得“最大收益”。

4.2 探究内涵化路径：形式逻辑外延化路径的局限问题

尽管关于弗封闭策略尚处于激烈论争之中，但双方在论争中已达成的一些一致意见，可作为进一步对话的基础。比如，大家一致认识到，解决连锁悖论的前提条件之一，是辨识出正确的容忍条件句，而容忍条件句的关键在于找到具有不可传递性(C1)和不可分离性(C2)的正确的容忍联结词。

普利斯特等人所坚持的弗封闭策略，仍然是基于经典形式逻辑的“外延化”路径进行思考的，其模型论仍然属于一种外延化的“集合论语义”。众所周知，普利斯特使用的“外延的容忍原则”指的是通过实质等值句或实质条件句表达的、根据否定和析取得到定义的容忍原则。（[2]，第835页）LP否定只有在遇到“真矛盾”时，才表现出与经典逻辑否定的异常之处，其他情况下均正常使用。而按照上述(C1)、(C2)的标准衡量，从经典逻辑视角出发的实质条件句已从根本上被排除掉了，它在(C1)和(C2)两方面上都不成立。

所以，比尔不得不转而考虑“内涵化”路径，提出一种不可断定性算子，将LP方案下“既真又假”的语句转化为“真但不可断定”的语句，融入了主体相关性的思考，体现了对悖论本身内含的语用学特质的认识。然而，从比尔本人的探究来看，他在把握“内涵”机制时所使用的仍然是外延化的“可能世界”装置，其探究所陷入的困境与这种处理密切相关。最近，张建军通过对“正规模态集合论悖论”的揭示与探究，表明可能世界语义学对“内涵算子”的模型论刻画，实际上与经典形式逻辑的外延化路径一样，都是基于“实体-属性”关联向“实体-实体关联”的“等价还原”；而如何建构不使用这种等价还原、破除对“实体-属性关联”（真正的内涵关联）的遮蔽的模型论，应是合理建构真正的内涵逻辑理论的根本指向。（参见[10]）我们认为，认识到形式逻辑外延化路径的这种根本局限而寻找真正的内涵化途径，或许也是解决弗封闭策略之论争的根本出路所在。

[1]Jc Beall,2009,Spandrels of Truth,Oxford:Oxford University Press.

[2]Jc Beall,2014,“End of inclosure”,Mind,123(491):829-849.

[3]Jc Beall,2014,“Finding tolerance without gluts”,Mind,123(491):791-811.

[4]G.Priest,1995,Beyond the Limits of Thought,Oxford:Oxford University Press.

[5]G.Priest,2006,In Contradiction:A Study of the Transconsistent,Oxford:Oxford University Press.

[6]G.Priest,2010,“Inclosures,vagueness,and self-reference”,Notre Dame Journal of Formal Logic,51(1):69-84.

[7]Z.Weber,D.Ripley,G.Priest,D.HydeandM.Colyvan,2014,“Toleratinggluts”,Mind,123(491):813-828.

[8]王文方，“论Priest对Sorites悖论的模糊解悖方案”，逻辑学研究，2011年第2期，第35-51页。

[9]张建军，逻辑悖论研究引论，2014年，北京：人民出版社。

[10]张建军，“正规模态集合论悖论及相关问题”，逻辑学研究，2017年第3期，第35-57页。

[11]张建军，“再论‘广义逻辑悖论’的基本构成要素”，南国学术，2018年第1期，第32-47页。