坡地喷灌水滴直径与动能强度分布规律研究

张 林 惠 鑫 陈俊英

(1.西北农林科技大学水土保持研究所， 陕西杨凌 712100； 2.西北农林科技大学水利与建筑工程学院， 陕西杨凌 712100)

0 引言

喷洒水滴直径及打击动能是喷灌系统评价的重要指标[1-3]，水滴直径较小时，喷灌水滴受风的影响较大，易蒸发，从而影响灌溉质量；水滴直径过大，落地时的打击动能较大，易导致土壤表面结皮，影响土壤水分入渗，促进地表产流，造成水、土、肥流失。因此，研究喷洒水滴及打击动能分布规律，对喷头开发和喷灌系统设计具有重要作用。

目前，水滴直径测试手段越来越先进，已由过去的面粉法、滤纸色斑法、浸入法和照相法发展到现在的激光雨滴谱仪法[4-6]。随着技术进步，不仅能实时记录水滴直径，而且还能同时获得水滴速度和落地角度等更多水滴信息。利用水滴的这些信息，国内外学者对喷洒水滴直径分布和打击动能问题进行了大量研究，重点分析了影响水滴直径分布的关键因素，指出工作压力对水滴直径分布影响最大[7]。针对不同类型喷头，建立了水滴直径与工作压力、喷头转速、喷嘴直径和喷头距离等之间的函数关系[8-9]。并依据单喷头水滴运动特性，总结出水滴直径、速度及落地角度沿射程分布的规律[10-11]，揭示了喷洒水滴形成机理[12]。在喷洒水滴打击动能方面，研究了水滴打击动能的空间分布及影响因素，建立了水滴动能强度分布与喷嘴形状等因素之间的数学关系[13-16]。分析了喷洒水滴打击动能对土壤表面结构的破坏程度，得出土壤入渗能力随着水滴打击动能的增大而降低的结论[17-18]。前人的研究对喷头开发和结构改进以及喷灌系统设计都具有重要作用，然而以往研究主要集中于平地喷灌，对坡地喷灌研究相对较少。受地形影响，坡地喷灌更易产生地表径流，造成土壤侵蚀。因此，坡地喷灌水滴直径及动能强度分布规律研究对于坡地喷灌系统设计具有重要意义。

本文以农田灌溉中常用的雨鸟LF1200型喷头为研究对象，在室内无风条件下，应用视频雨滴谱仪实时监测不同坡度下水滴直径和速度等信息，研究不同坡度下水滴平均直径及直径频率沿射程方向的变化规律，分别建立平均直径、速度与坡度等之间的关系，以此为基础，提出无风条件下坡地喷灌打击动能强度计算模型，并应用模型重点分析不同喷头布置方式、间距和坡度对组合喷头打击动能强度分布的影响。

1 材料与方法

1.1 试验装置

试验在西北农林科技大学中国旱区节水农业研究院灌溉水力学实验厅进行。试验装置由雨鸟LF1200型喷头(喷嘴直径2.18 mm，喷射仰角17°，工作压力范围170～410 kPa)、视频雨滴谱仪(Two-dimensional video disdrometer,2DVD)、压力传感器(西安新敏CYB型，量程0～500 kPa，精度0.1%)、变频恒压供水节能控制柜、加压泵、不锈钢水箱、PVC管、阀门以及其它必需的试验设备等组成，如图1所示。

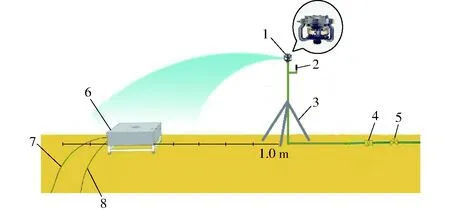
图1 试验装置示意图Fig.1 Diagram of experimental setup1.喷头 2.压力传感器 3.喷头支架 4.流量计 5.压力调节阀 6.视频雨滴谱仪 7.电源线 8.数据线

1.2 试验方法

虽然喷头工作压力是影响喷洒水滴直径的重要因素之一，但是在实际喷灌工程建设时，为了保证喷灌系统灌溉质量，喷头设计工作压力一般采用喷头额定工作压力(通常由厂家给出)。由于本文重点研究地形坡度对喷洒水滴直径和动能强度分布的影响，所以喷头工作压力采用厂家推荐值300 kPa。地形坡度设置3个水平，分别是0、0.1和0.2，为了下文叙述方便，用坡度的正值表示下坡，负值表示上坡，0表示平坡，即：平坡、坡度为0.1的上坡和下坡、坡度为0.2的上坡和下坡，分别用0、-0.1、0.1、-0.2和0.2表示。由于在室内通过人为手段模拟坡面，并把视频雨滴谱仪(质量达80 kg)直接放到坡面上来获取水滴信息十分困难，所以试验过程中通过改变喷头安装高度和视频雨滴谱仪位置来调节两者之间的相对高差和水平距离，模拟视频雨滴谱仪在坡面上不同的位置，进而测试坡面上不同位置处的喷灌水滴直径和速度。从距离喷头1 m处到喷洒水流射程范围内，以1 m间距(坡面距离)测定各个位置上的水滴直径和速度，并控制每个测点收集不少于10 000个水滴[19]。

喷洒范围内即使是同一位置处，其水滴直径变化范围也较大，通常采用平均水滴直径来表示不同位置处的水滴大小。常用的计算水滴直径的方法有：个数加权平均法、体积加权平均法和中数直径法。有学者对这3 种方法进行了对比分析，发现体积加权平均法计算的水滴直径沿射程变化规律能更好地符合实际[20]，其计算公式为

(1)

dm——测试点测得水滴对应的水滴直径，mm

n——测试点测得的水滴个数

通过2DVD可直接测得单个水滴的垂直速度vt以及在水平方向上相互垂直的2个水平速度vh1和vh2，则水滴的合速度v计算公式为

(2)

2 结果与分析

2.1 不同坡度下水滴直径沿射程分布

图2给出了不同坡度下水滴平均直径沿射程分布情况。从图中可以看出，不同坡度下水滴平均直径随着与喷头距离的增大而增大，并且在射程末端达到最大。但是与喷头距离小于6 m时，不同坡度下水滴平均直径的差异较小；当与喷头距离大于6 m时，不同坡度下水滴平均直径的差异变大。在与喷头相同距离时，水滴平均直径随着坡度增大而减小。

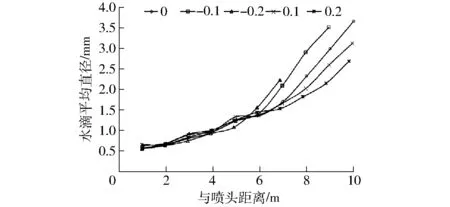
图2 不同坡度下水滴平均直径沿射程分布Fig.2 Distribution of average droplet diameter along spray direction under different slopes

表1 不同坡度下水滴平均直径与与喷头距离的指数关系式及R2Tab.1 Exponential relationships between average droplet diameter and distance from sprinkler under different slopes and their R2 values

从表1可以看出，系数a随着坡度的减小而减小，系数b随着坡度的减小而增大，系数a和b与坡度i呈较好的线性关系

a=0.29i+0.43 (R2=0.88)

(3)

b=0.21-0.19i(R2=0.95)

(4)

(5)

平均直径只能从宏观上反映水滴直径沿射程的变化关系，为了进一步分析水滴直径分布规律，图3给出了不同坡度下水滴直径沿射程频率分布情况。从图中可以看出，当与喷头坡面距离为1 m时，不同坡度下水滴直径的分布极为相似，主要以小直径为主，直径小于0.5 mm的水滴个数均占到90%以上，说明喷头附近的水滴直径分布与坡度关系不明显，仅与喷头本身的性能有关。当与喷头坡面距离增加到3 m时，不同坡度下水滴直径分布开始发生变化，小直径水滴数量减少，大直径水滴数量增多。在平地上喷洒时，水滴直径基本在0～1.0 mm范围内，其中小于0.5 mm和0.5～1.0 mm水滴数量相当，对应的水滴频率均为46%。在坡地上喷洒时，在上坡方向，小于0.5 mm水滴数量大于0.5～1.0 mm水滴数量，且随着坡度的逐渐增大，小于0.5 mm水滴数量不断增多，0.5～1.0 mm水滴数量不断减少。而下坡方向的情况恰好相反，这与与喷头的绝对距离有关，与喷头的绝对距离越小，小水滴数量越多。随着与喷头坡面距离的继续增加，水滴直径分布范围继续扩大，当与喷头坡面距离为5 m时，水滴直径范围扩大至2.0 mm，不同坡度下水滴直径分布均大致呈“正态分布”趋势，即中间高，两边低，其中0.5～1.0 mm的水滴所占比例最大，不同坡度下该范围的水滴频率均达到50%以上，且小于0.5 mm的水滴数量大于1.0～1.5 mm的水滴数量。当与喷头坡面距离进一步增大到7 m时，水滴直径分布范围扩大至2.5 mm，未达到射程末端的其余不同坡度下的水滴直径分布虽然仍呈“正态分布”趋势，但其峰值减小，呈压扁态势。当与喷头坡面距离增加到射流末端时，水滴直径分布范围达到最大，为3.5 mm，小水滴(小于0.5 mm)数量急剧增多，大水滴数量急剧减少，但不同坡度下最大水滴直径都出现在射程末端。

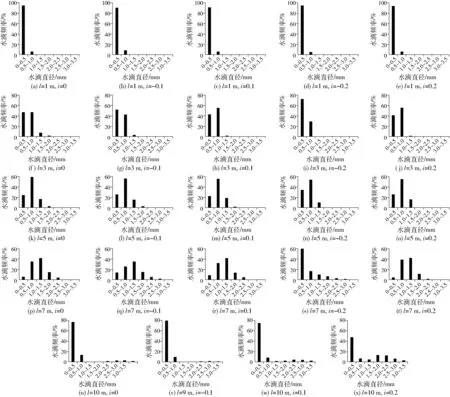
图3 不同坡度下水滴直径沿射程频率分布Fig.3 Frequency distributions of droplet diameter along spray direction under different slopes

图4 不同坡度下水滴速度与直径的关系Fig.4 Relationships between droplet velocity and diameter under different slopes

2.2 不同坡度下水滴速度与直径的关系

速度是水滴信息中的重要参数，是衡量水滴打击动能的关键指标。图4给出了不同坡度下沿射程不同位置处喷洒水滴速度与直径的关系。从图中可以直观地看出，水滴速度与直径的关系可以分为2个阶段，第1阶段，当水滴直径小于0.5 mm时，水滴速度随着直径的增大呈减小趋势；第2阶段，当水滴直径大于0.5 mm时，水滴速度随着直径的增大呈增大趋势。但是，由于不同坡度下，直径小于0.5 mm且速度大于4 m/s的水滴个数与直径小于0.5 mm所有水滴个数比例均不到3%，水滴速度与直径在第1阶段的关系不占主要地位，这种关系可以忽略。因此，总体而言，不同坡度下水滴速度均随水滴直径的增大呈增大趋势，且符合对数函数关系，可用公式v=plnd+q来表示，其中d为水滴直径，mm；p和q均为相应系数。

表2给出了不同坡度下水滴速度与水滴直径的对数关系式及R2。从表2中可以看出，系数p和q均随着坡度的增大而增大，并呈较好的线性关系，且决定系数均不小于0.95，通过统计回归分析得出系数p和q分别与坡度i的关系式为

p=1.01i+1.65 (R2=0.99)

(6)

q=0.84i+3.58 (R2=0.95)

(7)

将式(6)、(7)代入v=plnd+q中，可以得出水滴速度v与直径d及坡度i的关系式为

v=(1.01i+1.65)lnd+0.84i+3.58

(8)

表2 不同坡度下水滴速度与直径的对数函数关系式及R2Tab.2 Logarithmic relationships between droplet velocity and diameterunder different slopes and their R2 values

2.3 不同坡度下喷洒水滴动能强度分布

2.3.1动能强度计算

动能强度是指单位时间内测点处的动能，它是反映喷灌系统降水能量分布、预测地表径流的重要参数，其值取决于喷洒水滴的直径、速度和喷灌强度，计算式[19]为

(9)

式中Wj——与喷头不同距离测点处的打击动能强度，W/m2

vm——第m个水滴速度，m/s

ρ——水的密度，kg/m3

j——与喷头不同距离的测点

2.3.2动能强度模拟值与实测值的对比分析

利用各测点处实测的水滴直径和速度及喷灌强度数据，通过式(9)可获得各测点处喷洒水滴动能强度的实测值。另外，已知地形坡度和测点位置，通过本文提出的水滴平均直径与至喷头距离的关系式(5)，可计算出测点处的水滴平均直径，将水滴平均直径代入本文提出的水滴速度与直径的关系式(8)，可计算出水滴平均直径相对应的速度，然后应用文献[21]中提出的坡地喷灌水量分布计算模型，计算出该测点处的喷灌强度，最后把测点处水滴平均直径、速度和喷灌强度的计算值代入式(9)，便可模拟出测点处喷洒水滴动能强度。

图5为喷头工作压力为300 kPa、坡度为0.2和-0.2时模拟的动能强度沿射程分布与实测情况的对照图，以验证喷洒水滴动能强度模拟方法的正确性。从图中可以看出，大部分动能强度模拟值与实测值比较接近，相对偏差在10%以内，而有少部分模拟值与实测值偏差较大，超过15%，最大达到28%，这主要是因为这些测点处的喷洒水滴平均直径、速度或者喷灌强度的计算值与实测值出现较大偏差，但是总体而言，喷洒水滴动能强度模拟结果在一定程度上能够比较准确地反映动能强度分布规律。

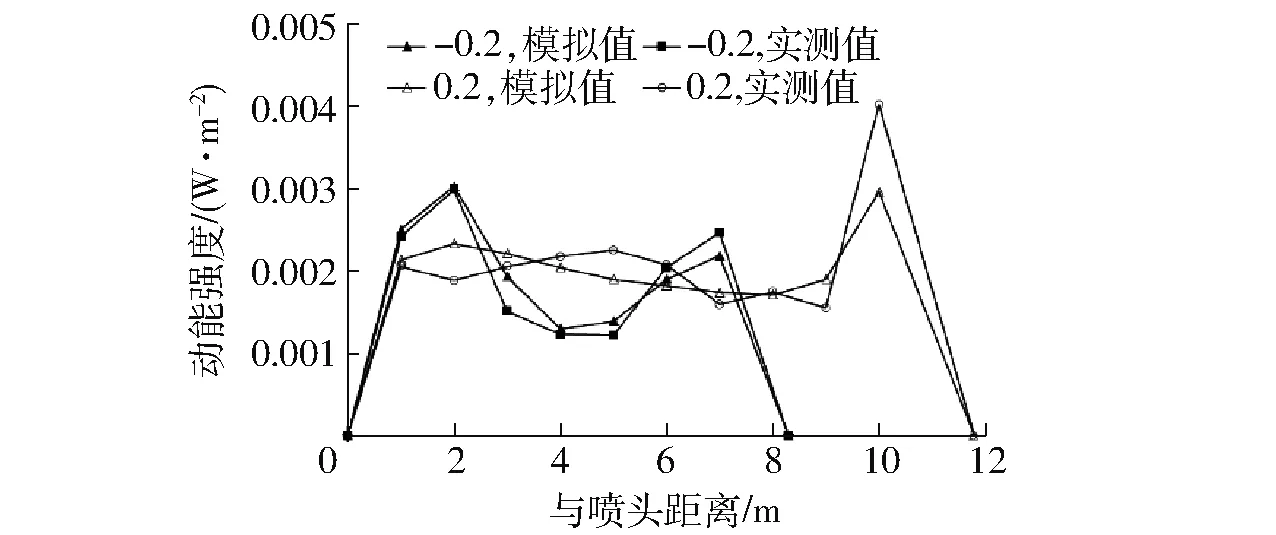
图5 动能强度沿射程分布的模拟值与实测值对比Fig.5 Comparison of measured and simulated kinetic energy intensity distribution along spray direction

2.3.3单喷头坡面动能强度分布

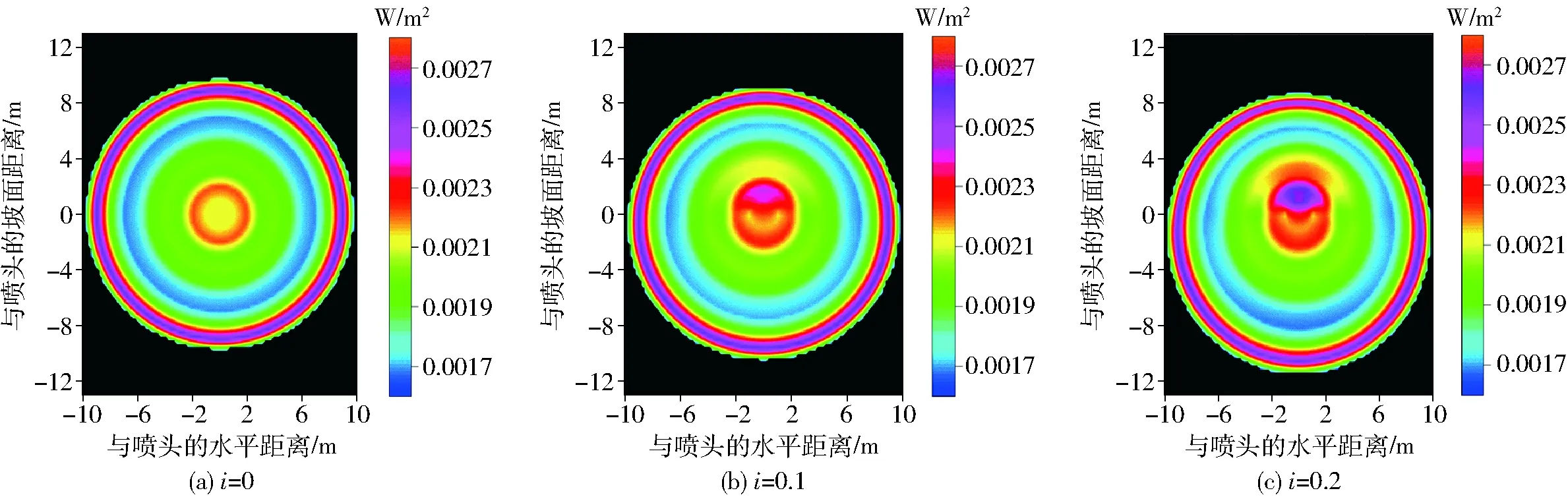
图6 不同坡度下单喷头喷洒水滴坡面动能强度分布Fig.6 Kinetic energy distributions for single sprinkler under different slopes

利用上述喷洒水滴动能强度模拟方法，计算出不同坡度下单喷头坡面动能强度分布情况，如图6所示。坐标点(0,0)为喷头位置。从图中可以看出，不同坡度下，动能强度高值区主要分布在喷头附近和射程末端，且随着坡度的增大，高值区在喷头附近的范围有所扩大。上坡方向，与喷头相同位置处的动能强度随坡度增加而增大，这主要是因为坡度增加，上坡射程减小，喷洒湿润区随之减小，导致喷灌水量不断向上坡集中，所以与喷头相同位置处喷灌强度也随之变大。下坡方向，由于下坡射程随着坡度增加而增大，喷洒湿润区不断扩大，致使喷灌水量在下坡方向分布变稀薄，与喷头相同位置处喷灌强度也随坡度增大而变小，所以导致其动能强度也因此减小。

积极构建以政治改造为统领的五大改造新格局，科学引领监狱发展新实践，把提高政治站位，坚守安全底线，践行改造宗旨的“总目标”与“五大改造”新格局的“路线图”，作为推进新时代监狱工作根本遵循，确保监狱改造工作取得新成效。

2.3.4组合喷头坡面动能强度分布

一个喷灌系统由很多喷头组合而成，仅研究单喷头坡面动能强度分布对工程实践意义不大。因此，利用本文的喷洒水滴动能强度模拟方法，先计算出单喷头动能强度分布，然后再按照不同喷头布置方式和间距对单喷头数据进行叠加，进而获得组合喷头坡面动能强度分布规律，以期为坡地喷灌系统设计提供一定的科学依据。

(1)喷头布置方式对坡面动能强度分布的影响

图7给出了坡度为0.1、喷头间距为10 m(平地喷头射程R)的正方形和三角形2种布置方式组合喷头坡面动能强度分布情况。在正方形布置下，4个喷头分别位于正方形4个顶点，如图7a所示，其动能强度分布呈十字花形，方形中部和4个角为动能强

度高值区，其各点动能强度均大于0.006 W/m2，高值区(大于0.006 W/m2)占整个喷洒区域的比例为52.9%，且上方2个喷头之间均存在1个动能强度低值区，其值都在0.004 W/m2左右。在三角形布置下，3个喷头分别位于三角形3个顶点，如图7b所示，高值区主要位于3个喷头附近，其面积占整个喷洒区域的比例为40%，而其他区域各点动能强度均在0.005 W/m2左右。三角形布置下的动能强度分布比正方形布置的更为均匀，其动能强度分布均匀系数[14]分别为90.8%和77.8%。因此，三角形布置对于减小喷头打击动能强度具有一定作用，坡地喷灌系统设计时，在满足喷灌均匀性前提条件下，喷头布置建议优先考虑三角形布置方式。

(2)喷头间距对坡面动能强度分布的影响

图8给出了坡度为0.1、三角形布置方式下不同喷头间距对组合坡面喷头动能强度分布的影响。

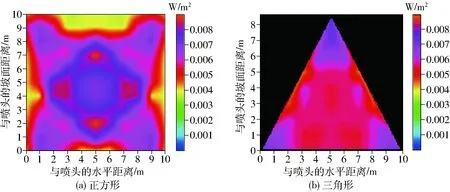
图7 不同喷头布置方式下组合喷头喷洒水滴坡面动能强度分布Fig.7 Kinetic energy intensity distributions for combined sprinklers with different sprinkler layouts

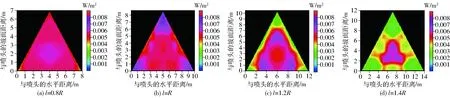
图8 不同喷头间距下组合喷头喷洒水滴坡面动能强度分布Fig.8 Kinetic energy intensity distributions for combined sprinklers with different sprinkler spacings

从图中可以看出，随着喷头间距的增大，动能强度分布越来越不均匀，4种间距(0.8R、R、1.2R和1.4R)下动能强度分布均匀系数分别为94.9%、90.8%、74.2%和68.5%。当喷头间距为0.8R时，其动能强度基本在0.005～0.006 W/m2之间。喷头间距增大至R时，出现高值区，主要位于3个喷头附近；随着喷头间距进一步增大，高值区占整个喷洒区域的比例不断减小，喷头间距为R、1.2R和1.4R下高值区所占比例分别为40.0%、28.6%和10.8%，且高值区逐步向三角形区域的中心部位移动。过高的动能强度将对土壤表面带来破坏，因此，从喷洒水滴打击动能角度考虑，对于雨鸟LF1200型喷头在坡地应用时选择0.8R的间距比较适宜，这与文献[21]从水量分布研究结果选取的喷头间距相吻合。

(3)坡度对坡面动能强度分布的影响

图9给出了喷头间距为1.2R、三角形布置方式下不同坡度对组合喷头坡面动能强度分布的影响。从图中可以看出，随着坡度增大，动能强度高值区由喷洒区域中心部位逐渐移向底部，这与不同坡度下单喷头水量分布发生较大变化有关。3种坡度下(0、0.1和0.2)，其动能强度高值区所占比例分别为27.1%、28.6%和28.6%，动能强度分布均匀系数分别为74.3%、74.2%和73.4%，由此说明坡度变化对组合喷头动能强度分布影响不明显。

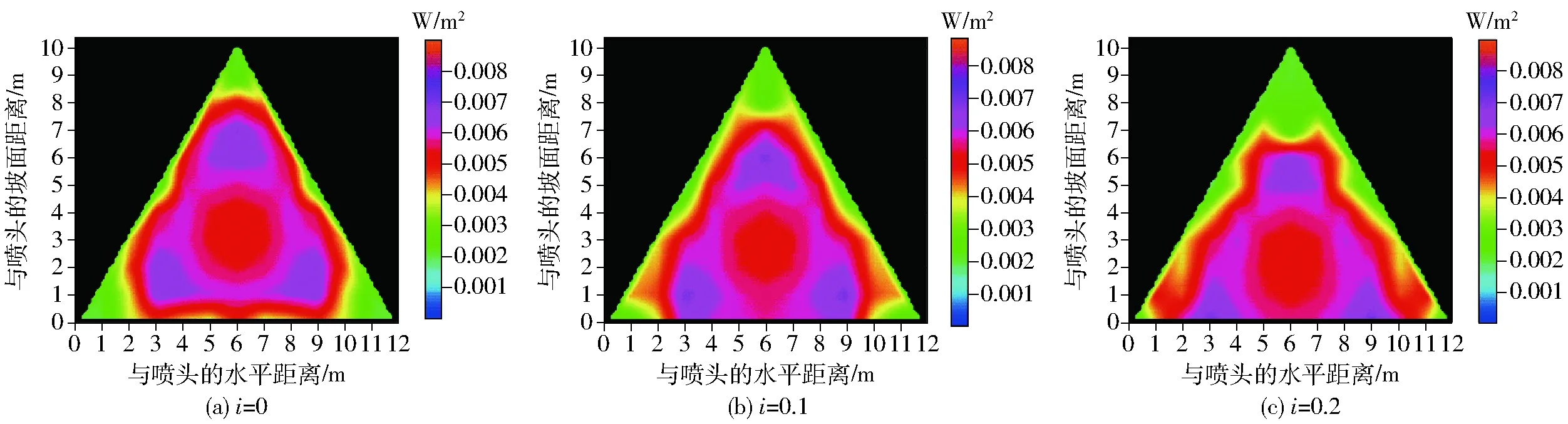
图9 不同坡地下组合喷头喷洒水滴坡面动能强度分布Fig.9 Kinetic energy intensity distributions for combined sprinklers under different slopes

3 结论

(1)在室内无风条件下，利用视频雨滴谱仪实时监测了不同坡度下喷洒水滴直径和速度等信息，揭示了不同坡度下水滴平均直径及直径频率沿射程方向的变化规律，分别建立了平均直径、速度与坡度等因素之间的数学关系。水滴平均直径与喷头距离呈较好的指数函数关系，水滴速度与直径呈较好的对数函数关系。

(2)以水滴平均直径、速度与坡度等之间的数学关系为基础，结合以往的坡地喷灌水量分布计算方法，提出了无风条件下坡地喷洒水滴动能强度计算模型。将模拟的动能强度与实测值进行对照，结果表明，大部分动能强度模拟值与实测值比较接近，相对偏差在10%以内。总体而言，模拟结果在一定程度上能够比较准确反映喷洒水滴动能强度分布规律。

(3)以雨鸟LF1200型喷头为对象，应用模型，分别研究了单喷头和组合喷头2种情况下的坡面动能强度分布规律。对于单喷头而言，不同坡度下动能强度高值区主要分布在喷头附近和射程末端，且随着坡度的增大，高值区在喷头附近的范围有所扩大。在上坡方向，至喷头相同位置处，坡度越大，其动能强度越大，在下坡方向，结果反之。对于组合喷头而言，随着喷头间距的增大，动能强度分布越来越不均匀，且动能强度高值区所占比例不断减小，坡度变化对坡面动能强度分布影响并不明显，而三角形布置方式对于减小坡地喷灌打击动能强度具有一定作用。

(4)同时考虑打击动能强度和水量分布，在坡地喷灌系统设计时若选用雨鸟LF1200型喷头，建议优先采用三角形布置，且间距为0.8R(R为平地喷头射程)。

1 李久生. 喷洒水滴分布规律的研究[J]. 水利学报, 1988,19(10): 38-45.

2 金兆森, 蒋定生, 田虎旗, 等. 喷洒水滴大小对土壤结构及作物的影响[J]. 节水灌溉, 1981(2): 31-35.

3 徐红, 龚时宏, 贾瑞卿, 等. 新型ZY系列摇臂旋转式喷头水滴直径分布规律的试验研究[J]. 水利学报, 2010, 41(12): 1416-1422.

XU Hong, GONG Shihong, JIA Ruiqing, et al. Study on droplet size distribution of ZY sprinkler head[J]. Journal of Hydraulic Engineering, 2010, 41(12): 1416-1422. (in Chinese)

4 白更, 严海军, 王敏. 喷洒水滴直径面粉测定法改进[J]. 农业机械学报, 2011, 42(4): 76-80.

BAI Geng, YAN Haijun, WANG Min. Measuring sprinkler droplet size with modified flour methodology[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(4):76-80. (in Chinese)

5 李红, 任志远, 汤跃, 等. 喷头喷洒雨滴粒径测试的改进研究[J]. 农业机械学报, 2005, 36(10): 50-53．

LI Hong, REN Zhiyuan, TANG Yue, et al. Measurement and amelioration of the test to raindrop size of sprinklers[J]. Transactions of the Chinese Society for Agricultural Machinery, 2005, 36(10): 50-53. (in Chinese)

6 韩文霆, 曹培, 刘文帅. 人工模拟降雨系统喷头喷洒雨滴特性测试[J/OL]. 农业机械学报, 2014, 45(12): 56-61. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20141209&journal_id=jcsam. DOI: 10.6041/j.issn.1000-1298.2014.12.009.

HAN Wenting, CAO Pei, LIU Wenshuai. Raindrop characteristics of sprinklers for artificial rainfall system[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(12): 56-61. (in Chinese)

7 MONTER J, TARJUELO J M, CARRIN P. Sprinkler droplet size distribution measured with an optical spectropluviometer[J]. Irrigation Science, 2003,22(2): 47-56．

8 严海军, 肖建伟, 李文颖, 等. 圆形喷灌机低压阻尼喷头水滴直径分布规律的试验研究[J]. 水利学报, 2014, 45(4): 467-473.

YAN Haijun, XIAO Jianwei, LI Wenying, et al. Droplet size distributions of low-pressure damping sprinklers used in center-pivot irrigation systems[J].Journal of Hydraulic Engineering, 2014, 45(4): 467-473. (in Chinese)

9 刘俊萍, 刘兴发, 朱兴业, 等. 摇臂式喷头与全射流喷头水滴分布对比试验[J]. 农业工程学报, 2015, 31(18): 85-91.

LIU Junping, LIU Xingfa, ZHU Xingye, et al. Comparison of droplet size distribution experiments between complete fluidic sprinkler and impact sprinkler[J]. Transactions of the CSAE, 2015, 31(18): 85-91. (in Chinese)

10 SALVADOR R, BAUTISTA-CAPETILLO C, BURGUETE J, et al. A photographic method for drop characterization in agricultural sprinklers[J]. Irrigation Science, 2009, 27(4): 307-317.

11 BAUTISTA C, ROBLES H, SALINAS E, et al. A particle tracking velocimetry technique for drop characterization in agricultural sprinklers[J]. Irrigation Science, 2014, 41(4): 602-607.

12 MCCREERY G E, STOOTS C M. Drop formation mechanism and size distributions for spray plate nozzles[J]. International Journal of Multiphase Flow, 1996, 22(3): 431-452.

13 朱兴业, 刘兴发, 刘俊萍, 等. 基于LPM的摇臂式喷头水滴分布试验研究[J]. 排灌机械工程学报, 2015, 33(10): 908-914.

ZHU Xingye, LIU Xingfa, LIU Junping, et al. Droplets distribution research of impact sprinkler based on laser precipitation monitor[J]. Journal of Drainage and Irrigation Machinery Engineering, 2015, 33(10): 908-914. (in Chinese)

14 朱兴业, 刘兴发, 刘俊萍, 等. 全射流喷头喷洒水滴动能分布规律[J]. 农业工程学报, 2015, 31(15): 26-31.

ZHU Xingye, LIU Xingfa, LIU Junping, et al. Droplet kinetic energy distribution regulation of complete fluidic sprinkler[J].Transactions of the CSAE, 2015, 31(15): 26-31. (in Chinese)

15 MOHAMMED D, KOHL R A. Infiltration response to kinetic energy[J]. Transactions of the ASAE, 1987, 30(1): 108-111.

16 李久生, 马福才. 喷嘴形状对喷洒水滴动能的影响[J]. 灌溉排水, 1997, 16(2): 1-6.

LI Jiusheng, MA Fucai. Effect of nozzle shape on the spray drop kinetic energy from sprinklers[J]. Journal of Irrigation and Drainage, 1997, 16(2): 1-6. (in Chinese)

17 BUBENZER G D, JONES B A. Drop size and impact velocity effects on the detachment of soils under simulated rainfall[J]. Transactions of the ASAE, 1971, 14(4): 851-864.

18 THOMPSON A L, REGMI T P, GHIDEY F, et al. Influence of kinetic energy on infiltration and erosion[C]∥Soil Erosion Research for the 21st Century, Proceedings of the International Symposium, 2001: 151-154.

19 巩兴晖, 朱德兰, 张林, 等. 基于 2DVD 的非旋转折射式喷头水滴直径分布规律[J/OL].农业机械学报, 2014, 45(8): 128-133. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20140821&journal_id=jcsam. DOI: 10.6041/j.issn.1000-1298.2014.08.021.

GONG Xinghui, ZHU Delan, ZHANG Lin, et al. Drop size distribution of fixed spray-plate sprinklers with two-dimensional video disdrometer[J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(8): 128-133. (in Chinese)

20 李久生. 谈平均水滴直径的计算方法[J]. 喷灌技术, 1987(4): 21-23.

21 张以升, 张林, 朱德兰,等. 基于弹道理论坡地喷灌水量分布模拟及均匀度计算[J]. 农业工程学报, 2016, 32(13): 59-66.

ZHANG Yisheng, ZHANG Lin, ZHU Delan, et al. Simulation of water distribution and calculation on water application uniformity for sprinkler irrigation on sloping land based on ballistic theory[J]. Transactions of the CSAE, 2016, 32(13): 59-66. (in Chinese)