林区步行最优路径分析方法

陈玥璐 赵天忠 武 刚 陈飞翔

(北京林业大学信息学院， 北京 100083)

0 引言

步行(Walking)是人们在林区实施森林调查、培育和经营作业，执行抢险、救援任务，开展科学研究和进行休闲游憩活动的重要交通方式。步行最优路径分析是以GIS数据建立步行环境模型，利用优化算法计算满足特定目标的最优路径。探索林区复杂环境下的步行最优路径分析方法、辅助和支持寻路(Way-finding)决策、提升寻路效率，具有研究价值和应用意义。

然而，已有研究主要是以矢量路网建模步行环境，考虑路径长度[1]、步行时间[2]、耗氧量[3]、地标数量[4]、路径复杂度[5]、主观判断时间[6]等因素，利用图论算法[1]或仿生学算法[7]计算单目标或多目标约束的最优路径，无法适用于林区开放的步行环境。栅格路径分析以栅格成本表面表示连续的开放空间，建立栅格单元间的拓扑关系，构造栅格网络模型，进而计算最优路径[8]，能够有效解决开放空间中的寻路问题[9-10]。有学者以最短步行时间[11-12]或最小、最大可视性[13-14]为目标计算最优路径，但单一目标约束的路径无法满足多目标的路径需求[15]。还有学者综合考虑地形、地类、植被、土壤、雨洪安全、地质灾害、文化遗产与生物保护[16-18]等因素进行路径分析，但此类研究均是基于现有GIS软件，采用不同的方法和步骤，针对特定林区路径优化问题(公路或步道规划设计)的应用，缺少一个统一的方法解决林区步行最优路径的分析问题。另外，尽管林区步行环境主要为大尺度开放空间(Open space)，但道路网络(Road network)仍是行人重要的寻路参考，现有的栅格路径分析仅计算单一的越野路径(Off-road path)，未考虑到已有道路信息，影响了路径分析结果的有效性和可靠性。

针对林区步行寻路活动的特殊性，本文设计统一的林区步行最优路径分析方法(Optimal walking path analysis method for forest region，OWPAM-FR)，将特定的林区步行寻路问题抽象为一般的通用性问题，根据输入的数据和参数，利用模式化的步骤建立面向不同寻路需求的栅格网络模型，以便引入优化算法进行路径分析。

1 OWPAM-FR原理

林区步行寻路活动具有特殊性：客观上，步行环境是融合了离散道路网络与连续开放空间的混合空间(Hybrid space)。行人既能沿道路行走，也可越野行走。主观上，行人往往具有不同的林区活动类型，同时权衡自然环境、个体能力等因素，存在多样化的寻路目标。如救援人员倾向于选择时间较短的路线同时不至于难度过大，登山者希望沿安全的道路行走同时不容易迷路。因此，林区步行最优路径分析应满足如下原则：应能充分考虑林区步行环境的复杂性，对混合空间进行建模，同时使路径结果顾及多个寻路目标并偏重于不同的主要目标，具有良好的适用性。

可步行性(Walkability)是步行空间的重要评价指标，被广泛应用于城市规划、建筑设计等领域[19]。本文引入了可步行性的概念，将不同环境因素影响下的林区地形表面定性划分为不可行域、可行域和易行域。相关概念如下：

(1)可步行性：林区环境因素影响下，地形表面对步行活动的友好程度。

(2)不可行域(Unwalkable area)：可步行性较差，行人无法步行通过的区域。不可行域可分为绝对不可行域和相对不可行域。绝对不可行域一般是阻碍步行的地理实体，如沟壑、湖泊、围墙、建筑物。相对不可行域是满足特定条件时无法步行通过的区域。如坡度大于40°或植被盖度高于90%的区域。

(3)可行域(Walkable area)：可步行性适中，行人能够步行通过但需要考虑步行成本的区域。步行成本可按来源分为地形成本与地物成本两类，地形成本一般包括距离、坡度、步行时间、体能消耗等，地物成本分为覆盖物成本和地标可视成本。

(4)易行域(Easy-to-walk area)：可步行性良好，行人能够步行通过并可降低步行成本的区域。易行域一般是道路网络覆盖的区域，如公路、步道、小径，能够有效降低地物成本。如公路可以忽略植被覆盖的影响，同时避免行人迷路。

步行活动的本质是行人在与环境交互的基础上进行的避障行为[20]，不同类型的行人在这一层面上具有相似性。通过定义上述概念，可将林区步行最优路径分析问题抽象为避让不可行域，在可行域与易行域中计算多目标最小成本路径的问题。OWPAM-FR以此为理论基础，首先利用综合可步行性栅格(Comprehensive walkability raster，CWR)表示由不可行域、可行域和易行域构成地形表面的可步行性特征；随后针对每个栅格单元，利用方向模型建立其与相邻栅格间的邻接关系，引入步行成本计算方法计算可行域和易行域中邻接栅格单元间的步行成本；最后建立由有向加权图表示的栅格网络模型，引入经典最短路径算法求解最优步行路径。基于CWR建立栅格邻接关系能够通过判断条件排除不可行域，并在计算步行成本时考虑易行域对某些成本的削减效应，有效建模混合空间。同时，在步行成本计算时进行分类，根据不同的寻路需求选取特定的步行成本，并引入统一目标法将多个成本组合为一个综合步行成本，实现顾及多个目标同时偏重主要寻路目标的路径优化。模式化的步骤便于考虑多样化的类型林区步行活动，顾及不同的寻路目标，具有一定的适用性。

2 OWPAM-FR设计

2.1 综合可步行性栅格

2.1.1相关定义

综合可步行性栅格是顾及环境因素的影响，定性描述地形表面可步行特征的栅格集合，在本文中以A表示。

A={Aij|1≤i≤X,1≤j≤Y}

(1)

式中X、Y——A中栅格单元的行数和列数

Aij——A中第i行、j列的栅格单元

根据行人对环境因素影响下栅格单元的可步行性定性评价，以u(i,j)表示Aij存储的数值，则Aij的可步行性描述为

(2)

由具有相同可步行性的栅格单元构成的集合即为不可行域、可行域和易行域，分别以U、W、E表示，为

U={Aij|Aij∈A,u(i,j)=-1}

(3)

W={Aij|Aij∈A,u(i,j)=1}

(4)

E={Aij|Aij∈A,u(i,j)=0}

(5)

2.1.2构建方法

地图代数是栅格空间分析的核心和重要工具[21]，CWR的构建是基于地图代数的栅格叠置分析过程。本方法将多源异构GIS专题数据表达的步行环境信息转化为统一的栅格数据结构，在相同的分析环境下进行多图层的局部运算。基本原理是：首先将地形表面默认为可行域；随后提取单一环境因素影响下的不可行域，构建单因素不可行栅格，并组合为综合不可行栅格；最后，与易行栅格叠加得到综合可步行性栅格。如图1所示，具体步骤如下：

(1)构建绝对不可行栅格。将矢量的不可行要素转换为栅格数据表示的不可行域，不可行栅格单元的值为0，其余为1。

(2)相对不可行栅格构建。对于矢量的连续数据，需要先将其转换为栅格表面。引入不可行阈值对栅格表面进行重分类，构造相对不可行域。不可行栅格单元的值为0，其余为1。

(3)综合不可行栅格构建。对多个单因素不可行栅格执行布尔交运算(And)，并对运算结果执行新值替代操作，以-1替代0。

(4)易行栅格构建。与步骤(1)类似地将矢量的易行要素转换为栅格数据表示的易行域，易行栅格单元的值为0，其余为1。

(5)综合可步行性栅格构建。对综合不可行栅格与易行栅格执行算术乘法运算，得到CWR。

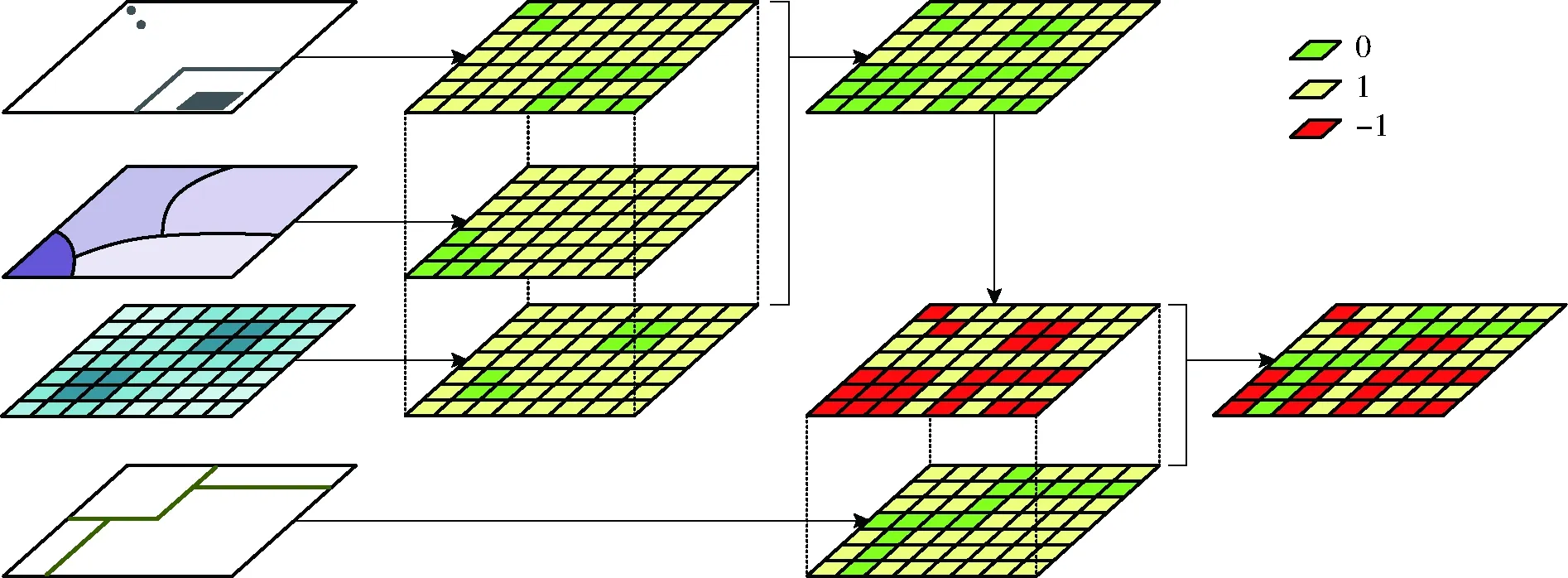
图1 综合可步行性栅格的构建过程Fig.1 Building process of CWR

CWR应能达到一定精度，反映足够丰富的环境细节。然而，栅格单元越小，所建立的栅格网络数据量越大，导致路径优化算法占用内存空间较大、计算效率较低[22-23]。因此，栅格尺寸应在满足分析需求的同时足够大，以节省存储空间并提高计算效率，一般与输入的格网DEM相同即可。

2.2 步行成本计算

本方法基于CWR构建栅格单元间的邻接关系，计算步行成本。邻接关系的建立一般可采用4、8、24方向邻域模式[24]。基于4方向邻域栅格网络计算得到的路径呈锯齿状，而24方向邻域栅格网络计算得到的路径单元可能在地理上不相邻[10]，均存在一定误差。因此，本文采用8方向邻域模式，只考虑中心栅格单元与其周围八方向相邻栅格单元间的邻接关系。按顺序对CWR中的栅格单元进行编号，以c表示邻域的中心栅格单元号，a表示c的相邻栅格单元号，c、a可由栅格单元位于CWR的行列号i、j计算得到。如图2所示，以O(c,a)表示a相对于c的邻域编号。

图2 8方向邻域模式Fig.2 Queen’s pattern

如上文所述，步行成本分为地形成本和地物成本。地形成本一般包括坡度、平面与空间距离，地物成本则分为覆盖物成本和地标可视成本。步行时间和体能消耗是重要的寻路目标，但容易受到个体和环境等多方面因素影响，通常难以精确的量化，现有研究只考虑地形因素产生的时间和能耗成本。本文同样基于地形因素计算时间和能耗，将其余环境因素归为地物成本。

单一目标约束的路径无法满足行人的路径需求[15]，林区步行路径分析需要顾及多个寻路目标同时偏重于主要目标，实质上是一个多目标优化问题。利用统一目标法将多目标问题转化为单目标问题，即可直接引入成熟的路径分析方法进行求解。首先，根据需要计算路径的单因素成本。随后，采用加权组合法将多个单因素成本按一定的权重组合为综合步行成本，权重的分配能够体现不同类型行人对路径成本的重视程度。将综合步行成本作为栅格网络中的边的权值，引入最短路径算法，即可实现林区步行最优路径的求解。

2.2.1地形成本计算

(1)坡度与距离

坡度和距离是基于网格DEM计算得到的基本地形成本，计算式为

(6)

(7)

(8)

式中S——从栅格单元c到a对应不同邻域O(c,a)的坡度成本

Dh——从栅格单元c到a对应不同邻域O(c,a)的平面距离成本，m

Ds——从栅格单元c到a对应不同邻域O(c,a)的空间距离成本，m

x、y——栅格单元在水平和竖直方向上的长度，m

zc、za——栅格单元c、a的高程，m

对于一般的方形规则格网DEM，邻域O(c,a)为2和7与O(c,a)为4和5对应的计算式相同。

(2)步行时间

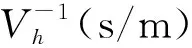
(9)

则从栅格单元c到a的步行时间成本为

(10)

(3)体能消耗

体能消耗成本是人类步行活动所消耗的能量，也可由热量或耗氧量间接表示。体能消耗的量算一般是以坡度作为变量基于运动生理学实验建立预测模型，但往往具有范围限制。为便于计算，本文以单位体重能耗(J/kg)表示体能消耗成本，引入改进的Minetti步行能量消耗预测公式[15,26]，计算从栅格c到a单位体重距离能耗J(J/(kg·m))，能够适用于更大的坡度范围。J与坡度S的关系为

(11)

则从栅格单元c到a的体能消耗成本Q为

Q=DsJ

(12)

2.2.2地物成本计算

(1)覆盖物成本

本文将地形表面的地物覆盖造成的通行成本视为一类覆盖物成本，引入覆盖物栅格(Land cover raster，LCR)进行计算。LCR作为成本表面模型，储存行人通过每个栅格单元的成本或困难程度。覆盖物成本一般为2个相邻栅格单元覆盖物成本的均值，对于可由易行域消除的覆盖物成本，引入综合可步行性栅格参与计算。计算公式为

(13)

式中L——由栅格单元c步行到a花费的覆盖物成本

lc、la——LCR中栅格单元c、a的值

uc、ua——CWR中栅格单元c、a的值

(2)地标可视成本

陌生的环境会对行人造成认知负荷[1,4,5,7]。林区中的地标能够有效辅助人们对环境的感知和记忆，降低人们的认知负荷并提高寻路效率，是重要的寻路要素[27-29]。可视是地标发挥导航作用的必要条件，已有学者以可视信息作为通行成本进行路径规划[5,13,14,30]。因此，将地标可视性引入路径分析，实现林区路径的地标可视最优化具有一定的现实意义。本文引入地标可视成本，将其定义为路径上的人观察地标的困难程度。不同于一般的可视性分析问题，林区地标容易受到地物遮挡，其可视特征具有不确定性，难以用二值地形可视性描述，利用概率描述地标相对某一视点的模糊可视性更加合理。本文将地标可视成本定义为行人位于当前位置无法看到地标的概率(地标不可视概率)，利用地标不可视概率栅格(Landmark invisible probability raster，LIPR)进行表示。栅格单元c处的地标可视成本为

(14)

式中m——LIPR中栅格单元c视线范围内的地标数量

pm——第m个地标相对单元c的可视概率

易行域能够引导行人的步行行为，可作为地标提供寻路参考。因此，从栅格c到a的地标可视成本为

(15)

式中ga——栅格单元a处的地标可视成本,可由式(14)计算得到

由于林区视线受距离、地类、树种、季节、气候、时间、日照等因素影响，精确量算地标的可视概率是一个复杂的可视性分析问题。由于林下行人的视线主要受到地形和树冠的遮挡，本文将传统地形二值可视性与所在栅格单元郁闭度的乘积作为pm构建LIPR。

2.2.3综合步行成本计算

综合步行成本是多个单因素成本的加权组合，成本的权重分配能够体现不同寻路目标对行人的重要程度。首先采用极大值标准化法，消除栅格c到a的第n个单因素步行成本的量纲以便计算和比较

(16)

式中Nn(c,a)——从栅格单元c到a的第n个无量纲的单因素成本

Cn(c,a)——从栅格c到a的第n个单因素步行成本，如S、Dh、Ds、T、Q、L、G等

Cnmax——第n个单因素影响下栅格间的最大成本

随后将n个无量纲的单因素成本按指定权重加权组合为综合步行成本

(17)

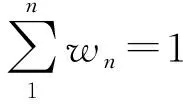
(18)

式中wn——第n个单因素成本所占的权重

2.3 林区步行栅格网络模型构建

林区步行栅格网络模型仅考虑可行与易行栅格8方向邻域的拓扑关系，是一类稀疏有向加权图。因此，采用邻接表表示栅格网络，以避免存储冗余、提高计算效率并支持邻接关系的动态创建。算法步骤如下：

(1)输入数据和参数。输入CWR、DEM、LCR、LIPR等基本栅格数据；单因素成本数n；成本类型K1,K2,…,Kn及其权重w1,w2,…,wn。

(2)算法初始化。按顺序编号CWR栅格单元，构建邻接表，将可行和易行栅格作为头结点插入邻接表。如图3所示，扩展表节点数据域为长度为n的一维数组，存储从栅格c到a的第n个单因素成本Cn(c,a)。另外，构建长度为n的一维数组储存第n个单因素成本的最大值Cnmax，初始值设为极小值MIN。

(3)邻接关系构建与单因素成本计算。遍历邻接表头结点，建立其对应栅格c与邻域八方向可行或易行栅格a的邻接关系，构造表结点插入邻接表。计算K1,K2,…,Kn的单因素成本Cn(c,a)。若Cn(c,a)>Cnmax，则Cnmax=Cn(c,a)。

(4)综合步行成本计算。遍历邻接表，提取Cnmax利用式(16)对表结点中的n个单因素成本Cn(c,a)进行标准化，进而结合输入的权重w1,w2,…,wn利用式(17)计算综合步行成本，储存于邻接表表结点的数据域中。

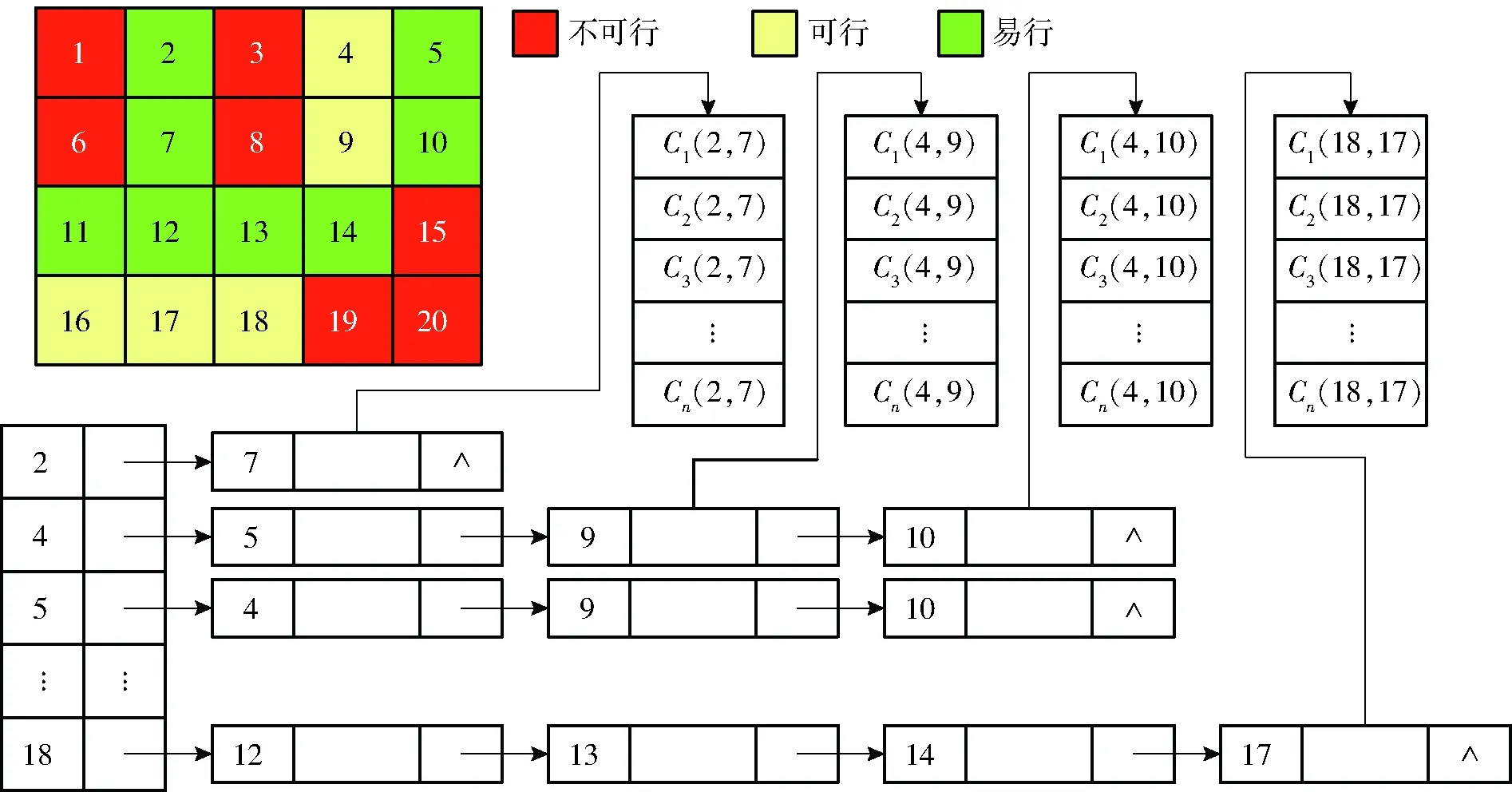
图3 基于扩展邻接表的栅格网络模型Fig.3 Raster network model based on expanded adjacency list

基于CWR建立的栅格网络模型融合了地表可步行性与步行寻路目标，能够表示混合空间中的寻路需求，将林区步行最优路径分析转换为传统网络分析问题，引入成熟的网络分析算法进行求解。本研究利用Dijkstra算法基于栅格网络模型计算最优路径。

3 试验结果与分析

本文以北京林业大学实验林场局部区域为试验区。试验区面积2.65 km2，高程166～1 005 m。试验数据包括网格DEM数据(分辨率5 m×5 m)、森林资源二类调查数据、公路、小径、地标以及不可行地物(密林、巨石、建筑物等)。基于ArcGIS Runtime SDK for .NET，采用C语言实现相关方法。以空间距离K1、步行时间K2、体能消耗K3、灌木盖度K4和地标可视成本K5为优化目标，利用Dijkstra算法计算最小成本路径，验证方法的有效性。

3.1 基于CWR的栅格网络模型构建试验

以坡度大于45°和不可行地物所在的区域为不可行域，公路、小径为易行域构建综合可步行性栅格，在此基础上输入DEM、LCR、LIPR，建立存储单因素步行成本的栅格网络模型。图4为指定路径起点、终点的单目标步行最优路径分析结果，P1～P5分别为以K1～K5为优化目标计算的最小成本路径。可见，所有路径均能回避不可行域。由于P1、P2、P3仅考虑地形成本，为开放空间中的越野路径。P4、P5仅考虑地物成本，部分路段为开放空间中的越野路径，其余路段覆盖了道路网络，尽管P5距离最长，但超过80%的路径单元为易行栅格，这是由于易行域能够减少覆盖物和地标可视成本。说明基于CWR构建的栅格网络模型能够充分考虑不同环境因素对地表可步行性的影响，兼顾开放空间和道路网络，对步行环境的复杂性进行有效的建模。

图4 单目标步行最优路径分析结果Fig.4 Results of single objective optimal walking path analysis

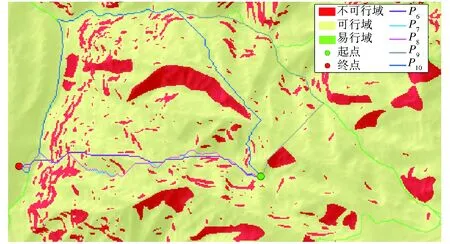
图5 多目标步行最优路径分析结果Fig.5 Results of multi-objectives optimal walking path analysis

3.2 多目标步行最优路径分析试验

如图5所示，分别以K1～K5为主要目标，其余为次要目标构建综合步行成本，计算多目标步行最优路径P6～P10。表1为路径P1～P10的权重分配与单因素成本。对比可见，多目标路径中主要目标的成本均略微高于对应单目标路径的成本。与此同时，大部分次要目标的成本出现了较大幅度的下降，其中路径P7的目标K5降幅最大(57.47%)，平均降幅超过1/4(25.66%)。说明本方法能够在保持主要优化目标成本不显著增加的同时有效降低多个次要目标的成本。另外，P6的K2、K3，P7的K3，P8的K2和P9的K5的成本出现了小幅上涨(平均不超过10%)，这是由于不同成本间具有一定相关性，如地形成本K1、K2、K3均由距离和坡度计算得到，地物成本K4、K5均可受到易行域影响而降低。因此，随着主要目标成本的上涨，个别与之相关的次要目标的成本也可能小幅上涨，但涨幅有限，对整体路径结果的影响较小。

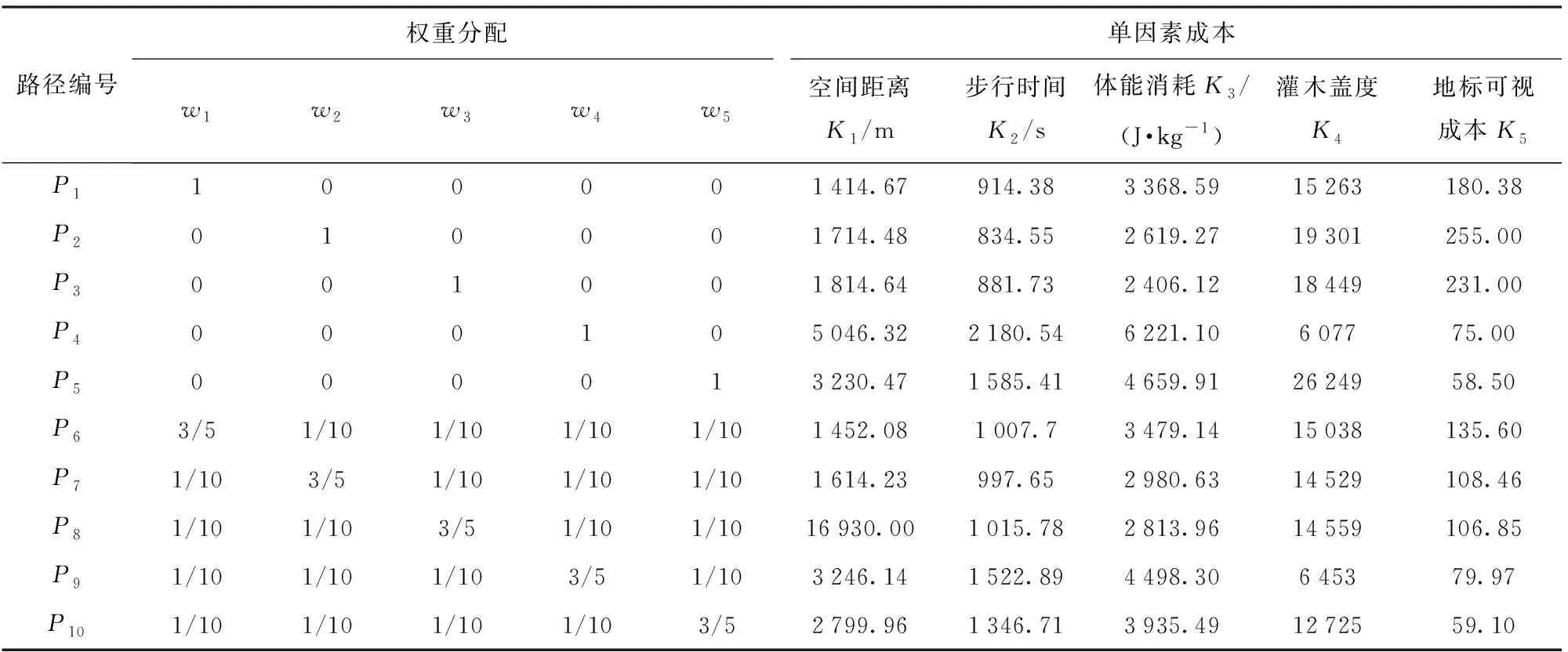
表1 步行最优路径分析的参数与结果Tab.1 Parameters and results of optimal walking path analysis

图6为P1～P10的单因素成本雷达图，坐标轴为K1～K5的单因素成本，成本越小说明方法对该目标的优化效果越好。对比可见，本方法能够有效降低多个优化目标的路径成本，并能通过调整权重使结果侧重于主要目标。另外，从几何形状和单因素成本来看，P2与P3、P7与P8之间具有较高的相似度，同样是由K3、K4间的相关性造成。因此，在选择优化目标时，K3、K4按需求选择其一即可。

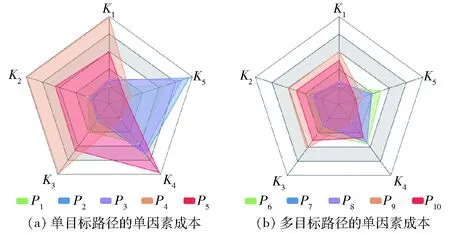
图6 P1～P10的单因素成本雷达图Fig.6 Single cost radar charts of P1～P10

3.3 林区步行最优路径模拟试验

为了验证方法的适用性，本文模拟了3类林区步行寻路需求，综合可步行性栅格的构建条件与路径优化参数如表2所示。P11模拟野外救援人员的寻路需求，偏重步行时间；P12模拟林业工作人员的寻路需求，平衡体能消耗和灌木盖度；P13模拟登山者的寻路需求，强调安全性。

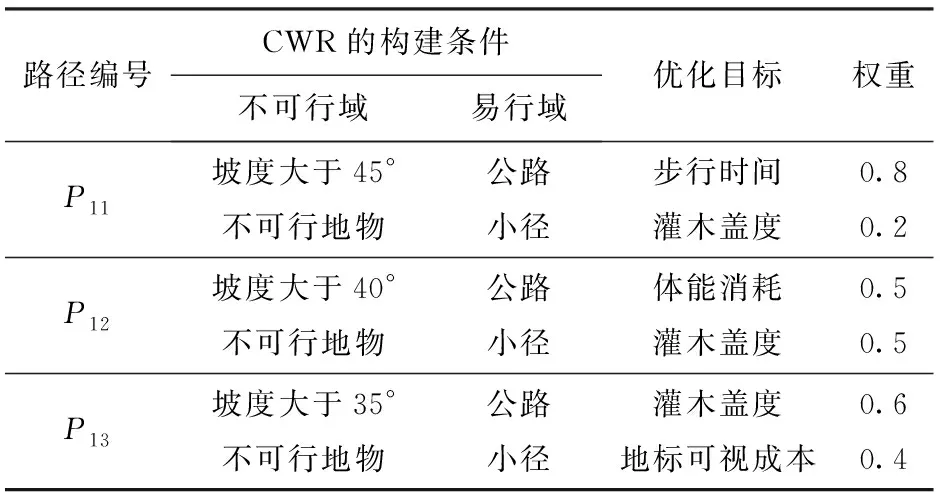
表2 模拟试验条件与参数Tab.2 Conditions and parameters of simulation experiment

图7 模拟3类寻路需求的步行最优路径分析结果Fig.7 Optimal walking path analysis results of simulated three types of wayfinding needs

图7为模拟3类寻路需求的步行最优路径分析结果。由于在建立栅格网络模型的过程中判断栅格单元的可步行性，3条路径均能有效避让不可行域。救援人员自身越野能力较强，能够通过大多数的野外环境，不可行域的面积最小，P11主要是以越野的方式抵达终点，具有较短的步行时间；登山者的越野能力最弱，不可行域的范围最广，虽然P13的距离较远，但超过80%的路径单元覆盖了易行栅格，灌木盖度与地标可视成本较小；林业工作人员介乎前两者之间，P12首先找到最近的易行栅格，随后沿道路行走抵达终点，兼顾了体能消耗和灌木覆盖成本。综上所述，本方法能够生成适应行人通行能力的综合可步行性栅格，在此基础上针对优化目标和权重分配建立栅格网络模型，进而计算最优步行路径，具有一定的适用性。

4 结论

(1)分析了林区步行活动的特殊性，提出了林区步行最优路径分析方法。通过引入可步行性的概念，将林区步行环境定性划分为可行域、不可行域和易行域，将林区步行最优路径分析问题转化为避让不可行域、在可行域与易行域中计算多目标最小成本路径的问题，为解决林区步行寻路问题提供了新的思路。

(2)提出了基于综合可步行性栅格的栅格网络模型构建方法。试验结果表明：栅格网络模型能够融合开放空间与道路网络，对混合空间进行有效的建模。

(3)提出了融合地形成本与地物成本的综合步行成本计算方法，将多目标优化问题简化为单目标问题。试验结果表明：该方法能够有效降低多个优化目标的路径成本，并能通过调整权重使结果侧重于主要目标，具有一定的适用性。

1 陈玥璐, 武刚, 陈飞翔. 基于地标的行人导航路径引导方法[J]. 地理与地理信息科学, 2015, 31(1):17-22.

CHEN Yuelu, WU Gang, CHEN Feixiang. Route directions method of pedestrian navigation based on landmark[J]. Geography and Geo-Information Science,2015,31(1):17-22. (in Chinese)

2 CIESA M, GRIGOLATO S, CAVALLI R. Analysis on vehicle and walking speeds of search and rescue ground crews in mountainous areas[J]. Journal of Outdoor Recreation & Tourism, 2014(5-6):48-57.

3 严瑞, 龙毅, 郑玥,等. 顾及地形起伏的步行最优路径分析算法[J]. 武汉大学学报：信息科学版, 2012, 37(5):564-568.

YAN Rui, LONG Yi, ZHENG Yue, et al. An optimal walking path algorithm considering terrain influence[J]. Geomatics and Information Science of Wuhan University, 2012, 37(5):564-568. (in Chinese)

4 张星, 李清泉, 方志祥. 面向行人导航的地标链生成方法[J]. 武汉大学学报：信息科学版, 2010, 35(10):1240-1244.

ZHANG Xing, LI Qingquan, FANG Zhixiang. An approach for generating landmark chain for pedestrian navigation applications[J]. Geomatics and Information Science of Wuhan University, 2010, 35(10):1240-1244. (in Chinese)

5 张星, 李清泉, 方志祥,等. 顾及地标与道路分支的行人导航路径选择算法[J]. 武汉大学学报：信息科学版, 2013, 38(10):1239-1242.

ZHANG Xing, LI Qingquan, FANG Zhixiang, et al. Landmark and branch-based pedestrian route complexity and selection algorithm[J]. Geomatics and Information Science of Wuhan University, 2013, 38(10):1239-1242. (in Chinese)

6 周沙, 王润, 甄文杰. 顾及主观判断延误的行人路径选择模型[J]. 计算机应用, 2016, 36(4):1146-1150.

ZHOU Sha, WANG Run, ZHEN Wenjie. Pedestrian route choice model considering subjective judgment delay[J]. Journal of Computer Applications, 2016, 36(4):1146-1150. (in Chinese)

7 FANG Z X, LI Q Q, ZHANG X. A multiobjective model for generating optimal landmark sequences in pedestrian navigation applications[J]. International Journal of Geographical Information Science, 2011, 25(5):785-805.

8 刘震, 余洋, 李建松,等. 面向路径优化的变分辨率栅格成本表面模型建模方法[J]. 测绘学报, 2014, 43(5):474-480.

LIU Zhen, YU Yang, LI Jiansong, et al. A variable-resolution raster cost surface model for path optimization[J]. Acta Geodaeticaet Cartographica Sinica, 2014, 43(5):474-480. (in Chinese)

9 ANTIKAINEN H. Using the hierarchical pathfinding A*algorithm in GIS to find paths through rasters with nonuniform traversal cost[J]. ISPRS International Journal of Geo-Information, 2013, 2(4):996-1014.

10 鲁敏, 张金芳. 栅格地形的最优路径分析[J]. 武汉大学学报：信息科学版, 2010, 35(1):59-63.

LU Min, ZHANG Jinfang. Least-cost path analysis in raster terrains[J]. Geomatics and Information Science of Wuhan University, 2010, 35(1):59-63. (in Chinese)

11 BALSTROM T. On identifying the most time-saving walking route in a trackless mountainous terrain[J]. Geografisk Tidsskrift-Danish Journal of Geography, 2002, 102(1):51-58.

12 REES W G. Least-cost paths in mountainous terrain[J]. Computers & Geosciences, 2004, 30(3):203-209.

13 鲁敏, 张金芳, 吕品,等. 基于平均视距的最优可视覆盖路径[J]. 计算机辅助设计与图形学学报, 2007, 19(9):1159-1165.

LU Min, ZHANG Jinfang, LÜ Pin, et al.Optimal visual coverage path based on average horizon[J]. Journal of Computer-Aided Design & Computer Graphics, 2007, 19(9):1159-1165. (in Chinese)

14 LU M, ZHANG J F, LÜ P, et al. Least visible path analysis in raster terrain[J]. International Journal of Geographical Information Science, 2008, 22(6):645-656.

15 CHIOU C R, TSAI W L, LEUNG Y F. A GIS-dynamic segmentation approach to planning travel routes on forest trail networks in Central Taiwan[J]. Landscape & Urban Planning, 2010, 97(4):221-228.

16 TOMCZYK A M, EWERTOWSKI M. Planning of recreational trails in protected areas: application of regression tree analysis and geographic information systems[J]. Applied Geography, 2013, 40(2):129-139.

17 SITZIA T, RIZZI A, CATTANEO D, et al. Designing recreational trails in a forest dune habitat using least-cost path analysis at the resolution of visitor sight distance[J]. Urban Forestry & Urban Greening, 2014, 13(4):861-868.

18 戴冰武, 曾丽婷, 韩西丽. 基于生态安全格局的风景区游览线路最低成本路径选线——以湖南省平江县福桶山景区为例[J]. 现代城市研究, 2015(1):97-103.

DAI Bingwu, ZENG Liting, HAN Xili. Lowest cost path selection of scenic tour route based on ecological security pattern: a case study of Pingjiangbaishui lake Futong hill scenic spot, Hunan[J]. Modern Urban Research, 2015(1):97-103. (in Chinese)

19 邓浩,宋峰,蔡海英.城市肌理与可步行性——城市步行空间基本特征的形态学解读[J].建筑学报,2013(6):8-13.

DENG Hao, SONG Feng, CAI Haiying. Urban tissue and walkability morphological analysis on the essential characteristics of urban walkable space[J]. Architectural Journal, 2013(6):8-13. (in Chinese)

20 NASIR M, LIM C P, NAHAVANDI S, et al. Prediction of pedestrians routes within a built environment in normal conditions.[J]. Expert Systems with Applications, 2014, 41(10):4975-4988.

21 周成虎, 裴韬. 地理信息系统空间分析原理[M]. 北京：科学出版社, 2011.

22 史恩秀, 陈敏敏, 李俊,等. 基于蚁群算法的移动机器人全局路径规划方法研究[J/OL]. 农业机械学报, 2014, 45(6):53-57. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20140609&journal_id=jcsam. DOI:10.6041/j.issn.1000-1298.2014.06.009.

SHI Enxiu, CHEN Minmin, LI Jun, et al. Research on method of global path-planning for mobile robot based on ant-colony algorithm[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(6):53-57. (in Chinese)

23 刘建华, 杨建国, 刘华平,等. 基于势场蚁群算法的移动机器人全局路径规划方法[J/OL]. 农业机械学报, 2015, 46(9):18-27. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20150903&journal_id=jcsam. DOI: 10.6041/j.issn.1000-1298.2015.09.003.

LIU Jianhua, YANG Jian’guo, LIU Huaping, et al. Robot global path planning based on ant colony optimization with artificial potential field[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(9):18-27. (in Chinese)

24 张文,刘勇,张超凡,等. 基于方向A*算法的温室机器人实时路径规划[J/OL]. 农业机械学报,2017,48(7):22-28.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20170703&journal_id=jcsam. DOI: 10.6041/j.issn.1000-1298.2017.07.003.

ZHANG Wen, LIU Yong, ZHANG Chaofan, et al. Real-time path planning of the greenhouse robot based on directional A*algorithm[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2017,48(7):22-28. (in Chinese)

25 KAY A. Pace and critical gradient for hill runners: an analysis of race records[J]. Journal of Quantitative Analysis in Sports, 2012, 8(4):1-18.

26 MINETTI A E, MOIA C, ROI G S, et al. Energy cost of walking and running at extreme uphill and downhill slopes[J]. Journal of Applied Physiology, 2002, 93(3):1039-1046.

27 BROSSET D, CLARAMUNT C, SAUX E. Wayfinding in natural and urban environments: acomparative study[J]. Cartographica the International Journal for Geographic Information &Geovisualization, 2008, 43(1):21-30.

28 KETTUNEN P, IRVANKOSKI K, KRAUSE C M, et al. Landmarks in nature to support wayfinding: the effects of seasons and experimental methods[J]. Cognitive Processing, 2013, 14(3):245-253.

29 KETTUNEN P, SARJAKOSKI L T. Empirical construction of a landmark ontology for wayfinding in varying conditions of nature[C]∥The Agile International Conference on Geographic Information Science, 2015.

30 鲁敏,张金芳,范植华,等. 基于地形可视性分析的最优路径搜索[J].系统仿真学报, 2008, 20(10):2601-2605.

LU Min, ZHANG Jinfang, FAN Zhihua, et al. Least-cost path planning based on rerrainvisibility analysis[J]. Journal of System Simulation, 2008, 20(10):2601-2605. (in Chinese)