中国经济周期波动福利成本的估算

何林浩

一、引言

“一收就死，一放就乱”是很多政策面临两难境地的真实写照，高增长一般伴随着高波动，是要更小的经济波动还是更高的长期经济增长率？Lucas（1987， 2003）［1-2］认为微观数据显示了消费者都是风险厌恶者，因此经济波动越大，经济周期的福利成本越大。令很多经济学家诧异的是，Lucas使用美国1947—2001年的消费数据进行分析时发现，经济周期的福利成本仅为0.05%，这说明经济波动对消费者的福利影响并不是很大。这一估计结果震惊了很多经济学家，这说明经济学家应该把更多的精力投入到经济增长等更重要的问题上。

Lucas的分析结果虽然在学术界影响颇大，但难以取得政策制定人士的共鸣，政策制定人士显然认为经济波动对居民福利的损害远大于Lucas的计算结果。Lucas也注意到了他文章中存在的问题，Lucas（1987）［1］在这篇文章的注脚中写道：“将商品消费的不稳定和一般经济的不稳定二者混为一谈也是不准确的，因为闲暇的消费也会波动。但由于工作时数与商品消费是周期正相关的，我猜测更加仔细地将闲暇波动也考虑在内将进一步降低文中的估计”。也就是说Lucas认为加入闲暇时间 （全部时间＝闲暇时间＋劳动时间）不会改变文章的基本结论。然而King和Rebelo（1999）［3］发现劳动时间的对数标准差是消费的对数标准差的1.3倍左右，因此忽视劳动时间的波动来计算经济周期波动的福利损失很可能会使得计算结果偏小。

本文试图对Lucas基本模型进行修正，通过定量的数值计算方法来估算中国经济周期波动的福利损失，为这种政策上的左右为难提供分析框架和政策建议。本文的分析具有重要的理论和政策价值：首先，把劳动时间的波动加入到经济周期成本的评估之中，模型使得经济周期成本的计算脱离了风险规避系数的束缚，本文认为经济周期波动成本的分析应该着重研究周期波动对资源配置的影响；经济周期波动的过程就是对均衡状态偏离的过程，在这个过程中会存在资源错配，而这种资源错配所造成的损失就是经济周期波动的成本，就业率对经济波动的敏感性大小决定了经济周期波动对居民福利的损害程度。其次，考虑到中国目前的改革进入深水区，过于快速的改革可能造成经济的波动，过慢的改革又会降低潜在经济增长率，本文为经济体制改革的速度选择问题提供了理论参考。

本文的结构如下：第二部分对相关文献进行综述；第三部分，建立一个包含劳动时间波动的经济周期成本估算模型，使得经济周期成本的模型结果完全摆脱了风险规避系数的束缚；第四部分对模型进行了具体的数值计算，考虑到部分居民承担总劳动时间波动的情况，并把经济周期波动的福利损失与提高经济增长率的收益进行比较；第五部分为本文的总结。

二、相关文献回顾

近年来国内外的相关文献层出不穷，对于经济周期波动对居民福利影响的大小依然存在争论，有模型设计上的争论也有数据方面的争论。

许多经济学家试图从效用函数形式的修正来推翻Lucas的基本结果，但大多数研究成果都严重依赖于风险规避系数的大小，然而微观数据表明风险规避系数很难取很大的值。 Mehra和 Presscott（1985）［4］发现在CRRA框架之下，要解释股权溢价就必须使得风险规避系数达到40以上，但在个人投资组合以及高风险行业收益溢价等实证案例中，很难找到与之相匹配的风险厌恶水平。部分经济学家通过使用三个参数的效用函数来放松微观数据对风险规避系数的束缚。CRRA效用函数是时间可加和状态可分的，Lu⁃cas的结论依赖于标准的CRRA效用函数和美国相对平滑的时间序列数据，后续的研究经济周期成本的文献主要从采用较大的风险规避系数、修改效用函数、使用其他国家的消费数据等角度对Lucas的结论进行修正和完善。 Tallarini（2000）［5］以及 Epstein和 Zin（1991）［6］等人研究基于递归效用函数的福利成本模型，他们发现经济周期的福利成本显著大于Lucas模型估计的水平； Wincoop （1994）［7］认为居民消费存在很强的习惯性的特征，他在Lucas模型基础上引入消费习惯因素，同样发现经济周期的福利成本远远大于Lucas模型估计的水平。这些对模型的修改虽然能得到更大的经济周期成本，但会带入一些其他的问题。

Lucas在文中提到的对闲暇波动 （总时间＝闲暇时间＋劳动时间）的忽视似乎并没有引起其他经济学家的兴趣，他认为文中的模型将商品消费的不稳定和一般经济的不稳定 “混为一谈”，但他进一步认为仔细地将闲暇波动也考虑在内将进一步降低文中的估计。虽然部分文献也注意到了异质性可能对估计结果产生影响，但是更多的分析集中于对消费异质性的影响， 比如 Krusell和 Smith （1999）［8］对这种可能性进行了分析，他们发现个体差异性对消除总体风险带来的收益的估计影响不大，他们的模型估计的估计值对很多参数的设置非常敏感，又比如 Storesletten等（2001）［9］使用了世代交叠模型研究异质性对经济周期成本的影响，他们的一个重要结论是经济周期成本与风险规避系数不成比例。

目前中国经济学家对经济周期波动福利损失的研究还相对较少，并且大多数研究还是对国外已有的模型加入中国数据的重新计算，但分析的结果同样过度依赖于风险规避系数，并且忽略了劳动时间波动对结果的影响。陈彦斌 （2005）［10］运用2001年1季度到2003年4季度中国数据，估计了中国经济周期的福利成本，结果显示，与美国相比中国经济周期波动的福利成本将增加几倍，但仍然不到1个百分点。陈太明 （2007）［11］运用Lucas的模型，计算了改革开放之后中国经济周期的福利成本，其结果表明：在风险规避系数合理取值范围内，经济周期的福利成本非常小。也有文章对增长和稳定的收益进行了比较，饶晓辉和廖进球 （2008）［12］运用中国1978—2004年度数据分别计算了经济周期波动的成本和提高经济增长率的收益，其结果表明，对于合理的偏好参数，中国经济波动的福利成本与经济增长的福利收益两者数值相对比较接近。另外的文章有李凌和王翔（2010）［13］， 张耿 （2016）［14］和黄梅波和吕朝凤（2011）［15］等等。

本文认为经济周期波动对居民造成的伤害不仅仅在于其导致的消费波动，主要在于经济周期波动导致的就业率波动。本文把劳动时间的波动加入到模型中，之后继续以一般商品消费的补偿比例作为经济周期成本的衡量指标，研究这种改变是否会增大经济周期成本的估计值；此外，现有文献对经济周期波动的福利损失估计值过度依赖于风险规避系数，本文将考察加入劳动时间后是否能够使得经济周期成本摆脱风险规避系数的束缚。本文利用了中国宏观数据进行数值计算，这对中国政府目前推进改革速度的选择具有参考意义。

三、理论模型：Lucas基准模型的拓展

要计算经济周期波动的福利成本，就必须先理解什么是经济周期波动。本文中的经济周期波动是指，某种刚性或粘性使得经济不能有效地对名义冲击或者实际冲击做出反应，进而偏离经济均衡水平的过程。经济周期波动不仅会造成消费的波动，而且会造成劳动时间的波动，而且劳动时间的波动远大于消费的波动。毫无疑问，如果真实经济周期理论的主张是正确的，那么计算经济周期的成本将毫无意义。

虽然后来的研究对Lucas的分析框架进行了拓展，加入了很多其他的因素，但从目前来看，Lucas模型依然是迄今为止最为稳健的基准模型，并且Lu⁃cas认为加入其他因素来解决问题的同时，可能会带来更多的问题，因此下面的模型拓展依然建立在Lu⁃cas基准模型之上。

（一）模型的建立

评估经济周期波动对居民的影响，就必须了解居民的效用函数形式。假设经济中拥有大量的无限生命的个体，他们的期望效用函数定义为：

式 （1）是最为常用的预期效用函数形式。其中，β为贴现因子，0＜β＜1，Ct为消费，Lt为劳动时间，E0为对未来消费Ct和未来劳动时间Lt的效用的期望，期望效用函数关于消费和劳动时间的变化是平滑的。

假设存在两种经济状态A和B，A代表经济永远处于长期均衡的状态，没有外在冲击使其产生波动；B代表现实中的经济状态，产出围绕长期趋势进行波动。A状态的居民福利大于B状态的居民福利，这种福利的损失就是经济周期的福利成本。

如何来评估经济周期的成本？评估对居民福利影响的方法有多种，比如，可以用时间的补偿而非商品消费的补偿作为经济周期成本的指标。Lucas采取的方法是，使得B状态的效用值达到A状态所要求的消费量补偿比例，后来的研究基本都采用这一方法。本文同样采用消费量的补偿比例作为经济周期成本的衡量指标，即：

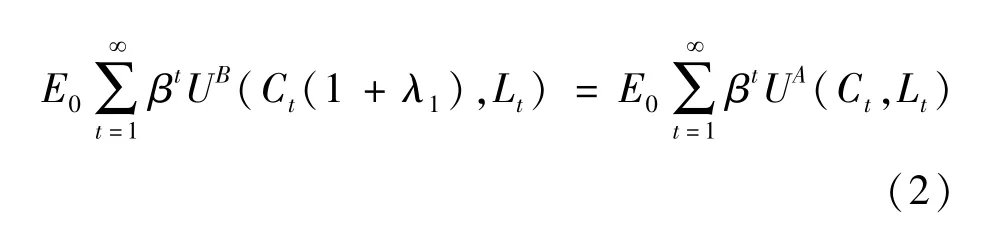
式 （2） 与 Lucas （2003）［2］的方法类似。 式中的λ1即得出经济周期的成本，用占全部消费品的百分比表示。

长期的时间序列数据显示，消费和劳动的跨期替代弹性都是比较稳定的，因此本文引入一个不变弹性的效用函数。居民的效用取决于消费量和劳动时间，一个人一生的效用取决于其一生所消费的商品和一生的劳动时间，不变弹性效用函数的基本形式为：

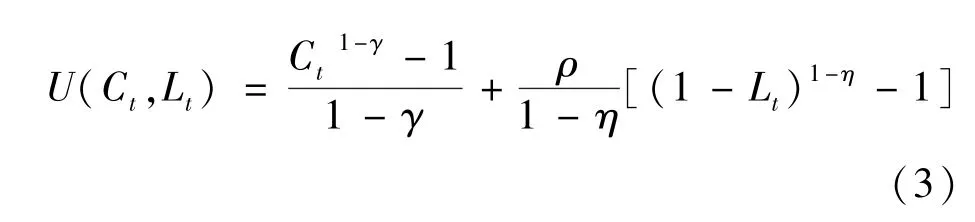
（3）式中的效用函数形式广泛应用在经济增长模型中以及真实经济周期模型中。其中，γ为风险规避系数，也是消费的跨期替代弹性的倒数，η为劳动供给的跨期替代弹性，ρ为固定参数，居民的效用取决于商品的消费量和劳动时间，将居民在每一时期的总时间单位化为1。

根据本文对经济周期波动的定义，消费量围绕着一个长期趋势波动，因此对消费流采用与Lucas同样的假设；人均均衡劳动时间不会随着工资率的变化而变化，围绕着一个平均值波动。因此可以假设消费和劳动时间符合下面的随机过程，即：

其中，Ct为t期的实际消费量，Lt为t期的劳动时间，1－Lt为闲暇，μ代表消费的增长率。其中lnut和lnvt属于独立同分布的随机过程，即， 其中， 这样消费的预期值为， 闲暇的预期值为E （1－Lt） ＝A2。

把不变弹性的效用函数 （3）带入到评估公式（2）中，可以得到一个包含经济周期成本指标λ的等式

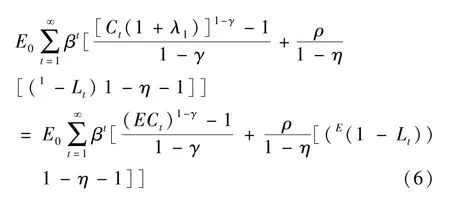
经济周期波动的福利成本λ1取决于消费的波动、劳动时间的波动，以及其他的一系列参数：风险规避系数γ、劳动的跨时替代弹性η和固定参数ρ等。显然，消费的风险规避系数和消费的方差不是经济周期成本的仅有的两个决定性因素，这与Lucas以及其他一些经济学家的模型结果不同。

（6）式很难计算出一个易于理解的值，需要做一定的简化。很多研究基于一系列微观经济的数据，对效用函数采用了双对数的形式，本文也采取这种形式，其中风险规避系数γ和劳动供给弹性的决定参数η都为1，采用洛必达法则，对 （3）式两边取极限，即可得出新的效用函数形式，即：

（7）式中参数的定义与 （3）式相同。把效用函数以及消费和劳动时间的随机过程带入评估公式，得到经济周期波动的福利成本为：

重新计算的经济周期波动的福利成本λ1取决于消费的波动、劳动时间的波动以及ρ。

显然，消费的风险规避系数 （本文已假设风险规避系数为1）和消费的方差不是经济周期成本仅有的两个决定性因素，经济周期波动的成本还取决于闲暇的波动也即劳动时间的波动，以及闲暇效用的技术参数。

令人惊讶的是，经济周期波动的成本可以被拆分为闲暇波动 （与劳动时间的波动相关）的成本和消费波动的成本。当实际劳动时间大于均衡劳动时间时，闲暇消费的边际效用大于一般商品消费的边际效用，当实际劳动时间小于均衡劳动时间时，闲暇消费的边际效用小于一般商品消费的边际效用，这两种情况都会产生福利损失。因此，本文模型描述的经济周期成本是资源错配的福利损失，经济波动成本的大小取决于资源错配的程度。

（二）与Lucas基准模型的比较

Lucas首次对经济周期福利成本进行了模型化的规范分析，Lucas认为居民是风险厌恶的，对于波动的消费流和平滑的消费流，居民更偏好后者，因此消费的波动是存在成本的，可以近似地把消费的波动等同于经济的周期波动，因此经济周期的福利成本就是消费波动的成本。Lucas基准模型的逻辑图示如图1。

图1 Lucas基准模型的简化图示

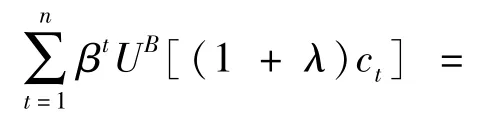
对于居民来说，劳动时间的选择取决于闲暇的边际效用和消费品边际效用的比较，如果经济偏离均衡状态向上波动，居民的工作量增加，闲暇的消费减少，商品消费增加，在偏好不变的情况下，闲暇的边际效用大于商品消费的边际效用，居民对于商品与闲暇的选择处于非均衡状态，而均衡状态是最优状态，因此此时的非均衡状态是存在效用损失的，同理，经济偏离均衡状态向上波动也会产生效用损失。也就是说，经济波动会产生一种持续的对资源配置的扭曲效应，均衡状态是最优状态，任何偏离均衡状态的情形都会产生福利损失，不管居民的风险态度是怎样的，经济向上偏离均衡值或向下偏离均衡值都是存在效用损失的，因此经济周期波动产生一种资源错配的效率损失。

本文模型逻辑的简化图示如下：

图2 本文模型的简化图示

图2中的横轴代表产出的状态值，纵轴为居民的效用值。该图的含义是：横坐标产出状态下对应的纵坐标的代表性居民的效用值。U－表示消费向下偏离均衡状态下，产出为所对应的居民效用值；U＋表示消费向上偏离均衡状态下，产出为所对应的居民效用值；U∗表示均衡状态，产出为时所对应的居民效用值。产出不管是低于均衡状态的产出还是高于均衡状态的产出，居民的效用值都小于U∗，这就是本文模型与Lucas基准模型的不同之处，本文计算的是资源错配的福利损失，这与居民的风险厌恶的态度没有关系。

相对于消费的跨期波动，经济波动导致的资源错配是更大的危害。经济过热后 “一地鸡毛”，我们看到的是大量的无效投资，这些投资的边际收益率太小无法覆盖机会成本，经济衰退时期，我们看到的是大量的产能闲置，大量的劳动力闲置，失业率高于自然失业率，这些都是经济波动的成本，经济波动的成本不仅仅是今天多吃一碗饭明天少吃一碗饭的消费波动的效用损失。因此，本文认为经济周期成本的分析重点应该放到其对资源配置的影响上来。

现实经济中，不仅存在劳动时间和一般商品消费的资源错配，更多的资源错配表现为资源投向了错误的行业，或者资源投资过度以至于投资的边际收益无法覆盖边际成本，这些都是经济周期波动可能导致的福利成本。以 “四万亿”政策为例，其导致了2008年以来的产出增长大幅波动，很多行业产能过剩，如果把这些资源配置到其他行业就能在一定程度上提高居民福利。这些因素暂时不在本文的考虑范围之内，毫无疑问考虑这些因素不仅不会改变本文的主要结论，还会强化本文的观点。

（三）模型的结果分析

由于把全部时间单位化为1，那么闲暇时间和劳动时间的和为1，这样就可以把对数闲暇时间的方差和对数劳动时间的方差联系起来，即：

其中，其中，为均衡劳动时间，为对数闲暇时间的方差，为对数劳动时间的方差，可以通过劳动时间的方差求得闲暇时间的方差。

考虑到居民个体的均衡劳动时间的长期均值是比较稳定的，不会随着劳动工资的变化而变化，ρ就取决于均衡劳动时间的大小。对一个简单的劳动时间模型进行计算 （King和 Rebelo， 1999）［3］， 得出

因此，式 （8）转化为：

总劳动时间的周期变化大部分来自于就业的变化，也就是说总劳动时间的波动是由部分劳动者的劳动时间波动构成，因此一部分人所面临的经济周期波动的福利损失更高，本文将对此进行简单的计算。以一个概率θ作为一个居民被 “选中”承担总劳动时间波动的概率，也就是说总体的居民中有θ比例的人承担了总的劳动时间波动，那么经济周期波动成本的估算公式可以转化为：

相当于：

四、基于中国宏观数据的估算结果

（一）经济周期成本的估算值

本文选取的消费数据是1978—2015年 “全国居民消费水平”经过 “居民消费价格指数”调整过的年度实际消费水平，数据来自 《中国统计年鉴》。

根据 （4）式的消费的随机过程，对实际消费数据进行计算，（4）可转化为：

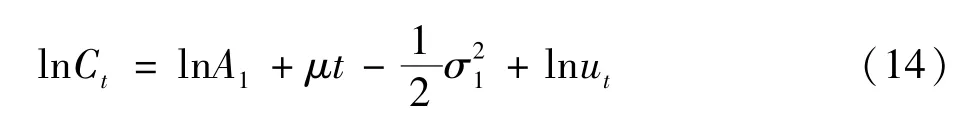
因此，可以建立对数的人均年消费水平对时间的一元回归方程，OLS的估计性质表明，误差项方差的OLS估计是无偏估计，其数值为残差平方和除以（样本数量－2），计算出的对数人均消费水平的标准差为0.052。

同理，为了计算人均劳动时间波动的方差，可以建立对数的人均劳动时数对时间的一元回归方程，然而考虑到中国没有权威的劳动时间的相关数据，并且国企占比非常大，无法显示市场真实的劳动时间波动。以劳动时间统计比较全面的美国来看，对数人均工作时间的方差与对数人均产出的方差大致相同，King和Rebelo （1999）［3］发现对数人均产出的标准差为0.018 1，对数人均劳动时间的标准差为0.017 9，二者相差不大，这主要是由于劳动生产率比较稳定的缘故。鉴于此，本文假设中国的对数人均劳动时间的标准差与对数人均产出的标准差相同，计算出的结果为0.043。

表1 基本结果

表1报告的是假设三种劳动时间均衡值的情况下与Lucas估计值的比较。时，经济周期波动的成本为1.598‰，当时，经济周期波动的成本是1.807‰，当时，经济周期波动的成本为2.437‰。毫无疑问，加入劳动时间的波动会增大经济周期成本的估算值。

（二）部分居民承担总劳动时间波动下的经济周期成本估算

虽然表1的估计值比Lucas的估计结果增大了很多，但在量级上依然很小，主要有两个原因：一是没有考虑部分劳动者承担了总劳动时间波动，周期波动对劳动者影响的异质性可能会影响估计的结果；二是上文只考虑了劳动时间错配的影响，如果考虑到经济周期波动对投资、储蓄以及行业配置的影响，经济周期成本的估计值应该更大，但这方面的分析似乎缺乏相关的有说服力的数据。鉴于此，本文只关注第一个原因对本文估算结果的影响。

依然用上文估算的对数消费方差和对数劳动时间的方差来对 （13）式进行计算。我们很难找到一个确切的值来刻画θ的数值，因为在不同的经济周期中θ是不同的，也许最准确的数值应该是失业率的标准差，但这个指标也存在问题，因为一个居民的劳动时间的变化在经济周期中是不对称的，鉴于此，本文将选择几个数值来分别进行计算，结果如表2。

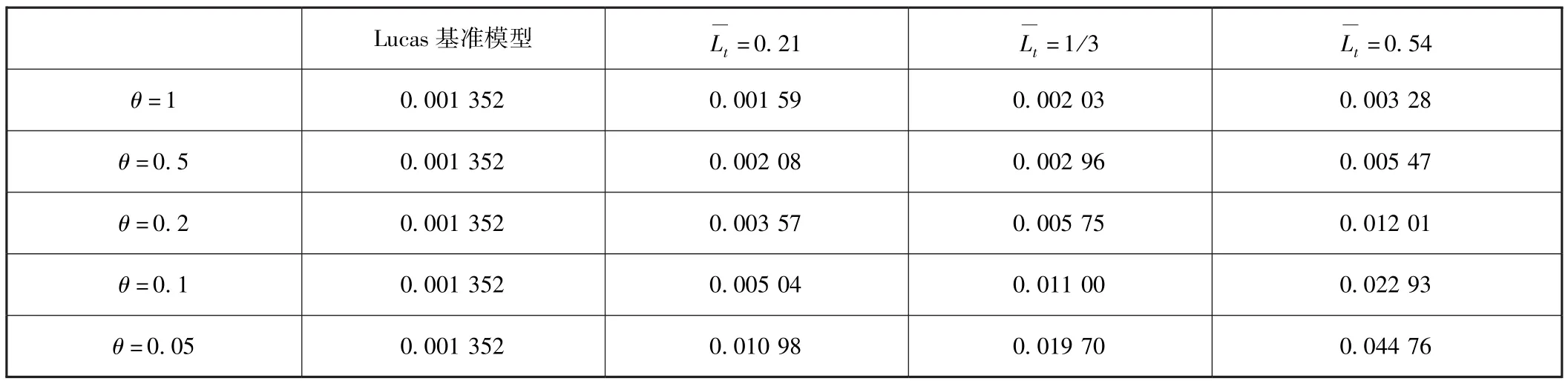
表2 部分居民承担总劳动时间波动

可见，考虑部分人承担总劳动时间的波动后，经济周期成本的估计值会增大很多。当θ＝0.5的时候，经济周期波动的福利损失处于2.08‰到5.47‰之间；而当θ＝0.05的时候，经济周期波动的福利损失处于1.098%到4.476%之间。因此，本文的估算结果更偏向于认为经济周期的福利损失很大，并不是可以忽略不计。

就业率对经济波动的敏感性大小决定了经济周期波动对居民福利的损害程度，所以为什么大多数国家把失业率作为宏观经济政策的一个很重要的目标，而Lucas以及其他一些学者对经济周期成本的研究忽略了这一点，这也是为什么他们的研究都认为经济周期波动对居民福利的损害很小的原因。

（三）与提高经济增长率收益的比较

假设两种经济状态C和D，C代表现实中的经济状态，D代表提高经济增长率后的状态，C状态的居民福利小于D状态的居民福利，这种福利的增加就是提升经济增长率的收益。

式 （15） 取自 Lucas （1987）［1］。 计算出的 λ2是负值，表示提升消费增长率所愿意放弃的消费量比例， －λ2即是所要计算的提升增长率的收益，用占全部消费品的百分比表示，分别为不同经济增长率下的消费。

假设C状态的增长率为μ0，D状态的增长率为μ，增长率的变化是永久性的，而非暂时性的。需要再次强调的是，与以往的文献类似，这里的增长率是消费增长率。计算出的λ2是负值，表示提升消费增长率所愿意放弃的消费量比例， －λ2即是所要计算的提升增长率的收益。

如果采用 （3）式的效用函数，带入到评估方程中，提高增长率的收益即为：

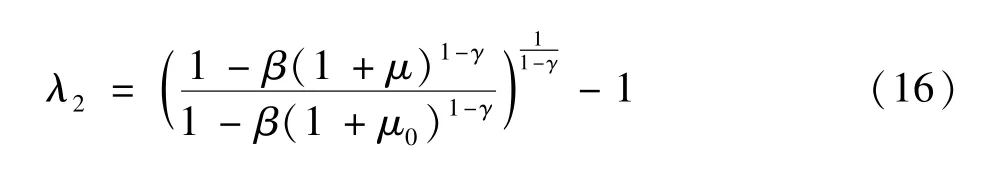
如果采用 （7）式的效用函数，假定风险规避系数为1，提升增长率的收益为：

（16）和 （17）式表明，提升增长率的收益取决于初始增长率、偏离后的增长率、风险规避系数以及主观贴现因子等指标。由于经济增长率的改变不会影响均衡劳动时间，因此劳动时间的波动不会影响估计值。

计算出的λ2是负值，表示提升消费增长率所愿意放弃的消费量比例， －λ2即是所要计算的提升增长率的收益。

为了计算提升经济增长率的收益，必须首先了解在现有条件下的潜在经济增长率是多少，中国经济步入新常态后，前几年的增长率在6到7之间，随着人口结构转变，未来的经济增长率可能更低。本文将对现有条件下的潜在经济增长率取三个不同的值5%、6%和7%，这样的取值与目前中国的增长状态相符合，政府所指定的经济新常态下2016年的增长率目标就是6.5%；经济增长率的变化取0.2、0.5、0.8和1四个不同的值，四个取值都不太大主要是考虑到提升潜在经济增长率的难度，虽然短期提升一两年的增长率可能很容易，但长期增长率的提升则需要政策的彻底性改革；一些微观案例以及资产定价的实证分析表明，风险规避系数在1到10之间是比较合理的，下文的风险规避系数分别取1、2和5三个不同的值，虽然股权溢价悖论认为只有20～40左右的风险规避系数才能解释股市的风险定价，然而这与诸多微观案例相悖。

表3、表4和表5分别是风险规避系数为1、2和5时的值。

表3 风险规避系数＝1

表4 风险规避系数＝2

表5 风险规避系数＝5

以5%增长率作为分析的基准。当风险规避系数为1时，提升增长率的收益为0.017 9到0.164 8，提升增长率0.1个百分点的收益是0.017 9，提升1个百分点的收益是0.164 8；当风险规避系数为2时，提升增长率的收益为0.009 0到0.082 3，提升增长率0.1个百分点的收益是0.009 0，提升1个百分点的收益是0.082 3；当风险规避系数为5时，提升增长率的收益为0.003 4到0.030 8，提升增长率0.1个百分点的收益是0.003 4，提升1个百分点的收益是0.030 8。

可见，其他条件相同时，风险规避系数越大提升增长率的收益越小；基准增长率越大提升增长率的收益越小；但估计值对前者的敏感性大于对后者的敏感性，并且风险规避系数越大，估计值对基准增长率的设定越敏感。

虽然在短期，经济增长会影响就业率，就像“奥肯定律”所描述的，GDP变化和失业率变化之间存在着一种相当稳定的关系，然而从长期来看存在一个 “自然失业率”，失业率围绕着 “自然失业率”波动，由于本文研究的是长期视角的消除经济周期波动的收益和提高经济增长率的收益比较，因此不需要考虑短期经济增长和就业率的相关关系。

要对二者进行比较，有必要对θ和的值进行限定，下面的分析取θ＝0.05和，θ可以看作是就业率对经济波动敏感性的指标，为居民劳动时间的均衡值。

当风险规避系数等于1时，消除经济周期波动的收益大于提升增长率0.2个百分点的收益。考虑到模型中提高的是永久性的增长率，0.2个百分点已经是一个很大的数值。

另外考虑到资产定价领域的一些现象，只有风险规避系数很大才能解释，因此必须考虑风险规避系数的其他取值对二者比较的影响。风险规避系数不等于1时，消除经济波动的收益也即 （6）式的结果难以计算，但可以对 （6）式做一些规范化的判断，简单求导可得：

（18）式很容易证明。这表明，在其他条件不变时，风险规避系数越大，消除经济波动的收益越大，而 （16）式和表3、表4、表5的计算结果表明，风险规避系数越大提高增长率的收益越小。

当风险规避系数取到5的时候，提升增长率1个百分点的收益为0.022 7到0.030 8，而且在γ＝1的情况下，消除经济波动的收益为0.044 7，这要远大于提升增长率1个百分点的收益。可见，此时，消除经济波动的收益远大于提升增长率1个百分点的收益，经济波动不再如Lucas所说的那样无关紧要。

五、结论

Lucas认为经济周期波动的福利损失仅为0.05%，这说明经济波动对消费者的福利影响并不是很大，经济学家应该把更多的精力投入到经济增长等更重要的问题上。如果把这一论断应用到中国的结果就是，中国居民能够容忍更大程度的经济波动，在推进改革的时候应该更为激进。本文的主要工作试图反驳这一论断，基于劳动时间波动的视角对经济周期波动的福利损失进行重新计算和比较，针对中国宏观数据的数值计算显示，计算出中国的经济周期成本达到0.159 8%到0.243 7%，如果考虑到部分人承担了总劳动时间波动，估算值将达到0.208%到4.476%，这远大于Lucas以及其他一些经济学家的估计结果。此外，本文还把消除经济周期波动的收益与提升经济增长率的收益进行比较，发现当就业率对经济波动比较敏感且风险规避系数为5时，消除经济波动的收益远大于提升长期增长率1个百分点的收益。

本文的主要贡献如下：第一，把劳动时间的波动加入到经济周期成本的评估之中，模型使得经济周期成本的计算脱离了风险规避系数的束缚，本文认为经济周期波动成本的分析应该着重研究周期波动对资源配置的影响，经济周期波动的过程就是对均衡状态偏离的过程，在这个过程中会存在资源错配，而这种资源错配所造成的损失就是经济周期波动的成本。第二，就业率对经济波动的敏感性大小决定了经济周期波动对居民福利的损害程度，考虑到中国目前的改革进入深水区，过于快速的改革可能造成经济的波动，过慢的改革又会降低潜在经济增长率，本文为这种权衡提供了分析框架以及初步结果。

本文的结论对于目前中国就业市场的政策和中央政府的宏观经济改革工作均有非常重要的政策启示：

第一，抑制经济波动影响就业波动的传导路径，加强企业窗口指导或推出税收政策，促进企业以减少人均劳动时间而非减少就业数量来应对经济下滑。既然经济周期波动的危害主要取决于就业率对经济波动的敏感性，政府与其以宏观政策来烫平经济波动不如加强就业政策的实施，尤其是对于国有企业，要加强窗口指导、出台补助等激励政策促使企业避免以减少就业人口数量来应对经济放缓，比如在经济放缓的时候把企业的补助或税收政策与其提供的就业数量联系起来。

第二，政府应该对改革导致的不稳定成本和改革提高潜在增长率的收益进行比较，来决定改革的推进速度。中央政府在推进重点领域改革的时候，必须考虑到其可能导致的经济波动，比如目前的金融体制改革，限制非银金融、互联网金融的发展虽然会减小其导致的宏观风险，但也会导致经济过于依赖银行从而抑制经济增长。此外，改变地方政府考核机制，目前政府更加重视经济增长，而忽视了高增长可能导致的高波动，而高波动导致的福利损失要大于高增长带来的收益，因此有必要改变官员考核指标，为地方政府制定增长和波动的双向考核。

当然本文还有诸多方面的不足，模型的推导忽略了其他因素包括失业保险、居民的消费惯性等方面的影响，另外由于缺乏相关数据，笔者对居民劳动时间波动的计算略显草率。未来的研究必须克服这些方面的问题。

［1］Lucas R.E.， Models of Business Cycles ［C］.Basil Blackwell， 1987.

［2］Lucas R.E.， Macroeconomic Priorities ［J］.American Economic Review，2003，93 （1）： 1－14.

［3］King R G，Rebelo S T.Resuscitating Real Business Cycles ［C］.Handbook of Microeconomics，1999，1 （B）： 927－1007.

［4］Mehra R， Prescott E C.The equity premium： A puzzle ［J］.Journal of Monetary Economics，1985，15 （2）： 67－78.

［5］Tallarini T D.Risk⁃sensitive real business cycles ［J］.Journal of Monetary Economics， 2000， 45 （3）： 507 －532.

［6］Epstein L G， Zin S E.Substitution， risk aversion and the temporal behavior of consumption and asset returns： A theoretical framework ［J］.Journal of Political Economy，1991， 99 （2）： 263－286.

［7］Wincoop E V.Welfare gains from international risksharing☆ ［J］.Journal of Monetary Economics， 1994， 34 （2）： 175 －200.

［8］Krusell P， Smith Jr.A A.On the Welfare Effects of Eliminating Business Cycles ［J］.Review of Economic Dynamics，1999，2 （1）： 245 －272.

［9］Storesletten K， Telmer C I， Yaron A.The welfare cost of business cycles revisited： Finite lives and cyclical variation in idiosyncratic risk ［J］.Nber Working Papers，2000， 45 （7）： 1311 －1339.

［10］陈彦斌.中国经济增长与经济稳定：何者更为重要 ［J］.管理世界，2005（07）：16－21.

［11］陈太明.中国经济周期的福利成本：1978—2004［J］.数量经济技术经济研究，2007（01）：22－30.

［12］饶晓辉，廖进球.递归偏好、经济波动与增长的福利成本：基于中国的实证分析 ［J］.经济科学，2008（04）：17－27.

［13］李凌，王翔.中国城镇居民消费增长与波动的福利成本比较 ［J］.数量经济技术经济研究，2010（06）：111－125.

［14］张耿.后高速增长期经济波动的福利成本 ［J］.世界经济研究，2016（09）：17－28.

［15］Hansen G D.Indivisible labor and the business cycle ［J］.Journal of Monetary Economics， 1985， 16 （3）： 309 －327.

［16］黄赜琳.中国经济周期特征与财政政策效应——一个基于三部门RBC模型的实证分析 ［J］.经济研究，2005（06）：27－39.