广义生日攻击的改进

李梦东 邵玉芳 孙玉情 蔡坤锦(北京电子科技学院 北京 00070)(西安电子科技大学通信工程学院 陕西 西安 7007)

0 引 言

在密码分析技术中，碰撞搜索已经得到了广泛的研究，其中较为典型的是广义生日攻击，它是众所周知的生日攻击[1]的推广。广义生日攻击也被称为k-列表问题，定义如下：已知k个列表和一个目标向量的异或结果为目标向量。Wagner首次研究广义生日攻击，对任何范围的k值，他提出一个算法(k-树算法[2])解决k-列表问题，2015年亚密会，Ivica Nikolic提出多碰撞算法[3]提高了算法的复杂度，该算法在处理消极列表方面与k-树算法不同。

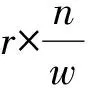
1 已有算法介绍与分析

1.1 k-树算法

Problem1已知k个随机列表和一个随机向量x∈{0,1}n，试寻找x1∈L1,…,xk∈Lk满足x1⊕x2⊕…⊕xk=x，一般情况下x=0。

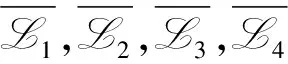
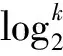
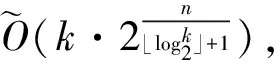
1.2 多碰撞算法

2015年在亚密会上，Ivica Nikolic对Wagner的k-树算法进行了改进，此次改进主要是基于部分多碰撞的思想，使用部分多碰撞算法处理消极列表。换句话说，不再是简单地从消极列表中取出元素，而是从消极列表中找到固定比特位上具有相同值的向量集合。然后，迫使积极列表中的元素在对应的比特位上具有相同的比特。最后，把积极列表和消极列表合并满足剩余的比特位产生碰撞。Ivica Nikolic把23两种情况。接下来详细介绍改进后的3-树算法。

定义1集合S={x1,…,xp}，其中x1,…,xp是n比特的向量。如果lows(x1)=lows(x2)=…=lows(xp)，那么就形成向量末端s比特的部分多碰撞。

图1 改进3-树算法

Kazuhiro Suzuki指出[12]一个集合具有高概率产生多碰撞元素，可以得到：

当然也可以通过一种简单的方式，寻找p的最大值。Kazuhiro Suzuki提出球箱问题，即m个球随机扔进m个箱子里，试寻找那个箱子中的球最多。这个问题的解决方案是公知的，并且最大期望渐近值为：

Ivica Nikolic的多碰撞算法在k值较大(不是2的幂)的情况也是有效的。具体的操作如图2所示，把k个列表分为kA个积极列表和kP个消极列表。

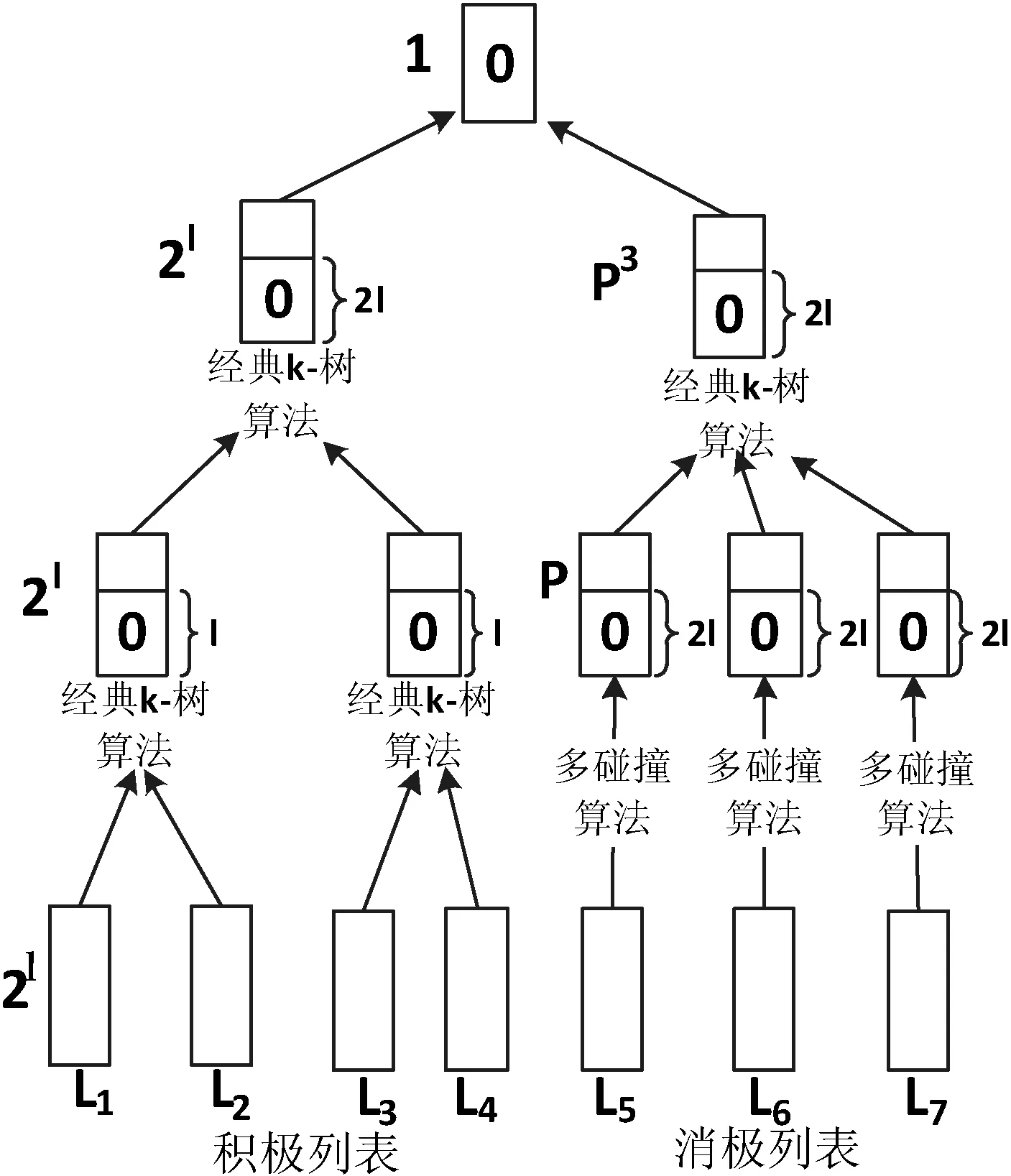
图2 改进的k-树算法(k>3)

因此，相比较经典的k-树算法，改进的k-树算法复杂度之比为:

2 newtree算法介绍

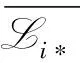
上述的三个列表分别经过Wanger算法产生碰撞值vp，得到列表：

v=v1⊕v2⊕v3,low[3l+1,4l](xip)=vP}

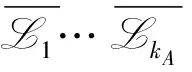
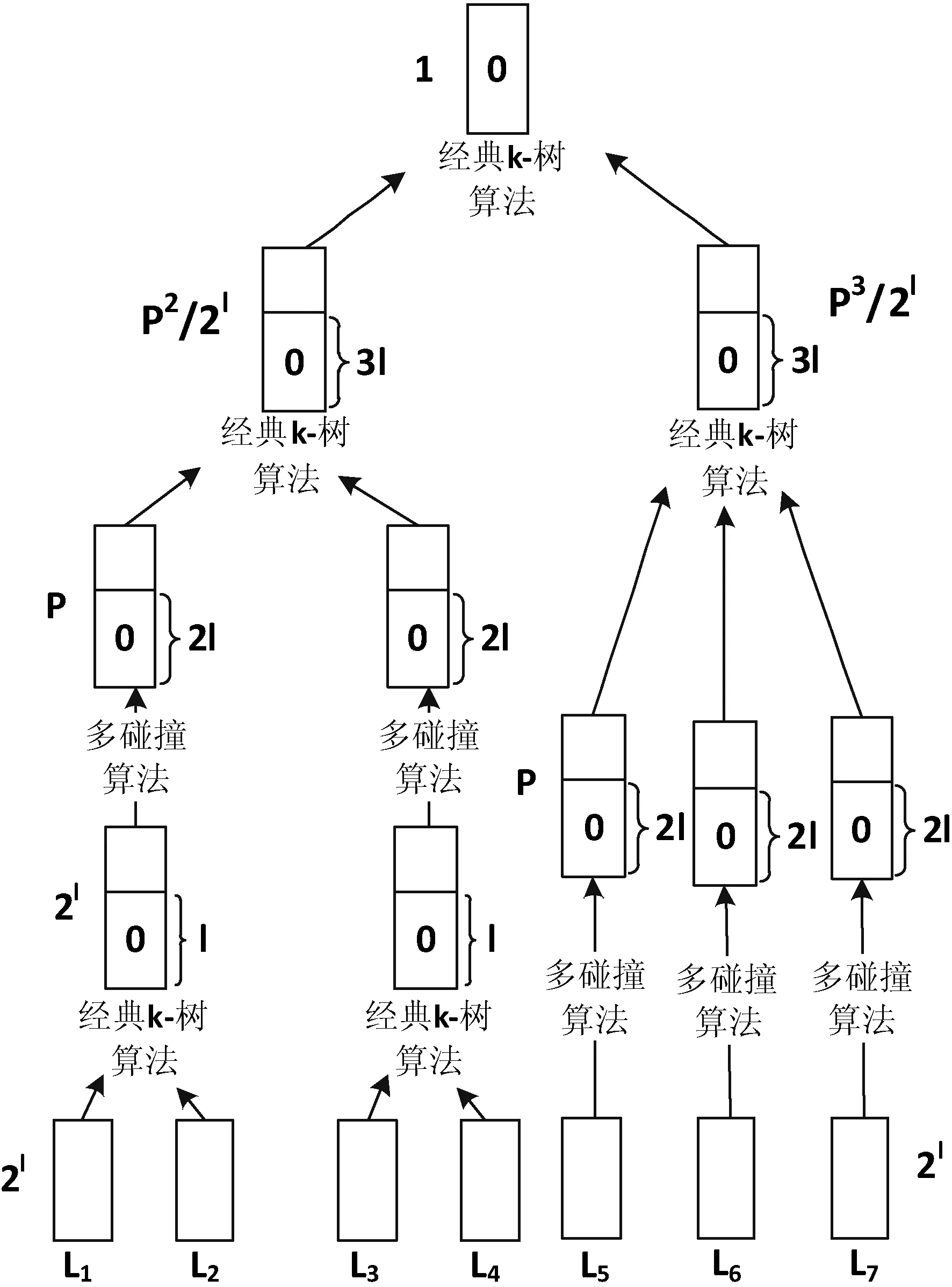
图3 newtree算法(k=7)

3 复杂度分析

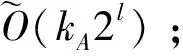
newtree算法每次运行的可以找到方案的概率为：

4 结 语

基于纠错码问题(规则字译码问题[11])设计的加密体制是目前抵抗量子计算机攻击的主要方案之一。本文提出的newtree算法，这种攻击算法可以对规则字译码问题进行攻击，其复杂度优于多碰撞算法的复杂度。

本文中我们给出了最近提出的多碰撞算法的一个改进算法newtree，主要思路体现在对积极列表和消极列表的处理方式上，从结果的公式比较可以得到渐进复杂度有所提高，但是newtree算法的局限性是它只适用于2

[1] Mosteller F. Understanding the Birthday Problem[J]. Mathematics Teacher, 1962, 55(5):322- 325.

[2] Wagner D. A Generalized Birthday Problem[M]//Advances in Cryptology—CRYPTO 2002. Springer Berlin Heidelberg, 2002:288- 304.

[4] Hoffstein J, Pipher J, Silverman J H. NTRU: A ring-based public key cryptosystem[M]//Algorithmic Number Theory. Springer Berlin Heidelberg, 1998:267- 288.

[5] Lyubashevsky V, Micciancio D, Peikert C, et al. SWIFFT: A Modest Proposal for FFT Hashing[M]//Fast Software Encryption. Springer Berlin Heidelberg, 2008:54- 72.

[6] Finiasz M, Gaborit P, Manuel S, et al.SHA-3 proposal: FSB. Submission to the SHA-3 NIST Competition (2008)[OL].http://www-rocq.inria.fr/secret/CBCrypto/index.php?pg=fsb.

[7] Meziani M, Özgür Dagdelen, Cayrel P L, et al. S-FSB: An Improved Variant of the FSB Hash Family[M]//Information Security and Assurance. Springer Berlin Heidelberg, 2011:132- 145.

[8] Overbeck R. A multiple birthday attack on NTRU[J]. IEEE Comput Graph Appl, 2011, 31(6):45- 55.

[9] Bernstein D J, Lange T, Niederhagen R, et al. Implementing Wagner’s generalized birthday attack against the SHA-3 round-1 candidate FSB[C]. Cryptosith Org, 2010, 2009.

[10] Coron J S, Joux A. Cryptanalysis of a Provably Secure Cryptographic Hash Function[C]//G Brassard Advances in Cryptology-Crypto Lncs, 2004:416- 427.

[11] Finiasz M, Gaborit P, Sendrier N. Improved Fast Syndrome Based Cryptographic Hash Functions[C]//Proceedings of ECRYPT Hash Workshop 2007.

[12] Suzuki K, Tonien D, Kurosawa K, et al. Birthday Paradox for Multi-collisions[C]//International Conference on Information Security and Cryptology. Springer, Berlin, Heidelberg, 2006:29- 40.