基于模糊RBF网络补偿的控制输入受限滑模控制
2018-07-04沈阳航天新光集团有限公司电源研究室李忠秋赵春雨
沈阳航天新光集团有限公司电源研究室 李忠秋 赵春雨 洪 洋 姜 波
1.引言
在实际系统中,执行器往往存在饱和现象,当控制饱和发生时,系统跟踪性能下降,该问题在某种程度上将影响控制系统的稳定性和控制性能,甚至使得整个控制系统不稳定。如何在控制输入限制的条件下实现有效的控制算法设计,是一个很有意义的命题,这就是“控制输入饱和”问题。
近年来针对执行器非线性受限情况的控制系统分析与综合问题受到广泛关注,并且近年来关于该类系统的滑模控制问题也开始受到许多研究者的关注,并取得了一些有意义的研究成果[1-4],然而,值得注意的是,已有的一些研究工作主要是针对线性控制系统,而由于非线性系统的复杂性,导致对于控制输入受限下非线性系统的滑模控制问题的研究工作尚不多见。
目前,处理饱和的方法有Nussbaum型函数法[5]、小增益控制法[6]、线性反馈调节法[7]、预测控制法[8]和指令滤波器法[9]等。然而, 文献[5-9]均是针对线性系统或仿射非线性系统,目前关于输入受限非线性系统控制的研究仍然较少。滑模控制(SMC)因其设计简单,控制精度高,且滑动模态对系统的摄动和外部扰动具有鲁棒性强等优势,已成为当前解决非线性问题的主要方法。但因控制输入存在符号函数,控制器抖振问题制约了传统滑模控制在工程中的应用。为了克服此弊端,文献[10]采用饱和函数代替符号函数,其代价是运动轨迹只能收敛到平衡点的某一邻域内;而模糊RBF神经网络能在一个紧凑集和任意精度下,逼近任何非线性函数,采用此网络可实现控制输入受限的有效补偿。
鉴于此,针对输入受限的实际工况控制系统,本文采用基于模糊RBF神经网络系统的滑模控制方法。具体而言,采用模糊系统与RBF神经网络相结合逼近输出受限值,通过滑模算法设计控制律,定义Lyapunuo函数并进行了相应的稳定性分析。数值仿真表明了本文控制方法的有效性和可行性。
2.系统描述
被控对象为:

其中为干扰为受限的控制量。取最大控制输入值为控制输入受限函数sat(v)表示为:

在实际工程中,若执行器幅值未知,会造成 δ 未知。通过设计模糊RBF网络,采用模糊RBF网络逼近 δ 的方法,可实现一种基于控制输入受限的滑模控制。闭环控制系统示意图如图所示。

图1 基于控制受限下的闭环控制系统Fig.1 Closed loop control system based on control constraints
3.基于模糊RBF网络的滑模控制器设计
3.1 RBF网络描述
RBF网络输入输出算法为:

其中,x为网络输入;i表示网络输入层第i个的输入;j为网络隐含层第j个网络输入为高斯基函数的输出;w为网络的理想权值;E为理想神经网络逼近 δ 的误差为网络输出为神经网络的估计权。
3.2 模糊系统描述
本文考虑具有单体模糊化、高斯隶属度函数、乘机推理和中心平均反模糊化的模糊系统。模糊系统的IF-THEN模糊规则描述如下:
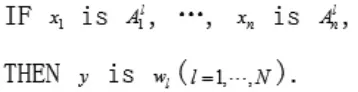
其中和y分别为模糊逻辑系统的输入和输出变量,模糊集,wl为第l条模糊规则中的单体值,N为逻辑规则数。将单个模糊规则集成后可以得到模糊系统如下:

定义模糊基函数:

这里令则模糊逻辑函数表示如下:

引理 1[11]令函数为定义在紧集上的一个连续函数,则对于,存在一个模糊逻辑系统使得:

最优估计参数:
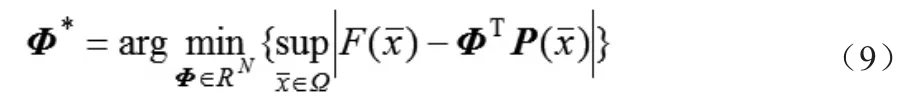
3.3 模糊RBF神经网络
模糊RBF神经网络结构图如图2所示,该网络由输入层、模糊化层、模糊推理层和输出层构成。
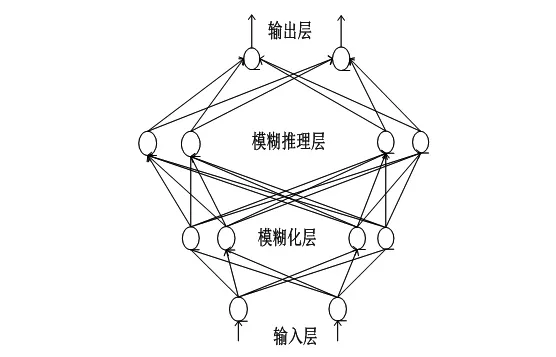
图2 模糊RBF神经网络结构图Fig.2 Fuzzy RBF neural network structure
第一层:输入层
该层的各个节点直接与输入量的各个分量连接,将压力、电流、速度作为模糊RBF网络的输入,对该层的每个节点i的输入输出表示为:

第二层:隶属函数层,即模糊化层。
该层的每个节点具有隶属函数的功能,采用高斯函数作为隶属函数。对第J个节点:
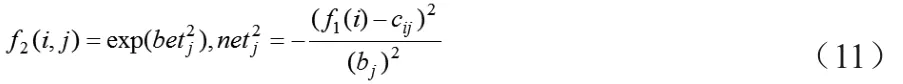
其中cij和bj分别是第i个输入变量的第j个模糊集合高斯函数的均值和标准差。
第三层:模糊推理层
该层通过与模糊化层的连接来完成模糊规则的匹配及各个节点之间的模糊运算。即通过各个模糊节点的组合得到相应的动态模糊强度。每个节点J 输出为该节点所有输入信号的乘积,即:

其中为输入层中第i个输入隶属函数的个数,即模糊化层节点数。
第四层:输出层
将电流效率、载流相对稳定系数、磨损率作为输出,该层的每个节点的输出为该节点所有输入信号的加权和,即:

其中L为输出层节点的个数,W为输出节点与第三层各节点的连接权矩阵。
3.3 控制器设计
网络输入取 x = v,则网络输出为
取则
取控制目标为为角度指令信号。定义角度误差为则滑模函数为则:

设计控制律为:

其中于是:

定义Lyapunov函数:其中

于是:
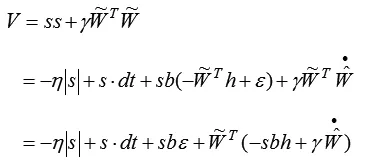
取自适应律为:

则由于当且仅当s = 0时则t →∞时,s →∞,且有界。神经网络只能逼近有界的函数,这就要求δ有界,本算法的稳定性取决于 δ 的有界性,即v的有界性。
4.仿真分析
Simulink主程序框图如图3所示,其中由控制子程序、神经网络逼近子程序和被控对象子程序构成。

图3 控制系统Simulink主程序框图Fig.3 Main program block diagram of control system Simulink
仿真系统仿真被控对象选取为:

?理想角度指令为为了表明控制系统补偿控制输入受限的能力,采用较大的初始误差。系统初始状态为[10,0]。RBF网络结构取1-5-1,网络输入取 x = v,根据网络输入实际范围来设计高斯基函数的参数,取和网络权值的初始值为0,采用控制律(15)和自适应律式(17),取滑模控制中,采用饱和函数代替切换函数,取边界层厚度Δ为0.02.仿真结果如图4~6所示。
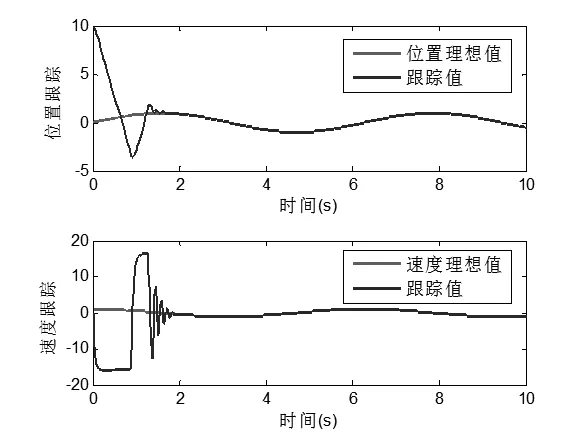
图4 位置和速度跟踪Fig.4 Position and velocity tracking curve

图5 受限前后控制输入v与uFig.5 Restricted front and rear control inputs v and u
由图4~6可知,本文设计的基于模糊RBF网络的滑模控制律能较好的保证系统状态的稳定。虽然由于状态时滞的影响, 在时间t = 1附近曲线轨迹有一个突变,但在t = 2时但本文所设计的滑模控制仍然很好地保证了状态轨迹的渐近稳定性。

图6 控制输入受限值δ及逼近Fig.6 Control input, restricted value δ and approximation
5.结论
本文应用滑模算法,针对实际输入受限的控制系统设计了基于模糊RBF网络补偿的自适应控制器,同时证明了闭环系统的跟踪性能。仿真结果表明,系统具有良好的跟踪性能,因此该方法具有较强鲁棒性和普适性,也可以推广运用于其他同类系统中。
[1]魏爱荣,赵克友.执行器饱和不确定线性系统的分析和设计[J].电机与控制学报,2005,9(5):448-451.
[2]陶洪峰,胡寿松.具有饱和死区非线性输入的自适应滑模跟踪控制[J].信息与控制,2009,38(3):281-285.
[3]Y.Niu and D.W.C.Ho.Design of sliding mode control for nonlinearstochastic systems subject to actuator nonlinearity 联[J].IEE Proc.-Control Theory Apply,2006,153(6):737-744.
[4]胡庆雷,马广富.带有输入非线性的挠性航天器姿态机动变结构控制[J].宇航学报,2006,27(4):630-634.
[5]Chen M,Zhou Y L,Guo W W.Robust tracking controlfor uncertain MIMO nonlinear system with input saturationusing RWNNDO[J].Neuroco mputing,2014,144(20):436-447.
[6]Gronardf F,Sepulchre R,Bastin G.Improving the performance of low-gain designs for bounded control of linear systems[J].Automatica,2002,38(10):1777-1782.
[7]Chaouif Z,Giri F,Saad M.Asymptotic stabilization of linear plants in the presence of input and output saturations[J].Automatica,2001,37(1):37-42.
[8]Grune L,Pannek J.Nonlinear model predictive control[M].London: Springer-Verlag,2011:89-96.
[9]Farrell J A,Polycarpou M,Sharma M,et al.Command filtered backsteopping[J].IEEE Trans on Automatic Control,2009,54(6):1391-1395.
[10]Khalil H K.Nonlinear systems[M].New Jersey:Prentice Hall,2002:566-572.
[11]王立新.自适应模糊系统与控制-设计与稳定性分析[M].北京:国防工业出版社,1995.
