TMAu5(TM=Y-Cd)团簇稳定结构与电磁特性的第一性原理

陈朝华， 刘 凯， 谢 尊

(1. 石家庄理工职业学院 通识教育学院， 河北 石家庄 050228；2. 河北师范大学 物理科学与信息工程学院新型薄膜材料重点实验室， 河北 石家庄 050024)

在过去的十多年里，众多研究人员从事关于二元过渡金属(TM)团簇的研究[1-6].大量的理论和实验研究表明，掺杂原子可以明显改变主团簇的物理和化学特性[7-10].由于其在纳米技术、微电子和材料科学等方面的潜在应用，设计出具有良好电子结构和磁特性的TM掺杂金团簇便成为了研究人员不懈的追求.例如，文献[11]通过理论计算得出TM掺杂的Au团簇与3p杂质原子(Al,Si,P,S,Cl)掺杂的Au团簇展现出了不同的生长模式、结构稳定性以及电磁特征.通过运用从头计算方法，文献[12]系统研究了GdAun，发现幻数团簇Gd@Au15具有较高的磁矩，它的最高占据分子轨道(HOMO)与最低未占据分子轨道(LUMO)之间的能隙(HOMO-LUMO gap)也较大.文献[13]报道M@Au24(M=V,Cr,Mn,Fe,Co,Ni)的红外光谱相比Au24已经发生了改变.由于独特的物理化学特征，理论上对XAu5也进行了广泛研究.在文献[14]中提到，MgAu5和SAu5的基态为平面三角结构，而AlAu5、SiAu5和PAu5最稳结构更倾向于三维立体结构.阳离子Au5M+(M=Sc,Ti,V,Cr,Mn,Fe)团簇的正电荷主要集中在M原子上，且正电荷数随团簇尺寸的增大而减小[15].此外，二元合金团簇也表现出不同的表面效应和尺寸效应，这一点不同于块体材料.在本文中，应用密度泛函理论，详细计算了4d TM掺杂的TMAu5(TM=Y-Cd)团簇的几何结构、电子结构和磁特性，希望本文的计算结果能够提供一些掺杂原子对于主团簇影响的详细信息，同时也能在新材料设计方面提供一些理论参考.

1 理论方法

基于密度泛函理论，采用广义梯度近似(GGA)下的交换关联函数PW91[16]和DNP[17]基组设置.考虑到Y等重元素的相对论效应，也为了减少计算量，采用包含标量相对论效应的有效核势(ECP)[18-20].为了得到全局最小化，对于每个TMAu5，优化了不少于20个初始结构位型.对于偶数电子的TMAu5(TM=Y,Nb,Tc,Rh,Ag)，要考虑自旋多重度sM=1,3,5,7，…;对于奇数电子的TMAu5(TM=Zr,Mo,Ru,Pd,Cd)，要考虑自旋多重度sM=2,4,6,8，….自洽场迭代计算的收敛标准设置如下：力和原子位移分别收敛到小于1×10-2Hartree/nm和1×10-4nm,电荷密度收敛到1×10-3e/nm3，对应总能收敛到10-6Hartree.对于优化后得到的结构，通过计算振动频率来验证其存在的可能性.若出现虚频，则对虚频结构进行点群调整,再采取相同的方法重新进行结构优化，直到虚频消失为止，从而最终确定基态结构.电荷转移和自旋磁矩的计算在Mülliken布局分析下实现[21].在几何优化中不限制任何对称性，所有计算均采用量子化学软件包Dmol3[17,22]来完成.

2 结果与讨论

为了获得基态结构，在GGA/PW91/DNP水平下优化了一系列TMAu5团簇的各种可能的初始结构位型，如图1所示，几何优化后获得的最稳态结构如图2所示，并在表1中列出了TMAu5基态的相关参数.首先对Au6的可能结构进行了计算，得到的基态为等边三角形结构，点群对称性为D3h，也显示在图2中，这与以前的理论计算结果[23]一致.

灰球和黑球分别代表Au和TM原子

图 2 Au6和TMAu5(TM=Y-Cd)团簇的基态结构

团簇结构的对称性自旋多重度平均结合能/eV能隙/eV总磁矩/μB局域磁矩/μB电荷/e振动频率/cm-1YAu5Cs12.0281.48100.0001.754221.1ZrAu5C122.2050.35610.3171.462252.6NbAu5C112.3401.16900.0001.287269.6MoAu5C2v41.5110.45033.2371.005228.0TcAu5C2v52.1941.07343.9060.753244.1RuAu5C2v42.0430.61732.8280.590234.5RhAu5C2v31.7260.97121.8270.371205.0PdAu5C2v21.7440.46210.7340.292191.0AgAu5C2v11.8642.19600.0000.322188.0CdAu5C2v21.4330.38810.4460.399195.5

TMAu5优化结果显示，TMAu5(TM=Y-Nb)的基态结构为三维立体结构，TM原子占据与Au形成配位数为5的位置；而其余TMAu5(TM=Mo-Cd)的基态结构为平面结构，点群对称性都是C2v，其中TMAu5(TM=Mo-Ru)的基态结构是类蝴蝶状结构，TM占据与Au形成配位数为5的位置;而TMAu5(TM=Rh-Cd)的基态结构是类似于Au6基态的三角形结构，TM占据与Au形成配位数为4的位置.非常明显，所有TMAu5的最稳态结构中，TM原子往往占据与Au原子形成较大配位数的位置，这与分子轨道理论中轨道的最大重叠原则是一致的.对于具有相似结构的TMAu5异构体，平均结合能随着TM原子配位数的增大而降低.

我们研究了TMAu5(TM=Y-Cd)基态结构的平均结合能，并和Au6进行了对比.TMAu5和Au6的平均结合能定义如下：

(2)

其中，E(Au)、E(TM)、E(TMAu5)和E(Au6)分别代表Au原子、TM原子、TMAu5团簇和Au6团簇的总能.TMAu5和Au6基态结构的平均结合能如图3所示.可以看出,TMAu5(TM=Y,Zr,Nb,Tc,Ru,Ag)的平均结合能大于Au6的平均结合能，而TMAu5(TM=Mo,Rh,Pd,Cd)的平均结合能则小于Au6的平均结合能.换而言之，用一个4d TM(TM=Y,Zr,Nb,Tc,Ru,Ag)取代Au6的一个Au原子增加了主团簇的相对稳定性.其中，NbAu5的平均结合能最大，说明它的稳定性也是最高的.此外，CdAu5的平均结合能在所有TMAu5中是最小的，这可能是由于Cd原子的4d壳层和5s壳层都是闭壳层，而其他的TM原子的4d壳层或5s壳层是开壳层的缘故.

图 3 TMAu5(TM=Y-Cd)和Au6团簇基态结构的平均结合能

从电子跃迁的角度来说，HOMO-LUMO gap(Gap)是反映电子从HOMO跃迁到LUMO能力的重要参数，在一定程度上代表了团簇参与化学反应的能力.团簇的Gap越大，说明团簇的化学稳定性越高.为了研究二元合金团簇的化学稳定性和成键特性，计算了TMAu5团簇的Gap，如图4所示.计算得到的Au6基态的Gap为2.174 eV，这与文献[24]计算的结果(2.17 eV)非常接近.从图4可以看出，TMAu5团簇的Gap表现出明显的奇偶振荡行为，AgAu5的Gap稍微高于Au6的Gap，说明AgAu5的化学稳定性是最高的，可以作为块体组装材料的基本单元；其他的TMAu5团簇的Gap值明显低于Au6的Gap值，说明它们具有较高的化学活性.

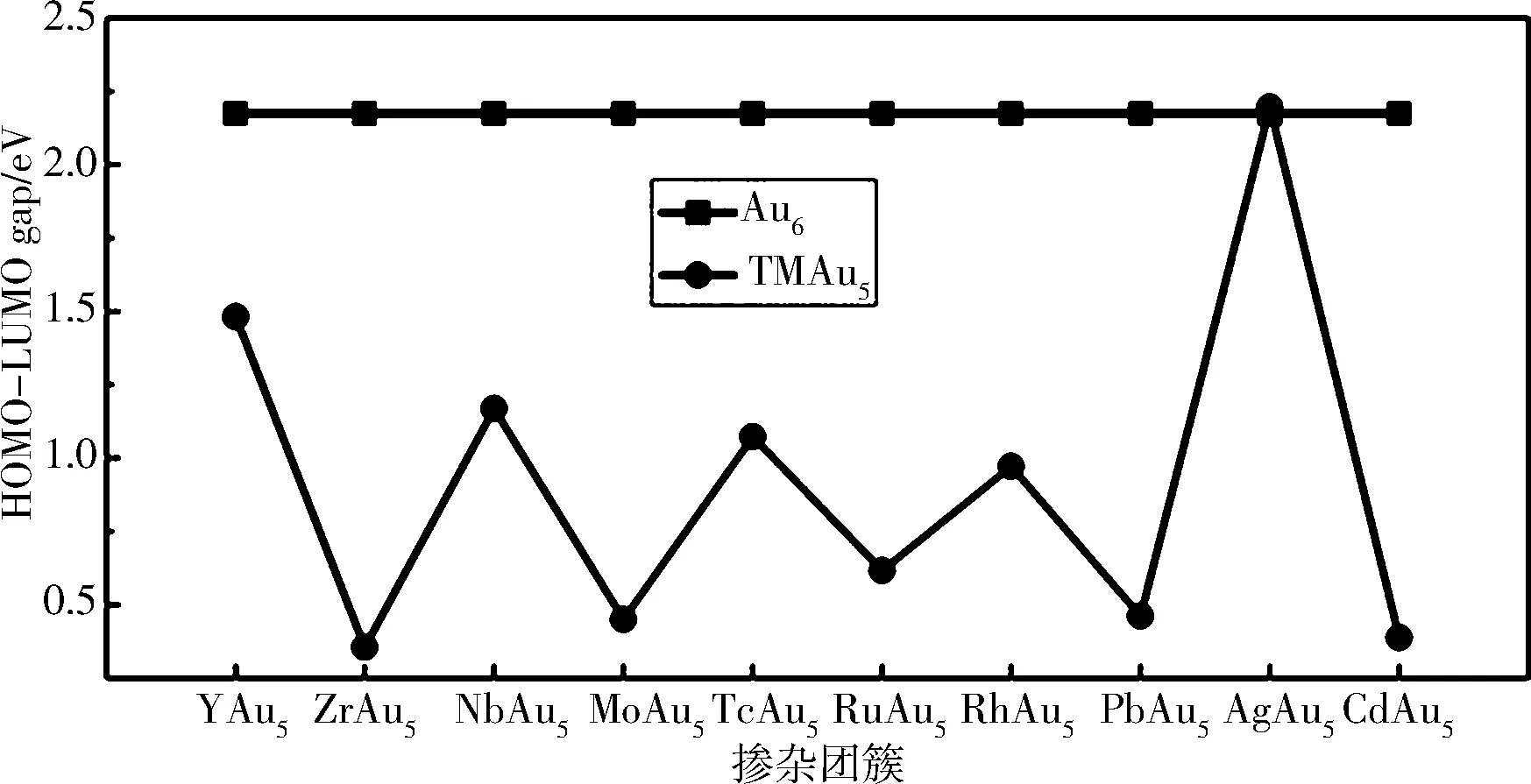
图 4 TMAu5(TM=Y-Cd)和Au6团簇基态结构的能隙

图 5 TMAu5(TM=Y-Cd)基态结构的总磁矩和TM原子的局域磁矩

基于原子团簇的尺寸、结构和成分易于调控，团簇可以作为探究物质磁特性的理想媒介.结合表1、表2和图5可以看出，TMAu5团簇的总磁矩在0～4 μB之间变化.TMAu5(TM=Y,Nb,Ag)的总磁矩和TM原子磁矩发生湮灭现象，而TcAu5的磁矩为最大值4 μB.TMAu5(TM=Mo-Pd)的总磁矩与TM原子的磁矩比较接近，这说明TMAu5(TM=Mo-Pd)的总磁矩主要由TM原子的磁矩决定，其余Au原子的磁矩对总磁矩的影响较小.同时，TM的磁矩主要来自于TM中4d电子的磁矩，而5s和5p电子对TM的磁矩贡献较小.我们也注意到，TMAu5(TM=Zr,Cd)的总磁矩均为1 μB，主要来自于TM和Au的磁矩.对于MoAu5，Mo原子磁矩大于MoAu5的总磁矩，表明Mo的磁矩与其余Au的磁矩表现出反铁磁性耦合；对于TMAu5(TM=Zr,Tc-Pd,Cd)，TM的磁矩小于总磁矩，表明TM的磁矩与其余Au的磁矩表现出铁磁性耦合.通过Mülliken布局分析，得出所有TM原子均带正电荷，表明TM原子丢失电子，而Au原子得到电子，即TM原子作为电子的施主，而Au原子则作为电子的受主.同时，我们也计算了TMAu5中TM原子的4p、4d、5s和5p轨道上的电荷与磁矩，汇总在表2.对比自由TM原子的价电子组态，可以得出大多数TM原子的4d和5s轨道均丢失一定数量的电子，而5p轨道获得一定数量的电子，说明4d和5s轨道上的电子转移到了5p轨道上，以及TM原子中存在着spd杂化.进一步分析发现,TM原子的4d和5s轨道丢失电子数大于5p轨道获得电子数，例如,RuAu5中Ru的电子态为4d6.6695s0.5435p0.208，而自由Ru的电子态为4d75s1，4d和5s轨道丢失0.788 e，空5p轨道得到0.208 e，说明Ru的4d和5s轨道除了向自身5p轨道转移电子外，必定还有多余的一部分电子转移到了Au原子上.而通过RuAu5中Au的电子组态和自由Au原子的电子组态对比分析，发现Au的5d轨道丢失的电子数小于6s和6p轨道得到的电子数，说明Au的6s和6p轨道得到的电子除了来自自身的5d轨道外，必定还有一部分电子是来自于Ru原子的4d和5s轨道，说明Au原子中也存在着spd杂化.这与上述关于电荷转移方由TM转向Au的分析是一致的，反映出TM原子与Au原子之间也存在着杂化现象.

表 2 TMAu5基态团簇中TM原子的4p，4d，5s和5p态的电荷与磁矩

为了更好地理解TMAu5磁矩的变化机制，计算了s、p、d各态的分波态密度(PDOS)以及TM的局域态密度(LDOS).以AgAu5和TcAu5为例，如图6所示.在费米能级附近，AgAu5和TcAu5的PDOS主要来自于d态，其次是s态，而p态对整体的贡献较小，反映了明显的spd杂化现象.在AgAu5的PDOS中，自旋向上的DOS和自旋向下的DOS非常对称，未发生自旋劈裂现象，表明AgAu5的总磁矩为0 μB.而TcAu5的自旋向上的DOS和自旋向下的DOS并不对称，产生了非零磁矩(4 μB).通过对TcAu5中Tc的LDOS分析，Tc磁矩主要来自于4d电子，而5s和5p态对Tc磁矩的贡献较小，这与以上分析一致.综上所述，TMAu5磁矩的变化可能是由于电荷转移和轨道杂化造成的.

图 6 AgAu5和TcAu5基态结构的分波态密度和Tc原子的局域态密度

此外，我们也计算了TMAu5的HOMO、LUMO和差分电荷密度(DED)，如图7所示.可以看出，对于HOMO和LUMO，电子云主要围绕在TM原子周围，而在Au原子上也有一定量的电荷密度分布.TM和Au原子周围的轨道形状表现出明显的d轨道特征，TM的HOMO和LUMO主要表现出类dz2轨道，而Au的HOMO和LUMO表现出类dz2轨道和类d(dxy,dxz,dyz,dx2-y2)轨道，TM-Au和Au-Au原子之间的spd杂化影响着TMAu5几何结构与稳定性.从图7中可以看出，成键电子主要聚集在TM-Au之间和Au-Au之间，而在TM和Au周围出现少量的电子聚集区域和大量的电子损耗区域，这显示出明显的共价键和离子键的特征，电子成键结构也决定着团簇的几何结构.通过对比Au6与AgAu5的DED，发现一个Ag原子取代一个Au原子后，Ag-Au之间的电子聚集相比较Au6中Au-Au之间电子聚集出现了明显地增加，进一步证明Ag-Au之间的相互作用强于Au-Au之间的相互作用，也体现了AgAu5的稳定性高于Au6团簇.

图 7 TMAu5(TM=Y,Ru,Rh,Pd)基态的HOMO和LUMO图与TMAu5(TM=Y,Tc,Ag)和Au6基态的差分电荷密度

3 结论

应用第一性原理，系统研究了TMAu5(TM=Y-Cd)团簇的基态结构和电磁特性.计算结果显示TMAu5(TM=Y-Nb)的基态结构为立体结构，而TMAu5(TM=Mo-Cd)的最稳定结构是平面结构，TM往往位于与Au形成较大配位数的位置.通过对比TMAu5与Au6平均结合能和能隙，发现TM(TM=Y,Zr,Nb,Tc,Ru,Ag)原子明显地加强主团簇的稳定性，同时也发现AgAu5的化学稳定性较高，而TMAu5(TM=Y-Pd,Cd)的化学活性较强.通过对电磁特性分析显示电子总是从TM原子转到Au原子上，TMAu5(TM=Mo-Pd)的总磁矩主要由TM原子磁矩提供，而TM原子的磁矩主要来源于TM的4d电子的磁矩.希冀本文的结果使TMAu5可能应用在设计可调制磁矩的新材料中.

[1] HAN S L, XUE X, NIE X C, et al. First-principles calculations on the role of Ni doping in Cunclusters:from geometric and electronic structures to chemical activities towards CO2[J]. Phys Lett,2010,A374(42):4324-4330.

[2] ZHOU Y H, ZENG Z, JU X. The structural and electronic properties of CumAgn(m+n=6) clusters[J]. Microelectron J,2009,40(4): 832-834.

[3] CHENG X H, DING D J, YU Y G, et al. Geometrical structures and electronic properties of copper-doped aluminum clusters[J]. Chin J Chem Phys,2012,25(2):169-176.

[4] SU W, QIAN P, LIU Y, et al. First principle calculations of Yttrium-doped palladium clusters[J]. Comput Phys Commun,2010,181(4):726-731.

[5] CHENG D, HUANG S, WANG W. The structure of 55-atom Cu-Au bimetallic clusters:monte carlo study[J]. Eur Phys J D,2006,39(1):41-48.

[6] VENKATARAMANAN N S, SAHARA R, MIZUSEKI H, et al. Titanium-doped nickel clusters TiNin(n=1～12):geometry, electronic, magnetic, and hydrogen adsorption properties[J]. J Phys Chem,2010,A114(15):5049-5057.

[7] OHARA M, MIYAJIMA K, PRAMANN A, et al. Geometric and electronic structures of terbium-silicon mixed clusters (TbSin; 6 ≤n≤ 16)[J]. J Phys Chem A,2002,106(15):3702-3705.

[8] LI Y F, KUANG X Y, WANG H Q. Probing the structural and electronic properties of lanthanide-metal-doped silicon clusters:M@Si6(M=Pr, Gd, Ho)[J]. Phys Lett,2011,A375(30/31):2836-2844.

[9] HENRY G R, REVELES J U, SANDOVAL Z G. High magnetic moments on binary Yttrium-alkali superatoms[J]. Chem Phys Lett,2013,583(1):97-102.

[11] ZHANG M, YANG S B, FENG X J, et al. Structural stability and electronic properties of small gold clusters induced by 3p electron atoms[J]. Eur Phys J D,2013,67(1):11.

[12] YADAV B D, KUMAR V. Gd@Au15:a magic magnetic gold cluster for cancer therapy and bioimaging[J]. Appl Phys Lett,2010,97(13):133701.

[13] YANG A, FA W, DONG J. Magnetic properties of transition metal-doped tubular gold clusters:M@Au24(M = V, Cr, Mn, Fe, Co, and Ni)[J]. J Phys Chem,2010,A114(12):4031-4035.

[14] MAJUMDER C, KANDALAM A K, JENA P. Structure and bonding of Au5M (M=Na, Mg, Al, Si, P, and S) clusters[J]. Phys Rev,2006,B74(20):3840-3845.

[15] TORRES M B, FERNANDZE E M, BALBAS L C. Theoretical study of structural, electronic, and magnetic properties of AunM+clusters (M=Sc, Ti, V, Cr, Mn, Fe, Au;n≤ 9)[J]. Phys Rev B,2005,71(15):155412.

[16] PERDEW J P, CHEVARY J A, VOSKO S H, et al. Atoms, molecules, solids, and surfaces:applications of the generalized gradient approximation for exchange and correlation[J]. Phys Rev,1992,B46(11):6671-6687.

[17] DELLEY B. An all-electron numerical method for solving the local density functional for polyatomic molecules[J]. J Chem Phys,1990,92(1):508-517.

[18] STEVENS W J, KRAUSS M, BASCH H. Compact effective potentials and efficient shared-exponent basis sets for the first-and second-row atoms[J]. J Chem Phys,1984,81(12):6026-6033.

[19] STEVENS W J, BASCH H, KRAUSS M, et al. Relativistic compact effective potentials and efficient, shared-exponent basis sets for the third-, fourth-, and fifth-row atoms[J]. Can J Chem,1992,70(2):612-630.

[20] CUNDARI T R, STEVENS W J. Effective core potential methods for the lanthanides[J]. J Chem Phys,1993,98(7):5555-5565.

[21] MULLIKEN R S. Electronic population analysis on LCAO-MO molecular wave functions. II. Overlap populations, bond orders, and covalent bond energies[J]. J Chem Phys,1955,23(10):1841-1846.

[22] DELLEY B. From molecules to solids with the DMol3approach[J]. J Chem Phys,2000,113(18):7756-7764.

[23] LI X B, WANG H Y, YANG X D, et al. Size dependence of the structures and energetic and electronic properties of gold clusters[J]. J Chem Phys,2007,126(8):084505.

[24] TAFOUGHALT M A, SAMAH M. Density functional investigation of structural and electronic properties of small bimetallic silver-gold clusters[J]. Physica,2012,B407(12):2014-2024.