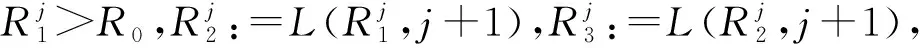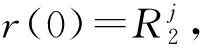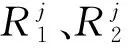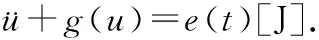一类双质子耦合格点系统的对称周期解

王 超, 黄娟娟, 杨 潇

(盐城师范学院 数学与统计学院, 江苏 盐城 224001)

1 引言及预备知识

本文考虑双质子耦合格点系统

(1)

其中h、p是连续的2π-周期偶函数且满足

权函数q(t):R→R+为2π-周期连续函数,g:R→R是局部Lipschitz连续函数且满足

一维质子链系统具有广泛的应用背景.例如,对于系统(1),当q(t)≡A∈R,g:R+→R+在原点具有奇性时,系统(1)可以刻划在一条直线上的2个受迫充电质子的运动[1].在文献[1]中,Torres等讨论了周期解存在的充分必要条件,他们通过使用变量代换的方法对系统进行降维后得到文献[1]中的结果,并在文献[2-3]中把结果推广到无限维的情形.另外,在文献[2-3]中对Toda链的情形也进行了讨论.关于一维质子链系统的研究有许多工作,涉及到解的动力行为的许多特征,如周期解[4-5]、拟周期解的不变环面[6]、离散孤立子和呼吸子[7]、同宿行波解的存在性[8]以及指数吸引子[9]等,其中,文献[4，6-7]涉及到时变的FPU链.

定义1.1函数(x(t),y(t))称为方程(1)偶的2kπ-周期解(k∈Z+),如果对正整数k有

(x(0),y(0))=(x(2kπ),y(2kπ)),(x′(0),y′(0))=(x′(2kπ),y′(2kπ)),

且对任意t∈[0,2kπ]都有

(x(-t),y(-t))=(x(t),y(t)).

特别地,当k=1时,称(x(t),y(t))为方程(1)偶的调和解;当k>1时,称(x(t),y(t))为方程(1)偶的次调和解.

关于方程对称周期解的讨论也是动力系统的一个有趣问题,它与方程的稳定性问题有关.一个经典的工作是Nakajima在文献[10]中证明了Duffing方程无穷多个对称调和解的存在性以及对称次调和解的稠密性分布结果.在文献[1]中,作者考虑二阶方程

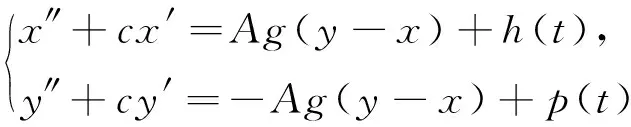
(2)

的周期解问题时,主要的证明方法还是降维.通过讨论降维后2个非耦合方程周期解的存在性来推断原来系统周期解的存在性问题;但当方程是偶对称方程时,证明方程是否存在偶的周期解并不是一件容易的事.事实上,对降维后的等价方程而言,即使能够证明其中一个方程具有偶的周期解,也不能轻易看出另一个非耦合方程也具有偶的周期解.

针对上述主要困难,本文在引理1.1中解决了这一问题.我们证明:对于降维后的等价方程组,只要其中一个非耦合方程具有偶的周期解,则原系统一定存在与之对应的偶的周期解.

令

为二阶自治方程x″+g(x)=0的轨道

上的周期解的最小正周期,其中

且e为充分大的正实数.记

其中,h>0为充分大的正实数.本文将考虑下述2种情况时,方程(1)的对称周期解问题:

当考虑条件(τ1)的情况时,为了满足解的可延拓性,要求权函数q(t):R→R+为连续的有界变差函数,且满足:

(q0) 1) ∀t∈[0,2π],q(t)≥0,且{t∈[0,ω]:q(t)>0}≠Ø;

2) 集合{t∈[0,2π]:q(t)≡0}只有有限个连通分支;

3) 若在(c,d)⊂[0,2π]上q>0且q(c)=0(或q(d)=0),则q在c的一个右邻域内单调不减(或相应地q在d的一个左邻域内单调不增).

本文首先给出了证明方程(1)存在偶的周期解的一般性框架与偶的周期解存在的充分必要条件;其次,针对超线性条件(τ1),证明了方程(1)无穷多个偶的调和解的存在性;最后,针对次线性条件(τ2),证明了方程(1)无穷多个偶的次调和解的存在性.

2 引理

类似于文献[3]中的做法,作变量代换

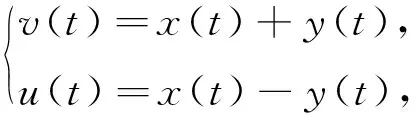
(3)

得方程(1)的等价系统

v″=h(t)+p(t),

(4)

u″+2q(t)g(u)=p(t)-h(t).

(5)

下面,分别研究方程(5)的偶周期解的存在性和重性问题.事实上,若方程(5)存在偶周期解u(t)且方程(4)存在偶周期解v(t),则易见

是方程(1)的偶的周期解.

下面,研究方程(1)存在偶周期解的条件.

引理2.1设(h0)成立,则方程(4)一定存在周期为2π的偶周期解.

证明设函数F(t)是h(t)+p(t)的一个原函数,令

φ(t)=F(t)-F(0),

则显然有φ′(t)=h(t)+p(t)且φ(0)=0.

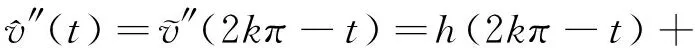
p(2kπ-t)=h(t)+p(t),

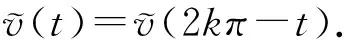
注意到

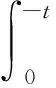
得

v′(-t)=-v′(t),

即

φ(-t)=-φ(t).

从而有

v′(-π)=-v′(π).

因为

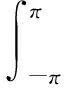
由(h0)知

v′(π)-v′(-π)=2v′(π)=0,

从而

v′(π)=v′(0)=0.

根据上述命题知

v(t)=v(-t)=v(t+2π).

得证.

推论2.1若方程(5)存在偶的调和解,则方程(1)一定存在偶的调和解(x(t),y(t)).

称一个偶的周期解u(t)的初值点(u(0),u′(0))为一个ε-点,由u的偶性可知u′(0)=0.特别地,若一个偶的周期解u(t)的最小周期为2mπ(m∈Z+),称ε-点(u(0),u′(0))为m阶的.

引理2.2[11]方程(5)的一个解u(t)是一个偶的周期解当且仅当存在一个正整数m,使u′(0)=u′(mπ)=0.特别地,这个ε-点(u(0),u′(0))为m阶的当且仅当u′(0)=u′(mπ)=0且u′(kπ)≠0,k=1,2，…,m-1.

设对二维欧式空间R2中的每一个点q=(a,b)∈R2,定义

记u(t,a)为方程(5)在t=0时刻从(a,0)出发的解,a∈R.从引理2.1可知(a,0)是一个ε-点当且仅当存在某一个正整数m≥1使

u′(mπ)=0.

(6)

3 问题的转化

考虑方程(5)的等价系统

(7)

其中，g1(u)=2g(u),e(t)=p(t)-h(t).

设连续截断函数η:R2→R为

且满足|η(u,w)|≤1.定义新的系统

(8)

在原点附近系统(8)为

u′=w,w′=-q(t)g1(u).

容易看出此时原点为该系统的平衡点,由解的唯一性可知从原点外任一点出发的解都不会经过原点.在半径为1的圆域之外,系统(8)为

u′=w,w′=-q(t)g1(u)+e(t).

显然此时与原系统(7)一样,从而系统(8)的任一满足|(u(t),w(t))|>1的解都是原系统(7)的解.

设(u(t;u0,w0),w(t;u0,w0))为方程(8)满足初值(u(0),w(0))=(u0,w0)的连续解.

引进极坐标:假设(u0,w0)≠(0,0),则解(u(t;u0,w0),w(t;u0,w0))可以用极坐标表示

(9)

其中r(t)、θ(t)是连续函数.易证,在坐标变换(9)下,(r(t;r0,θ0),θ(t;r0,θ0))满足方程

其中,u0=r0cosθ0,w0=r0sinθ0.

在下文中,为了讨论方便,总假设对∀R>R0,记(r(t,R),θ(t,R))为方程(10)的满足r(0)=R,θ(0)=0(modπ)的解.

由u(t,a)的定义和方程(9)知,θ(t,a)是t的连续函数且可设θ(0,a)=0(因为u′(0,a)=0).从方程(6)可知下述引理成立.

引理3.1(a,0)是一个ε-点,即u(t,a)是一个偶的周期解当且仅当存在某个m≥1使得

θ(mπ,a)=0(modπ).

(11)

定义

为向量(u(t),w(t))在区间[t1,t2]上随时间增加时在相平面上所转的角度增量.易见,该值与θ(t)的选择无关.因此,方程(11)也可以表示为

θ(mπ,a)-θ(0,a)=lπ,l∈Z.

(12)

4 超线性方程

假设权函数q(t):R→R+为2π-周期连续的有界变差函数且满足条件(q0).

类似于文献[12]中的方法,可以证明下面的引理.

引理4.1假设(g0)和(q0)成立,任取(u0,w0)∈R2,则解(u(t;u0,w0),w(t;u0,w0))在(-∞,+∞)上有定义.

推论4.1对任一个L>0和α>0都存在一个常数β(α,L)>0,使

1) 若|(u0,w0)|≤α,则|(u(t),w(t))|≤β(α,L),对|t|≤L;

2) 若|(u0,w0)|>β(α,L),则|(u(t),w(t))|>α,对|t|≤L.

易证存在充分大的正数R*>0使得对任意的a>R*以及t∈(0,π],有θ(t,a)<0.

引理4.2[11]假设(g0)、(τ1)和(q0)成立,则对任意的正数H>0,都存在一个正数R=R(H)>R*,使得如果(r(t),θ(t))为方程(10)的定义在[a,b]上的一个解且满足r(a)≥R,则有

θ(a)-θ(b)≥2πH.

引理4.3假设(g0)、(τ1)和(q0)成立,则方程(5)有无穷个偶的2π-周期解.

证明将证明分成以下两步:第一步,从有关方程(11)的讨论可知,我们的目标是找到一列数{ak},使得当k→±∞时有ak→±∞且θ(π,ak)=0(modπ).因为对于充分大的β>0来说,集合{θ(π,α);α>β}和{θ(π,α);α<-β}是连续的,所以,相应地,只须证明

(13)

第二步，定义

表示从点(0,a)出发的解在区间[0,π]内绕原点旋转的圈数,记

x(t,a)=x(t;0,(a,0)),

x′(t,a)=x′(t;0,(a,0)),

易见

rot[0,π](a):=

注意到e(t)是有界函数,由推论4.1和引理4.2可得:当|a|→+∞时,对任意的t∈[0,π]都有

r(t,a)→+∞,

且

rot[0,π](a)→+∞.

注4.1对充分大的β>0,若定义函数

Φ:[β,+∞)→R

则易证存在正数γ使得函数的值域为

Φ([β,+∞)):=(-∞,-γ].

由引理3.1和(12)式知,存在可数个al∈[β,+∞)满足

θ(π,a)-θ(0,a)=lπ,l∈Z,

因此方程(5)有可数个偶的2π-周期解.

由引理4.3、引理2.1和推论2.1有定理4.1.

定理4.1假设(g0)、(τ1)和(q0)成立,则方程(1)有无穷多个偶的2π-周期解.

5 次线性方程

假设函数g(x):R→R满足(g0)和(τ2).

引理5.1[13]存在正数R0>1,对(10)式的任意解(r(t),θ(t)),若r(t)>R0,则θ′(t)<0.

类似于文献[14]中的方法,容易证明下述引理.

引理5.2假设(g0)和(τ2)成立,若(r(t),θ(t))是方程(10)的解满足

r(t)≥R1≥R0, 0

和

θ(t2)-θ(t1)=-2π,

则

引理5.3[13]对每一个R>R0和每一个j>0,都存在L(R,j)>R使得如果(r(t),θ(t))是方程(10)的解满足r(t1)=L(R,j),r(t2)=R(或者r(t1)=R,r(t2)=L(R,j))及

R≤r(t)≤L(R,j), ∀t∈[t1,t2],

则

θ(t2)-θ(t1)<-2jπ.

另一方面,由θ′的连续性易证下述引理.

引理5.4设R2>R1>R0是充分大的正数,(r(t),θ(t))是(10)式的一个解满足

R1≤r(t)≤R2, ∀t≥0,

则

θ(t)-θ(0)→-∞,t→+∞.

定理5.1假设(g0)、(τ2),则方程(5)有无穷个偶的次调和解.

θ(mπ)-θ(0)<-2jπ.

1) 或者(u(t),v(t))∈Aj,∀t∈[0,mπ],其中(u(t),v(t))由(9)式给出;

θ(mπ)-θ(0)<-2jπ.

以及

[1] TORRES P J, ZANOLIN F. Periodic motion of a system of two or there charged particles[J]. J Math Anal Appl,2000,250(2):375-386.

[2] TORRES P J. Periodic motions forced infinite lattices with nearest neighbor interaction[J]. Z Angew Math Phys,2000,51(3):333-345.

[3] TORRES P J. Necessary and sufficient conditions for existences of periodic motions of forced systems of particles[J]. Z Angew Math Phys,2001,52(3):535-540.

[4] SUN J, MA S. Nontrivial periodic motions for resonant type asymptotically linear lattice dynamical systems[J]. J Math Anal Appl,2014,417(2):622-634.

[5] WANG C, QIAN D. Periodic motions of a class of forced infinite lattices with nearest neighbor interaction[J]. J Math Anal Appl,2008,340(1):44-52.

[7] GENDELMAN O. Exact solutions for discrete breathers in a forced-damped chain[J]. Physical Review E:Statistical Nonlinear & Soft Matter Physics,2013,87(6):062911.

[8] LIU Z, GUO S, ZHANG Z. Existence of homoclinic travelling waves in infinite lattices[J]. Bulletin of the Malaysian Mathematicalences Society,2013,36(4):965-983.

[9] ZHOU S F, HAN X Y. Pullback exponential attractors for non-autonomous lattice systems[J]. J Dynamics and Differential Equations,2012,24(3):601-631.

[11] 王超. 一类带正权超线性对称方程对称周期解的分布[J]. 四川师范大学学报(自然科学版),2011,34(6):844-849.

[12] PAPINI D. Boundary value problems for second order differential equations with superlinear terms:a topological approach[D]. Trrieste:Scuola Internazionale Superiore di Studi Avanzati,2000.

[13] 杨潇,周鑫,杨晓燕,等. 一类次线性双质子耦合格点系统的周期解[J]. 四川师范大学学报(自然科学版),2016,39(2):236-241.

[14] DING T, ZANOLIN F. Subharmonic solution of second order nonlinear equations:a time-map approach[J]. Nonlinear Analysis Theory Methods & Applications,1993,20(5):509-532.

[15] FABRY C, HABETS P. Periodic solutions of second order differential equations with superlinear asymmetric nonlinearities[J]. Arch Math,1993,60(3):266-276.

[16] PAPINI D, ZANOLIN F. Differential equations with indefinite weight:boundary value problems and qualitative problems of the solutions[J]. Rendiconti Del Seminario Matematico,2003,60(4):265-295.