包含Chebyshev多项式的r-循环矩阵的谱范数
2018-07-04师白娟
师白娟
(西北大学 数学学院, 陕西 西安 710127)
1 引言及预备知识
对任意n≥0,著名的第一、二类切比雪夫多项式Tn(x)和Un(x)的定义如下:
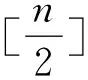
显然Tn(x)和Un(x)是二阶线性递推多项式,并且满足递推公式:
Tn+1(x)=2xTn(x)-Tn-1(x),n≥1,
T0(x)=1,T1(x)=x,
T2(x)=2x2-1,T3(x)=4x3-3x;
Un+1(x)=2xUn(x)-Un-1(x),n≥1,
U0(x)=1,U1(x)=2x,
U2(x)=4x2-1,U3(x)=8x3-4x.
{Tn(x)}和{Un(x)}的通项公式为:
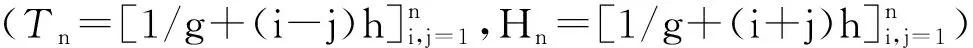
受上述文献的启发,研究包含第一类Chebyshev多项式和第二类Chebyshev多项式的r-循环矩阵的谱范数和Euclidean范数.
定义1.1矩阵A=(aij)∈Mm×n的欧几里得范数与谱范数定义为:
其中,λi是矩阵AHA的特征值,矩阵AH是矩阵A的共轭转置矩阵.
下面有关矩阵A的欧几里得范数与谱范数的不等式成立[6]:
(1)
(2)
引理1.1[7]设矩阵A和B是2个m×n矩阵,那么
‖A∘B‖2≤‖A‖2‖B‖2,
其中A∘B是A和B的Hadamard积.
引理1.2[7]设A和B是2个m×n矩阵,那么
‖A∘B‖2≤r1(A)c1(B),
其中
引理1.3当1-x2≠0时,
证明
2 主要结论
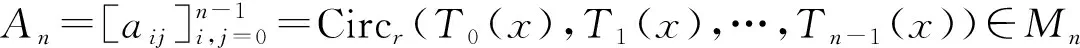
(i) 如果|r|≥1,那么
(ii) 如果|r|<1,那么
‖An‖2是矩阵An的谱范数,其中
证明
由谱范数定义可得
(i) 当|r|≥1,由引理1.3有
n+n(K1-1)=nK1.
因此
另一方面,设矩阵B和C为:
则An=B∘C有
因此
(ii) 当|r|<1时,
‖An‖E=
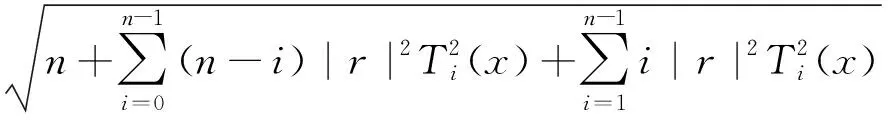
因此
另一方面,对矩阵B和C有
因此
综上
推论2.1设D=LDr(Tn-1(x),Tn-2(x),Tn-3(x),…,T1(x),T0(x))是r-左循环矩阵,则有:
(i) 如果|r|≥1,那么
(ii) 如果|r|<1,那么
‖Dn‖2是矩阵Dn的谱范数,其中
证明方法与上面相同,并有相同结果.
定理2.2设n×n矩阵
Circr(U0(x),U1(x),…,Un-1(x))∈Mn
是r-循环矩阵,则有:
(i) 如果|r|≥1,那么
(ii) 如果|r|<1,那么
‖On‖2是矩阵On的谱范数,其中
证明
由谱范数定义可得
(i) 当|r|≥1,由引理1.3有
因此
另一方面,设矩阵P和Q分别为:
则On=P∘Q,
因此
(ii) 当|r|<1时,
n+n|r|2(K2-1).
因此
另一方面,对矩阵P和Q有
因此
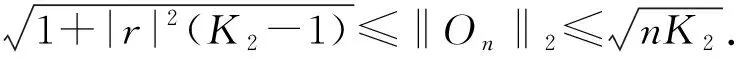
推论2.2设E=LEr(Un-1(x),Un-2(x),…,U1(x),U0(x))是r-左循环矩阵,则有:
(i) 如果|r|≥1,那么
(ii) 如果|r|<1,那么
‖En‖2是矩阵En的谱范数,其中
证明方法与定理2.2证明相同,结果相同.
因此证明了所有的结论,当r=1时,可以得到Chebyshev多项式的关于循环矩阵的谱范数的上下界估计.同样的方法适用于所有的线性递推数列或多项式.
[1] AKBULAK M, BOZKURT D. On the norms of Toeplitz matrices involving Fibonacci and Lucas numbers[J]. Hacettepe J Math Statistics,2008,37(2):89-95.
[2] AKBULAK M, BOZKURT D. On the norms of Hankel matrices involving Fibonacci and Lucas numbers[J]. Selcuk J Appl Math,2008,9(2):45-52.
[3] SOLAK S. On the norms of circulant matrices with Fibonacci and Lucas numbers[J]. Appl Math Comput,2005,37(1):125-132.
[4] GÜNGÖR A D. Lower bounds for the norms of Cauchy-Toeplitz and Cauchy-Hankel matrices[J]. Appl Math Comput,2004,157(3):599-604.
[5] SOLAK S, BOZKURT D. On the spectral norm of Cauchy-Toeplitz and Cauchy-Hankel matrices[J]. Appl Math Comput,2003,140(2):231-238.
[6] SHEN S Q, CEN J M. On the norms of circulant matrices with the (k,h)-Fibonacci and (k,h)-Lucas numbers[J]. Int J Contemp Math Science,2011(6):887-894.
[7] HORN R A, JOHNSON C R. Topic in Matrix Analysis[M]. Cambridge:Cambridge University Press,1991.
[8] GRAHAM R L, KNUTH D E, PATASHNLK O. Concrete Mathematics[M]. 2nd ed. Reading:Addison-Wesley,1994.
[9] FATIH Y, DURMUS B. Hessenberg matrices and the Pell and Perrin numbers[J]. J Number Theory,2011,131(8):1390-1396.
[10] PREDRAG S, JOVANA N IVAN. S. A generalization of Fibonacci and Lucas matrices[J]. Discret Appl Math,2008,156(14):2606-2619.
[11] ZHANG Z, ZHANG Y. The Lucas matrix and some combinatorial identities[J]. Indian J Pure Appl Math,2007,38(5):457-465.
[12] MILADINOVI M, PREDRAG S. Singular case of generalized Fibonacci and Lucas matrices[J]. J Korean Math Soc,2011,48(1):33-48.
[13] 何承源. 循环矩阵的一些性质[J]. 数学的实践与认识,2001,31(2):211-216.
[14] 何承源. 对称反循环矩阵的充要条件[J]. 四川师范大学学报(自然科学版),2011,34(3):422-426.
[15] 师白娟. 包含Chebyshev多项式的循环矩阵行列式的计算[J]. 纯粹数学与应用数学,2016,32(3):22-30.
