Zeta Functions of Zp-Towers of Curves

WAN Daqing

(University of California, Irvine, Department of Mathematics, Irvine, 92697 CA)

1 Zp-towers of curves

Let Fqbe a finite field ofqelements with characteristicp>0 and letZpdenote the ring ofp-adic integers. Consider aZp-tower

C∞:…→Cn→…→C1→C0

of smooth projective geometrically irreducible curves defined over Fq. TheZp-tower gives a continuous group isomorphism

ρ:G∞:=Gal(C∞/C0) ≅Zp.

For each integern≥0, reduction modulopngives an isomorphism

Gn:=Gal(Cn/C0) ≅Z/pnZ.

LetSbe the ramification locus of the tower, which is a subsetSof closet points ofC0. The tower is un-ramified on its complementU=C0-S. We shall assume thatSis finite.

By class field theory, the ramification locusSis non-empty, and for each non-empty finiteS, there are uncountably many suchZp-towers over Fq. In fact, allZp-towers overC0can be explicitly classified by the Artin-Schreier-Witt theory, see [1]. In contrast, if l is a prime different fromp, there are noZl-towers over Fq. Note that constant extensions do not give a tower in our sense since that would produce curves which are geometrically reducible. Thus, theZp-towers we consider are all geometricZp-towers.

≅Zp/pnZp.

These surjective homomorphisms naturally produce aZp-tower ofC0, unramified onU, which we assume to be geometric in our sense, that is, there is no constantsubextensions. This geometric tower is further called arising (or coming) from algebraic geometry ifφarises from a relativep-adic ètale cohomology of an ordinary family of smooth proper varietyXparameterized byU, or more generally in the sense of Dwork’s unit root conjecture[2]as proved in [3], that is,φcomes from the unit root part of an ordinary over convergentF-crystal onU. A classical example is the IgusaZp-tower arising from the universal family of ordinary elliptic curves over Fp, more generally, theZp-tower arising from the following Dwork family of Calabi-Yau hyper surfaces over Fpparametrized byλ:

2 Zeta functions

For integern≥0, letZ(Cn,s) denote the zeta function ofCn. It is defined by

where |Cn| denotes the set of closed points ofCn. The Riemann-Roch theorem implies that the zeta function is a rational function insof the form

P(Cn,s)∈1+sZ[s],

whereP(Cn,s) is a polynomial of degree 2gnand

gn=g(Cn)

Theq-adic valuations (also calledq-slopes) of the reciprocal roots ofZ(Cn,s) remain quite mysterious in general. Our aim is to study this question in the spirit of Iwasawa theory. Namely, we want to investigate possible stable properties for the slopes whennvaries. Classical geometric Iwasawa theory corresponds to the study of the slope zero part of the zeta function. Although much more complicated, we feel that there is a rich theory in all higher slopes, forZp-towers arising from algebraic geometry. The aim of these notes is to explore some of the basic questions, suggesting what might be true and what might be false, and giving supporting examples when available.

3 Main questions and conjectures

We now make our questions a little more precise, beginning with some simpler questions. Write

0≤vq(α1(n))≤…≤vq(α2gn(n))≤1,

where theq-adic valuation is normalized such thatvq(q)=1. We would like to understand how the polynomialP(Cn,s) (and its zeros) varies whenngoes to infinity. The first and simplest question is about the degree of the polynomialP(Cn,s).

Question3.1How the genusgnvaries asngoes to infinity?

The answer depends on how theZp-tower is given. Classically, the construction of allZp-towers was given by Witt using Witt vectors, and the genus was explicitly computed by Schmid (1937) in the same framework of Witt vectors, see [1] for a simplified complete treatment. In modern applications, aZp-tower naturally arises from algebraic geometry, and it is not clear how to compute the genus. In this direction, we propose

Conjecture3.2Assume that the tower comes from algebraic geometric. Then, the genus sequencegnis stable, that is, there are constantsa,b,cwitha>0 depending on the tower such that for all sufficiently largen, we have

gn=ap2n+bpn+c.

As an example, one can check that the conjecture is true in the case of IgusaZp-tower, using the results in Katz-Mazur[4]. The converse of the conjecture is not true. There are only countably manyZp-towers coming from algebraic geometry, but there are uncountably manyZptowers with stable genus sequence. The genus growth question was first studied in Gold-Kisilevsky[5], where a simple lower bound of the formgn≥cp2nis proved for some positive constantc. It is easy to construct towers so thatgngrows as fast as one wishes. In the joint paper with Michiel Kosters[1], we give a general explicit formula forgnvia a different explicit construction ofZp-towers. This new construction is better suited for studying the slopes of zeta functions. In this way, one can quickly read off the genus and see its variational behavior. In particular, genus stableZp-towers are completely classified in [1] in terms of a finiteness condition on our explicit Witt construction ofZp-towers. To prove the above conjecture, one needs to check that this finiteness condition is satisfied for all towers coming from algebraic geometry. This is not easy. In a forthcoming paper, Joe Krammer-Miller develops a multiplicative approach to prove this conjecture.

RemarkOne can ask the same question for the stable behavior of the discriminant of aZp-tower of number fields. Let

K=K0⊂K1⊂K2⊂…

be aZp-tower of number fields. Letdndenote the absolute discriminant ofKn. The analogue of the genus in number field is the logarithm of the discriminant. Since the prime top-part ofdnis fixed for largen, this is equivalent to asking for thep-adic valuationvp(dn). One can show [6] that for sufficiently largen,

vp(dn)=anpn+bpn+c,

wherea>0,b,care constants depending only on the tower.

We now return to the function field case. Having understood the degree of the polynomialP(Cn,s), our second natural question is about the splitting field ofP(Cn,s). In particular, how the size of the splitting field ofP(Cn,s) varies asnvaries.

Conjecture3.3LetQn(resp.Qp,n) denote the splitting field ofP(Cn,s) overQ(resp.Qp).

(1) The extension degree [Qn:Q] goes to infinity asngoes to infinity.

(2) The extension degree [Qp,n:Qp] goes to infinity asngoes to infinity.

(3) The ramification degree [Qp,n:Qp]ramgoes to infinityasngoes to infinity.

Clearly, each part is significantly stronger than its previous part. In all the examples we know, the ramification degree ofQp,noverQpalready goes to infinity, that is, the strongest part holds and thus all parts hold. Note that this conjecture is for allZp-towers, not necessarily those coming from algebraic geometry.

We now refine the above geometric genus question into many arithmetic questions in terms of slopes. Fix a rational numberα∈[0,∞), letdα(n)denote the multiplicity ofα/pnin the slope sequence ofP(Cn,s). That is,

The reason to re-scale the slope by the factor 1/pnis that the first few slopes ofP(Cn,s) is expected to be of the formα/pnfor a few rational numbersα, independent ofn. By definition,dα(n)=0 forα>pn, and

Question3.4For a fixed rational numberα∈[0,∞), how the numberdα(n) varies asngoes to infinity?

Note thatd0(n) is thep-rank of ofCn, namely, the rank of thep-adic Tate module of the Jacobian ofCn. Furthermore, the class numberhn(the number of divisor classes of degree 0 ofCn) is given by the residue formula

hn:=#Jac(Cn)(Fq)=P(Cn,1).

One has the following result from classical geometric Iwasawa theory.

Theorem3.5(i) There are integer constantsμ1andμ2such that for all sufficiently largen, we have

d0(n)=pnμ1+μ2.

(ii) There are integer constantsμ,λ,νsuch that for all sufficiently largen, we have

vp(hn)=μpn+λn+ν.

(iii) For all sufficiently largen, we have the congruence

This theorem is really about the slope zero part of the zeta function. To illustrate our new point of views, we shall give an extremely simple proof of the above result, using the definition of theT-adicL-function introduced later. It is a pleasure to thank Ralph Greenberg who asked if part (i) of the theorem is true. For higher slopeα>0, the problem is completely new and apparently more complicated.

Question3.6For each fixedα∈[0,∞), are there constantsμ1(α) andμ2(α) such that for all sufficiently largen, we have

dα(n)=pnμ1(α)+μ2(α)?

If we do not re-scale the slope in the definition ofdα(n) and look at all slopes, not necessarily the first few slopes, we can ask the following question.

Question3.7Are theq-slopes

{vq(α1(n)),…,vq(α2gn(n))}⊂

[0,1]∩Q⊂[0,1]

equi-distributed in the interval [0,1] asngoes to infinity?

A weaker version is to ask if the set ofq-slopes for allnis dense in [0, 1]. A stronger version is the following possible finiteness property.

Question3.8Is the slope sequence stable in some sense? More precisely, is there a positive integern0depending on the tower such that theq-slopes

{vq(α1(n)),…,vq(α2gn(n))}

for alln>n0are determined explicitly in a simple way by their values for 0≤n≤n0, using a finite number of arithmetic progressions?

The precise meaning of this finiteness property will be made clearer later. These three questions are too general to have a positive answer in full generality, as there are too manyZp-towers, most of them are not natural. In fact, we believe that each of the above three questions has a negative answer in full generality. It would be interesting to find examples showing that the above three questions indeed have a negative answer. However, we conjecture that the answers to all three questions are positive for allZp-towers coming from algebraic geometry. More precisely, our main conjecture is the following.

Conjecture3.9Assume that the tower comes from algebraic geometry.

(1) The genus sequencegnis stable. That is,there are constantsa,b,cwitha>0 depending on the tower such that for all sufficiently largen, we have

gn=ap2n+bpn+c.

(2) For each fixedα∈[0,∞), there are constantsμ1(α) andμ2(α) such that for all sufficiently largen, we have

dα(n)=pnμ1(α)+μ2(α).

(3) Theq-slopes

{vq(α1(n)),…,vq(α2gn(n))}⊂

[0,1]∩Q⊂[0,1]

are equi-distributed in the interval [0,1] asngoes to infinity.

(4) The slope sequence is stable. That is, there is a positive integern0depending on the tower such that theq-slopes

{vq(α1(n)),…,vq(α2gn(n))}

for alln>n0are determined explicitly by their values for 0≤n≤n0, using a finite number of arithmetic progressions.

We shall make part (4) of the conjecture more precise later and give some supporting examples. Parts (2)-(4) of the conjecture are in increasing level of difficulties. Each of parts (1)-(3) is a weak consequence of part (4). Thus, a proof for each of parts (1)-(3) is also an evidence for the strongest part (4) of the conjecture. Recent work of Kosters-Zhu[7]suggests that part (1) always implies part (3), which has been proved whenUis the affine line.

Before moving on, we note the following consecutive divisibility

P(C0,s)|P(C1,s)|…|P(Cn,s)|….

Thus, it is enough to study forn≥1, the primitive part ofZ(Cn,s) defined by

4 L-functions

Note that ifCnis ramified overC0at a closed pointx∈S, thenCmis totally ramified overCnatxfor allm≥nsince the Galois group is a cyclicp-group. Without loss of generality, by going to a largernif necessary, we can assume thatC1is already ramified at every point ofS. From now on, we assume thatC1is indeed (totally) ramified at every point ofS.

Recall that forn≥1, the Galois group

Gn=Gal(Cn/C0)≅Z/pnZ.

For a primitive character

of orderpn>1, theL-function ofχnoverC0is

1+sZ[χn(1)][[s]],

where |U| denotes the set of closed points ofUandFrobxdenotes the arithmetic Frobenius element ofGnatx. Note thatζpn:=χn(1) is a primitivepn-th root of unity. Again, Weil’s theorem shows that theL-functionL(χn,s) is a polynomial ins, pure of weight 1. One has the decomposition

whereχndenotes a primitive character of orderpn.For

σ∈Gal(Q(ζpn)/Q)=Gal(Qp(ζpn)/Qp),

one checks that

It follows that the degree and the slopes forL(χn,s) depend only onn, not on the choice of the primitive characterχnofGn. We can just choose and fix one characterχnof orderpnfor eachn≥1, if desired.

The extension degree conjecture for the splitting field ofP(Cn,s) is reduced to

Conjecture4.1LetLp,ndenote the splitting field ofL(χn,s) overQp.

(1) The extension degree [Lp,n:Qp] goes to infinity asngoes to infinity.

(2) The ramification degree [Lp,n:Qp]ramgoes to infinity asngoes to infinity.

Let l (n) denote the degree of the polynomialL(χn,s). The degree ofQ(Cn,s) is simply

pn-1(p-1)l (n).

The genusgnofCnis given by the formula

To understand the variation ofgnasnvaries, it is enough to understand the variation of l (n) asnvaries. Conjecture 3.2 is equivalent to

Conjecture4.2Assume that the tower comes from algebraic geometry. Then, the degree sequence l (n) is stable in the sense that there are constantsa,bwitha>0 depending on the tower such that for all sufficiently largen, we have

l (n)=apn+b.

Again, this conjecture can be refined in terms of slopes.Write

0≤vq(β1(n))≤…≤vq(βl (n)(n))≤1.

The slope sequence forQ(Cn,s) is just equal to the slope sequence forL(χn,s), repeatedpn-1(p-1) times.

Fix a rational numberα∈[0,∞), let lα(n) denote the multiplicity ofα/pnin the slope sequence ofL(χn,s). That is,

It is clear that for everyn≥1, we have

and for everyα, we have

Question4.3For a fixed rational numberα∈[0,∞ ), how the number lα(n) varies asngoes to infinity?

In the caseα=0, the situation is quite simple and clean. The following result follows quickly from the definition ofT-adicL-functions introduced later.

Lemma4.4For everyn≥1, we have

In particular, the number l0(n) forn≥1 is a constant independent ofn. It follows that

Substituting the value of l0(1) in the lemma, we get an alternative formula ford0(n):

d0(n)-d0(0)=

This proves part (i) of Theorem 3.5. It implies that the sequence {d0(n)}n≥0is determined by the first two termsd0(0) andd0(1). Alternatively, it is determined by the first termd0(0) and the degree of the divisorS. Forα>0, the slope sequence {dα(n)}n≥0is more complicated. Similar to the zeta function case, we can ask

Question4.5(1) For each fixedα∈[0,∞), the number lα(n) is a constant for all sufficiently largen?

(2) Asngoes to infinity, are theq-slopes

{vq(β1(n)),…,vq(βl (n)(n))}⊂

[0,1]∩Q⊂[0,1]

equi-distributed in the interval [0, 1]?

(3) Is there a positive integern0depending on the tower such that theq-slopes

{vq(β1(n)),…, vq(βl (n)(n))}

for alln>n0are determined explicitly by their values for 0≤n≤n0, using a finite number of arithmetic progressions?

Again, these questions are too general to have a positive answer in full generality. However, we conjecture all of them have a positive answer forZp-towers coming from algebraic geometry. To gain some feeling what part (3) means, we give an example next.

5 Zp-towers over the affine line

In this section, we explain that all the above questions for all slopes have a simple positive answer for manyZp-towers over the affine line, as first studied in [8], and more recently in [7-14].

Fix an elementβofW(Fq)=Zqwith trace 1. By the classification in [1], anyZp-tower overC0=P1, totally ramified at infinity ∞ and unramified on

A1=P1-{∞}

can be uniquely constructed from a constantc∈Zpand a primitive convergent power series

wheref(x) is called primitive if not allciare divisible byp, that is,f(x) is not divisible byp. The construction is explicitly given by the following equation

where both sides are Witt vectors. The constantchas no contribution to all our questions, and thus we shall asumme thatc=0.The tower is then uniquely constructed from the primitive convergent power seriesf(x).Comparing the coordinates, one finds thatCnis defined by a system ofnpolynomial equations over Fqinn+1 variables (y1,…,yn,x). It is clear that

C0=P1,

C1is the Artin-Schreier curve whose affine equation over Fqis given by

andC2is the curve aboveC1given by an additional equation (over Fq)

where

andσis the Frobenius automorphism onZq. Note that over Fq, the power seriesf(x) reduces to a polynomial.

The mapCn→Cn-1is given by the projection

(y1,…,yn,x)→(y1,…,yn-1,x).

tn=ζpn-1,

which is a uniformizer in the local fieldQp(ζpn).For alln≥1, it is clear thatχn≡1modtnand

L(χn,1)≡Z(A1,1)≡1modtn.

We obtain

Theorem5.1Lethndenote the class number ofCn. Then, for alln≥0, we have

hn≡1modp.

In particular,d0(n)=l0(n)=μ=λ=ν=0.

It would be interesting to explore possible improvements of the above congruence to a congruence modulo higher powers ofp, that is, to understand the first few digits in thep-adic expansion ofhn.

For integern≥1, the Artin conductora(χn) of the characterχnis calculated explicitly in [1]:

It follows that the degree ofL(χn,s) is given by the formula

This tower is genus stable precisely when

exits and is a finite rational number, in which case, for all sufficiently largen, we have the stable degree formula

l (n)=dpn-1-1.

Definition5.2Assume that the tower is genus stable. Letn0be the smallest positive integerksuch that

l (k)=pk-1d-1,

and if theq-slope sequence ofL(χk,s) is denoted by {α1,…,αpk-1d-1}, then for every integern≥k, theq-slope sequence ofL(χn,s) is given by

If such positive integerkdoes not exist, we definen0=∞.

The finiteness of the numbern0hence implies a striking stable property for the slope sequence ofL(χn,s) asngoes to infinity. It implies that the slopes ofL(χn,s) normalized by the factorpnfor all largenare given by a finite number of arithmetic progressions. For this reason, the tower is calledslopestableifn0is finite. Note that if the tower is slope stable, then clearly the tower must be genus stable. It is tempting to conjecture that the converse is also true. Although we do not have a counter-example, we are a little cautions here and will just state it as a question.

Qnestion5.3Assume the tower is genus stable. Is the tower slope stable?

Note that we conjectured that the answer is positive for towers coming from algebraic geometry. An important example is the IgusaZp-tower which is genus stable, but the finiteness property ofn0for Igusa tower seems open. This might be related to the geometry of eigen curves in the framework of modular forms, see [9-10] for a recent progress and [11] for a precise conjectural slope description in the case of regular primesp. Another related slope problem in the setting of symmetric powers of Kloosterman sums is recently studied in Haessig[12].

We now give some examples ofZp-towers constructed using the primitive convergent power seriesf, where the above question has a positive answer.

Definition5.4(1) The tower is called apolynomialtowerof degreedif the primitive convergent power series

is a polynomial of degreed.

(2) The tower is called aunitroottowerof degreediff(x) is a polynomial of degreedand furthermore all non-zero coefficientsciare roots of unity.

Clearly, a polynomial tower is genus stable (the converse is not true) and its degreedis not divisible byp.

Theorem5.5[8]For a unit root tower of degreed, the numbern0is finite. Furthermore, we have the following explicit upper bound

In particular, if

thenn0≤2.

Corollary5.6For a unit root tower of any degree, we have the following

(1) Theq-slopes ofL(χn,s) (resp.,P(Cn,s)) are equi-distributed in [0,1] asngoes to infinity.

(2) For every rational numberα∈[0,∞), the sequence lα(n) is a constant independent ofn≥n0.

(3) The ramification degree ofP(Cn,s) overQpgoes to infinity asngoes to infinity.

The above explicit bound forn0can be improved in various special cases.

Example5.7For a unit root tower of degreedsatisfying

p≡1modd,

we haven0=1,αi=i/dfor 1≤i≤dand hence the slope sequence ofL(χn,s) for alln≥1 is given by

This was first proved in [13]. TheT-adicL-function introduced there plays a crucial role in the proof of the above more general theorem.

Example5.8Let

f(x)=xd+ax∈Zq[x]

withaq-1=1,dnot divisible bypand

It is proved in [15] thatn0=1 and

The slope stable property is now proved to be true for any polynomial tower in [14] and more generally for a much larger class of genus stable towers over the affine line in [7]. TheT-adicL-function introduced in next section played an essential role in [8] and [14]. A novel feature of [7] is the introduction of theπ-adicL-function in infinitely many variables which refines and interpolates theT-adicL-function. It would be interesting to prove the slope stable property for all genus stable towers or to find a counter-example.

6 T-adic L-functions

ρ:G∞≅Zp

is crucial for us. Thep-adic valued Frobenius function it induces

Fρ:|U|→Zp,Fρ(x)=ρ(Frobx)

determines theZp-tower by class field theory. Any condition we would impose on the tower is a condition on this Frobenius functionFρ.

Consider the universal continuousT-adic characterZp→Zp[[T]]*determined by sending 1 to 1+T. Composing this universalT-adic character ofZpwith the isomorphismρ, we get the universalT-adic character ofG∞:

ρT:G∞→Zp→GL1(Zp[[T]])=Zp[[T]]*.

(1)

The open unit diskDp(1) parametrizes all continuousCp-valued charactersχofG∞via the relation

t=χ(1)-1.

TheL-function ofρtis defined in the usual way:

1+sCp[[s]].

In the case thatχ=χnis a finitep-adic character ofG∞of orderpn, thenχ(1) is a primitivepn-th roots of unity and we have

L(χn,s)=L(ρtn,s).

Elements of the formtn=χn(1)-1 forn≥0 are called the classical points inD(1). Asngoes to infinity,tnapproaches to the boundary of the diskDp(1). Thus, to understand the behavior ofL(χn,s) asngrows, it is enough to understand theL-functionL(ρt,s) for alltnear the boundary ofDp(1). More precisely, we should understand the following universalL-function.

Definition6.1TheT-adicL-function of the tower is theL-function of theT-adic characterρT:

Lρ(T,s):=L(ρT,s)=

1+sZp[[T]][[s]].

This is ap-adic power series in the two variablesTands.Fort∈Dp(1), we have

L(ρt,s)=Lρ(T,s)|T=t=Lρ(t,s).

As noted above, the specialization ofLρ(T,s) at every classical pointT=tnis a rational functionLρ(tn,s) ins, in fact, a polynomial insof degree l (n) forn≥1. In this case, the characterρtnis of finite order. Ift∈Dp(1) is not a classical point, i.e.,ρtis of infinite order, we do NOT know a single example for whichLρ(t,s) is rational.

Question6.2Is there a non-classical

t∈Dp(1)

such thatLρ(t,s) is rational?

To see the significance of theT-adicL-function, we now use the definition ofLρ(T,s) to prove Theorem 3.5. Since the characterρTis trivial moduloT, theL-functionLρ(T,s) moduloTis the same as the zeta functionZ(U,s) ofU. This gives the congruence

ReplacingTbytnforn≥1, we deduce

Comparing the number of reciprocal roots of slope zero, one finds that forn≥1,

This proves Lemma 4.4 and hence part (i) of Theorem 3.5.

To get the stable formula forvp(hn), we need to specializesat 1. Write

Lk(T) ∈Zp[[T]].

SinceLρ(tn,s) is a polynomial of degree l (n), we haveLk(tn)=0 for allk>l (n). Thep-adic Weierstrass preparation theorem implies that

uk(T)∈Zp[[T]]

for allk>l (n). It follows that the seriesLρ(T,s) is (p,T)-adically convergent fors∈Zp[[T]]. Takings=1, noting thatLρ(T,1)≠0 as its specialization at classical pointstnis non-zero, we can write

Lρ(T,1)=

pμ(Tλ+pa1Tλ-1+…+paλ)u(T),

whereai∈Zpandu(T) is a unit inZp[[T]]. It follows that

vp(hm)-vp(h0)=

Sincevp(u(tn))=0, and for

pn-1(p-1)>λ,

we have

we conclude the stable formula that formsufficiently large,

vp(hm)=μpm+λm+ν

for some constantν. Part (ii) of Theorem 3.5 is proved.

Finally, note that forn≥1, we have

The minimal polynomial oftnis thep-Eisenstein polynomial

Thus, forn≥2 (orp>2), we have

NormQp(tn)/Qp(tn)=p,

NormQp(tn)/Qp(u(tn))≡1modp,

whereu(T) is any unit inZp[[T]]. It follows that for sufficiently largen,

Part (iii) of Theorem 3.5 is proved.

7 T-adic Meromorphic continuation

The power series ringZp[[T]] has three obvious topologies: thep-adic topology, theT-adic topology and the (p,T)-adic topology. All these topologies are useful to us. In this section, we will focus on theT-adic topology, which will be our starting point.

ViewingLρ(T,s) as a power series inswith coefficients in the complete discrete valuation fieldQp((T)) with uniformizerT, we are interested in theT-adic meromorphic continuation. Clearly,Lρ(T,s) isT-adic analytic in theT-adic open unit disk |s|T<1. One can prove

Proposition7.1There is a decomposition

where

Di(T,s)∈1+sZp[[T]][[s]]

areT-adic analytic on |s|T≤1 for 1≤i≤2. Furthermore,

D2(T,s) ∈1+qsZp[[T]][[s]].

Corollary7.2(i)Lρ(T,s) isT-adic meromorphic on the closedT-adic unit disk |s|T≤1, i.e., well defined fors∈Qp[[T]].

(ii)Lρ(T,s) is (p,T)-adic analytic on the closed (p,T)-adic unit disk |s|(p,T)≤1, i.e., convergent fors∈Zp[[T]].

Part (ii) of the corollary was already proved in the previous section. Crew [17] further showed that the (p,T)-adic slope zero part ofLρ(T,s) has a cohomological interpretation in terms ofp-adic ètale cohomology. This is the main conjecture in function fields. Note that part (i) of the corollary is stronger. It cannot be deduced from the results in [17].

To understand higher slopes of theZp-tower, we need to study the analytic properties of the two variable functionLρ(T,s) beyond the closed unit disk

|s|T≤1.

This leads to the following two questions.

Question7.3For which tower, theL-functionLρ(t,s) isp-adic meromorphic in

|s|p<∞

for allt∈Dp(1).

Question7.4For which tower, theT-adicL-functionLρ(T,s) isintegrallyT-adic meromorphic in |s|T<∞ in the sense that

where

Di(T,s)∈1+sZp[[T]][[s]]

areT-adic analytic in |s|T< ∞ for 1≤i≤2.

The second question is stronger than the first one, as the integrallyT-adic meromorphic continuation ofLρ(T,s) implies thep-adic meromorphic continuation ofLρ(t,s) for allt∈Dp(1). There are examples whereLρ(t,s) is notp-adic meromorphic, see [18]. Thus, some conditions are necessary to have a positive answer.

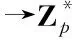
Theorem7.5Assume thatMρis ∞log-convergent onU. ThenLρ(T,s) is integrallyT-adic meromorphic in |s|T< ∞. It follows thatLρ(t,s) isp-adic meromorphic in

|s|p<∞

for allt∈Dp(1).

This result is not general enough for applications, although both the unit root tower and the polynomial tower do satisfy the condition of the above theorem. More generally, the method in [3] can be used to prove the following Coleman’s generalization of the rank once case of Dwork’s unit root conjecture. In fact, this was already worked out in Grosse-Klönne[20]in the case thatMρcomes from a pure slope piece of some finite rank over convergentσ-module onU.

Theorem7.6Assume thatMρcomes from a pure slope piece of some finite rank ∞log-convergentσ-module onU. ThenLρ(T,s) is integrallyT-adic meromorphic in |s|T< ∞. It follows thatLρ(t,s) isp-adic meromorphic in |s|p< ∞ for allt∈Dp(1).

In all natural applications arising from higher dimensional arithmetic geometry, the rank oneσ-moduleMρsatisfies the assumption of Theorem 7.6, but usually not the assumption of Theorem 7.5. These results make it possible to talk about the zeros and poles of theL-functionLρ(T,s) ifρcomes from algebraic geometry.

We can now state theL-function version of our main conjecture, which answers Question 4.5 and is equivalent to Conjecture 3.9(the zeta function version of our main conjecture).

Conjecture7.7Assume that theZp-tower comes from algebraic geometry.

(1) TheL-degree is stable. That is, there are constantsa,bwitha>0 such that for sufficiently lawgen, we have l (n)=apn+b.

(2) For each fixed rational numberα∈[0,∞), the number lα(n) is a constant for all sufficiently largen.

(3) Theq-slopes ofL(χn,s) are equi-distributed in [0,1] asngoes to infinity.

(4) The slopes are stable. That is, there is a positive integern0depending on the tower such that theq-slopes

{vq(α1(n)),…,vq(α2gn(n))}

for alln>n0are determined explicitly by their values for 0≤n≤n0, using a finite number of arithmetic progressions.

Part (1) is just Conjecture 4.2 stated previously, which is equivalent to Conjecture 3.2 on the genus stable property. The remarkable work of Kosters-Zhu suggests that part (1) always implies part (3) for anyZp-tower. In fact, they have proved this implication for allZp-towers over the affine line. As seen above, this main conjecture is completely proven for manyZp-towers over the affine line. An important example to consider is the IgusaZp-tower over Fpfor which the full conjecture seems still open. This example is important because of its possible connection to arithmetic of modular forms and Galois representations. In fact, part of our conjecture was motivated by Coleman-Mazur’s question[21]on the geometry of the eigencurve near the boundary of the weight disk, see the introduction in [10] for additional information. Loosely speaking, the eigencurve (or its spectral curve) is the “zero locus” of the two variableL-functionLρ(T,s). The eigencurve was introduced to extend Hida’s theory from slope zero to all higher slopes. In one aspect, our general conjecture can be viewed as an attempt to extend geometric Iwasawa theory from slope zero to all higher slopes.

[1] KOSTERS M, WAN D Q. Genus growth inZp-towers of function fields[J]. Proc Am Math Soc,arXiv:1703.05420.

[2] DWORK B. Normalized period matrices II[J]. Math Ann,1973,98:1-57.

[3] WAN D Q. Rank one case of Dwork’s conjecture[J]. J Am Math Soc,2000,13(4):853-908.

[4] KATZ N, MAZUR B. Arithmetic Moduli of Elliptic Curves[M]. Annals of Mathematics Studies 108. Princeton NJ:Princeton University Press,1985.

[5] GOLD R, KISILEVSKY H. On geometricZp-extensions of function fields[J]. Manuscripta Math,1988,62:145-161.

[6] TATE J T.p-divisible Groups[M]. Driebergen:Proc Conf Local Fields,1966.

[7] KOSTERS M, ZHU H J. Slopes ofL-functions in genus stableZp-covers of the projective line[J]. J Number Theory,arXiv:1701.08733v3.

[8] DAVIS C, WAN D Q, XIAO L. Newton slopes for Artin-Schreier-Witt towers[J]. Math Ann,2016,364(3/4):1451-1468.

[9] WAN D Q, XIAO L, ZHANG J. Slopes of eigencurves over boundary disks[J]. Math Ann,2017,369(1/2):487-537.

[10] LIU R, WAN D Q, XIAO L. Slopes of eigencurves over the boundary of the weight space[J]. Duke Math J,2017,166(9):1739-1787.

[11] BERGDALL J, POLLACK R. Slopes of modular forms and the ghost conjecture[J]. IMRN,arXiv:1607.04658.

[12] HAESSIG D.L-functions of symmetric powers of Kloosterman sums (unit rootL-functions andp-adic estimates)[J]. Math Ann,2017,369(1/2):17-47.

[13] LIU C, WAN D Q.T-adic exponential sums over finite fields[J]. Algebra Number Theory,2009,3(5):489-509.

[14] LI X. The stable property of Newton slopes for polynomial Witt towers[J]. J Number Theory,2018,185:144-159.

[15] OUYANG Y, YANG J. Newton polygons of L functions of polynomialsxd+ax[J]. J Number Theory,2016,160:478-491.

[16] LIU C, LIU W, NIU C. GenericT-adic exponential sums in one variable[J]. J Number Theory,2016,166:276-297.

[17] CREW R.L-functions ofp-adic characters and geometric Iwasawa theory[J]. Invent Math,1987,88(2):395-403.

[18] WAN D Q. Meromorphic continuation ofL-functions ofp-adic representations[J]. Math Ann,1996,143:469-498.

[19] MONSKY P. Formal cohomology III[J]. Math Ann,1971,93(2):315-343.

[20] GROSSE-KLÖNNE E. On families of pure slopeL-functions[J]. Documenta Math,2003,8:1-42.

[21] COLEMAN R, MAZUR B. The Eigencurve, In Galois Representations in Arithmetic Algebraic Geometry[M]. Cambridge:Cambridge Univ Press,1998:1-113.

[22] REN R, WAN D Q, XIAO L, et.al. Slopes for higher rank Artin-Schreier-Witt towers[J]. Trans Am Math Soc,arXiv:1605.02254.

[23] KRAMER-MILLER J. The monodromy ofF-isocrystals with logarithmic decay[J]. arXiv:1612.01164.