基于空间直角阵列的改进2D-MUSIC算法
2018-07-04黄海涛
肖 峻,张 欣,黄海涛
(武汉理工大学 机电工程学院,湖北 武汉 430070)
波达方向估计(direction of arrival,DOA)在智能天线、声纳、电子侦查等领域有着广泛的应用,是目前阵列信号处理的一个重要研究内容[1-2]。2D-MUSIC算法是二维DOA估计的经典算法,可以计算渐进无偏估计,但由于要进行二维穷尽搜索,计算量很大,不适用于工程实际应用[3]。后来,一些专家学者提出了一些基于常规阵列的改进算法,如二维Root-MUSIC算法[4]、二维ESPRIT算法[5]等,这些算法虽然减小了计算量,但却存在参数匹配等问题[6]。
针对上述问题,笔者从阵列的结构考虑,提出了基于三坐标的空间直角阵列的改进2D-MUSIC算法。该算法利用空间直角阵列中通过俯仰角以及方位角就能确定声源方向的特点,从降低搜索维度和压缩搜索范围这两个方面对2D-MUSIC算法进行了改进。该算法基本原理与2D-MUSIC算法相同,但添加了方位角的一维匹配搜索以及变步长搜索。由于变步长搜索最终步长与2D-MUSIC算法的搜索步长相同,从而保证改进算法与原算法精度相同。由于变步长搜索次数大幅减小,与原算法相比定位速度更快,可满足工程实际应用的要求。
1 阵列结构和信号模型
图1为所设计的空间直角阵列,该阵列由X、Y、Z3个方向的均匀线阵以及原点麦克风O组成,每个线阵上均匀分布着间距为d的n个麦克风,分别以Ai、Bi、Ci(i=1,2,…,n)表示。设声源位置矢量OS与X、Y、Z轴正方向的夹角分别为αx、αy、αz,OS与Z轴正方向的夹角为仰角θ,OS的投影与Y轴正方向的夹角为方向角β,则它们的关系为:
(1)
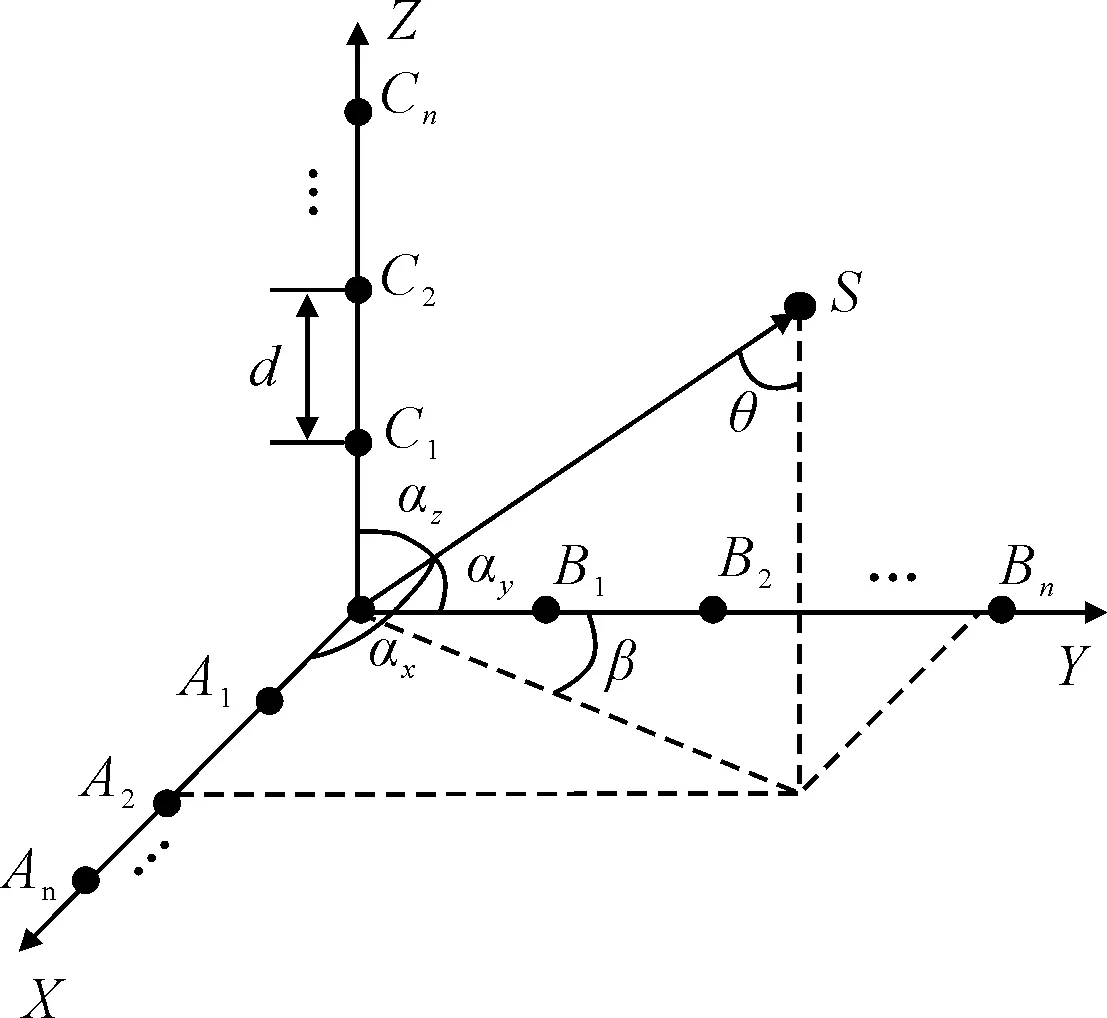
图1 空间直角阵列模型
2 改进2D-MUSIC算法
2.1 2D-MUSIC算法
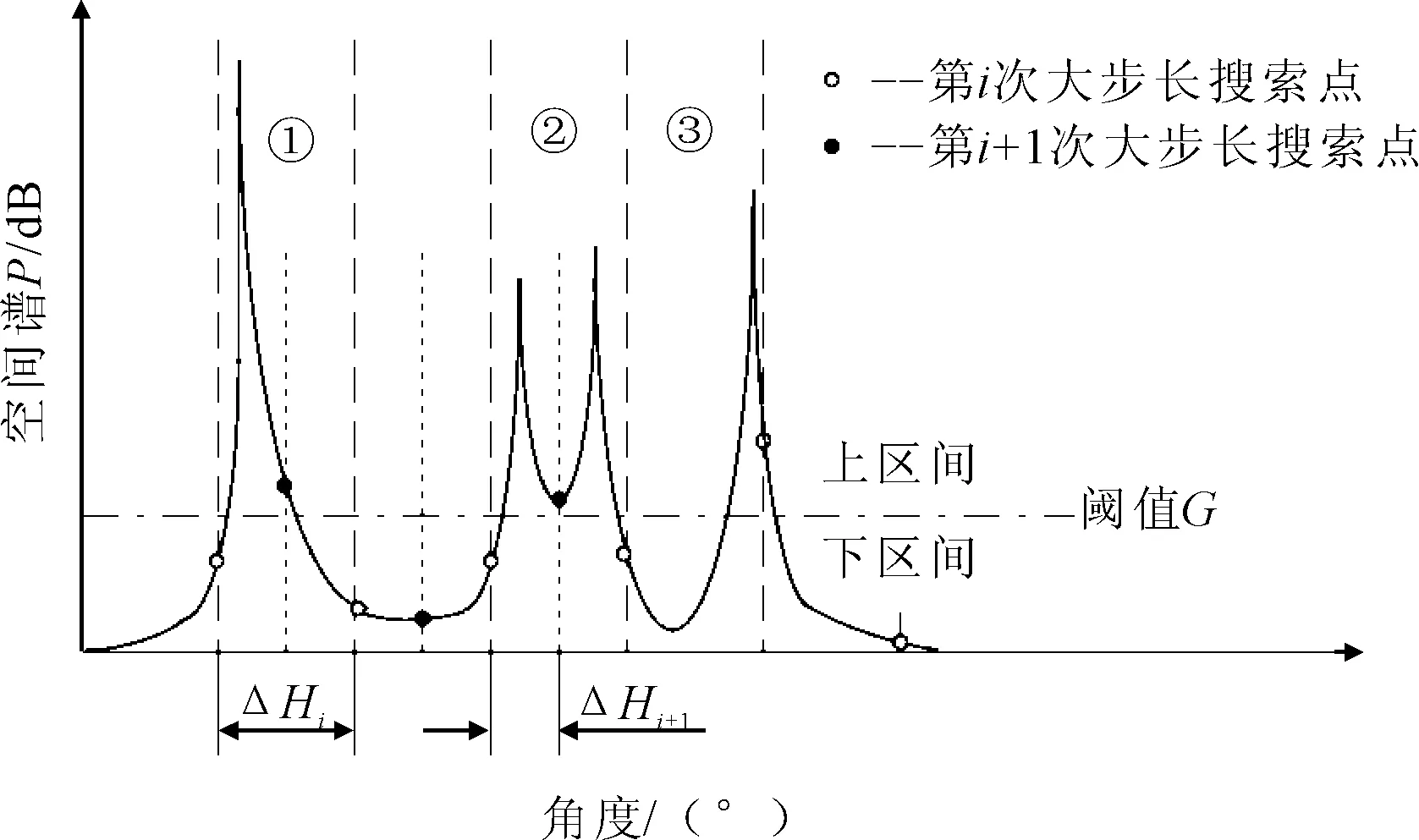
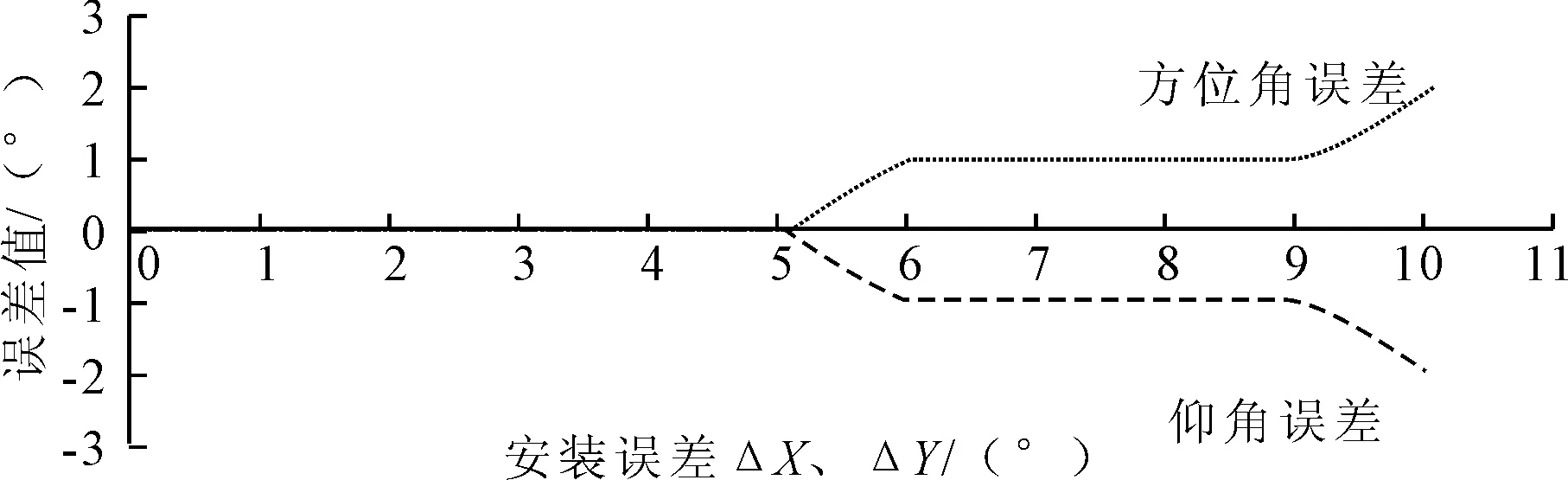
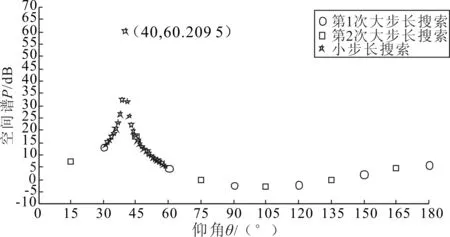
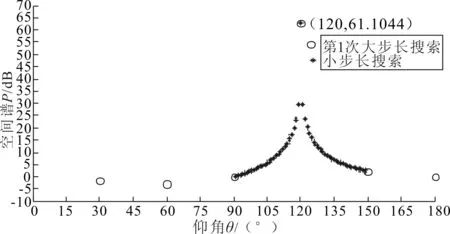
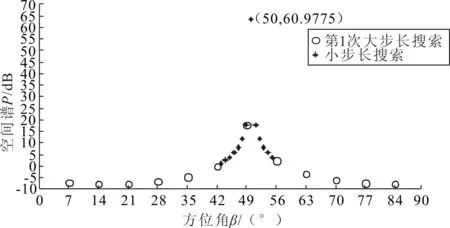
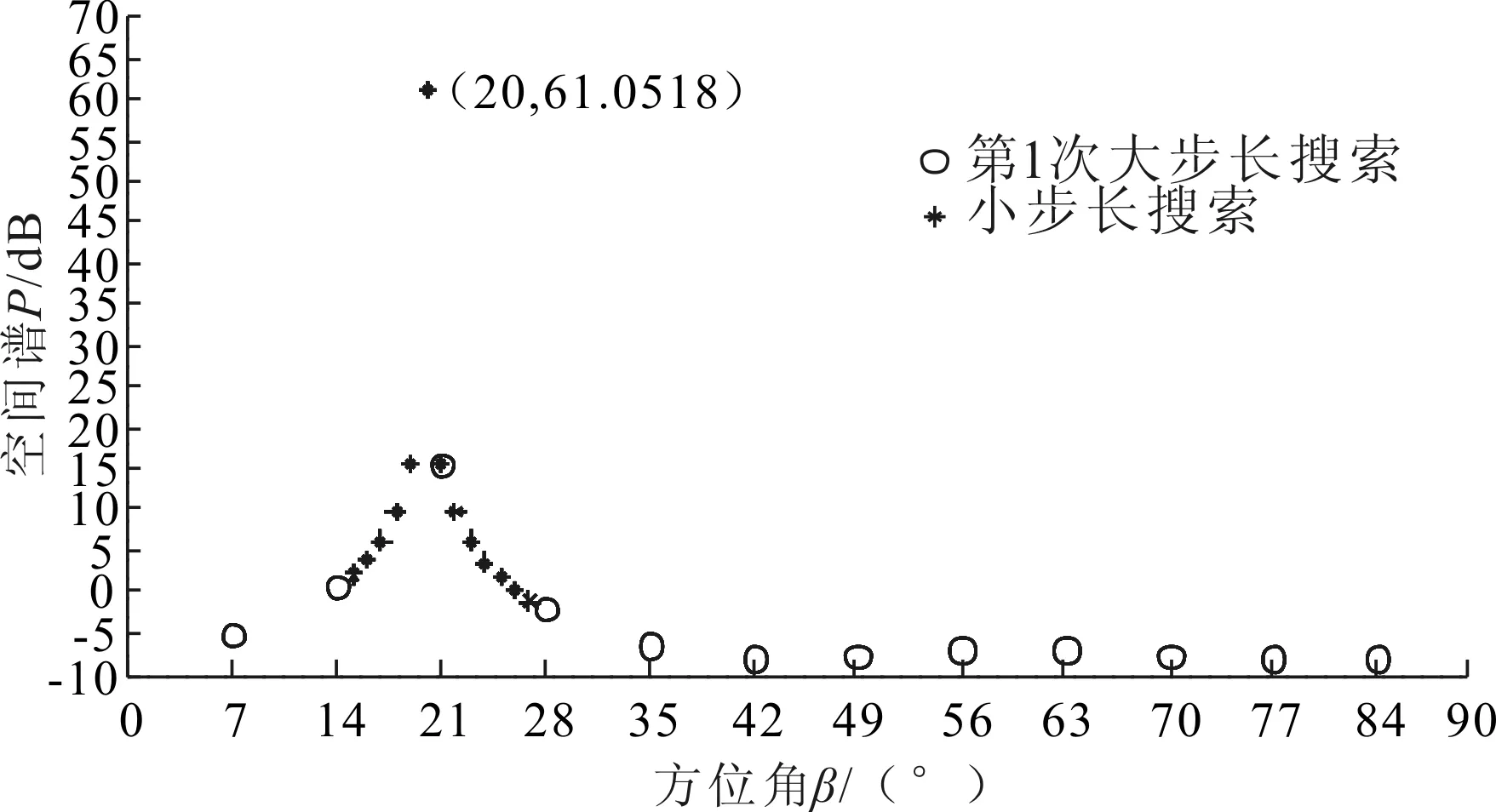
设有M(M N=Axy(θ,β)S(t)+N (2) 式中:Axy=[a(θ1,β1),a(θ2,β2),…,a(θM,βM)]为X、Y向阵列导向矢量矩阵;S(t)为M个信号源矩阵;N为噪声信号矩阵。 设M(t)的协方差矩阵特征分解后所构成的噪声子空间为UNoise,建立的二维空间搜索谱为: (3) 2D-MUSIC算法就是通过对式(3)的穷尽搜索,从而估计声源方位信息。对于仰角θ为(0°,180°]、方位角β为(0°,90°]的搜索空间,若取搜索步长为0.1°,则2D-MUSIC需完成1 800×900次搜索,计算量很大,实时性较差,不适用于工程实际应用。 2.2.1 降低搜索维度 相比于2D-MUSIC算法,笔者首先利用Z向线阵和一维MUSIC算法估计信号源的仰角,建立的Z向信号接收模型Z(t)为: =Az(θ)S(t)+N (4) 式中,Az=[az(θ1),az(θ2),…,az(θM)]为Z向阵列导向矢量矩阵。 设Z(t)的协方差矩阵特征分解后所构成的噪声子空间为UNoise-z,则根据Z(t)建立一维MUSIC空间搜索谱为: (5) 通过对式(5)的一维搜索能快速准确定位到各信号源的仰角(θ1,θ2,…,θM)。最后,将已知的各声源仰角依次带入式(3),得到方位角的匹配搜索谱函数。如式(6)所示: k=1,2,…,M (6) 从式(6)可以看出,之后只需进行M次一维搜索便可确定与各仰角相对应的方位角(β1,β2,…,βM)。同样,取搜索步长为0.1°,本算法的搜索次数为(2+M)×900次。下文仿真中的2声源定位,改进后的算法与2D-MUSIC算法相比,在精度为0.1°不变的基础上,搜索次数由原本的1 800×900次大幅减少到4×900次。同时,与二维Root-MUSIC算法相比,该搜索方式有效避免了方位角与俯仰角的匹配问题[7-8]。 2.2.2 压缩搜索范围 变步长搜索在一维参数搜索中作用明显,而本文通过阵列结构可将二维搜索分解为两个一维搜索,因此可将变步长搜索嵌入其中,进一步提高搜索效率。 图2 典型谱峰分布图 图2为谱峰分布的典型情况举例,阈值G的取值在谱峰峰值与平坦的空间谱值之间,它将空间谱划分为上、下两个区间。阈值G的选取可以由声源角度附近几个搜索点的谱值加权得到,具体可参考文献[9]中对阈值G的描述。设初始搜索大步长为ΔH1,ΔH1大于每个谱峰宽度,搜索范围为[0°,180°],搜索点的个数为Q1=1+180/ΔH1。假如某搜索点处的谱值大于阈值G,那么可认为在该点处附近至少存在1个谱峰,对该点处邻域宽度为k1的范围内进行小步长为Δh1的精确搜索,便可得到该点处的谱峰个数。其中,小步长Δh1用于控制精度,若搜索所得谱峰数小于声源数目,大步长ΔH2取ΔH1/2进行第2次大步长搜索,重复上述过程,直到谱峰数与声源数目对应。大步长的搜索点数等效于以步长ΔN搜索为一次搜索的次数,而小步长的搜索次数与邻域宽度和搜索精度有关。通常,搜索精度是确定的,因此各小步长是相等的。而考虑到峰值点可能在某个大步长区间的边界处(图2中①、③区域),或者某个大步长内存在多个波峰(图2中②区域)等情况,为避免搜索过程中出现遗漏谱峰的情况,邻域ki需满足 (7) 综上所述,通过变步长搜索法,可以减少一维谱峰搜索的搜索次数。并且通过控制小步长的搜索精度,能达到与MUSIC算法全局遍历搜索同样的精度。 在MATLAB软件中,取声源模拟信号分别为s1(t)=sin(2πt),s2(t)=sin(2πt+1)。取X、Y、Z向阵元数均为2的7阵元空间直角型阵列,间距波长比为0.5,N样本=50 000,SNR=40 dB,模拟信号s1、s2的入射角度(θ,β)分别取(40°,50°)、(120°,20°)。θ搜索范围取(0°,180°],β搜索范围取(0°,90°],为保证与2D-MUSIC算法同样的搜索精度,设置初始搜索大步长为30°,小步长为1°,阈值G=10 dB,Z向阵列的搜索结果如图3所示。 图3 Z向线阵变步长搜索谱 将已知仰角分别带入Pxy(θ,β)进行一维变步长搜索,这时可根据Z向搜索的结果设定仿真声源s1的初始步长为8°,s2的初始步长为7°,小步长为1°,搜索的范围为θ1=40°的平面和θ2=120°的平面。通过式(6)对方位角进行变步长搜索,搜索结果如图4所示。最后,通过谱峰识别可准确提取s1、s2声源的方位。 图4 β角的搜索结果 在不同信噪比下,取声源的方位为(5°,10°),分别运用笔者提出的算法和2D-MUSIC算法进行100次仿真。定义均方根误差为: (8) 其中θn、βn分别表示第n次估计的方位角和仰角。 估计方差随信噪比的变化规律如图5所示。由图5可知,本文算法与2D-MUSIC算法的估计精度相当。 图5 估计方差随信噪比的变化规律 在仿真基础上进行100次仿真实验,统计本文算法和2D-MUSIC算法的耗时,结果如表1所示。从表1可以看出,本文算法降低了运算量,大幅提高了运算速度。 表1 算法耗时比较 上述仿真是建立在理想阵列的条件上,而在实际阵列安装中,很难保证空间直角阵列两两垂直,下面分析阵列位置误差对定位精度的影响。设Δx、Δy分别为X、Y方向线阵与理想阵列的Y轴、X轴的夹角偏差,Δd为阵列间距d的安装偏差。如图6和图7所示,若要保证方位角和仰角的定位误差在1°以内,需满足夹角偏差Δx、Δy在4°以内,间距偏差Δd在15 mm以内。由此可以看出,该误差范围在工程上容易保证,从而证明了该阵列的可行性。 图6 夹角偏差对定位精度的影响 图7 间距偏差对定位精度的影响 在30 m×15 m×15 m厂房里,分别采集单独工作时图8中的左侧电机A与右侧电机B的噪声信号,采样率设置为22.05 kHz,采样时间设置为1.5 s。 图8 实验电机 固定样本采用FFT变化得到的频谱图观测。采样信号生成的时域波形图、频谱图和时频分布图如图9所示。 图9 A、B电机的声源信号图 使用扬声器将A电机噪声以仰角40°、方位角50°的角度,B电机噪声以仰角120°、方位角20°的角度辐射至该阵列模型上。利用SOBI算法对Z向阵列接收信号进行盲源分离,再利用TCT算法进行子带划分和聚焦,具体处理方法在此不做赘述。最后,设阈值G=15 dB,搜索精度为1°,通过改进2D-MUSIC算法分别对A、B电机进行定位。 如图10~图13所示,信号1在仰角40°、方位角50°的方向,信号2在仰角120°、方位角20°的方向。其中,信号1为A电机噪声,信号2为B电机噪声。估计精度为1°,定位时间为0.141 s。因此,该算法能较为精准地估计电机的方位。 图10 信号1的θ角聚焦定位结果 图11 信号2的θ角聚焦定位结果 图12 信号1的β角聚焦定位结果 图13 信号2的β角聚焦定位结果 笔者以空间直角接收阵列的阵元为基础,在2D-MUSIC算法的原理基础上,提出一种基于降维搜索与变步长搜索相结合的改进2D-MUSIC算法。在空间谱峰搜索过程中,将二维谱峰搜索降维到一维的俯仰角搜索和一维的方位角匹配搜索,大大降低了计算量,避免了二维Root-MUSIC算法和二维ESPRIT算法中的俯仰角与方位角的匹配问题。同时,在俯仰角和方位角搜索过程中,加入了变步长搜索方法,在相同定位精度下进一步缩短了搜索所需时间。通过实验证明了本算法的有效性。 参考文献: [1] Chen Haihua, Pan Zhengang, Tian Lin,et al. A Novel AWSF Algorithm for DOA Estimation in Virtual MIMO Systems[J]. IEEE Journal on Selected Areas in Communications, 2013,31(10):1994-2003. [2] Zhang Xiaofei, Zhou Ming, Chen Han,et al. Two-dimensional DOA Estimation for Acoustic Vector-sensor Array Using a Successive MUSIC[J].Multidimensional Systems and Signal Processing,2014,25(3):583-600. [3] 康亚芳,王静,张清泉,等.基于2D-MUSIC算法的DOA估计[J].海南师范大学学报(自然科学版),2014(3):266-270. [4] 张虎,仝侨.基于L型阵的二维Root-MUSIC波达方向估计算法[J].电子科技,2015,28(2):11-13. [5] 杨力强,刘声,杨力生,等.二维ESPRIT类算法中参数配对的新方法[J].无线电工程,2014(11):23-25. [6] 马英英,刘帅,金铭,等.基于数据插值的二维MUSIC谱峰搜索算法[J].现代电子技术,2015(15):35-38. [7] 张远芳,周正,李会勇.极化敏感L型阵模值约束的多参数联合估计[J].雷达科学与技术,2016,14(1):81-85. [8] 张智,姜秋喜,潘继飞,等.基于二维ESPRIT的散射中心建模方法研究[J].电子对抗,2014(1):17-22. [9] 曾浩,张迎辉,冯文江.快速子空间谱峰搜索方法[J].计算机应用,2009,29(9):2546-2547.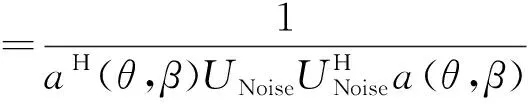
2.2 算法改进
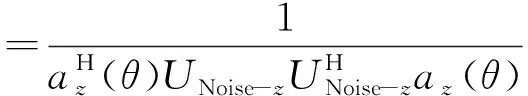


3 算法的有效性与影响因素仿真分析
3.1 算法有效性分析
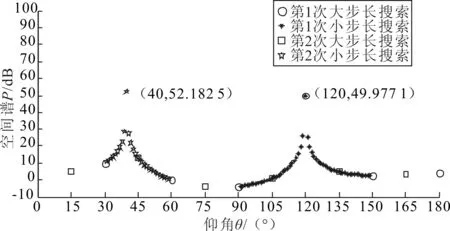
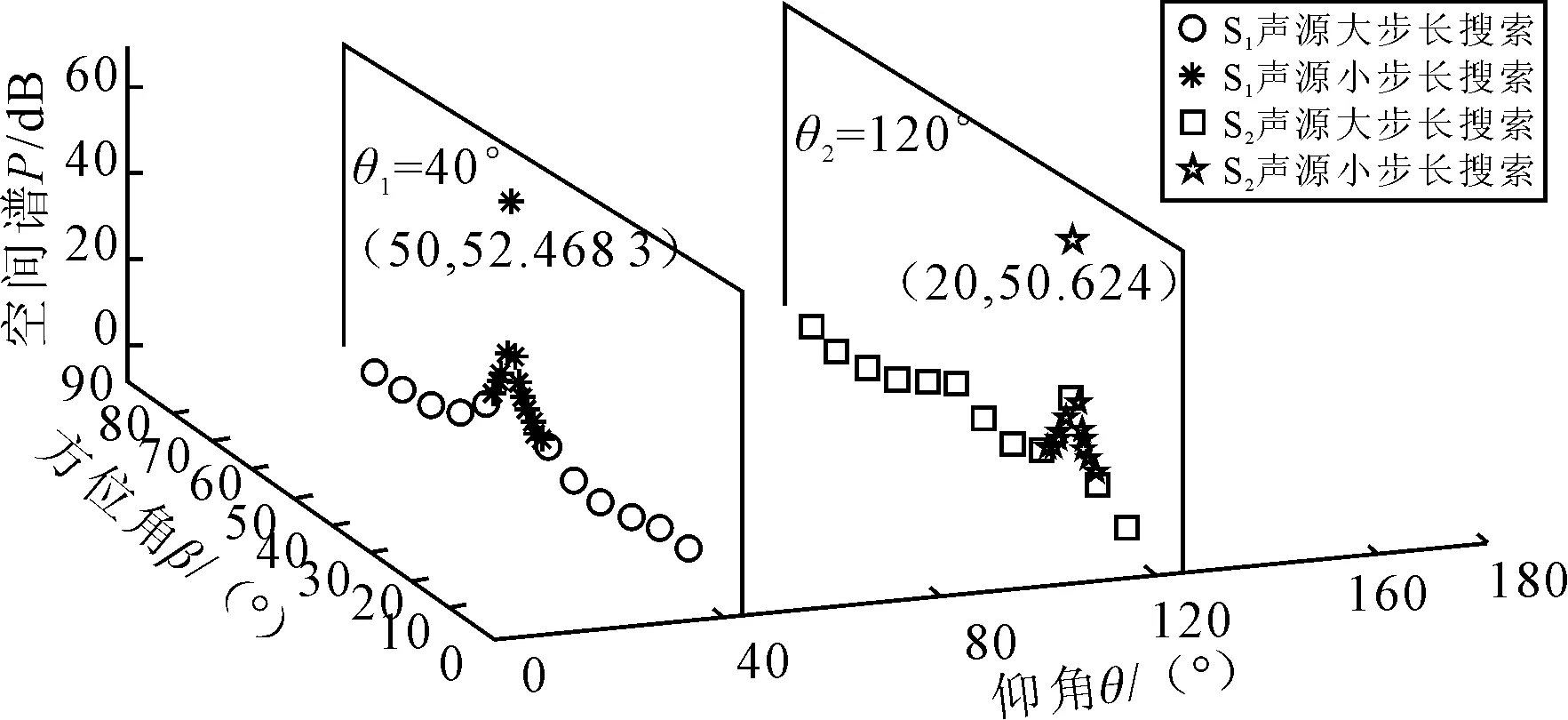
3.2 各信噪比下的估计方差
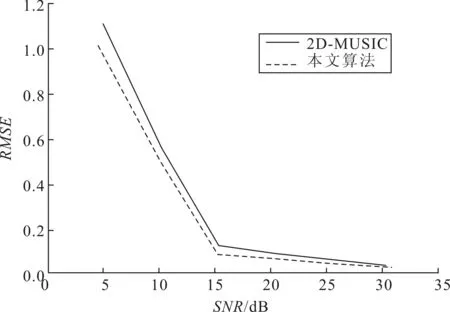
3.3 不同精度下预算耗时

3.4 阵列安装误差的影响

4 工程实用性验证


5 结论
