铅锌矿废石淋滤液在地下水潜水含水层中的迁移模拟研究——基于有限差分法

伍阳，黄鑫，张静，杨利均

(1.四川景星环境科技有限公司,四川成都 610037；2.四川农业大学，四川成都 611130)

地下水埋藏在土壤、岩石的孔隙、裂隙和溶隙中，以各种不同形式的形态存在[1]，全世界的地下水估计总量多达1.5亿立方公里，几乎占地球总水量的十分之一。目前，我国约有70%人口以地下水为主要饮用水源，全国95%以上的农村人饮用地下水，全国40%的耕地使用地下水灌溉[2-3]。它为全球的绝大部分人口提供着水源且支持着农业和工业活动，是一种十分重要的自然资源。然而地下水水质在水环境中十分脆弱，一旦受到污染，不仅危害时间长，并且治理难度很大，因此对地下水污染的预防重要性远大于治理。

金属矿产的开发带来巨大经济与能源效益，但也会出现一系列对环境的负面影响。其中，废石场淋滤液对周围地下水环境的影响尤为突出。铅锌尾矿在降雨作用下形成含有重金属元素的淋滤液，下渗到地下水环境中随着地下水迁移。它在污染地下水环境的同时，带来饮用水源污染风险和对居民健康的危害。通过数值模拟手段定量评估污染物在地下水环境中的迁移规律，对加强矿区监测管理，以及周围水环境的保护有着重要意义。卢晓华[4]通过建立地下水溶质运移模型，对废水处理车间发生泄漏情况下地下水重金属污染情景进行了数值模拟与环境影响预测评价，对环保部门从源头上防治和管理潜在的地下水重金属污染、保护地下水环境具有重要的意义；冯书顺等[5]采用数值方法对矿坑井涌水量进行了预测和模拟；邓鼎兴[6]采用有限元法对矿山地下水污染的分区治理效果进行了数值模拟检验，结果表明数值模拟预测结果与实际监测值较为接近，可为类似矿山地下水污染治理提供借鉴。凭借数值方法，在研究二维以及三维的地下水渗流和污染物的基本迁移的基础之上，国内外还出现了对于考虑污染物的化学反应、生物降解、吸附、衰减等多过程的污染物迁移转化研究[7-9]，以及地下水与地表水耦合[10]、地面沉降与地下水渗流耦合等多场耦合模型[11]。

本文以西部某铅锌矿为研究区域，将研究区域合理概化后，建立地下水水流模型与溶质运移模型。以有限差分方法上游加权法为基础，应用MATLAB软件模拟了废石场在非正常情况下特征污染物Pb离子的迁移结果。模拟结果可以为库区地下水环境评价和治理提供科学依据。

1 研究区域概况

铅锌矿所在的东、北及西侧都以山脊为界，南侧以斯弄多支沟为界，地形起伏，总体呈现西高东低，从西北到东南向海拔高度逐渐减小。该地区受西南支气流、西南季风等大气环流的控制而具有高原亚寒带半干旱季风气候的特点，具有日照充足，空气干燥稀薄，多大风，夏秋多雨，干湿季节分明的主要气候特征。最大年降水量为405.7mm，年平均降水量为352.38mm，最大日降雨量24.2mm，降水主要集中在6～9月，占全年降水的87%；年蒸发量1938.4mm。

铅锌矿位于该区域支沟内，矿区地形坡度大，切割较强烈，沟谷发育且纵坡降大，第四系覆盖严重，水文地质边界条件简单，构成晶屑凝灰岩、角砾凝灰岩、溶结凝灰岩与岩浆岩裂隙含水为主的水文地质单元，属以裂隙含水层为主的矿床。松散堆积物呈条带状分布在沟谷平坦部位，形成汇水谷地；沟谷斜坡上部基岩裸露，中、下部覆盖残坡积层。岩石类型以晶屑凝灰岩、角砾凝灰岩、溶结凝灰岩为主，少量地带出露花岗斑岩、闪长玢岩。因此，区内地下水主要赋存在基岩裂隙中，沟谷为其主要排泄区，地下水与地表水分水岭基本一致，地下水径流途径短，分散排泄，水量贫乏。地表水补给源以大气降水和冰雪融水为主，降水多沿地表径流，少量沿表土、基岩裂隙入渗，最终在排泄基准面溢出。

主要水化学类型包括Ca-Mg-HCO3，pH值介于8.19～8.38之间，地下水矿化度介于414.45～422.62mg/L，属中性偏弱碱性，质软到低矿化淡水，水质状况良好。

2 渗流与溶质迁移数学模型的建立

2.1 水文地质概化模型

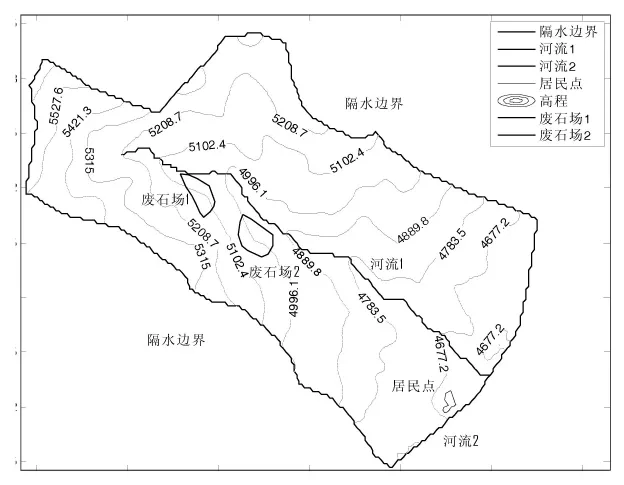
图1 水文模型概念图Fig.1 Concept of hydrological model

研究区内，在天然情况下地下水由西北向东南流动，与河流1平行的两侧分水岭的垂向上几乎无地下水交换，故两侧山脊线可概化为零流量边界。西北处的为海拔较高的地形起伏较大的区域，故选取西北的天然分水岭作为隔水边界线。河流1与河流2所处第四系松散层，加之居民处的水井开采对边界水位几乎无影响，故概化为定水头边界。研究区顶部常年接受降水补给，可概化为潜水面边界。研究区底部主要为为矿体底板，岩层的透水性弱，故概化为隔水边界[12]。

2.2 潜水含水层渗流控制方程

因为本地区岩层倾角平缓，可以把地下水当作平面二维问题。此外，由于受地形起伏控制研究区地下水流场形态较为复杂，地下水以泉水及溢出面形式出露，为此本次计算采用稳定流建模。根据达西定律，对其建立起二维稳定流形式的控制方程[13]：

其中Kx为在横向上的渗透系数，Ky为在纵向上的渗透系数，其单位为m/d。

2.3 污染物迁移控制方程

污染物的迁移主要受到两方面的驱动：一是浓度梯度引起的溶质分子的扩散，其扩散通量与浓度差的关系满足费克定律；二是由于地下水流动引起的机械弥散。溶质运移控制方程[14]：

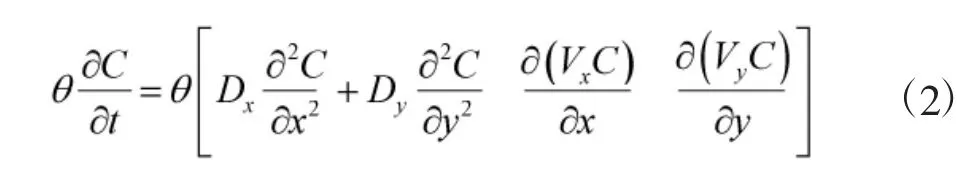
其中θ为含水层有效孔隙率；Dx为横向水动力弥散系数；Dy为纵向水动力弥散系数；Rd为阻滞因子；Vx代表在横向上的地下水流速；Vy代表在纵向上的地下水流速。流速Vx或Vy由达西定律得到：

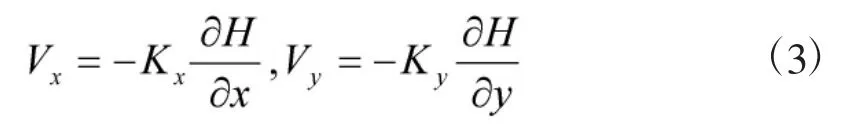
水动力弥散系数包括机械弥散系数与分子扩散系数：

其中V为地下水实际流速，Vx与Vy分别为地下水速度在横向和纵向上的速度分量，Dm为分子扩散系数。

2.4 初始条件与边界条件

在本研究中，地下水渗流场模型中海需要确定的边界条件有第一类边界与第二类边界。

地下水运移的定解条件：

（1）第一类边界条件：地下水渗流方程中的第一类边界为定水头边界，本研究区域中的河流可视为定水头边界：

（2）第二类边界条件：地下水渗流方程中第二类边界为定流量边界，本研究区域中的分水岭为隔水边界，即零流量边界:

溶质运移的定解条件包括了初始条件和边界条件：初始条件：

边界条件：

（3）第一类边界条件：废石浸出液入渗为连续注入式，地下水污染溶质迁移模拟公式参考《多孔介质渗流与污染物迁移数学模型》（仵彦卿编著）一书中平面连续注入示踪剂，一维流动二维弥散模型，污染源连续注入含水层，污染物浓度在各个时刻均为常数：

（4）第二类边界条件：污染物溶质运移的第二类边界为定扩散通量边界，此边界与地下水渗流的第二类边界线重合，则此边界为零扩散通量边界：

3 数值模拟及结果

3.1 有限差分数值解法

有限差分法是一种将微分方程的控制方程及对应定界条件离散，利用迭代法求解出微分方程数值解的方法。地下水流动模型与污染物运移模型是耦合的系统模型，但在稳定流的情况下，可先求出稳定流条件下的流场分布，再根据研究区域内的各个点水头求出速度场，最后根据离散化后的溶质运移差分方程迭代求出污染物随时空变化的浓度值。

本文研究区域为根据自然边界线划分的不规则区域。采用矩形网格剖分方法，共剖分了12334个节点，每个矩形网格大小为30×30m2。由于研究区域被划分为正方形网格且含水层各向同性，即Δx=Δy，Kx=Ky对于地下水渗流方程，其离散后差分格式为[14-15]：

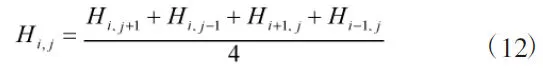
采用上游加权法，得到地下水溶质运移方程的显式差分方程为：

3.2 定解条件的确定

如图1所示，地下水水流模型的隔水边界在整个研究区域的北侧、西侧和南侧，定水头边界为内部河流与东侧边界处河流边界。地下水水流模型的隔水边界为污染物溶质运移的零通量边界。根据2016年地勘资料对研究区域的污染物检测值作为初始浓度即CO=0.02mg/L。

3.3 参数选取

在服务期满(11a)前，认为污染源为连续注入式，即淋滤液通过地表和包气带到达地下水系统后的浓度为常数。其源浓度Cq计算按公式计算[14]：

其中sourceC为污染物下渗漏量[14]:

其中Cp为污染物实验最大浸出液浓度(mg/L)，α降水入渗补给系数，A为废石场渗水面积(m2)，I为降水量(mm)。

废石场中的废水渗透穿过库底后，进入第四系的潜水含水层，漂石含量小于2%，卵石含量40%～55%，卵石最大直径10cm；混杂粘土与砂砾，不均匀。根据项目水文地质勘查报告，评价范围内坡积层孔隙水的渗透系数为5.4m/d。废石场所在区域的潜水含水层都是第四系坡积物、洪积物或冲积物，有效孔隙度取值0.10。采取类比的方法，确定含水层的纵向弥散度为0.3(m2/d)。根据经验公式取横向弥散度为纵向弥散度的0.1倍，即横向弥散度为0.03(m2/d)[16]。将研究区域已有水文资料中的参数作为初始值赋给模型，通过实测的地下水水文位数据与模拟的水文数据进行对比验证，采用经过识别与验证水位后的参数作为模型参数来预测地下水流场与溶质运移。验证后的参数取值见表1。

表1 模拟水文地质参数及取值Tab.1 Chemical characteristics of the tested swine manure before and after leaching

3.4 结果分析

3.4.1 地下水流场分析

以海拔高度表示研究区域内各点的水位高度，稳定流情况下的地下水的水位等值线图见图2。

研究区的地下水流场受该地区的地形控制，一致地呈现出西高东低，由西北向东南递减的规律。内部河流的前半段为河流沟谷，地下水除自西北向东南向流动，还会向内部河流形成的沟谷汇集流动，实现地下水补给地表河流。内部河流后半段的冲积平层，即图2由红色虚线围成三角区域，形成了一个微小的分水岭，它的分流作用使水流不仅仅沿着内部河流向边界河流汇集。此外，边界处的河流流向为自南向北，汇集内部河流后向下游流动，在研究区域内水流最终以边界处的河流下游为出口。

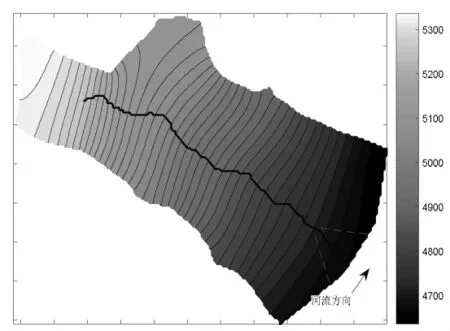
图2 水头等值线图Fig.2 Contour line of water head

研究区域内的水力梯度不大，变化不剧烈，但由于所处区域的岩层渗透系数较大，会由于较强的对流作用使得污染物能够较为快速地随着地下水迁移。另一方面，水流主要流向边界河流，最终沿边界河流的下游方向迁移，使得该区域地下水污染物的不易累积。

3.4.2 污染物迁移规律分析

分别取在1000天、11年（服务期满）、16年（服务期满后5年）、30年后这几个时间节点，得到各时间节点的污染物浓度分布见图3。

在服务期满前，废石场淋滤液被简化为浓度恒定的污染源。污染物在地下水系统中主要受对流作用迁移，沿着地下水主要流动方向由西北向东南方向迁移，同时具有向内部河流形成的河谷汇集的趋势。根据对流场的分析可知，由于靠近边界河流处的扇形冲积平层的分水岭作用，污染物在随着地下水迁移到内部河流下游时将被分散到河流两侧。同时在弥散作用下，在河流2的上游地带部分污染物扩散到了河流2的对侧。由于流速较大同时纵向弥散度较小，所形成的污染羽形状较为扁平。在离污染源最远处的浓度最小，在污染羽中心且靠近源强处的浓度最大，呈现出中心高四周低的规律。

在服务期满后，废石场下渗淋滤液量减少为零。污染物继续沿着地下水主要流动方向迁移，在服务期满前后污染物迁移到达居民点，并且在河流1的下游的污染带宽度逐渐扩大。污染羽仍然呈现出中心浓度高而边缘浓度低的特征。污染物汇入河流1后，随着河流1从南向北向下游迁移，使得研究区域内的污染物不断减小，所形成的污染羽长度逐渐减小，中心也逐步向河流2的下游移动。在30年后，大部分污染物已经流出研究区域，居民点也不再处于污染羽的范围内。污染物在研究区域内总体快速迁移而不滞留。

3.4.3 对居民点的影响

图3 污染物在各时期的浓度分布图Fig.3 Concentration of Pollution in different times

居民点内与整个研究区域内污染物的最大浓度随天数变化规律曲线如图4所示。总体来看，研究区和居民点的最大污染物浓度变化规律较为一致，最大浓度随天数变化曲线形状呈现为宽峰。最初研究区域内的最大浓度为废石场下渗处的源强浓度，随着时间增加最大浓度也增加，在5500天之后区域内的最大浓度达到最大的0.2mg/L，并保持稳定。在8700天左右，区域内的最大浓度开始下降，到10000天左右降低到0.05mg/L度，随着时间增加最大浓度也增加，在5500天之后区域内的最大浓度达到最大的0.2mg/L，并保持稳定。在8700天左右，区域内的最大浓度开始下降，到10000天左右降低到0.05mg/L以下。由于污染物到达居民点需要一定的时间，所以0-3900天居民点内未检测到污染物。3900天后居民点内最大浓度开始随时间上升，在6000天左右达到最大值。居民点内保持该最大浓度到8700天后开始下降，到11000天左右，居民点内无法检出污染物。

图4 研究区与居民区的最大铅离子浓度变化图Fig.4 Maximum concentration of pollution in research area and residence area

居民点铅离子的最大检出浓度为0.0386mg/L。根据GB/T14848-93Ⅲ类水体标准，Pb≤0.05mg/L。居民点内的铅离子浓度未超标。以0.003mg/L的检出限值为标准，污染物到达居民点需要3910天左右。而在研究区域内，大部分时间铅离子浓度超过了0.05mg/L，且最大浓度达到了0.2mg/L。

4 结论

本文根据西藏某铅锌矿的水文地质条件，建立了地下水渗流与废石淋滤液在地下水系统中运移的数学模型，数值结果合理可靠，对于定量化研究地下水污染防治提供理论依据。

（1）研究区域内的水位与高程基本吻合，地下水流场受地形控制，自西北向东南的流动为地下水的主要渗流方向，地下水沿河流1向下游流动，与河流2汇集后向河流2下游流动，有利于污染物的扩散而不累积。

（2）污染物沿着地下水主要流动方向由西北向东南方向迁移，同时具有向内部河流形成的河谷汇集的趋势，当污染物到达河流2后将沿河流2下游方向迁移离开研究区域。整体来看，运移过程中所形成的污染羽形状较为扁平。在离污染源最远处的浓度最小，在污染羽中心且靠近源强处的浓度最大，呈现出中心高四周低的规律。

（3）污染物到达居民点需要约3910天，污染物的最大检出浓度为0.0386mg/L，未超过地下水Ⅲ类水质量标准限值，因此模拟结果表明淋滤液对居民点没有造成风险和危害。但在5000-8000天的时段内，需要加强对敏感点的监测，提前预防可能出现的风险并进行实时相应防治措施。

[1]焦甜,王军霞,唐仲华,等.地下水溶质运移方程有限差分格式的实证研究[J].安全与环境工程,2016,23(3):17-23.

[2]孟展.西藏斯弄多铅锌银矿床矿物学特征研究及地质意义[D].成都理工大学,2016:23-39.

[3]陈华君,胡若鹏,邓竞超.淋滤条件下铅锌尾矿中重金属对环境影响研究[J].云南冶金,2016,45(1):56-63.

[4]卢晓华.基于数值模拟的企业地下水重金属污染的环境影响预测评价[J].安全与环境工程,2014,21(1):93-97.

[5]冯书顺,王国瑞,马自强,等.基于Visual Modflow的矿井涌水量预测模拟研究[J].煤炭技术,2016,35(2):239-242.

[6]邓鼎兴.某矿山地下水污染分区治理效果的数值模拟[J].安全与环境工程,2013,20(4):27-31.

[7]张晓叶.基于可渗透反应格栅的地下水中2，4-二氯酚溶质运移模拟研究[D].北京工业大学,2015,1-2.

[8]焦友军,施小清,吴吉春,等.基于PHT3D的地下水中六价铀吸附反应运移数值模拟[J].地下水,2015(2):8-10.

[9]Salmon S U,Prommer H,Park J,et al.A general reactive transportmodelingframeworkforsimulatingandinterpreting groundwater14Cageandδ13C[J].WaterResourcesResearch,2015,51(1):359-376.

[10]孙骁磊.银北井渠结合灌区地表水地下水耦合模拟及优化配置研究[D].宁夏大学,2016,2-3.

[11]Ahad J M,Ganeshram C L,Bryant L M.,et al.Sources of n-alkanes in an urbanized estuary:Insights from molecular distributions and compound-specific stabl e a nd radiocarbonisotopes[J].MarineChemistry,2011,126(1),239-249.

[12]张人权,等.水文地质学基础(第六版)[M].北京:地质出版社,2011:1-184.

[13]薛禹群,吴吉春.地下水动力学[M].北京:中国水利水电出版社,2009:1.

[14]仵彦卿.多孔介质渗流与污染物迁徙数学模型[M].北京:科学出版社,2012.

[15]薛禹群,谢春红.地下水数值模拟[M].北京:科学出版社,2007.

[16]GelharLW,Welty C,Rehfeldt K R.Reply to Comments on“A critical review of data on field-scale dispersion in aquifers”by S.P.Neuman[J].Water Resources Research,1993,29(6):1867-1869.