几何形体上积分的微元法教学

赵玉娟

（吉林大学数学学院，吉林 长春 130022）

随着现代社会的发展，数学教育的普及和日益广泛的应用，高等数学的用途越来越显露出来。我们在教学中遇到了一个关于微积分的应用问题，通过这个问题，使我们积累了培养学生发现数学问题及培养学生解决问题能力的经验，严谨性与逻辑性的关系，以及解决实际问题过程中的全面性。尤其是边界问题，极值问题与最值问题等的实际意义。

一、问题

1、我们把具有长度，面积，体积等形状的物体统称为几何形体。几何形体上的积分就是指多元函数的积分域是具有几何形状的物体上（包括曲线，曲面，区域，立体等）。其方法就是利用微元法。先化整为零，再“积零为整”。即把“大化小”，求出小几何形体的度量，并把它看做一个“点”，这个点仍具有小度量的意义，再对这些“点”求和，即对几何形体上求积分。具体方法如下：

2.举例

当几何形体为空间区域时，我们计算质点绕定轴转动的转动惯量问题。

例1设密度为常数ρ，底面半径为R，厚度为常数h的圆柱立体，圆柱体的轴向上有4个螺母形“空柱”，分布于直径上相互垂直的位置上，空柱半径为求这个有“洞孔”（如图2）且底面半径为R，厚度为常数h圆柱绕其中心轴旋转的转动惯量，并讨论转动惯量何时最大。

解：首先建立空间直角坐标系，以旋转轴为oz轴，以底面为oxy面，以底面圆形中心为坐标原点建立直角

转动惯量I=m r2;其中r是质点到旋转轴的垂直距离，m是物体质量。当几何形体的形状为G时，其绕定轴L旋转时的转动惯量

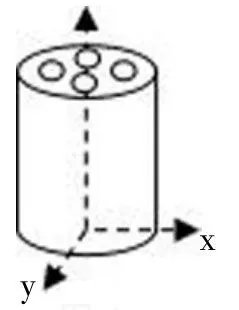
图1

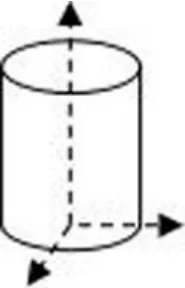
图2

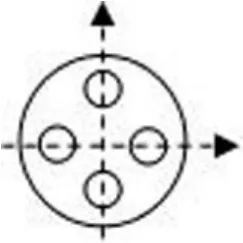
图3

图4

其中r表示dG（看做点）到旋转轴L的垂直距离，ρ表示几何形体G的密度，dG表示几何形体的度量（几何形体的长度，面积，体积等总称为几何形体的度量）。

（1）先计算实心圆柱（如图2）绕其中心轴（oz轴）旋转的转动惯量。

根据微元法，设在 oxy 面上，底面所占区域 D1=｛（x，y）│x2+y2≤R2}，在D1上点 (x,y)处，取一小块平面区域，记为 dσ，也用它表示面积；柱体上与dσ对应的空间区域用dG表示，同时也用它表示体积dG=hdσ，则，把dG看做点(x,y,z)处的质点，则dG其绕中心轴oz轴旋转时的转动惯量；dI=r2dm=（x2+y2）ρhdσ；计算出转动惯量

（2）设“空柱”的轴心位于距离整个柱体轴心a处，半径为在底面上(在 oxy面上)位于点（a，0）处（参考图 3），a满足，取令则计算出此“空柱”部分的转动惯量

利用积分区域的可加性，积分的轮换对称性及转动惯量的可加性，并利用（1）的结果，故有4个小圆“洞孔”的圆柱绕中心轴oz轴旋转的转动惯量为

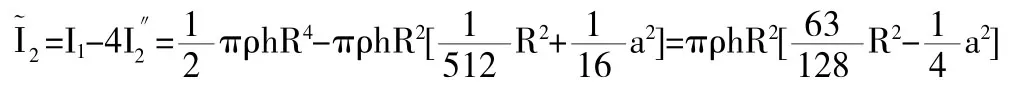
其中带有4个圆“洞孔”柱的立体质量为m2=ρh[πR2-4π代入上式得

例2设密度为常数ρ，底面半径为R，厚度为常数h的圆柱立体，圆柱体的其轴向上有4个扇形“空柱”，分布于直径上相互垂直的位置上，扇形空柱半径为，求这个有“洞孔”（如图2）且底面半径为R，厚度为常数h圆柱绕其中心轴旋转的转动惯量，并讨论小扇形孔位于底面何处时转动惯量最大，并与例1中的结果比较那种形状的圆柱体转动惯量更大。

解：画出底面形状在oxy面上图形（如图4），实心柱绕其中心轴的转动惯量为

设扇形的顶点在（a，0）时，其中，先计算出圆柱上位于小扇形“洞孔”处的相应部分绕oz轴的转动惯量，由于在oxy面上，顶角为

根据积分区域可加性和积分的轮换对称性及转动惯量的可加性，并利用（1）的结果，故得有4个形状相同的小扇形“洞孔”的圆柱绕中心轴oz轴旋转的转动惯量

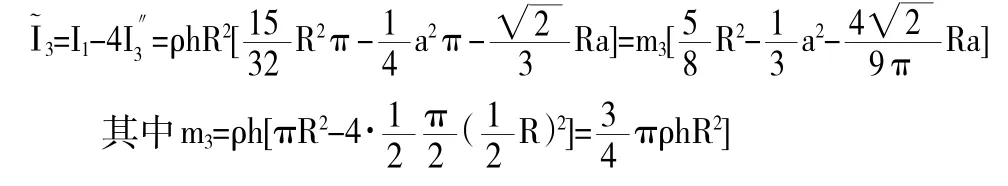
二、结果的对比分析

（1）取时，得若R为常数，假设几种不同形状的圆柱体的质量相等，即m1=m2=m3时，显然I1＜I2且I1＜I3，即实心柱的转动惯量I1最小。

（3）讨论对于“孔洞”为扇形柱的柱体（底面图形如图4），

图5

图6

图7

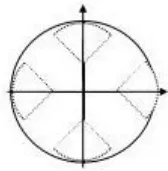
图8

其转动惯量可疑的极值点为，因为0＜a＜R，所以函数无极值。而a的值越大，转动惯量就越小；a的值越小，转动惯量也就也越大。当a=0时，转动惯量最大，此时圆柱体是一个空心柱。（图7）；当时，最小，此时“洞孔”圆柱与外缘相切（图8）。

（4）对于例1的最小值和例2的最小值

这只是一个数学的应用问题，是微积分的数学应用教学。

在实践教学中，我们一方面，要教会学生使用微元法，另一方面，要教会学生结合具体问题建立数学模型，这个模型其本质上是高等数学中极值和最值问题。尤其是要注意的是边界情况，要结合实际问题说明边界点的重要性。慢慢培养学生严谨性，这对学生的数学素质提高是极好的训练。

三、数学模型教学的现实意义

通过上述模型的研究，显示出多元微积分学应用的重要性。

我们通过这个例题培养学生发现数学问题，并用所学的知识解决问题的能力，了解数学问题遍布生活的方方面面，只要你能注意到问题的存在，这对培养创新型人才具有现实意义。在高等数学教学中我们教给他们一些建模方法，对他们后续课程和未来的工作都是有益的，所谓厚积薄发。使学生了解数学不是抽象得离生活很远。及早培养学生用数学方法解决实际问题的意识，数学是当今时代必要的技术手段，学会用数学手段解决问题，是科学未来发展的必要基础。

[1]赵玉娟等.知识经济时代的数学教学[J].现代教育科学，2004,（12）.

[2]COMAP（申大维等译）.数学的原理与实践[M].高等教育出版社,施普林格出版社，2004.