基于并行交叉遗传粒子群算法的水文频率参数估计

佘 纬，夏永波

(中南民族大学 数学与统计学学院，武汉 430074)

水文设计值是各种水利工程建设的依据，它是通过现有的水文资料进行水文频率参数估计从而推求出来的.在中国广泛采用的理论频率分布线型是P-Ⅲ型分布，因此P-Ⅲ型分布的参数估计吸引了很多学者的注意.多年来，水文工作者们对水文频率参数估计问题做了大量的研究工作，提出了适线法、矩法、权函数法、概率权重矩法和线性矩法等.适线法(配线法)一直是我国估计水文频率曲线参数的主要方法，分为目估适线法和优化适线法两类.目估适线法又称经验适线法，是寻找一组参数，使这组参数所决定的理论曲线与经验点据拟合最优[1].但是使用不同的适线准则和不同的经验频率计算公式得到的结果差异很大，计算结果对个别异常点十分敏感，从而导致所配曲线受少数异常点控制，时常偏离大多数经验点的分布，只有一个积累了丰富经验的工程师，才有可能用经验适线方法做出精确的计算，但是水文频率计算作为一门科学，不能永远停留在凭经验计算上.计算机优化适线法采用智能算法对参数进行迭代寻优，参数估计精度高，因此是现今广泛使用的水文频率参数估计方法.矩法属于单参估计，不能全面确定P-Ⅲ型频率曲线的参数估计问题[2].权函数法的计算精度相对于矩法有了提高，但其计算复杂[3].概率权重矩法和线性矩法避免了计算中的高次方，在无偏性和有效性方面都优于一般的矩法和权函数法[4]，但是矩法、权函数法、概率权重矩法和线性矩法都是计算步骤固定的没有自适应能力的参数估计方法，对于不同的样本，其参数估计精度不同[5].因为优化适线法所表现出的优点，其成为了国内外学者们研究的热点，文献[6]将采用SCEM-UA优化算法的适线法和矩法、权函数法、概率权重矩法进行了比较，验证了优化适线法的优势；文献[7]研究发现，当参数数目较多且取值范围较大时，PSO算法比SCE算法更高效；文献[8]将PSO和GA算法相结合，设计了混合粒子群算法来进行水文频率参数估计；文献[9]讨论了粒子群初始化对PSO算法性能的影响；文献[10]将PSO算法的局部搜索中增加了新的更新机制，从而提高了算法的性能；文献[11]通过构造新的惯性权重和加速系数对PSO算法进行了改进；文献[12]采用精英保留策略增强了遗传算法寻优的精度.本文深入研究了PSO和GA两种算法，提出了并行交叉遗传粒子群算法(PCGA-PSO)，并将其用于水文频率参数估计.

1 P-Ⅲ型分布

P-Ⅲ型分布的概率密度可以表示为：

(1)

其中a0表示水文变量的最小值，α和β为两个重要的参数.Γ(α)是伽马函数，可以表示为：

(2)

因为水文变量不可能为负值，所以a0≥0；一般情况下，水文变量不可能太大或太小，所以根据水文工作者的经验，取α>1,β>0.式(1)的几个数字特征可以表示为：

(3)

(4)

(5)

式(3)描述了水文随机变量的数学期望E(x).CV为变差系数，CS为离差系数，分别用式(4)、(5)进行描述.从式(3)～(5)可以看出，若已知E(x)、CV和CS，便可以求得式(1)中三个重要参数a0，α和β，经推导得到：

(6)

(7)

(8)

根据水文频率的实际数据和实际分析经验，对变差系数和离差系数的取值，有如下约束：

(9)

其中kmin=xmin/E(x)，xmin为水文变量的最小值.

在水文频率计算中，一般需求出指定频率p所对应的设计值xp，这要通过对密度曲线进行积分，求出等于或大于xp的累积频率p值，即：

(10)

2 适线法步骤

适线法的步骤如下.

步骤1：由估算的E(x)计算kmin，再根据式(9)决定CV和CS的取值范围；

步骤2：选择适线方法；

步骤3：根据式(11)或式(12)表示的适线准则进行适线；

(11)

(12)

其中，Δxi为实际水文数据点和理论频率曲线之间的偏差，δ1为离差绝对值和，δ2为离差平方和.

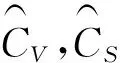
步骤6：将a0，α和β代入式(10)，求得相应于xp的累积频率p值.

3 并行交叉遗传粒子群算法

基于GA和PSO算法的优缺点，本文提出了PCGA-PSO算法，该算法在初始种群的产生与编码、GA和PSO的执行方式和数据融合、PSO算法的惯性权重等方面进行了改进和设计.

3.1 初始种群的产生和编码

PCGA-PSO算法采用十进制编码，设初始种群的取值范围为[a，b]，其产生初始种群的步骤如下：

(i) 将区间[a,b]划分为M个小区间；

(ii) 在每个小区间随机产生两个数，分别记为Qi，Pi，i=1,2,…,M；

(iii) 将Q1,Q2,…，QM作为GA算法的初始种群，P1,P2,…，PM作为PSO算法的初始种群.

3.2 GA和PSO的执行方式和数据融合

在PCGA-PSO算法的执行阶段，令GA和PSO算法并行执行，每隔5代进行一次数据融合，充分发挥GA全局搜索能力强和PSO局部搜索能力强的优点，其具体执行步骤如下：

(1)令GA算法以Q1,Q2,…，QM为初始种群开始执行，PSO算法以P1,P2,…，PM为初始种群开始执行；

(2)执行5代之后，分别计算两种算法得到的新种群对应的适应度值；若满足算法的终止条件，则算法终止；否则，继续下面的步骤；

(3)对两种算法得到的新种群，按照其适应度值降序排序，GA算法的新种群排序之后可记为：R1,R2,…，RM,PSO算法的新种群排序之后可记为：S1,S2,…，SM；

(4) 将SM-k+1,SM-k+2,…，SM和R1,R2,…，Rk进行交换，交换之后，令SM-k+1,SM-k+2,…，SM,Rk+1,Rk+2,…，RM作为GA算法的新种群，令S1,S2,…，SM-k,R1,R2,…，Rk作为PSO算法的新种群，k取1到M/2之间的随机整数；

(5)转到步骤(2)执行.

3.3 PCGA-PSO算法的惯性权重

PSO算法的惯性权重体现了粒子继承先前速度的能力，较大的惯性权重有利于全局搜索，较小的惯性权重则有利于局部搜索.本文实现的是并行交叉GA-PSO算法，在其中的PSO算法部分，根据下列步骤设置惯性权重：

(1)设置初始的惯性权重为：

(13)

根据经验设置初始惯性权重ωstart=0.9，迭代最大次数时的惯性权重ωend=0.4，k为当前迭代次数，Tmax为最大迭代次数.

(2)若最佳适应度值连续3代不变，则令ω(k)=ωstart=0.9，令其向更广的范围探索，若连续3代探索之后，其最佳适应度值仍然不变，则令ω(k)=ωend=0.4，令其深度探索，若最佳适应度值在变化，则采用步骤(1)中的惯性权重；

(3)反复执行步骤(1)、(2)直至算法终止.

3.4 PCGA-PSO算法性能分析

根据3.1、3.2和3.3描述的PCGA-PSO算法，总结其性能特点如下：

(1)PCGA-PSO算法所采用的初始种群产生和编码方法，可以保证初始种群覆盖整个定义域；

(2)PCGA-PSO算法所采用的GA和PSO的并行交叉执行方式，一方面兼顾了算法的局部搜索能力和全局搜索能力，另一方面保证了数据的交叉融合；

(3)对PSO算法惯性权重的设置保证了PSO算法不会陷入局部最优，令其兼顾广度和深度的搜索；

为了验证PCGA-PSO算法的性能，本文使用某水文站的年径流量数据，用PCGA-PSO算法对其进行水文频率分析.

4 实验与结果分析

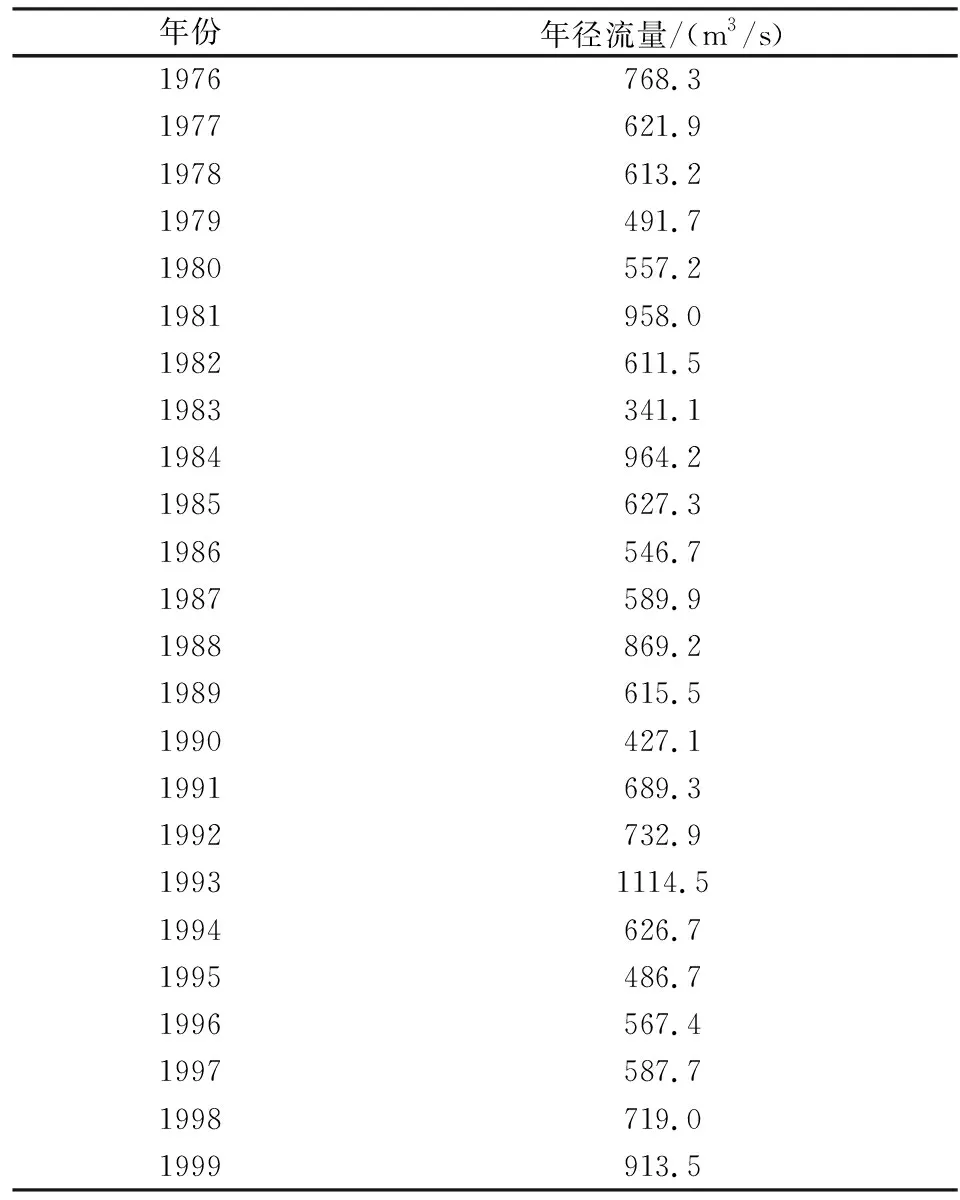
表1 某水文站24年年径流量Tab.1 Annual runoff data of a hydrologic station(24 years)

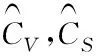
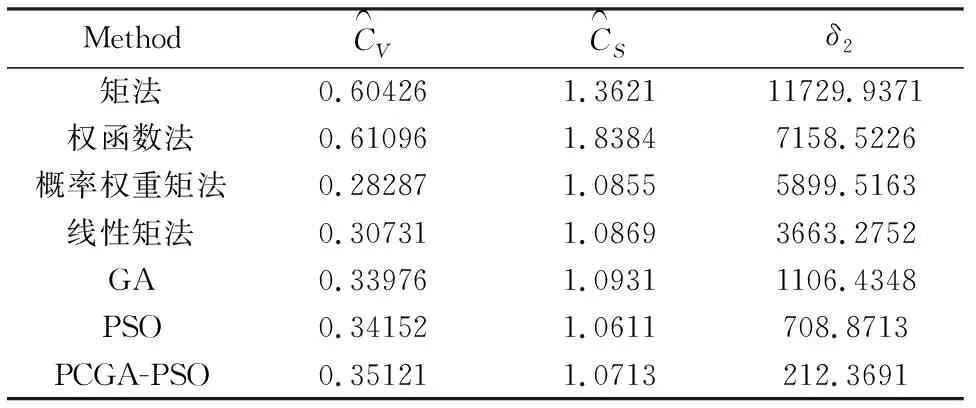
MethodC︵VC︵Sδ2矩法0.604261.362111729.9371权函数法0.610961.83847158.5226概率权重矩法0.282871.08555899.5163线性矩法0.307311.08693663.2752GA0.339761.09311106.4348PSO0.341521.0611708.8713PCGA-PSO0.351211.0713212.3691

图1为利用PCGA-PSO算法得到的水文站的水文频率曲线，可以看出基于PCGA-PSO算法的优化适线法可以很好地拟合实测数据.

图1 基于PCGA-PSO算法的水文频率曲线Fig.1 Hydrologic frequency curve based on PCGA-PSO algorithm

5 结论

本文提出的PCGA-PSO算法对传统算法在3个方面进行了改进.首先，种群的初始化覆盖了个体取值的整个定义域；其次，并行交叉的GA和PSO算法执行方式兼顾了局部搜索和全局搜索，同时还实现了数据融合；最后，PSO算法的惯性权重的取值保证了算法可以及时跳出局部最优，提高其收敛速度.实验表明：PCGA-PSO算法可以有效地进行水文频率参数估计，并为水文数据拟合理论频率曲线，且该算法较传统的数学方法和优化适线法精确度更高.

参 考 文 献

[1] 张炳蔚，何文亮，周 冲. P-Ⅲ分布求矩适线法MATLAB实现与北海海域设计波高估计[J]. 水利与建筑工程学报，2013(5):27-31.

[2] Huang Zhenping,Lin Xiaoli,Hou Yunqing. Moment estimation for parameters of Pearson Type-Ⅲ distribution and calculated frequency of design flood[J]. Journal of Hohai University (Natural Sciences),2005, 33(1):49-51.

[3] Chen Wangchun, Zhao Lifeng. Application of weight function method to P-Ⅲ distribution[J]. Zhejiang Hydrotechnics, 2002(4):46-47.

[4] Yuan Xiuhong. Estimation methods of P-III distribution parameter based on partial probability weighted moments[J].Yangtze River, 2015, 46(13):25-28.

[5] Bai Li,Xia Letian,Wei Yuhua. L-moment method for the Pearson Type-Ⅲ distribution and its expected probability in parameter estimation[J]. Advances in Science and Technology of Water Resources,2008, 28(5):29-31.

[6] 陈南祥，甘 甜，杜青辉. SCEM-UA优化算法在水文频率分析中的应用[J]. 西北农林科技大学学报(自然科学版)，2011(8):210-214.

[7] Tada T. Parameter optimization of hydrological model using the PSO algorithm[J]. Suimon Mizu Shigen Gakkaishi Journal of Japan Society of Hydrology and Water Resources, 2007,20(5):450-461.

[8] 唐 颖，张永祥，王 昊，等. 基于PSO-AGA的水文频率参数优化算法[J]. 北京工业大学学报，2016, 42(6):953-960.

[9] Cazzaniga P, Nobile M S, Besozzi D. The impact of particles initialization in PSO: Parameter estimation as a case in point[C]//IEEE. Computational Intelligence in Bioinformatics and Computational Biology. Niagara Falls: IEEE, 2015:1-8.

[10] Jakubcová M, Máca P, Pech P. Parameter estimation in rainfall-runoff modelling using distributed versions of Particle Swarm Optimization Algorithm[J]. Mathematical Problems in Engineering, 2015, 2015:1-13.

[11] 谭 貌，段 斌，周 啸，等. 基于改进PSO的中厚板轧制规程能量优化设计[J]. 中南大学学报(自然科学版)，2014(5):1476-1483.

[12] 刘 健，李京航，柏小丽. 基于精英保留策略遗传算法的配电网无功优化[J]. 电气技术，2015(4):35-38.