带奇异项的拟线性抛物方程组在第二类边界条件下解的猝灭

孙仁斌

(中南民族大学 数学与统计学学院，武汉 430074)

本文考虑如下带奇异项的拟线性抛物方程组在第二边界条件下的初边值问题：

(1)

H1：μ(x,t),υ(x,t)为非负有界连续函数，0≤μ(x,t)≤μ0,0≤υ(x,t)≤υ0.

H2：φ(s),ψ(s)为非负连续可微函数，且φ(0)=ψ(0)=0；当s>0时，φ′(s)>0，ψ′(s)>0.

对于抛物型方程和方程组解的猝灭现象的研究，最早由Kawarada提出，早期的工作都是针对单个函数的半线性方程展开讨论[1-6]，随着研究的深入，两个函数的半线性抛物方程组也引起人们的关注[7-9]；另一方面，讨论的方程和方程组的复杂程度也在增加，由半线性方程转向退缩的拟线性方程和方程组[10-15]，大部分的结果都是针对第一边界问题的，而对于第二边界条件下的初边值问题的讨论却很少见．本文讨论的问题(1)中，由于有条件H2，方程出现退化，而且退缩项由更具一般性的函数φ(s),ψ(s)构成，讨论起来难度更大，边界条件也与大部分已有文献中的类型不同，属于第二类．本文的主要结论是问题(1)的解在一定条件下会在有限时刻发生猝灭，得到此结论用到的主要是上下解方法，为此，先介绍与此类方程有关的上下解的定义、比较原理及解的存在性，再通过构造问题(1)的一个下解来得到本文的结论．

1 比较原理与解的存在性

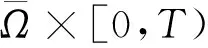
(2)

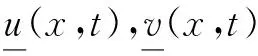
利用与文[16]、[17]中类似的方法，可以得到下面的比较原理和解的存在性定理.

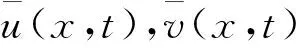
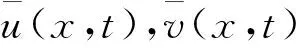
考虑常微分方程组：

(3)

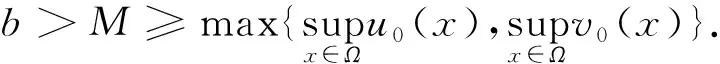
按照上解的定义，定理3的证明是很容易完成的，在此省略. 因此，如果能找到问题(1)的一个下解，则由定理2，问题(1)的解一定存在，我们将在下段完成下解的构造并得到本文的主要结论.

2 解的猝灭性

考虑边值问题：

(4)

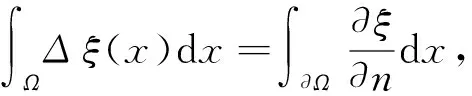
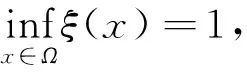
1≤ξ(x)≤K,x∈Ω.

(5)

为了得到问题(1)的下解，我们还需要另一个结论.

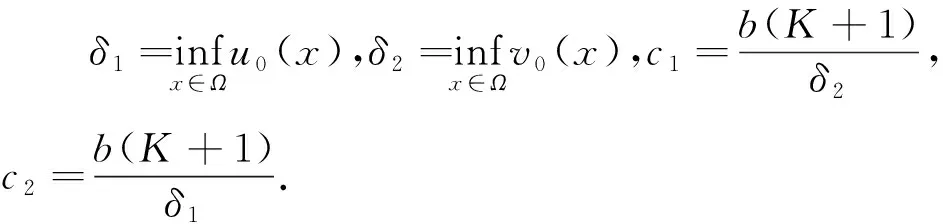
设常数b,p,q及区域Ω的测度之间满足：

(6)

又令：

(7)

(8)

引理1 假设(6)式成立，则m1>0,m2>0．

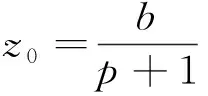
取常数l1,l2满足：

(9)

构造函数：

(10)

(11)

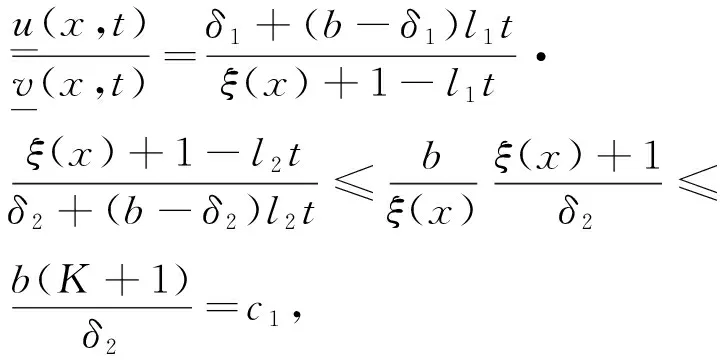
证明直接计算有：

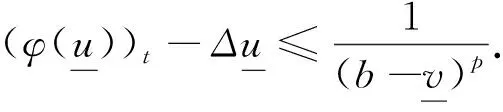
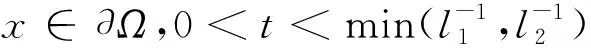
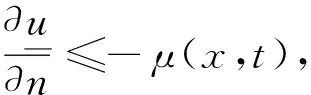
综合定理2～4的结论，可以得到本文的主要结果----定理5．

定理5 设μ0≤δ1,υ0≤δ2，则问题(1)的解必在有限时刻发生猝灭．

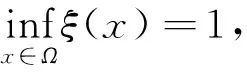
参 考 文 献

[1] Chang C Y，Chen C S． A numerical method for semilinear singular parabolic quenching problems[J]. Quarterly of Applied Mathematics，1989, 47:45-57．

[2] Guo J S．On the quenching behavior of the solution of a semilinear parabolic equation[J]． Journal of Mathematical Analysis and Applications，1990, 151:58-79．

[3] Dai Q Y，Gu Y G．A short note on quenching phenomena for semilinear parabolic equations[J].Journal of Differential Equations, 1997, 137:240-250．

[4] Dai Q Y，Zeng X Z．The quenching phenomena for the Cauchy problem of semilinear parabolic equations[J]. Journal of Differential Equations，2001, 175:163-174．

[5] Salin T．On quenching with logarithmic singularity[J].Nonlinear Analysis,2003,52:261-289．

[6] Zhi Y H，Mu C L，Yuan D M．The quenching phenomenon of a nonlocal semilinear heat equation with a weak singularity[J]．Applied Mathematics and Computation，2008，201:701-709．

[7] 戴求亿．半线性抛物方程组的死灭现象II[J]．应用数学学报，1997，20(1):11-23．

[8] Zheng S N, Wang W．Non-simultaneous versus simultaneous quenching in a coupled nonlinear parabolic system[J]．Nonlinear Analysis, 2008,69:2274-2285．

[9] 孙仁斌．含有奇异项的退缩抛物方程解的整体存在性与有限时刻猝灭性[J]．中南民族大学学报(自然科学版)，2013，32(1):102-105．

[10] Winkler M．Quenching phenomena in strongly degenerate diffusion equations with strong absorption[J]. Journal of Mathematical Analysis and Applications，2003,288:481-504．

[11] Giacomoni J，Sauvy P，Shmarev S．Complete quenching for a quasilinear parabolic equation[J]．Journal of Mathematical Analysis and Applications, 2014,410:607-624．

[12] Zhou M J，Wang C P，Nie Y Y．Quenching of solutions to a class of semilinear parabolic equations with boundary degeneracy[J]．Journal of Mathematical Analysis and Applications, 2015,421:59-74．

[13] Jong-shenq G,Yoshihisa M,Shoji Y. Self-similar solutions for a quenching problem with spatially dependent nonlinearity[J]. Journal Nonlinear Analysis, 2016,147:45-62．

[14] Dao N A,Diaz J I．A gradient estimate to a degenerate parabolic equation with a singular absorption term: The global quenching phenomena[J]．Journal of Mathematical Analysis and Applications, 2016,437:445-473．

[15] Kavallaris N I, Lacey A A, Nikolopoulos C V．On the quenching of a nonlocal parabolic problem arising in electrostatic MEMS control[J]．Nonlinear Analysis, 2016,138:189-206．

[16] Pao C V．Quasilinear parabolic and elliptic equations with nonlinear boundary conditions[J]．Nonlinear Analysis, 2007，66:639-662．

[17] Pao C V．Quasilinear parabolic and elliptic systems with mixed quasimonotone functions[J]. Journal of Differential Equations，2013, 255:1515-1553．