一种基于多目标优化的卫星周期性持续观测任务规划方法

王凌峰,陈兆荣,陈 浩,陈宏盛

1(国防科学技术大学 电子科学与工程学院 信息工程系,长沙 410073)

2(95874部队,南京 210022)

1 引 言

随着航天科技的不断发展,对地观测卫星(Earth Observing Satellite,EOS)已成为获取遥感数据的重要航天资源,在农业、气象、军事、科学研究等领域都起到了重要作用[1,2].为了更好地使用对地观测卫星对地面目标进行有计划的观测,需要根据卫星的能力制定优化卫星观测方案,确定卫星载荷开关机时间及载荷工作模式.

对地观测卫星通常运行在预先设定的固定轨道上,卫星对地观测过程受到能量、存储、姿态调整等约束限制,难以保证所有观测任务都能够被响应.各应用部门日益增加的遥感数据获取需求与卫星有限观测能力之间的矛盾日益突出.卫星任务规划就是要从待观测任务集合中挑选一个子集,在满足卫星约束的同时,使得观测效益最大化.卫星观测任务规划已被证明是一个典型的NP-hard问题[3,4],过载规划特性明显.为了充分利用宝贵的卫星资源,卫星观测任务规划问题得到了国内外学者的高度关注,涌现出了大量研究工作.

Chen Y等[5]提出了一种求解多星任务规划问题的演化学习型蚁群算法,在优化过程中不断抽取构件知识用来指导后续优化;Wei J等[6]建立了卫星任务协同规划模型,在一种基于遗传禁忌选择的求解算法基础上提出协同进化模型的求解技术;Wang J等[7]针对任务动态提交,任务数量和提交时间的不确定性,建立了卫星动态实时规划的多目标模型;Chen H等[8]综合考虑卫星的观测任务和数据传输任务规划,构建了卫星观测任务和数据传输任务联合规划模型,提出了一种基于遗传算法的算法求解;Wang C等[9]将基于案例的学习方法引入到调度过程,考虑类似的历史调度方案,提出了一种基于案例学习和遗传算法的算法.

上述工作中,均假设一旦地面目标被卫星观测,则该任务完成.但随着遥感数据应用的不断深入,逐渐出现了带有时间分辨率要求的对地观测需求.即要求多颗对地观测卫星组成的星群对同一地面目标进行周期性连续观测,以便定期刷新地面目标态势.上述对地观测需求的出现,为卫星任务规划带来了新的挑战,如观测周期较目标要求的观测时间分辨率过大,会导致目标态势刷新不及时;而观测周期太小,又会导致宝贵的卫星资源被浪费.所以,卫星周期性持续观测任务规划问题表现出了明显的多目标优化特性.

论文首先对卫星周期性持续观测任务规划问题进行了描述与分析,建立了数学规划模型,提出了基于多目标分解进化算法的卫星周期性持续观测任务规划方法进行求解,最后通过实验验证了算法的可行性和有效性.

2 卫星周期性持续观测任务规划问题

对地观测卫星绕地球飞行,运行在固定轨道上,当卫星飞行至地面目标上空可视范围内(可视时间窗),星载传感器开机,完成对目标一次观测.卫星只能在若干离散的可视时间窗内对目标进行观测.

多颗对地观测卫星分布在若干预先设定的轨道面上,位于同一轨道面上的多颗卫星之间存在固定相位差,从而组网形成对地观测卫星群.于是,星群中成员卫星可通过多星接力方式对地面目标实施周期性观测,不断获得观测数据,从而实现目标态势定期刷新.目标的观测周期要求称为观测时间分辨率.调度的目的就是针对每一个有观测时间分辨率的地面观测任务,合理优化地安排一系列卫星在适当的可视时间窗对其进行观测,使得观测时间分辨率满足程度最大化,且卫星能耗尽可能小.

我们拟构建约束满足问题(Constraint Satisfaction Problem,CSP)模型,首先给出相关形式化描述.

2.1 问题建模

卫星周期观测调度问题可形式化描述如下:

(a)任务规划时段.规定规划时段T=[TB,TE],TB为规划开始时间,TE为规划结束时间.卫星所有活动须在此规划时段内进行.

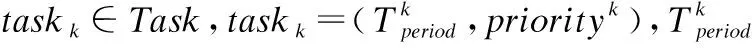
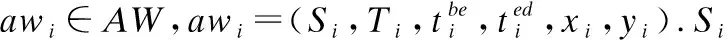
2.2 约束模型

卫星绕地球飞行,执行对地观测任务,由于运行轨道、载荷能力、卫星能量等限制,需要考虑的约束较多.本文主要考虑如下约束:

(a)两次开机时间最短时间间隔约束.星载传感器关机之后,必须经过一段时间才能再次开机.

∀satk∈Sat,∀awi∈AW_DO_Satk,

(1)

(b)单次开机时间约束.星载传感器单次开机时间不能低于单次最短开机时间,且不能长于单次最长开机时间.

∀satk∈Sat,∀awi∈AW_DO_Satk,

(2)

(c)单圈最长开机时间约束.星载传感器单圈累积开机时间不能大于单圈最长开机时间.

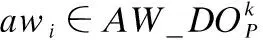
(3)

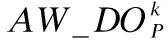
(d)单天最大开机次数约束.传感器单天累计开机次数不能大于单天最大开机次数.

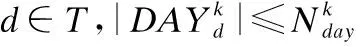
(4)

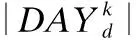
2.3 目标函数

基于卫星运行实际业务需求,本文主要考虑以下两个优化目标:

1)方案总超时程度(the Degree of Timeout,DT):对于每个观测任务,在规划时间段内的两次开机间隔均小于任务时间分辨率,则任务完成;若两次开机时间大于时间分辨率,超出时间称为超时时间.我们定义目标在任务规划时间段内累计超时时间与规划时间长度的比值称为该任务的超时程度.方案中每个任务的超时程度用任务优先级加权平均得到方案总超时程度.

∀satk∈Sat,∀awi∈AW_DO_Taskk,

(5)

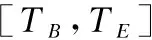
(6)

方案总超时程度:

(7)

2)卫星资源消耗(Resource Consumption,RC):卫星在执行观测任务时会消耗能源、存储容量等资源,我们考虑用卫星使用时间来衡量卫星资源的消耗,使用时间越长资源的消耗越多,并用卫星访问窗口的总时长进行归一化,表示方案对卫星观测资源的使用程度.

(8)

3 卫星周期性持续观测任务规划方法

考虑单个优化目标的卫星对地观测任务规划问题是典型的NP-Hard问题[10].我们考虑了方案总超时程度和资源消耗两个优化目标,求解难度不会低于单目标优化问题.如果采用完全搜索算法进行求解,当问题规模较大时,有效时间内将很难给出可行解.所以,我们拟选用基于多目标分解进化算法的卫星周期性持续观测任务规划方法进行求解.

基于分解的多目标进化算法(MOEA/D)是由Zhang Q等[11]提出的,算法将多目标优化问题分解转化为多个单目标优化子问题,并认为每个子问题对相邻的子问题有指导作用,分别对每一个子问题进行求解,最终得到原优化问题的Pareto最优解.

由于遗传算法具有良好的全局搜索能力,具有内在并行性,适合求解多目标优化问题[12].并且MEOA/D算法的进化计算部分能够直接应用单目标遗传算法,理论分析表明其计算复杂度比NSGA-II算法低[13].该算法已应用于近空通信系统部署优化[14]、作业车间调度问题[15]、天线设计[16]等领域,取得了较好的计算效果.

我们采用MOEA/D算法框架,提出基于多目标分解进化算法的卫星周期性持续观测任务规划方法(Satellite Periodic Continuous Observing Scheduling Multi-objective Optimization Algorithm Based on Decomposition,SPCOSM).

3.1 算法流程图

SPCOSM算法的流程图如图1所示.

3.2 关键算子设计

3.2.1 问题编码

我们采用等长二进制编码方式来构造染色体,决策变量采用观测窗口的使用标志.将参与规划的访问时间窗口按照开始时间先后排序,取出每一个访问时间窗口的使用标志,组合得到一个解:

X=(x1,x2,…,xi,…,xKall).

(9)

3.2.2 种群初始化

算法需要初始化参考点z*=(inf,inf);初始化权向量,生成N个均匀分布的权向量λ1,λ2,…,λN,对应得到N个子问题;初始化进化种群P,随机生成规模为N的进化种群P.

图1 SPCOSM算法流程图Fig.1 Flow diagram of SPCOSM

3.2.3 交叉算子

如图2所示,我们采用单点交叉算子,在种群中依概率选择两个父代个体,并随机确定一个交叉点,互换交叉点后的基因序列,实现交叉过程.

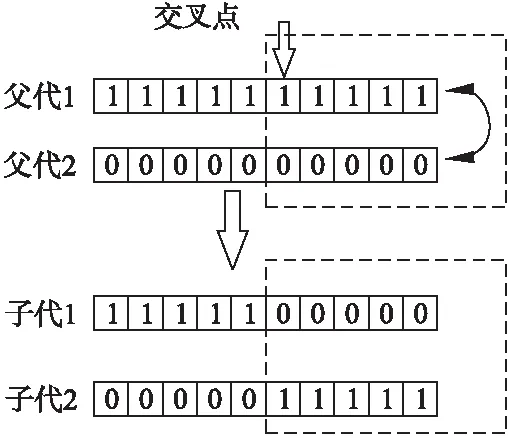
图2 交叉操作算子示意图Fig.2 Schematic diagram of crossover operator

3.2.4 变异算子

如图3所示,在交叉个体中,我们依概率选取个体执行变异操作.我们采取单点随机变异,在交叉个体中依照变异概率选取个体进行变异操作,随机选取基因位置进行反向变异.

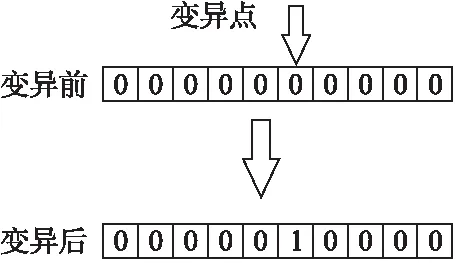
图3 变异操作算子示意图Fig.3 Schematic diagram of mutation operator

3.2.5 约束检测及修正算子

值得注意的是,在进化计算过程中,种群经过交叉和变异操作后会产生不满足卫星约束条件的个体,称为不可行解.我们提出约束检查及修正(Constraint Checking and Correction,CCC)算法,遍历种群中所有个体,进行约束检查,对不可行解进行约束修正,直至种群中所有个体均满足约束为止.算法主要步骤如图4所示.

图4 CCC算法主要步骤Fig.4 Main steps of the CCC

在算法CCC中,randomDelete函数执行随机删除输入集合中一个元素的操作;step 1-step 2从卫星观测任务集合中将需要执行的卫星观测任务选取出来;step 3-step 7检测单次开机时间约束,并将不满足约束的时间窗删除;step 8-step 15中,temp是不满足两次开机时间约束的连续窗口集合,所有不满足两次开机时间约束的窗口集合组成集合A;step 16- step 19对集合A中每一个集合调用randomDelete 函数,直到该集合满足两次开机时间约束为止,checkInterval函数只要输入集合中存在不满足两次开机约束的窗口,就返回ture;step 20将每一圈的时间窗选取出来分别组成集合;step 21-step 24对每一个集合调用randomDelete 函数,直到该集合满足单圈最长开机时间约束为止;step 25将每一天的时间窗选取出来分别组成集合;step 26-step 29对每一个集合调用randomDelete 函数,直到该集合满足单天最大开机次数约束为止.

3.2.6 更新算子

更新参考点z*,z*=(min(fDT(X)),min(fRC(X)));更新子问题的最优解xi,若f(xi)>f(yi),xi=yi;更新外部种群(EP).

4 实验及分析

目前卫星规划调度领域尚没有公认的Benchmark 测试问题集,为了验证我们提出算法的适用性和可行性,在AGI公司发布的星历数据库中选择了12颗卫星,在地图上选择16个点目标,模拟真实的多星任务规划过程,选择不同数量的点目标生成了不同规模、不同目标时间分辨率的测试数据集.我们选择了3种目标分辨率,分别为1小时(1h)、2小时(2h)、4小时(4h),具体测试数据集见表1.经过试验,得到了每个实验用例的进化情况和Pareto前沿.

设置卫星任务规划时段为24小时,计算平台为Core-i5 2.70 GHz,8G RAM,采用MATLAB编码.在算法中,我们取子问题规模和种群规模N=101,交叉概率为0.8,变异概率为0.15,进化代数为1000代.

表1 测试数据集Table 1 Testing dataset

每个用例得到的Pareto前沿如图5所示.

如图5可知,在SPCOSM计算过程中,种群的非支配前沿随着进化过程的推进逐渐散开,向Pareto最优解集逼近.SPCOSM算法的计算结果能够为操作员提供多目标决策数据支持,而不仅仅找到一个优化解.

为了验证我们提出算法的有效性,我们引入了求解该问题的一种基于启发式规则的搜索算法(Search Algorithm Based on Heuristic Rules for Satellite Periodic Continuous Observing Scheduling Problem,SABHR).

SABHR采用贪婪思想,其核心思路是:按照任务按照优先级从高到低的顺序依次处理,均以目标要求的时间分辨率截止点为起点,先按照时间顺序反向向前搜索,使用搜索到的第一个可用的访问时间窗口,若反向搜索没有找到可用访问时间窗口,再按照时间顺序正向向后搜索,安排搜索到的第一个可用的访问时间窗口,直到找到可用的访问时间窗口或遍历完所有时间窗口为止,从而得到一个可行的卫星观测方案.采用这样的策略,能够保证在尽量满足目标时间分辨率的前提下,降低卫星资源消耗.算法主要步骤如图6所示.

step1将任务按照优先级由高到低的顺序排序,step 2-step 8选出属于当前任务的访问时间窗,step 9将筛选的时间窗按照开始时间排序,step 10定义一个时间标签变量,记录使用窗口的结束时间,step 11-step 19将当前安排时间窗之后的时间窗分为两个集合,集合A表示未超过时间分辨率的时间窗,集合B表示超过的时间窗,step 20定义一个标签变量,表示是否找到一个未超出时间分辨率的时间窗,step 21-step 27选择集合A中按照时间顺序最后一个可用的时间窗,如果没有,则step 28-step 36选择集合B中按照时间顺序第一个可用的时间窗.安排时间窗时,均调用SetConflictFlag函数将与当前安排时间窗不满足公式(1)-公式(4)约束的时间窗冲突标志置为yi=1,如step 24和step 32.

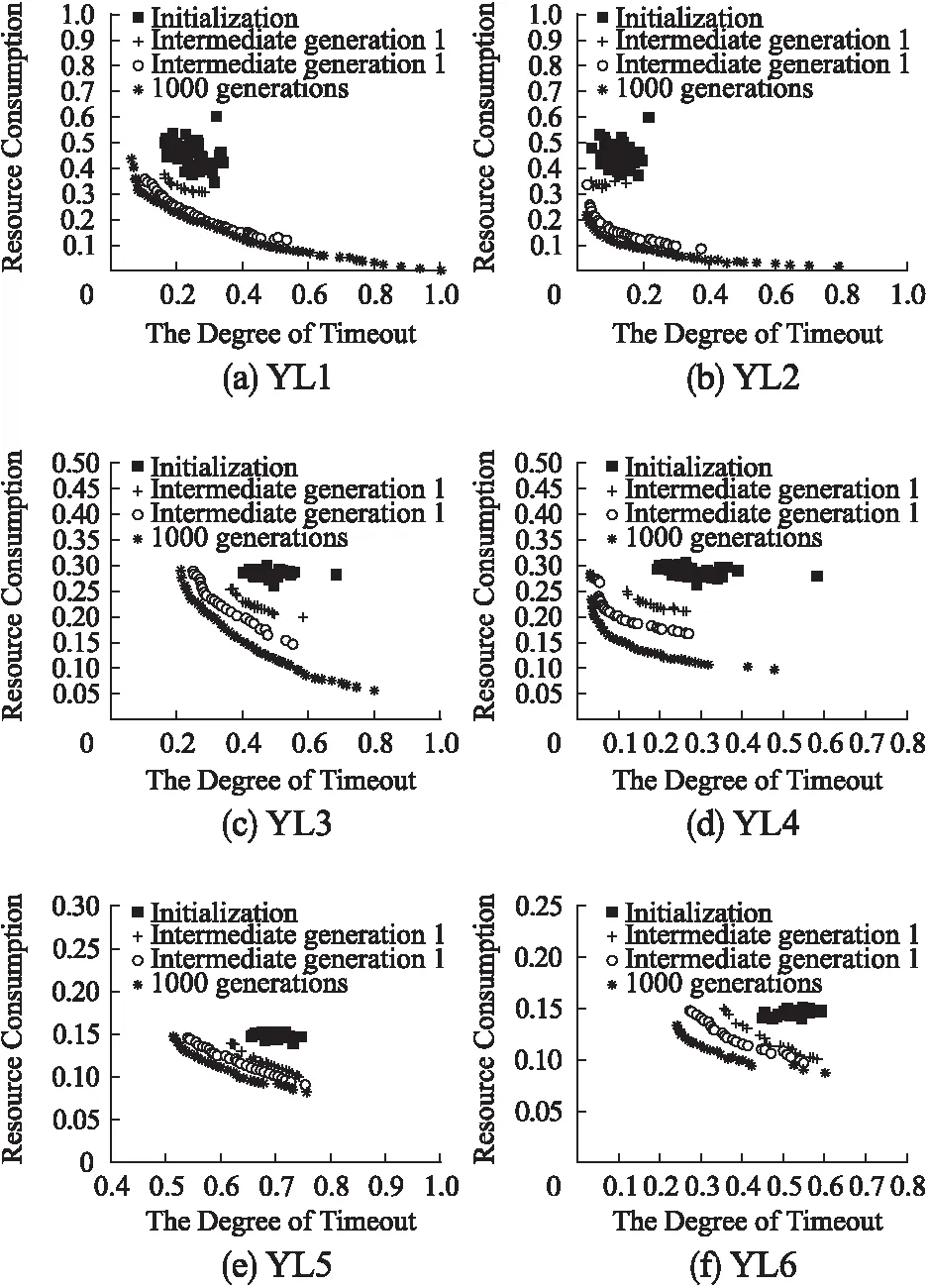
图5 目标空间和Pareto前沿Fig.5 Objective space and Pareto front

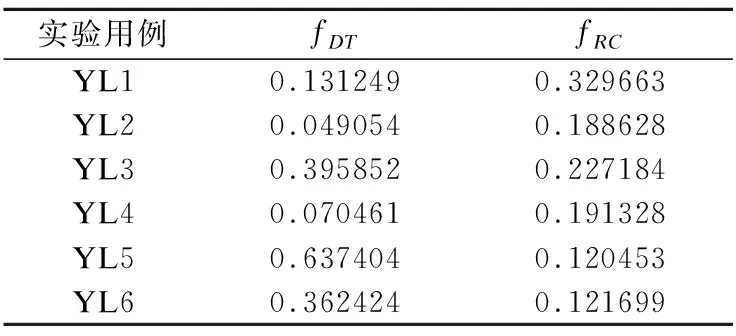
表2 SABHR算法的结果Table 2 Results of SABHR algorithm

在测试数据集上,使用SABHR算法,得到了卫星可用的观测方案,通过(7)式和(8)式计算出方案总超时程度和资源消耗,如表2所示.

将SABHR算法的解和SPCOSM算法的Pareto解集分别在方案总超时程度、资源消耗和综合两个优化目标三个方面做了比较比较,将SPCOSM的Pareto解集中支配SABHR的解的个数分别做了统计,如图7-图9所示.

图6 SABHR的主要步骤Fig.6 Main steps of the SABHR

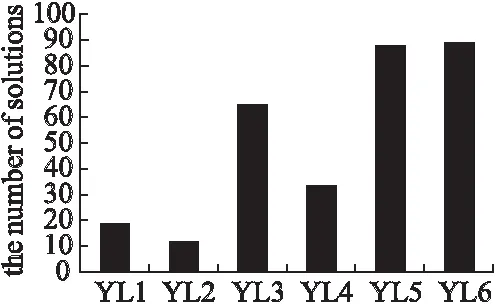
图7 在DT上SPCOSM支配SABHR解的数量Fig.7 Number of solutions that SPCOSM dominates ABHR on DT

从图7、图8和图9中,可以看出SPCOSM算法能够得到比SABHR算法质量更好的解,且能够提供大量的方案供操作员选择,这表明SPCOSM算法具有有效性和实用性.

5 结论及下一步工作

本文针对卫星周期性持续观测任务规划问题,建立了约束满足问题模型,采用基于分解的多目标优化框架,提出了基于分解的卫星观测调度多目标算法(SPCOSM),并设计了仿真实验.结果表明,算法能够求得较好质量的Pareto前沿.能够有效求解组网卫星周期性持续观测任务规划问题.

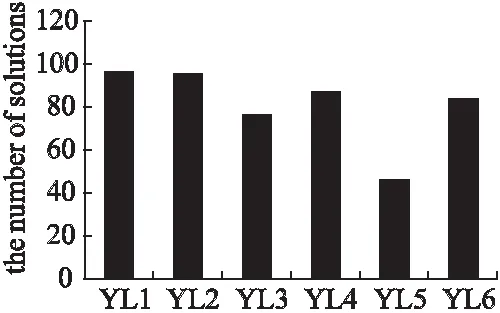
图8 在RC上SPCOSM支配SABHR解的数量Fig.8 Number of solutions that SPCOSM dominates SABHR on RC

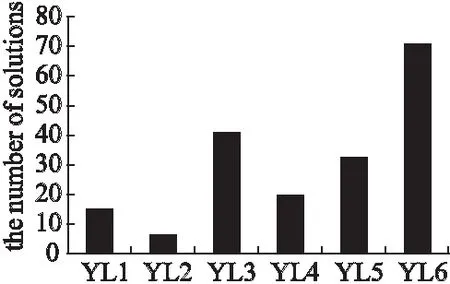
图9 SPCOSM支配SABHR解的数量Fig.9 Number of solutions that SPCOSM dominates SABHR

SPCOSM算法会计算整个Pareto前沿,但操作员通常只关注某一特定解空间内的Pareto优化解集,而非整个Pareto前沿.这就是用户的偏好信息.所以,我们下一步的工作在于将研究基于偏好的多目标优化方法在卫星任务规划中的应用.

：

[1] Lin Zhen-hai.Mission planning for electromagnetic environment monitors satellite based on simulated annealing algorithm[C].Proceeding of IEEE Canadian Conference on Electrical and Computer Engineering (CCECE),2015:530-535.

[2] Steve Chien,Joshua Doubleday,David Mclaren,et al.Monitoring flooding in thailand using earth observing one in a sensorweb[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2013,6(2):291-297.

[3] Lin Wei-cheng,Liao Da-yin,Liu Chung-yang,et al.Daily imaging scheduling of an earth observation satellite[J].IEEE Transactions on Systems,Man,and Cybernetics-Part A:Systems and Humans,2005,35(2):213-223.

[4] Li Yu-qing,Wang Ri-xin,Liu Yu,et al.Satellite range scheduling with the priority constraint:an improved genetic algorithm using a station ID encoding method[J].Chinese Journal of Aeronautics,2015,28(3):789-803.

[5] Chen Ying-wu,Yao Feng,Li Ju-fang,et al.A learnable ant colony optimization to the mission planning of multiple satellites[J].Systems Engineering-Theory & Practice,2013,33(3):791-801.

[6] Jiang Wei,Pang Xiu-li,Hao Hui-cheng.Collaborative scheduling model and algorithm for imaging satellite network[J].System Engineering and Electronics,2013,35(10):2093-2101.

[7] Wang Jian-jiang,Zhu Xiao-min,Yang Laurence T,et al.Towards dynamic real-time scheduling for multiple earth observation satellites[J].Journal of Computer and System Sciences,2015,81(1):110-124.

[8] Chen Hao,Wu Jiang-jiang,Shi Wen-yuan,et al.Coordinate scheduling approach for EDS observation tasks and data transmission jobs[J].Journal of Systems Engineering and Electronics,2016,27(4):822-835.

[9] Wang Chen,Chen Hao,Zhai Bao-rong,et al.Satellite observing mission scheduling method based on case-based learning and a genetic algorithm[C].Proceedings of IEEE International Conference on Tools with Artificial Intelligence (ICTAI),2016:627-634.

[10] Chen Yu,Zhang Deng-yi,Zhou Meng-qiang,et al.Multi-satellite observation scheduling algorithm based on hybrid genetic particle swarm optimization[M].Advances in Information Technology and Industry Applications,Springer Berlin Heidelberg,2012:441-448.

[11] Zhang Qing-fu,Li Hui.MOEA/D:a multi-objective evolutionary algorithm based on decomposition[J].IEEE Transactions on Evolutionary Computation,2007,11(6):712-731.

[12] Yu Wei,Li Bai-zhan,Jia Hong-yuan,et al.Application of multi-objective genetic algorithm to optimize energy efficiency and thermal comfort in building design[J].Energy and Buildings,2015,88:135-143.

[13] Li Hui,Zhang Qing-fu.Multi-objective optimization problems with complicated Pareto sets,MOEA/D and NSGA-II[J].IEEE Transactions on Evolutionary Computation,2009,13(2):284-302.

[14] Wang Zhao,Gong Mao-guo,Lei Yu,et al.A memetic algorithm based on MOEA/D for near space communication system deployment optimization on tide user model[C].Proceeding of IEEE Congress on Evolutionary Computation (CEC),2016:3614-3621.

[15] Zhao Fu-qing,Chen Zhen,Wang Jun-biao,et al.An improved MOEA/D for multi-objective job shop scheduling problem[J].International Journal of Computer Integrated Manufacturing,2016,30(6):616-640.

[16] Ding Da-wei,Wang Gang.Modified multi-objective evolutionary algorithm based on decomposition for antenna design[J].IEEE Transactions on Antennas and Propagation,2013,61(10):5301-5307.

附中文参考文献：

[5] 陈英武,姚 锋,李菊芳,等.求解多星任务规划问题的演化学习型蚁群算法[J].系统工程理论与实践,2013,33(3):791-801.

[6] 姜 维,庞秀丽,郝会成.成像卫星协同任务规划模型与算法[J].系统工程与电子技术,2013,35(10):2093-2101.