感应测速磁体极性布置对测速精度影响

张明宏，孙 浩

(1.安徽东风机电科技股份有限公司， 合肥 231202； 2.南京理工大学 机械工程学院， 南京 210094)

随着国际形势的发展和反恐的需要，对单兵火箭弹的需求越来越大，当单兵火箭弹采用杀爆战斗部时，为提高弹药对敌方人员的杀伤威力，常采用时间引信[1-2]。由射手测得发射管距目标间距离，装订于引信上，引信根据事先输入的弹丸“标准速度”解算出作用时间[3]。在不对弹丸测速情况下，由于每发弹丸的实际速度与“标准速度”存在差异，造成炸点散布大，战斗部杀伤半径有限，很难对敌方设施有效打击。现对每发弹药进行测速，然后通过有线装定或感应装定将此数据装定于引信电路上，这样弹丸炸点精度提高。

弹丸测速方法有多种，本研究采用的是发射管上安装磁体，弹丸上缠绕线圈的方法。根据电磁感应原理，不同的磁体极性布置在感应测速时，将在线圈中产生不同的电动势波形，并不是所有的波形都适合作为测速信号[4-5]。本研究通过对不同的磁体极性布置产生的波形进行仿真，为设计者提供指导。

1 感应测速模型的建立

单兵火箭弹从发射管发射出去是一个动态的过程，现建立三维瞬态场的有限元模型。该瞬态过程包括电磁过程和机械过程两部分。在处理机械瞬态过程中，需要引入对位移和角度的离散计算，其离散格式可以按照式(1)描述。

(1)

其中：x是机械位移量，可以是位移也可以是角度。此外，对于非线性的处理可以采用Newton-Raphson算法。

将T-算法应用于三维瞬态场的模型计算，由三维瞬态运动所产生的效应可以通过局部剖分法计算，低频瞬态磁场时，将麦克斯韦方程组写为式(2)

(2)

基于式(2)，构造出两个恒等式

(3)

在求解三维瞬态磁场时，其棱边上的矢量位自由度采用一阶元计算，而节点上的标量位自由度采用二阶元计算。

仿真过程主要包括：三维实体建模、材料和激励给定、剖分和求解设定、瞬态计算结果分析[6,7]。三维实体模型如图1所示。

该三维模型的相关参数如下：感应线圈内部半径40 mm,外部半径42 mm，匝数为50匝，采用绞线型绕组，材料铜copper，模型为正多边形环，激励源为外部激励。弹丸对脉冲信号的波形影响较小，为了简化计算过程，忽略弹丸对脉冲信号的波形影响。弧形磁块厚度2 mm,宽度5 mm,圆心角为60°，两两对称于Z轴，内嵌于身管中，磁铁的材料采用钕铁硼，矫顽力Hc为-907 000 A/m,剩磁强度Br为500 G。指定运动域Band和求解域region，材料均设置为真空vacuum。Band为实体正多边形圆柱，用于分隔运动物体和静止物体和限制运动范围，region为实心圆柱，包裹所有模型。模型的运动设置：感应线圈随弹丸沿Z轴正向运动，速度V=170 m/s，运动范围为0～170 mm,运动时间1 ms,运动步长为0.01 ms。以上参数为固定参数。

2 仿真结果

仿真时设置两组磁块轴向间距为55 mm,磁体和感应线圈的径向间距为3 mm。根据磁铁极性布置分两种情况，一是沿发射管轴线方向充磁，二是沿发射管径向方向充磁。

2.1 沿轴线方向充磁时产生的信号波形

沿发射管轴线方向充磁时存在4种情况，为了便于区分描述，现将沿Z轴负方向充磁时磁块的极性布置表示为NS-NS，其磁力线分布如图2所示。4种情况可以分别用NS-NS、SN-SN、NS-SN、SN-NS描述，4种布置方式如图3所示，经仿真得到4种布置方式测速波形图，如图4所示，其中图4(a)与图4(c)波形反向，图4(b)和图4(d)波形反向。

2.2 沿发射管径向充磁时产生的信号波形

沿发射管径向方向充磁时，存在3种情况：磁铁中两个磁块均沿径向向内充磁、沿径向向外充磁、向相同的方向充磁。3种布置方式如图5所示，对3种情况经仿真分析，得到波形图如图6所示。

3 磁铁极性布置对测速精度的影响分析

3.1 沿轴线方向充磁时产生的信号波形对测速精度的影响

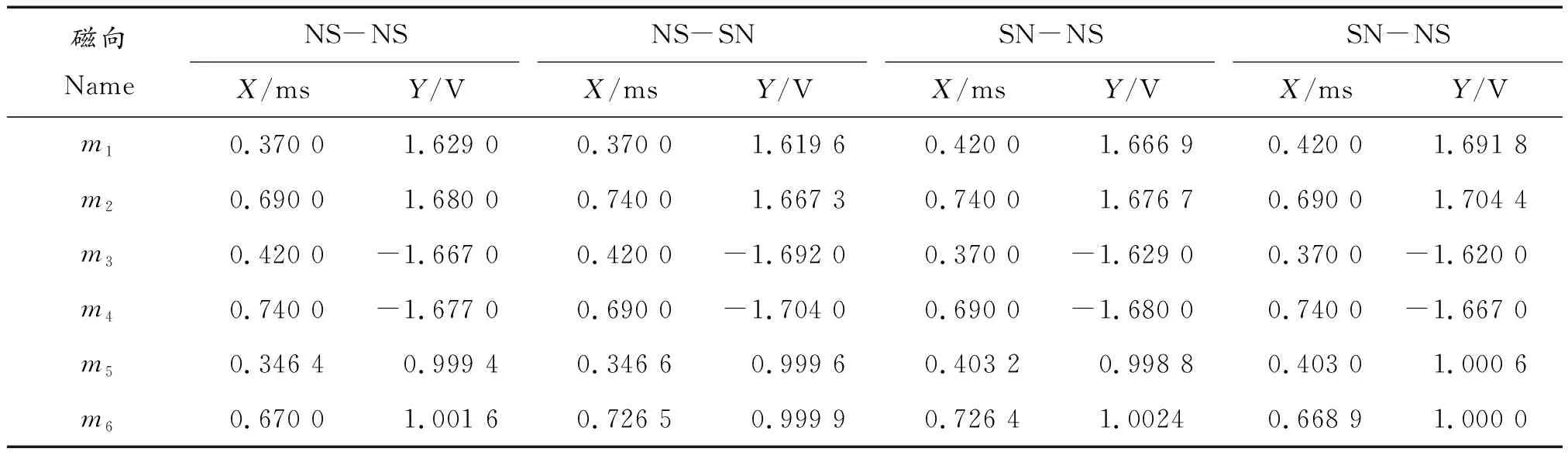
表1为图4波形图中选取点的坐标，X轴是时间，Y轴是线圈中感应电动势信号，m1、m2、m3、m4点均为波峰、波谷顶点，m5、m6点为选取各波形上升段3/4处点，各点数值如表1所示。

1) 由图4(a)和图4(c)可以看出，当两组磁铁具有相同的极性方向时，即以NS-NS和SN-SN布置，感应线圈产生的信号波形为近似的正弦波，两组脉冲信号波形一致，具有较好的重复性，且具有陡峭的上升沿与下降沿。

磁向NameNS-NSX/msY/VNS-SNX/msY/VSN-NSX/msY/VSN-NSX/msY/Vm10.370 01.629 00.370 01.619 60.420 01.666 90.420 01.691 8m20.690 01.680 00.740 01.667 30.740 01.676 70.690 01.704 4m30.420 0-1.667 00.420 0-1.692 00.370 0-1.629 00.370 0-1.620 0m40.740 0-1.677 00.690 0-1.704 00.690 0-1.680 00.740 0-1.667 0m50.346 40.999 40.346 60.999 60.403 20.998 80.403 01.000 6m60.670 01.001 60.726 50.999 90.726 41.00240.668 91.000 0

2) 由表1中数值可知，当采用NS-NS和SN-SN两种极性布置时，两波峰(谷)之间时间差为0.32 ms,又弧形磁块间距为55 mm，得到弹丸速度是171.88 m/s(磁块间距小，使用平均速度代替弹丸速度，误差可省略)，误差为1.1%。如将波峰(谷)临界点作为测速计时起始点，测量误差较大。在实际测速过程中，可选取波峰与波谷之间某一电压伏值作为触发电平。当选取波形上升段3/4处点电压伏值作为触发电平时，NS-NS和SN-SN两种极性布置其计时时间差分别为0.3236 ms和0.3232 ms,计算出的弹丸速度为169.96 m/s和170.17 m/s,误差均小于为0.1%，具有相当高的测速精度。故此两种极性布置方式适合在引信测速机构中应用，而且在计时起始点选取上选波形上升段3/4处点优于选波峰(谷)点，两者之间时间间隔误差更小，测速精度更高。

3) 同样由表1中数值可知，当采用NS-SN极性布置时，波峰和波谷的时间间隔分别为0.27 ms和0.37 ms,计算出速度为203.70 m/s和148.65 m/s，若选取波形上升段3/4处点电压伏值作为触发电平时，测得的速度为206.84 m/s,3组数据相差很大，同弹丸真实速度有很大误差，不适合应用在引信测速机构中。NS-SN布置时的分析同SN-NS，也不适合在引信测速机构中应用。

3.2 沿发射管径向充磁时产生的信号波形对测速精度的影响

表2为图6波形图中选取点的坐标，X轴是时间，Y轴是线圈中感应电动势信号。m1、m2点均为波峰、波谷顶点，m3、m4点为选取各波形上升段或下降段3/4处点，各点数值如表2所示。

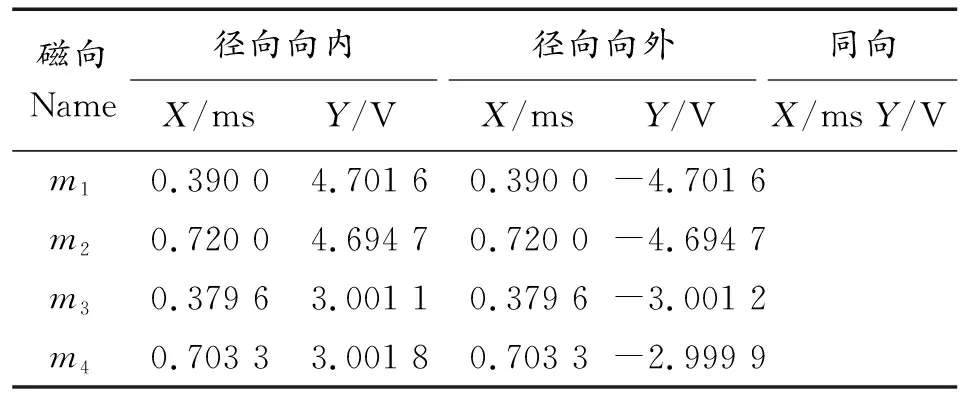
表2 磁块极性沿径向布置时选取点

1)由图6(a)和图6(b)可以看出，沿径向向内和沿径向向外两种磁块极性布置产生的的信号波形是关于时间轴X对称的，两种情况的波形都具备陡峭的上升沿和下降沿，有利于选取计时信号，计时开始脉冲和计时终止脉冲的一致性良好。

2) 由表2数值可知，当采用径向向内和径向向外两种极性布置时，两波峰(谷)的时间差为0.33 ms,可得速度v=166.67 m/s,，误差为1.95%，如将波峰(谷)临界点作为测速计时起始点，测量误差较大。同样当选取波形上升段3/4处点电压伏值作为触发电平时，计算可得其两种情况时间差均为0.323 7 ms，计算得出所测速度为169.91 m/s，误差均小于0.1%，具有相当高的测速精度。故此两种极性布置方式适合在引信测速机构中应用。

3) 当沿径向相同的方向充磁时，感应电动势信号为一串微弱的不稳定谐波，无法进行及时测速，故该磁铁极性布置方案不适合在引信测速机构中应用。

4 验证

尽管相距为L的两组磁体布置在发射管口部，但测得的速度还不是弹丸的最大初速，弹丸在膛內还有一段加速过程，因此还需要对测得的速度根据内弹道理论进行推算，解算出弹丸最大初速V0。弹丸射击时，引信微处理器根据事先装订的目标距离S，以及由通过电磁感应测得的弹丸速度V推算出的弹丸最大初速V0，由弹道解算出引信作用时间t。

检验弹丸感应测速准确性试验现场图如图7所示，通过读取回收引信测速电路存储的测速数据V，与发射管口通过高速摄像测得的弹丸速度V0相比较，观测V与V0数值大小一致性。

某口径单兵火箭弹初速170 m/s，在同一温度下初速散布±3 m/s，在高温(+50 ℃)与低温(-40 ℃)情况下初速又有很大差异，在不采取测速情况下(引信只装订作用距离，不装订速度)该单兵火箭弹在380 m处引信空炸精度是±12 m。通过测速(引信既装订作用距离，又装订速度)，当采用沿轴线NS-NS方向进行磁体极性布置时，可将该火箭弹在380 m处引信空炸精度提高到±5 m(纵向)，证明了此方法的可行性。

5 结论

利用Ansoft Maxwell软件对不同的磁体极性布置仿真，得出不同的感应测速波形，并对不同的感应波形对测速精度的影响进行了分析，有的波形适合测速，有的波形不适合测速，甚至无法测速，为设计者指出了有效的几种感应测速磁体极性布置方式，同时也指出了在测速波形上计时起始点选取对测速精度也有不同程度的影响。实验结果表明，当采用沿轴线NS-NS方向进行磁体极性布置时，通过测速可将某口径单兵火箭弹在380 m处引信空炸精度由原来不经测速的±12 m提高到±5 m(纵向)，该口径火箭弹有效杀伤半径7 m，通过测速提高了该火箭弹作战效能。同样对其他弹药感应测速系统的设计具有一定的指导意义。

[1] 洪黎，张合，李豪杰，等.单兵火箭弹自主式初速存储测试系统研究[J].测试技术学报，2013(1)：8-13.

[2] 洪黎，张合，李豪杰，等.单兵火箭弹作用时间自适应修正方法[J].仪器仪表报，2013(8)：1916-1920.

[3] 翟性泉，陈荷娟.电子时间引信作用时间的自修正方法[J].弹道学报，2013(3)：44-47.

[4] 姚家红，才伟，张明宏.平衡抛射式火箭弹筒口测速技术研究[J].价值工程，2016(5)：193-194.

[5] 范建英.弹丸炮口速度测试技术研究[D].太原:中北大学，2014.

[6] 赵博，张洪亮.Ansoft12 在工程电磁场中的应用[M].北京：中国水利水电出版社，2010.

[7] SHELDON L，CYTRON.Apparatus and method for measuring exit velocity of a gun round[P].US.Pat:6644111B1,2002-05-21.