下保护罩对PMT水下内爆载荷特性传播影响的数值研究

王天穹，方志威,2，侯海量，金 键，吴林杰，李 茂

(1.海军工程大学 舰船与海洋学院，武汉 430033； 2.中国人民解放军91189部队， 江苏 连云港 222041)

中微子作为构成物质世界的最基本单元之一，具有独特的性质。对中微子问题的研究有助于完善对物质世界最基本规律的认识，但是中微子作为一种穿透性非常强的粒子极难探测，世界上许多国家计划或者已经开展了中微子探测试验[1-2]。光电倍增管(Photo Mutiplier Tube简称PMT)是用于探测中微子的核心部件，可以提供物理分析的实验数据。但PMT是由透明玻璃吹制而成，内部接近真空，工作状态下承受静水压力。玻璃蠕变、疲劳损伤、生物侵蚀、初始缺陷等多种原因都会导致PMT意外破坏。当PMT在静水压力下发生内爆后，产生的冲击波在向四周传播的过程中有可能击破相邻的PMT，导致水中所有PMT发生连锁内爆。日本超级神冈中微子探测器PMT发生内爆后，冲击波导致临近700多个PMT发生殉爆；这次爆炸不仅造成严重的经济损失，还导致试验延误4年[3]。事故发生后世界上大型水下中微子探测工程开始重视水下PMT的防爆性能[4-11]。

本文以广东大亚湾的江门中微子实验中心的PMT为研究对象，通过数值计算方法研究PMT内爆后的载荷特性，考虑到PMT在静水压力下发生爆炸后产生的冲击波有可能击破相邻的PMT，提出了在PMT中增加下保护罩，探讨了下保护罩对PMT内爆载荷特性的影响。

1 数值计算模型

江门中微子实验中心的探测器安装于直径43 m、深45 m的圆柱型水池中(如图1所示)；中心探测器外层与水池之间注满超纯水，水密度为1 000 kg/m3；20 000只PMT密布在图1所示的不锈钢网架和水池内壁上，水池内的PMT承受0.1～0.54 MPa的静水压力。

1.1 PMT及下保护罩尺寸

PMT示意图及外形尺寸图如图2。PMT由玻璃外壳(简称玻壳)与内部电气原件组成，其中玻壳厚度约为4～6 mm，PMT内部电气结构为金属材料，工作在真空之中，内部真空度为10-5Pa以上。下保护罩壁厚为3 mm，材料为不锈钢，下保护罩开有3个直径为40 mm的孔，这是方便PMT内爆后水流入下保护罩内，下保护罩示意图及尺寸图如图3。

1.2 有限元模型

利用通用有限元软件Patran建立计算模型，如图4和图5。建模过程中采用kg-mm-ms单位制。考虑计算模型是轴对称的，为减少计算量和提高计算效率，建立1/4模型。数值计算模型中XOZ和YOZ平面为对称面，设置对称边界条件，XOY平面为池底，设置为刚性壁；除发生内爆的PMT(A区域所示)外，其余PMT表面均设置为刚性壁。

有限元模型中A区域为真空区域，真空度为10-5Pa；其余区域为水域，密度为1 000 kg/m3；图5中B区域为下保护罩，最外层区域(为一层有限元单元)为环境单元。由于江门中微子试验中心水池深度为45 m，因此只选取最危险工况即45 m水深处PMT的工作环境设置常压，常压值为0.545 MPa。

有限元模型中采用稀薄空气代替PMT内部真空度。假设稀薄空气为理想气体，状态方程为：

P=(γ-1)ρe

(1)

式中，P为空气压力，设为10-5Pa；ρ为空气密度；e为内能，可取为1.972 7×105J/kg；γ为比热，可取为1.4，通过式(1)可知要使PMT内部真空度达到10-5Pa，对应的内部稀薄空气密度应为1.28×10-10kg/m3。

水域的状态方程采用Mie-Gruneisen方程：

式中:P为水的压力；μ为水的压缩度；V0为水的相对初始体积；ρ为水的密度，可取为1 000 kg/m3；c为vs-vp曲线的斜率(声速)，可取1 484 m/s；γ0为Gruneisen参数，可取为0.11；a为γ0和μ的一阶体积修正量，可取3；S1、S2、S3分别为曲线拟合参数，取S1=1.979、S2=S3=0。E为水的初始体积内能，由于水几乎不可压缩，因此可以设为0。选取水池最深45 m处为初始水压，即0.54 MPa。通过求解状态方程可以得到V0=0.999 754 6。

下保护罩厚度为3 mm；采用Elastic材料模型描述，密度为7.9×10-3kg/m3；弹性模型为200 GPa；泊松比为0.3。

为了更好的分析计算模型中PMT爆炸产生的冲击波强度及其传播规律，在PMT的Z+方向(测点A1-A4)、Z-方向(测点B1-B4)、Z+X+(测点C1-C4)方向、Z-X+(测点D1-D4)、X+方向(测点E1-E2)方向共布置了18个压力测量点，如图6所示。

2 PMT水下内爆数值计算结果分析

2.1 PMT水下内爆过程分析

PMT内爆有限元模型计算过程中C区域为真空域，密度为1.28×10-10kg/m3，其余区域为水域，密度为1 000 kg/m3；可以通过观测有限元模型中不同区域的密度变化来观测PMT的内爆过程。图7和图8分别为无下保护罩PMT和存在下保护罩PMT在计算过程中典型时刻密度分布云图。

由图可知在无下保护罩情况下，PMT发生内爆后，四周水域立刻向真空区域汇聚，如图7(a)和7(b)所示，大约在11 ms时，真空区域完全发生溃灭；真空区域完全溃灭后，在PMT底部圆柄处出现射流，如图7(d)所示；而存在下保护罩的PMT发生内爆后，水域从PMT顶部开始发生坍塌，向下汇聚，PMT下保护罩的存在阻碍了PMT底部水向PMT内部汇聚，如图8(a)和8(b)所示，大约在14 ms时，真空区域完全发生溃灭。下保护罩的存在延缓了真空区域完全溃灭的时间。

2.2 无下保护罩PMT水下内爆载荷特性

无下保护罩的PMT发生内爆后在Z+、Z-、Z+X+、Z-X+、X+方向测点的压力时程曲线分别如图9-图13所示，而无下保护罩的PMT发生内爆后Z+、Z-、Z+X+、Z-X+、X+方向压力测点载荷特性如表1所示。

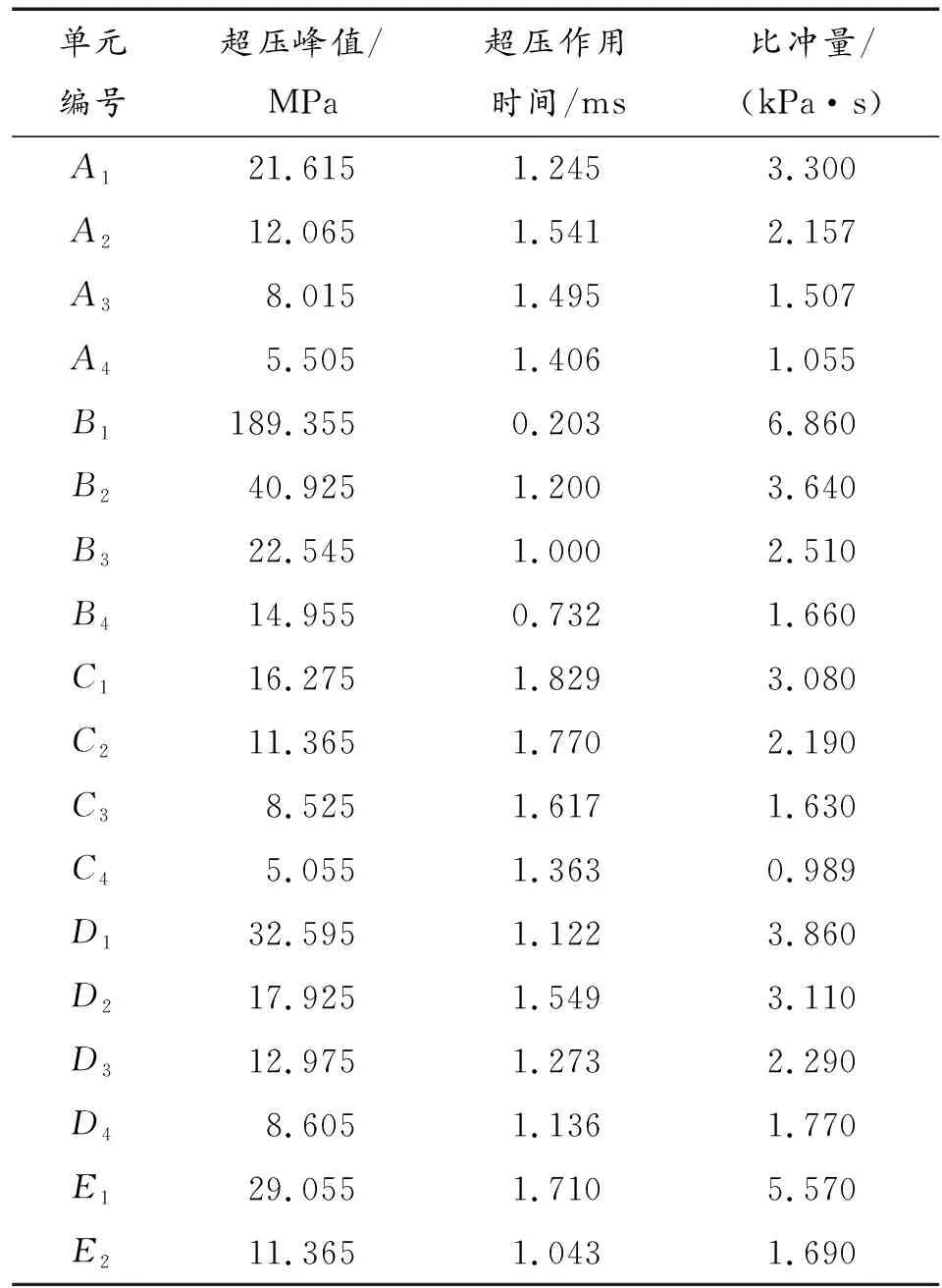
单元编号超压峰值/MPa超压作用时间/ms比冲量/(kPa·s)A121.6151.2453.300A212.0651.5412.157A38.0151.4951.507A45.5051.4061.055B1189.3550.2036.860B240.9251.2003.640B322.5451.0002.510B414.9550.7321.660C116.2751.8293.080C211.3651.7702.190C38.5251.6171.630C45.0551.3630.989D132.5951.1223.860D217.9251.5493.110D312.9751.2732.290D48.6051.1361.770E129.0551.7105.570E211.3651.0431.690

通过对图14和图15所示PMT发生内爆后在Z+、Z-、Z+X+、Z-X+、X+方向压力时程曲线与载荷特性分析，可知最大压力峰值和比冲量分别出现在A1、B1、C1、D1和E1压力测点，压力峰值出现时间区间为10.5～12.0 ms。进一步分析可得PMT水下内爆载荷特性规律如下：(1) PMT内爆后产生的冲击波在Z+方向、Z-方向、Z+X+方向、Z-X+方向、X+方向传播时，越是靠近PMT的几何中心O(即PMT椭圆形中心)处的压力测点，其压力峰值出现的时间点越早，压力峰值越大；越是远离PMT的几何中心O处的压力测点，其压力峰值出现的时间点越早，压力峰值越大。(2) PMT内爆后产生的冲击波向四周传播时，位于PMT内部的压力峰值衰减明显，而位于水域中的压力峰值衰减相对较小。(3) 通过对PMT内爆后Z+方向、Z-方向、Z+X+方向、Z-X+方向的压力峰值和比冲量进行拟合，可知Z-方向的压力峰值和比冲量最大，这是因为PMT内爆后在圆柄处产生射流造成的；PMT内爆后产生的冲击波向四周传播的过程中，向Z-方向传播的能量最大，即PMT由底部向外传播的冲击波最大。

通过对传播方向的压力峰值和比冲量进行拟合，由拟合曲线可知幂函数拟合曲线与测点的压力峰值与比冲量吻合均较好，拟合曲线整体趋势相同，可以得知PMT内爆后产生的压力峰值和比冲量在传播方向上均呈现幂函数形式衰减。

2.3 存在下保护罩PMT水下内爆载荷特性

存在下保护罩的PMT发生内爆后在Z+、Z-、Z+X+、Z-X+、X+方向测点的压力时程曲线分别如图16-图20所示，存在下保护罩的PMT发生内爆后Z+、Z-、Z+X+、Z-X+、X+方向压力测点载荷参数如表2所示。

进一步分析可得PMT水下内爆载荷特性规律如下：

1) 存在下保护罩的PMT内爆后产生的冲击波在Z+方向、Z+X+方向、Z-X+方向、X+方向传播时，越是靠近PMT的几何中心点O(即PMT椭圆形中心)处的压力测点，其压力峰值出现的时间点越早，压力峰值越大；越是远离PMT的几何中心O处的压力测点，其压力峰值出现的时间点越晚，压力峰值越小；而在Z-方向上，冲击波强度随着距离几何中心点O的距离增加而增大。由于下保护罩的存在，PMT内爆后水流从PMT顶部向下坍塌，在PMT底部灯座上部产生抨击，因此该处冲击波强度最大。

2) 存在下保护罩的PMT内爆后产生的冲击波向四周传播时，位于PMT内部的压力峰值衰减明显，而位于水域中的压力峰值衰减相对较小。

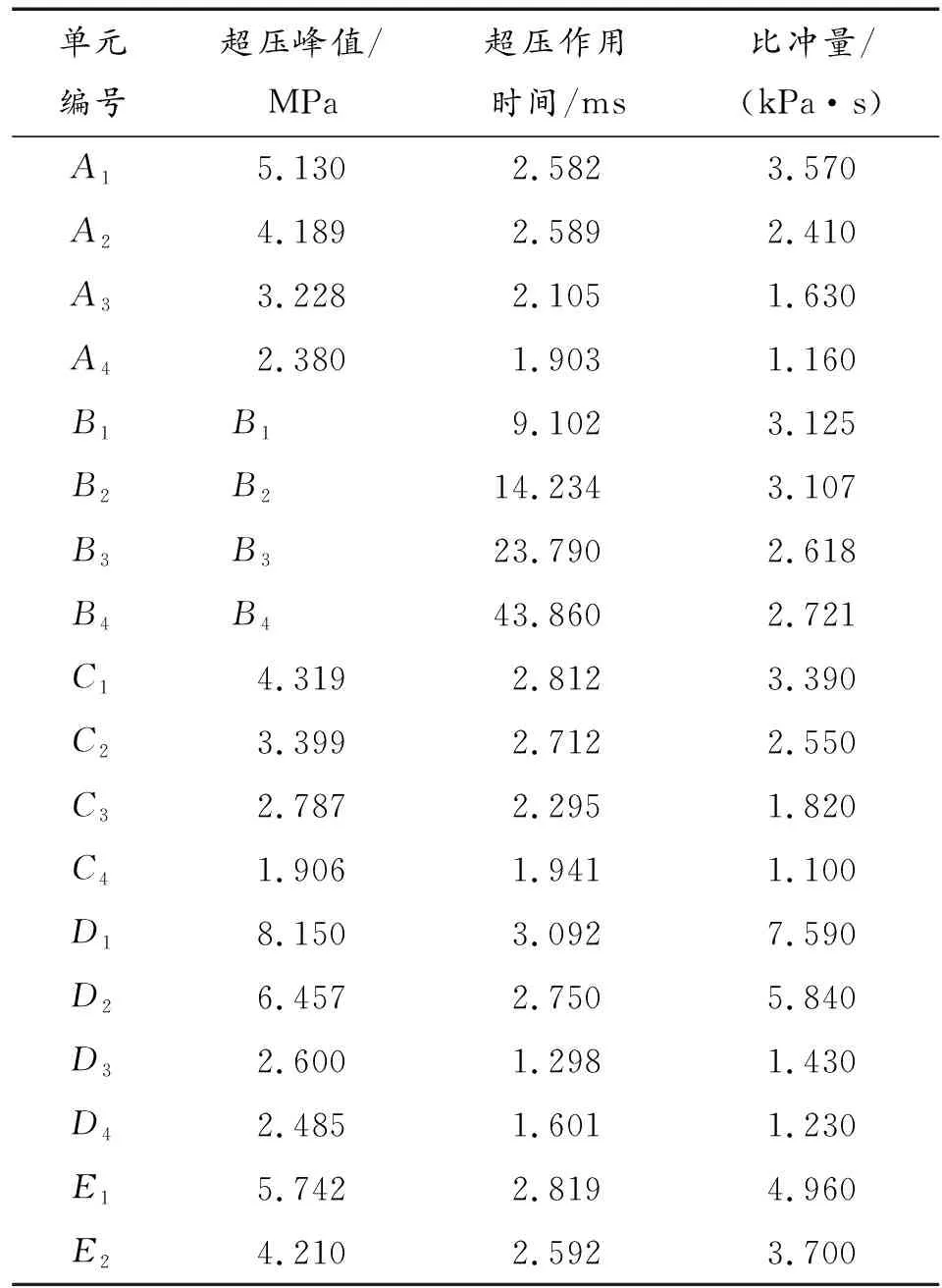
单元编号超压峰值/MPa超压作用时间/ms比冲量/(kPa·s)A15.1302.5823.570A24.1892.5892.410A33.2282.1051.630A42.3801.9031.160B1B19.1023.125B2B214.2343.107B3B323.7902.618B4B443.8602.721C14.3192.8123.390C23.3992.7122.550C32.7872.2951.820C41.9061.9411.100D18.1503.0927.590D26.4572.7505.840D32.6001.2981.430D42.4851.6011.230E15.7422.8194.960E24.2102.5923.700

通过对存在下保护罩的PMT内爆后各个方向的压力峰值和比冲量进行拟合，Z+方向、Z+X+方向、Z-X+方向传播时，幂函数拟合曲线与测点的压力峰值与比冲量吻合均较好，拟合曲线整齐趋势相同，可知在Z+方向、Z+X+方向、Z-X+方向传播时，压力峰值和比冲量在传播方向上均呈现出幂函数形式衰减；而在Z-方向传播时，指数函数拟合曲线与测点的压力峰值吻合均较好，压力峰值呈现指数函数形式增加，而在Z-方向比冲量呈现线性增加。

2.4 下保护罩对PMT水下内爆载荷传播特性影响

为了分析下保护罩对PMT内爆载荷传播特性的影响，制作了PMT内爆后冲击波强度与存在下保护罩PMT内爆后冲击波强度曲线对比，图23表示了对压力峰值的影响，图24表示了对比冲量的影响。

由图24可知，存在下保护罩的PMT内爆后的压力峰值普遍低于无下保护罩PMT内爆后的压力峰值，表明下保护罩能够很好降低压力峰值；下保护罩的存在还延迟了压力峰值出现的时间。冲击波在Z-方向传播时，存在保护罩的PMT的压力峰值在传播方向呈现指数函数形式增加，这是由于PMT内爆后水流从顶部向下坍塌撞击底座引起的，而没有下保护罩的PMT内爆冲击波在Z-方向传播时，压力峰值在传播方向呈现幂函数形式衰减。

由图24可知，存在下保护罩的PMT内爆后比冲量与不存在下保护罩的PMT内爆后的比冲量相当，这是因为虽然存在下保护罩的PMT压力峰值低于无下保护罩PMT的压力峰值，但存在下保护罩PMT超压作用时间较长，因此两者比冲量相当。

3 结论

以广东大亚湾的江门中微子实验中心的PMT为研究对象，通过数值计算方法研究了PMT内爆后的载荷特性，探讨了下保护罩对PMT内爆载荷特性的影响，主要得到以下结论：

1) PMT内爆产生的压力峰值和比冲量在传播方向上均呈现出幂函数形式衰减，PMT内爆冲击波向Z-方向传播的冲击波强度最大。

2) 存在下保护罩的PMT内爆产生的压力峰值和比冲量在Z+方向、Z+X+方向、Z-X+方向传播时均呈现幂函数形式衰减；而在Z-方向传播时，压力峰值呈现指数形式增加，比冲量呈现线性增加趋势。

3) 下保护罩的存在能够很好降低PMT内爆后产生的压力峰值，延迟压力峰值出现时间。存在下保护罩的PMT超压作用时间较长，其比冲量与无下保护罩的PMT相当。

[1] LING J J，BISHAI M，DIWAN M，et al.Implosion chain reaction mitigation in underwater assemblies of photomultiplier tubes[J].Nuclear Instruments and Methods in Physics Research A,2013,729：491-499.

[2] BRENNEN C E.Cavitation and bubble dynamics[M].Cambridge：Cambridge University Press，2013.

[3] FUKUDA S,FUKUDA Y,HAYAKAWA T,et al.The Super Kamiokande detector[J].Nuclear Instruments and Methods in Physics Research A,2003,501:418:-462.

[4] 王贻芳.大亚湾反应堆中微子实验[J].科学，2015，64(3)：5-8.

[5] 曹俊.大亚湾与江门中微子实验[J].中国科学：物理学 力学 天文学.2014，44：1025-1040.

[6] RAYLEIGH L.On the pressure developed in a liquid during the collapse of a spherical cavity[J].Philosophical Magazine Series 6，1917(34)：94-98.

[7] PLESSET M S.The dynamics of cavitation bubble[J].Journal of Applied Mechanics,1949(16)：813-821.

[8] IVANY R D,HAMMITT F G.Cavitation bubble collapse in viscous compressible liquids-numerical analysis[J].Journal of Applied Mechanics,1965(87)：977-985.

[9] HICKING R,PLESSET M S.Collapse and rebound of a spherical bubble in water[J].The physics of fluids,1964(7)：7-14.

[10] TURNER S E.Underwater implosion of glass spheres[J].The Journal of the Acoustical Society of Americal，2007，121(2)：844-852.

[11] COLE H R.Underwater explosion[M].Princeton，NEW Jersey：Princeton University Press，1948.