基于VMD算法的10 kV高压断路器机械故障诊断分析

田 书， 康智慧

(河南理工大学 电气工程与自动化学院，河南 焦作 454000)

0 引言

断路器是电力系统中重要的开断设备[1]，其可靠运行对整个输配电系统至关重要。在断路器各故障类型中，机械故障最为常见[2]，且机械特性可反映断路器80%以上的运行状态。振动分析法可通过压电传感器实时监测断路器机械故障信号，不涉及电气测量，可有效避免电磁干扰，是极具潜力的一种研究方法，逐渐成为断路器机械故障研究的热点[3-6]。

振动信号分析常采用的方法是经验模态分解[7]及集合经验模态分解[8]等。它们在非平稳、非线性信号处理方面表现出较好的时频聚集性。但是，在求取信号包络时采用的是极值点计算方式[9]，存在包络估计误差，通过多重递归分解，误差逐级放大，易出现过分解、端点效应及模态混叠现象，影响监测精度且不适合信噪比较低的场合。变分模态分解[10](Variational Mode Decomposition，VMD)由Konstantin Dragomiretskiy等人提出，是最新的一种信号处理方法。在获取IMF 分量时不同于传统的模态分解算法，它采用非递归分解方式，利用交替方向乘子法迭代求解各模态分量中心频率和带宽的最优解，自适应性强，在频域细分和各分量的有效分离中优势突出[11-12]，且具有较强的噪声鲁棒性，可以从复杂的工业环境中提取出关键特征信息。

VMD算法在2014年被提出之后，迅速被应用在机械领域及通信领域，文献[13]将VMD算法应用在轴承故障定子电流信号诊断中识别轴承主要故障特征，文献[14]利用VMD算法处理语音信号去噪问题，并取得良好效果。电力领域目前尚处于起步阶段，在高压断路器故障诊断方面的研究较少，因此本文提出将新算法应用在高压断路器并结合能量熵构造特征向量提取故障特征，拓宽断路器故障诊断研究领域。此外，为提高诊断精度，在信号分解时利用量子粒子群对VMD参数设置问题进行改进，使诊断结果更为精确。

1 改进VMD算法

变分模态分解的核心问题在于变分求解。当采用VMD算法对信号进行分解得到K个IMF时，其对应的变分模型如下：

(1)

式中：f(t)为输入信号；{uk}为IMF分量；{ωk}为各IMF的频率中心。在对上式求最优解时，需构造增广Lagrange函数，引入二次惩罚因子α与Lagrange乘子λ，增广拉格朗日表达式为：

(2)

此时，变分问题由一个约束性问题转变成非约束问题。

当采用VMD分解振动信号时，首先要对模态个数K和惩罚因子α的值进行设定，因为K决定了分解数量，α决定模态分量的带宽大小。实际信号复杂多变，为避免人为预设参数导致故障信息提取失真，本文利用量子粒子群算法[15]，以包络熵作为适应度函数，对VMD算法进行改进，实现参数寻优。具体改进步骤如下：

(1)设粒子位置为变分模态分解的参数[K,α]，初始化粒子群；

(2)在不同粒子位置下对信号进行变分模态分解，并计算每个粒子的适应度值，令包络熵最小值为局部极小值，根据各粒子的个体极值Pbest寻找全局极值gbest；

(3) 更新粒子的位置；

(4) 循环迭代，获取相应粒子的位置[K,α]。

为使参数优化更加精确，对信号参数进行10次寻优并取均值，最终优化结果为[K,α]=[5,979]，即模态分解层数为5，惩罚因子为979。

现场采集的振动信号往往伴随噪声的干扰，因此信号分解前需先进行降噪处理，本文采用小波阈值去噪，以db4小波作为基函数，对断路器振动信号进行降噪处理。去噪效果如图1所示。

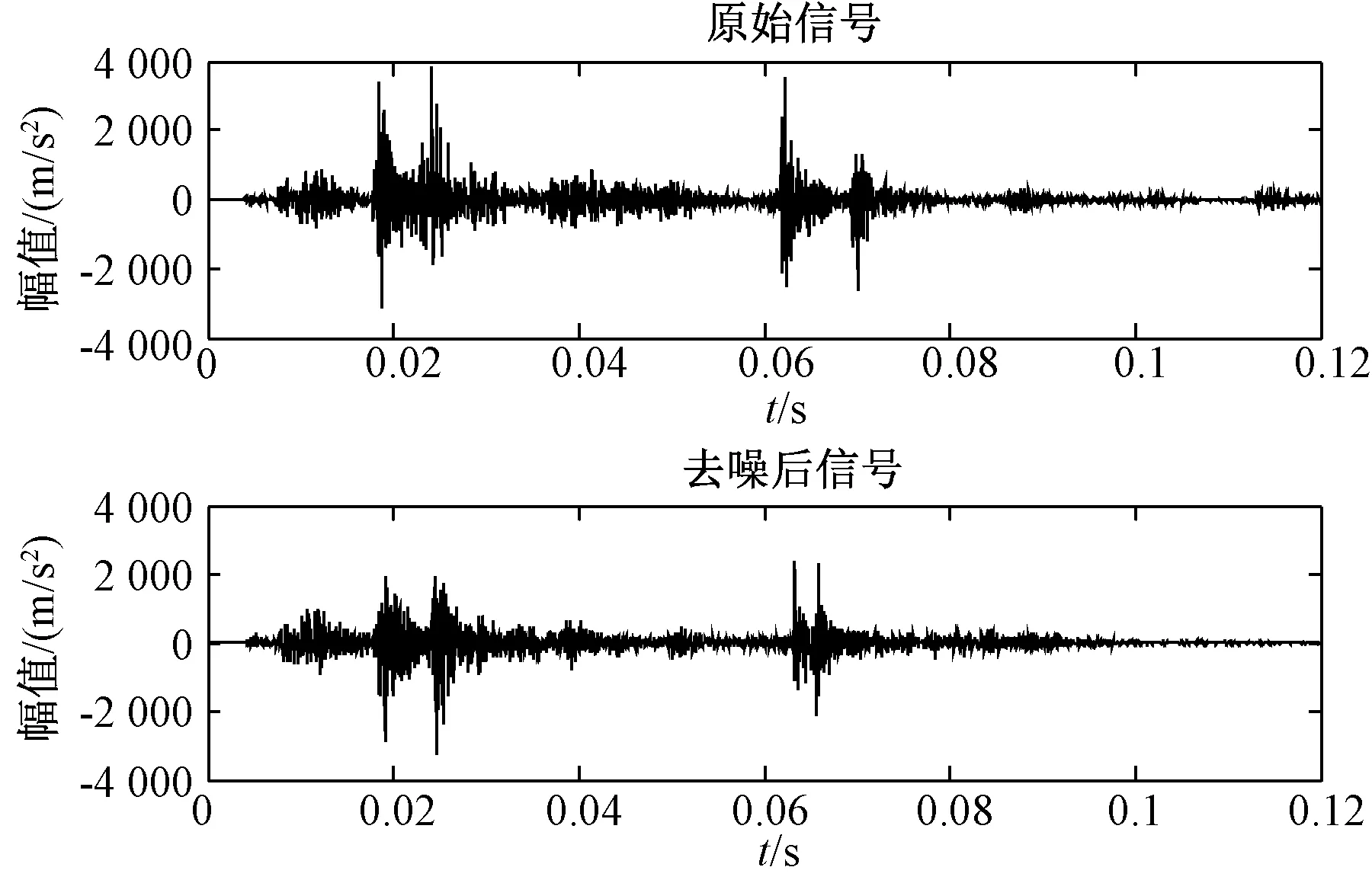
图1 振动信号去噪前后对比图

VMD作为一种新算法，为验证其在模态混叠及噪声鲁棒性方面的优势，本文将传统信号分析算法EEMD与VMD作对比。将去噪后的振动信号利用EEMD算法分解并求频谱图，结果见图2。采用VMD算法对信号进行分解并求频谱图，结果见图3。

图2 EEMD频谱

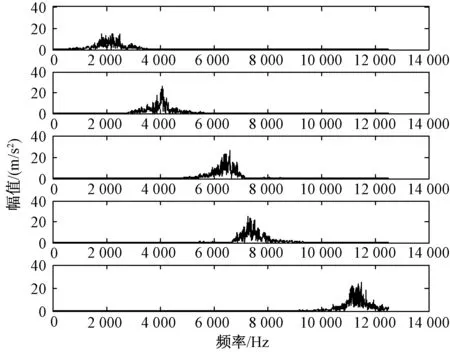
图3 VMD频谱

对比图2与图3可知，EEMD算法因本身存在包络估计误差及噪声幅值优化问题，导致模态混叠现象严重，每个IMF分量都包含多个频段信息。而VMD分解可将振动信号在频域上自适应剖分，使各分量有效分离，最终得到5个中心频段互不重叠的IMF分量，突出了信号的局部特征。

2 实验验证与分析

2.1 故障诊断步骤

首先对10 kV高压真空断路器ZN63 A-12设置实验室易实现的人为故障，构建数据样本。通过向断路器主传动轴外侧垫木块模拟传动机构卡涩故障，松动基座螺丝模拟断路器松动故障。故障信号采集测点通常选取在具有较高信号质量的关键部件振动源附近，目前，断路器故障诊断中常见的测点位置有灭弧室、断路器底座及两者之间的位置。考虑到断路器不同部位信号强度存在差异，基座松动状态时故障信号较弱，所以为保证微弱信号的有效采集，确保信号采集的完整度及准确度，结合ZN63A-12断路器自身的结构特点，经过反复试验，最终将测点选取在断路器底座附近。此处安装不会影响断路器正常工作，可避免磁性干扰，在保证测量准确有效的情况下，同时将安装工作量降至最低，具有很强的便捷性与实用性。传感器的固定方式有3种，分别为：磁铁吸附式、金属固持胶粘合式及螺栓固定式，其中磁铁吸附式操作简单，金属固持胶粘合式与螺栓固定式具有较高的信号保真度。在实验过程中，综合考虑3种传感器固定方式的优缺点，本文首先选用方式一寻找断路器的最优测点，然后在方式二与方式三之间选取最终的传感器安装方式。由于螺栓固定式需要对断路器钻孔，不仅破坏了断路器的结构，且增加了工作量，因此，在最优测点选取完成后，本文采用金属固持胶粘合式固定传感器，实现信号的采集工作。其中，传感器型号在压电式传感器YD系列、3700系列压阻式传感器之间选取，压阻式传感器具有较高的量程及频率响应范围，但其造价较高，考虑经济适用性，最终选用压电式传感器采集故障信号。由于断路器振动幅值主要分布在200～300 g，最高频段在10 kHz左右，本文所用传感器量程为500 g，频率响应范围为1～20 kHz，因此，满足实验要求。

断路器故障诊断具体过程如下：

(1) 传感器采集振动信号并进行变分模态分解。其中数据传输采集卡选用PCI8192，采样频率 25 kHz，振动数据采集时间为120 ms。

(2) 以改进VMD能量熵构造特征向量。

(3) 利用马氏距离(Mahalanobis distance)判别器诊断断路器故障状态。

故障诊断流程图见图4。

图4 故障诊断流程图

实验数据：

①36组正常振动信号(正常状态)。

② 30组传动机构卡涩振动信号(故障类型Ⅰ)。

参照上述的干法工艺流程图，按照正常处理1 t废旧电池干法处理模式，三元材料动力电池以传统的干法回收工艺计算成本和收益，LFP分别以传统的干法回收工艺（干法1）和改进的干法回收工艺（干法2）计算成本和收益，成本分别命名为CLFP干法1、CLFP干法2、C 三元干法，收益命名为 ELFP干法1、ELFP干法2、E 三元干法。处理成本价格根据实际调研及综合参考文献[6-7]，具体如表3所示。

③ 27组基座螺丝松动振动信号(故障类型Ⅱ)。

图5为3种工况的时域波形图。

图5 振动信号波形图

2.2 特征提取

特征提取是系统诊断故障的关键，能量熵在状态定位及提取方面有突出的优势[16]，它反映信息分布的均匀性，可描述系统的不确定程度[17]。因此，本文利用VMD算法对振动信号分解后，采用求取模态分量能量熵的方式构造特征量。

将断路器振动信号xm(t)的第n个IMF分量的包络An(t)按时间轴平均划分成R等份，并求取每段的能量值，计算公式如下：

(3)

其中，i=1,2,3,…，R，ti-1和ti对应第i段的开始时刻与结束时刻。

对Q(i)做归一化处理：

(4)

将归一化结果输入能量熵计算公式：

(5)

按上述公式分别对断路器正常状态、卡涩状态以及松动状态的能量熵进行计算。3种工况的部分能量熵值如表1所示。

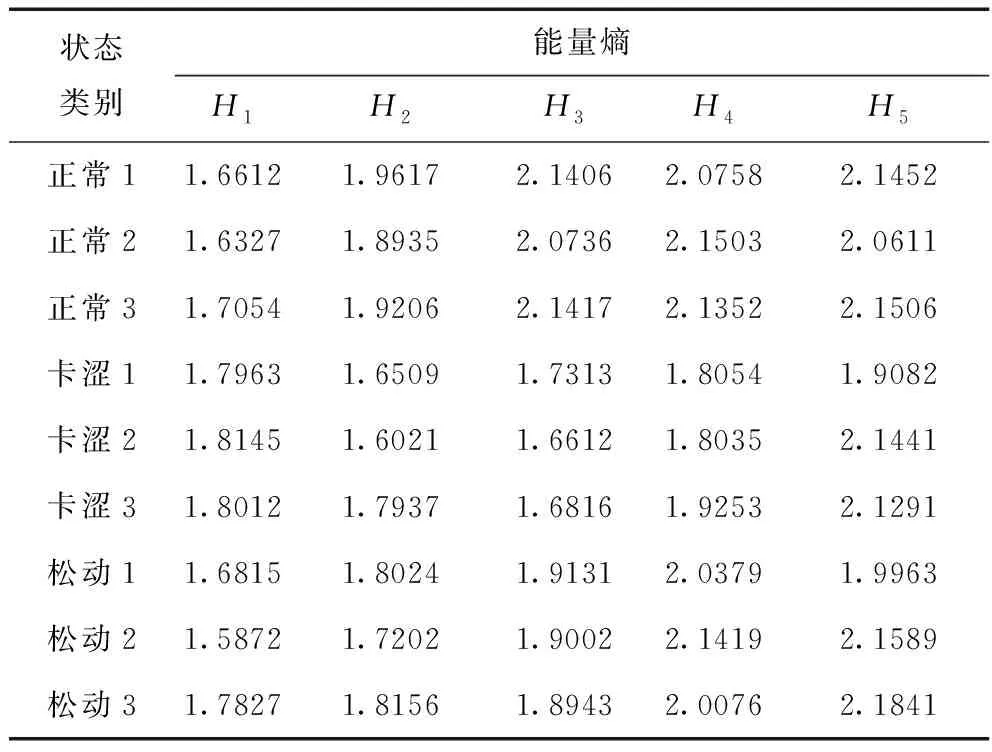
表1 VMD能量熵

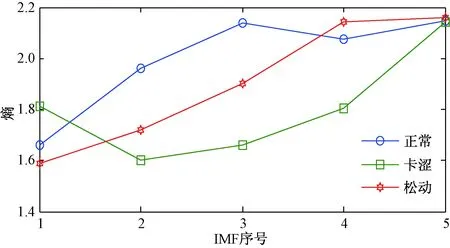
图6 各机械状态下VMD能量熵均值

断路器不同机械状态的振动信号差异较大，能量熵分布特征与断路器机械状态存在特定对应关系。由图6可知，卡涩状态熵值明显低于正常状态，且小幅低频振动的松动状态均值曲线与正常状态无明显重叠。故障状态新增事件使断路器能量分布产生较大差异，熵值纵差间隔明显，故障分类特征突出。

EEMD能量熵的均值分布如图7所示。

图7 各机械状态下EEMD能量熵均值

由图7可知，EEMD能量熵可将卡涩状态与正常状态有效区分，但松动状态与正常状态的能量熵均值曲线接近，交叉重叠现象严重，故障状态不易识别，特征提取效果不如VMD。

2.3 马氏距离

马氏距离(Mahalanobis distance)分类法是有效判断样本间相似程度的方法，它不受量纲影响，是基于统计学范畴的分类算法。在故障诊断的最后环节，本文将VMD能量熵构造的特征向量输入马氏距离判别器，以确定高压断路器的状态信息。

用T1、T2、T3代表断路器正常、传动机构卡涩及基座松动3种状态。在36组正常信号、30组传动机构卡涩信号及27组基座螺丝松动信号中，选取18组正常信号、15组卡涩信号及13组基座松动信号用于训练，其余用来测试。测试样本构建如表2所示。

表2 待测状态标号

断路器状态识别结果如表3所示。

表3 Mahalanobis距离判别器识别结果

识别结果表明，47组测试数据中仅有1处出现误判，误判原因在于基座松动属于低频小幅度抖动事件，不易与正常状态区分，且数据采集时因环境因素可能造成误差。但整体识别率高达97.62%，说明马氏距离判别器通过小样本即可实现断路器的机械故障诊断，过程简单，识别精度高。部分识别结果见表4， 其中，d1、d2、d3中最小判别距离对应的状态即为被测信号的故障类型。

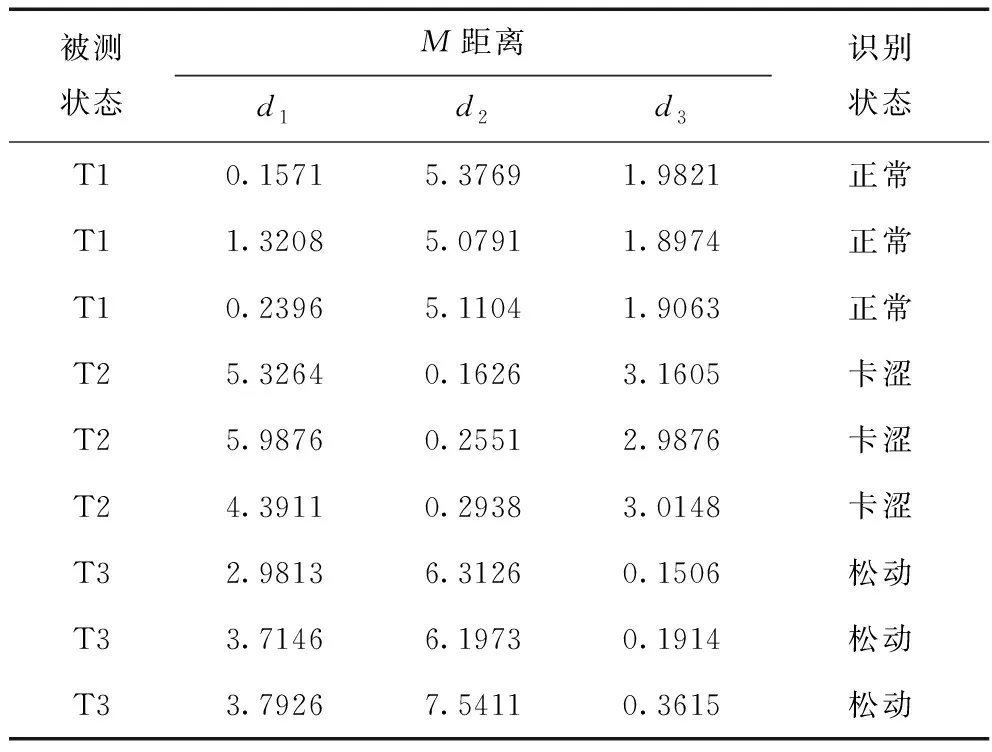
表4 部分识别结果

3 结论

(1) 振动信号监测电气设备状态信息，充分将传感技术、微电子技术、数字信号处理技术等融合在一起。断路器传统电气量方面的测量日渐成熟，振动监测相关领域问题亟待完善。

(2) 变分模态分解应用在断路器振动监测，一方面拓宽了算法本身的应用领域，另一方面为断路器机械故障诊断提供了新的研究思路。

(3) 能量熵反映信息的均匀性，信息分布越均匀熵值越大。断路器正常状态下信号波动小，分布均匀，熵值较大；故障状态时，振动信号各频段能量出现不同范围内的波动，各元素分布散乱不均，因而熵值较小；且相同状态熵值重复性明显，不同状态间熵值差异较大。实测信号特征与理论分析相符，以能量熵提取断路器故障特征参数具有较强的科学性及可行性。

(4) 基于量子粒子群改进的变分模态分解，优化了VMD参数设置问题，有效克服传统模态分解低噪声鲁棒性及模态混叠等缺点。将改进VMD能量熵与马氏距离相结合的故障诊断方式识别精度达到97.62%，具有较高的工程实用价值。

参考文献：

[1]万书亭, 肖珊珊, 豆龙江,等. 档杆故障下高压断路器弹簧操动机构应力分布研究[J]. 电力科学与工程, 2017,33(12):55-60.

[2]RUNDE M, OTTESEN G E, SKYBERG B, et al. Vibration analysis for diagnostic testing of circuit-breakers[J]. IEEE Transactions on Power Delivery, 1996, 11(4):1816-1823.

[3]常广, 王毅, 王玮. 采用振动信号零相位滤波时频熵的高压断路器机械故障诊断[J]. 中国电机工程学报, 2013, 33(3):155-162.

[4]CHARBKAEW N, SUWANASRI T, BUNYAGUL T, et al. Vibration signal analysis for condition monitoring of puffer-type high-voltage circuit breakers using wavelet transform[J]. IEEE Transactions on Electrical and Electronic Engineering，2012，7(1):13-22．

[5]孙一航, 武建文, 廉世军,等. 结合经验模态分解能量总量法的断路器振动信号特征向量提取[J]. 电工技术学报, 2014, 29(3):228-236.

[6]张佩, 赵书涛, 申路,等. 基于改进EEMD的高压断路器振声联合故障诊断方法[J]. 电力系统保护与控制, 2014, 29(8):77-81.

[7]HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition method and the Hilbert spectrum for nonlinear and non-stationary time series analysis[C]//Proceedings of the Royal Society of London Series A, 1998, 454:903-995.

[8]丁国君, 王立德, 申萍,等. 基于EEMD能量熵和LSSVM的传感器故障诊断[J]. 传感器与微系统, 2013, 32(7):22-25.

[9]李天云, 赵妍, 季小慧,等. HHT方法在电力系统故障信号分析中的应用[J]. 电工技术学报, 2005, 20(6):87-91.

[10]DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3):531-544.

[11]唐贵基, 王晓龙. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J]. 西安交通大学学报, 2015, 49(5):73-81.

[12]武小梅, 张琦, 田明正. 基于VMD-SE和优化支持向量机的光伏预测方法[J]. 电力科学与工程, 2017, 33(9):29-36.

[13]李万涛, 时献江. 基于VMD的轴承故障定子电流信号诊断[J]. 自动化与仪表, 2017(12):44-47.

[14]王晶. 基于VMD分解和小波阈值的语音信号去噪[J]. 软件导刊, 2017(10):12-14.

[15]许川佩, 胡红波. 基于量子粒子群算法的SOC测试调度优化研究[J]. 仪器仪表学报, 2011, 32(1):113-119.

[16]张小蓟, 张歆, 孙进才. 基于IMF能量熵的目标特征提取与分类方法[J]. 计算机工程与应用, 2008, 44(4):68-69.

[17]任玉卿, 王海瑞, 齐磊,等. 基于振动信号能量熵的轴承故障诊断[J]. 计算机应用与软件, 2017(9):283-287.