基于PSO-SVR的燃气轮机系统建模

刘延泉， 王如蓓， 杨 堃

(河北省发电过程仿真与优化控制工程技术研究中心

0 引言

长期以来，我国发电行业一直以煤炭为主要发电能源。但是近年来，环境污染问题日趋严峻，传统发电行业因其污染排放严重等问题遭遇发展的“瓶颈”，这与我国可持续发展的思想相违背[1]。因此，发电行业急需发展新能源来替代传统能源。燃气—蒸汽联合循环发电系统因其大大降低了污染排放等优点，在我国发电行业中所占的比重逐步提升。

燃气轮机是燃气—蒸汽联合发电机组的重要部分，建立燃气轮机系统的数学模型对于系统仿真、状态监控、故障检测等工作有着重要的意义。但燃气轮机系统是一个非线性、强耦合系统，这就增加了建立系统精确模型的难度[2]。支持向量回归机(SVR)的基本思想是统计学习理论，是近些年来发展较快的一种机器学习方法。与其他传统的回归算法相比，支持向量机的优点在于泛化能力强、不会陷入局部最优值和可以忽略模型内部结构等优点。支持向量机为系统辨识，模式识别等方面的问题提供了一种有效的方法，并可推广于预测和综合评价等领域和学科[3]。

1 燃气轮机系统输入输出参数

在燃气轮机的控制问题中，最重要的任务包括保持稳定的输出功率，同时保持排气温度在规定的范围内，以防止透平过热[4]。燃气轮机是燃气—蒸汽联合循环发电机组中最重要的设备，其中进入燃烧室的燃料量和进入压气机的空气量是燃气轮机部分的两个可调量。对于无补燃余热锅炉来说，其工作原理是利用燃机的高温排气对锅炉汽包内的水进行加热进而推动汽轮机工作，燃机排气参数的波动将直接影响余热锅炉的工作效率和机组整体性能[5]。从以上分析可知，控制燃机排气温度的稳定可以提高余热锅炉的运行性能。所以本文选择燃机功率和燃机排气温度为燃气轮机系统的两个研究对象，分析系统的输入变量与输出变量之间的关系。

压气机进口可转导叶系统除了可以在燃机启动和停机过程中防止喘振现象的发生，还可以在燃机正常运行时通过改变导叶的开度来改变压气机空气进气量。进入压气机空气体积流量的改变会使进入燃烧室的空气流量随之改变，从而改变燃烧室中天然气和空气的比例，使得燃机排气温度可以维持在较高的水平[6]。而在燃机启动和停机的过程中，IGV开度需要与压气机转速合理匹配以防止喘振现象发生而造成燃气轮机的损坏[7-9]。因此，燃机功率和透平排气温度除了与燃烧室的燃料量和IGV开度有关还与燃气轮机转速有关，本文选择的燃气轮机系统模型为一个多入多出模型，系统模型如图1所示。

图1 燃气轮机模型结构

2 支持向量机

2.1 支持向量回归机

与普通的线性回归问题一样，SVR模型的目的是寻找一个最优超平面，该平面与训练点的实际输出值之间的偏差不超过ε，同时函数模型输出曲线应尽可能的平坦。在求解最优超平面时，将求解目标转化为一个二次凸规划问题。但是实际问题中很多系统都是非线性系统，用一般的回归建模方法很难建立精度较高的非线性系统模型。SVR方法的优势在于可以将低维空间的非线性问题通过非线性映射转换成高维空间内的线性问题，降低建模的难度同时提高了建模的精度。因此，可以应用SVR方法解决样本空间中的高度非线性的问题[10]。

对于SVR问题，设数据样本为n维向量，l个数据样本表示为：

(x1,y1)，…，(xl,yl)∈Rn×R

(1)

式(2)所示为线性回归模型：

f(x)=ω·x+b

(2)

最优回归超平面转化为式(3)所示的二次凸规划问题：

(3)

约束条件为：

(4)

f(xi)-yi≤ξi+ε

(5)

式中：C为惩罚因子；ξ,ξ*分别表示松弛变量的上下限；ε为函数的拟合精度。

解决凸二次优化问题时，将问题转化成其对偶形式，计算时需引入拉格朗日函数，对于实际中非线性系统回归问题，选择合适的核函数K(x,y)将数据从低维空间映射到高维特征空间，在高维特征空间进行线性回归，其优化问题的对偶形式如式(6)所示：

(6)

此时：

(7)

支持向量回归模型表示为：

(8)

2.2 核函数选择及优化

常用的核函数有线性核函数，多项式核函数，RBF核函数以及多层感知机核函数等。对于核函数如何选择的问题，目前还没有合适的方法和定论。根据实验研究和经验通常情况下选择RBF核函数建模的效果更好。因对于燃气轮机系统内部机理相关知识匮乏，本文采用RBF核函数，核函数参数选择不同建模精度也不同，因此参数优化也是建模很重要的一步。RBF核函数如式(9)所示：

(9)

模型参数的选取对SVR模型的泛化能力有很明显的影响，主要影响参数包括惩罚因子C，拟合精度ε以及径向基函数宽度参数σ。惩罚系数C用来表示训练误差的大小和泛化能力的强弱，并且用来权衡损失和分类间隔的权重；拟合精度ε即样本逼近最优超平面的精度[11]。本文分别利用PSO算法和网格搜索法对SVR模型的参数进行优化。选取平均绝对百分误差(MAPE)来衡量SVR模型测试值与真实值之间的误差；选择均方根误差(RMSE)作为粒子的适应度值计算函数，其定义为：

1) 平均绝对误差：

(10)

2) 均方根误差：

(11)

式中：ai和ti分别是燃机排气温度或燃机负荷的真实值和预测值；n为预测数据的个数。

3 粒子群算法

3.1 PSO基本思想

PSO的基本思想是将优化问题的所有解构成一个粒子空间，粒子空间中的每个粒子都是优化问题的一个解。每个粒子都具有速度、位置及由目标函数决定的适应值，粒子在解空间中寻求最优的适应值。PSO首先对粒子群进行初始化，定义粒子的初始速度、位移并计算初始化粒子的适应值，然后通过迭代计算寻求目标函数解的最优值。粒子个体在搜索过程中适应值最优即个体最优值。整个种群在搜索过程中达到的最优解则为全局最优值。粒子靠着自身的记忆能力来完成更新。在每一次迭代中，粒子通过对比自身最优位置来更新个体最优值，并通过粒子空间中的全局最优值来确定下次搜索的方向并对全局最优值进行更新[12，13]。

3.2 标准粒子群算法

假设在一个M维的目标搜索空间中存在n个粒子，其中Xi=(xi1,xi2，…,xiM)，i=1,2,…,n表示第i个粒子的位置，Vi=(vi1,vi2,…,viM)为粒子的速度。计算出每个粒子的目标函数值即每个粒子的适应度值，对粒子的适应度值进行比较，选出最优值。对于目标函数最小化问题，目标函数值越小，对应的适应值越好[14-15]。

粒子i经历过的最优位置记为Xbest=(xi1,xi2,…,xiM),相应的适应值记为qbest,整个群体的最优位置记为Xbestg=(xg1,xg2，…,xgM),相应的适应值即全局最优解记为gbest。则粒子根据式(12)更新自己的速度：

Vim=ωVim+c1r1[Xbestm-xim]+

c2r2[Xbestgm-xim]

(12)

根据式(13)更新粒子的位置向量：

xim(t+1)=xim(t)+Vim(t+1)

(13)

式中：i=1,2,…,n；m=1,2,…,M；ω为惯性权值；c1表示认知因子；c2表示社会因子。xbest和xbestg分别代表向自身最优值和全局最优值更新时加速度权值，通常取2。r1和r2是0～1之间的随机数。

3.3 基于PSO优化的支持向量回归机

本文选择BPF径向基函数为核函数，以惩罚因子C和径向基函数宽度参数σ为优化对象，利用粒子群算法对SVR模型参数优化。与传统的网格搜索算法相比，粒子群算法能够有效地避免局部最优解问题，对目标参数进行全局寻优。对于小样本支持向量机回归问题，粒子群算法克服了传统优化算法运行时间长，优化步骤繁琐的缺陷。PSO优化步骤如下：

(1) 先从获得的样本数据向量集中筛选出支持向量构成样本训练集，训练样本集中的每个支持向量可以获得一组SVR模型的参数，每组参数构成一个粒子，所有粒子构成一个粒子种群。

(2) 选择均方根误差为粒子群的适应度函数，计算粒子群中各粒子的均方根误差。

(3) 种群初始化，包括初始化参数c1和c2，初始速度Vi以及粒子个体最优位置Xbest和全局最最优位置Xbestg等。

(4) 根据式(12)(13)对粒子的速度和位置进行更新。

(5) 计算新种群的适应度。

(6) 比较X0和Xbestg，若Xbestg优于前值则替换。

(7) 当迭代次数达到寻优设置的最大迭代次数或者获得了满足要求的粒子适应函数值时，终止迭代，否则返回第(4)步继续执行程序，直至满足精度要求或进化代数要求跳出循环。

4 基于数据的燃气轮机系统建模

4.1 数据预处理

本文的数据选自某燃气—蒸汽联合循环机组的历史数据。由于现场数据的直流或者低频成分会影响模型的精度。因此，要对数据进行高频滤波、剔除粗大值和数据归一化等预处理。

参数的量纲不同会影响模型的评价指标，因此要对数据进行归一化处理。数据经过归一化处理后便于对测试结果进行对比评价。数据归一化公式如式(14)所示：

(14)

其中，xmax和xmiin分别代表样本数据的最大和最小值。

式(15)为反归一化处理，测试数据的结果应该进行反归一化处理，便于对实验结果的直观分析。

x=xmin+x′(xmax-xmin)

(15)

4.2 实验仿真

以燃气轮机侧的功率和透平排气温度为研究对象。基于数据分析建立燃机负荷以及排气温度的SVR模型，并分别用粒子群算法和网格寻优算法对核函数的参数寻优，比较两种算法优化后的预测精度[15]。

(1)网格搜索法进行参数寻优的基本原理就是给定寻优参数的范围，通过穷举法寻找最优参数，并使用交叉验证来评估参数对模型性能的影响，以此选择出最佳的参数值。

本文采用K折交叉验证法(K-CV)对模型参数进行寻优，交叉验证方法的基本思想是将样本数据分成K组,将每组样本数据代入模型对模型进行验证,其余K-1组则对模型进行训练,K折交叉验证法可以得到K个模型,最终取验证集均方差的平均数作为SVR模型的性能指标[16]。

参数C和参数g的取值范围为[-4：0.2：4]，K=5，函数的拟合精度ε=0.01。本文选取预处理后的300组数据为训练样本，选择100组数据作为测试样本对模型进行验证。

图2所示为燃机功率SVR模型的平均绝对百分误差MARE=1.378 5%，最优参数C=4，g=1.319 5；图3所示为基于网格搜索的排气温度的SVR模型的平均绝对百分误差MARE=0.882 4%，最优参数C=4，g=1.319 5。

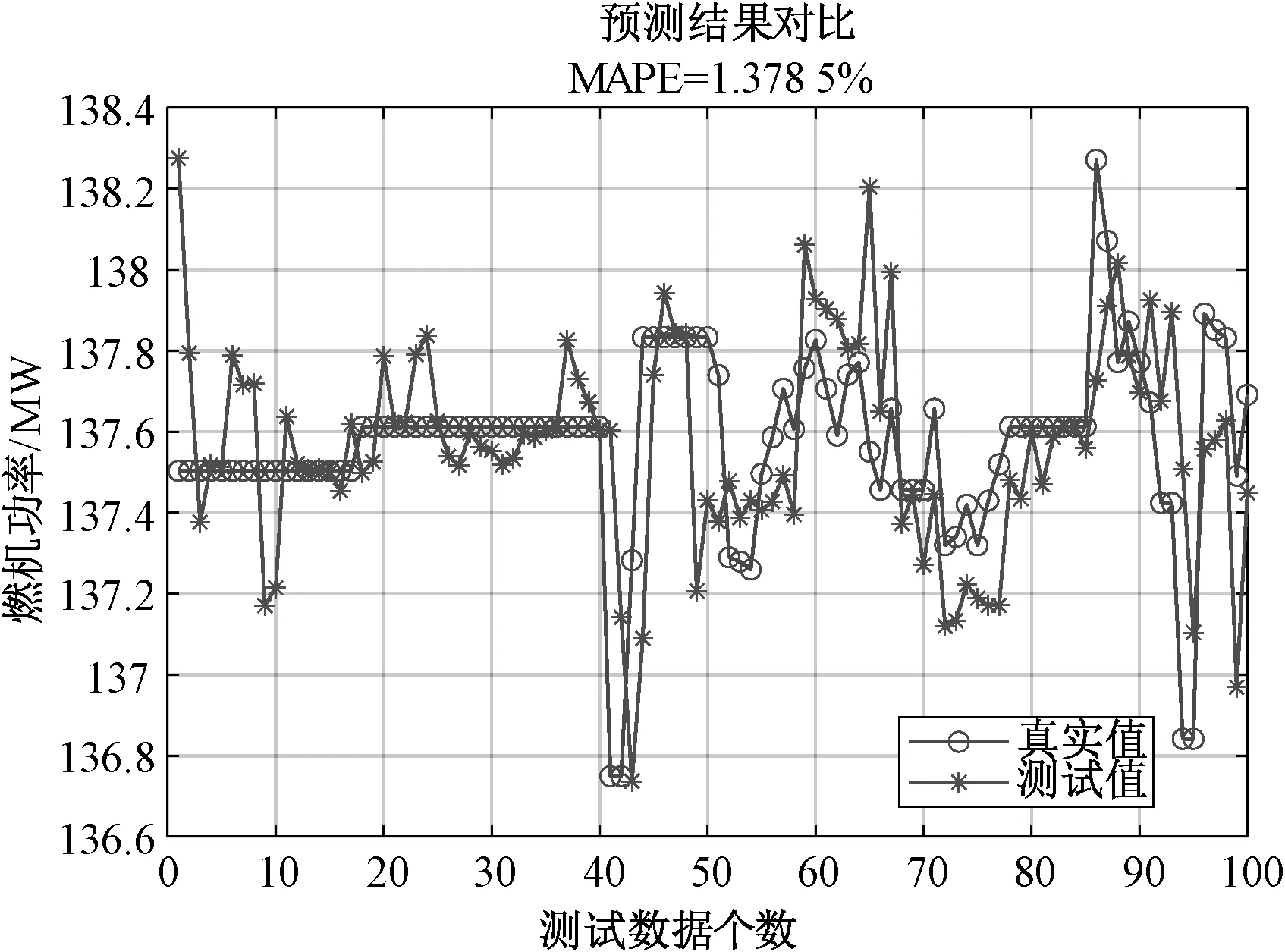
图2 网格搜索SVR模型燃机功率的测试值与真实值

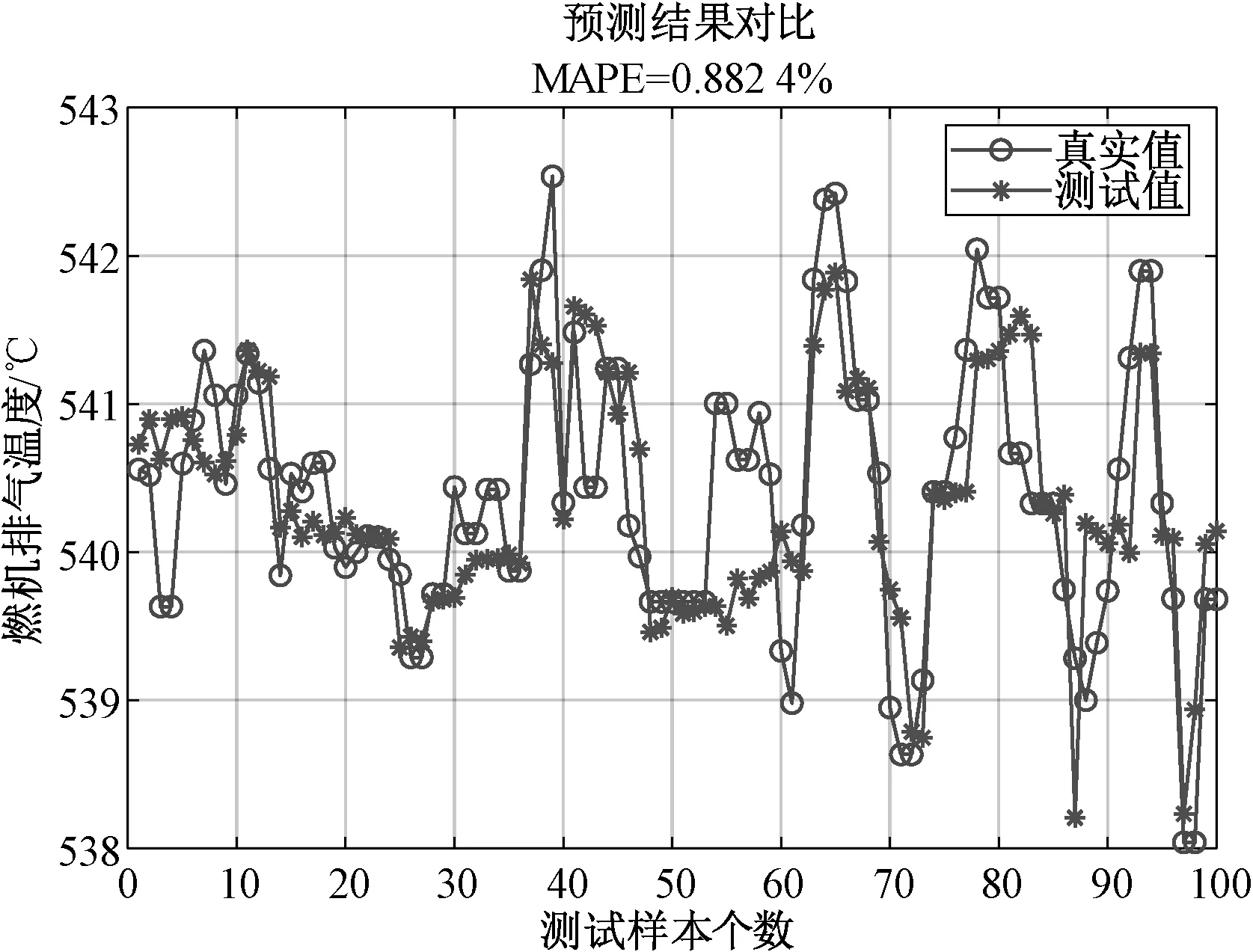
图3 网格搜索SVR模型燃机排气温度测试值与真实值比较

(2)基于PSO优化的SVR模型参数设置：种群粒子个数M=30；最大迭代次数Tmax=100；学习因子c1=c2=2；惩罚系数C和核函数宽度系数g的寻优范围为[0.1,10]。

图4所示为燃机功率SVR模型的平均绝对百分误差MARE=0.459 6%，最优参数C=6.608 6，g=1.340 7；图5所示为基于PSO优化算法的排气温度SVR模型的平均绝对百分误差MARE=0.397 5%，最优参数C=10，g=7.395 2。

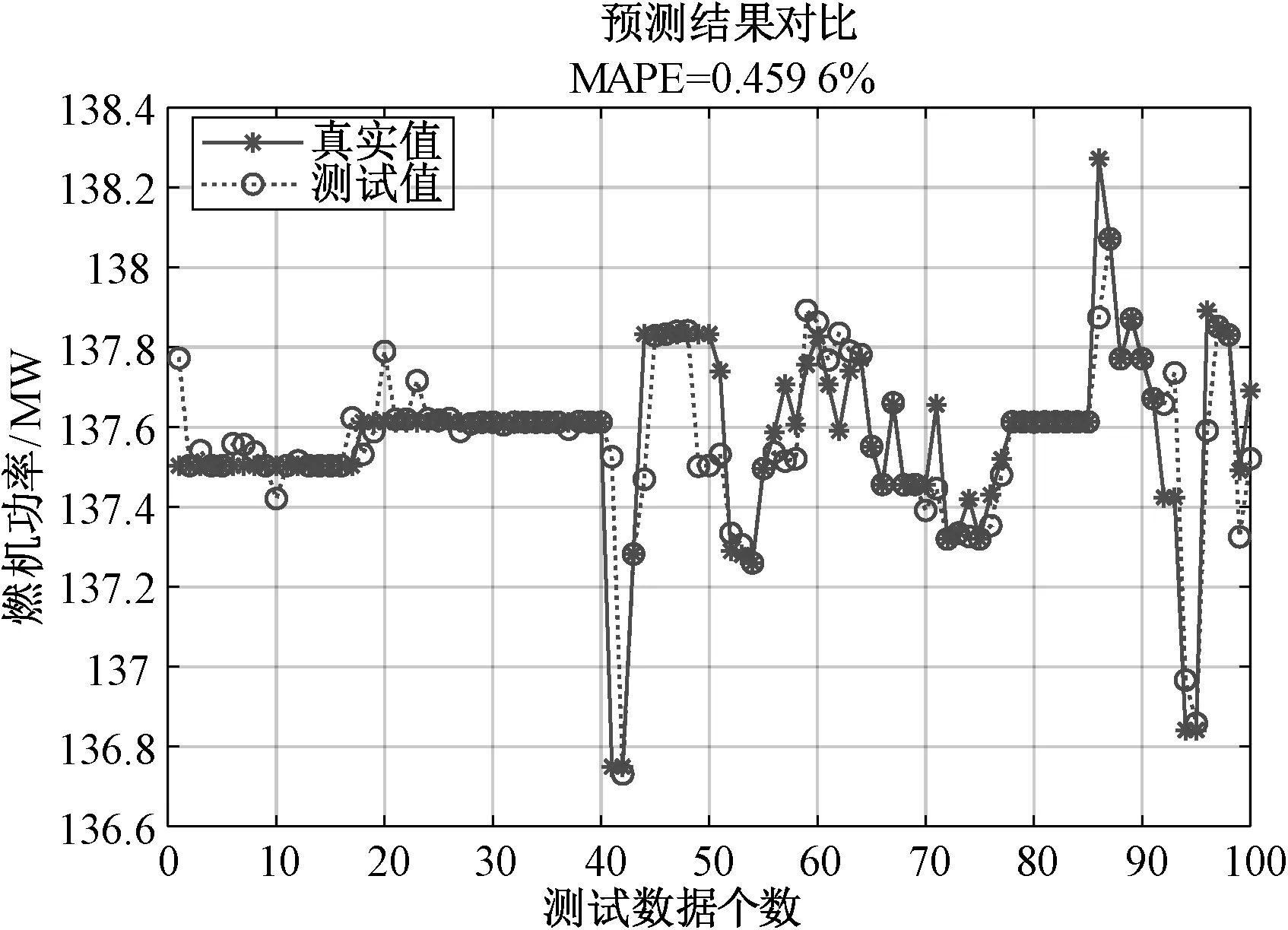
图4 PSO-SVR模型燃机功率测试值与真实值比较

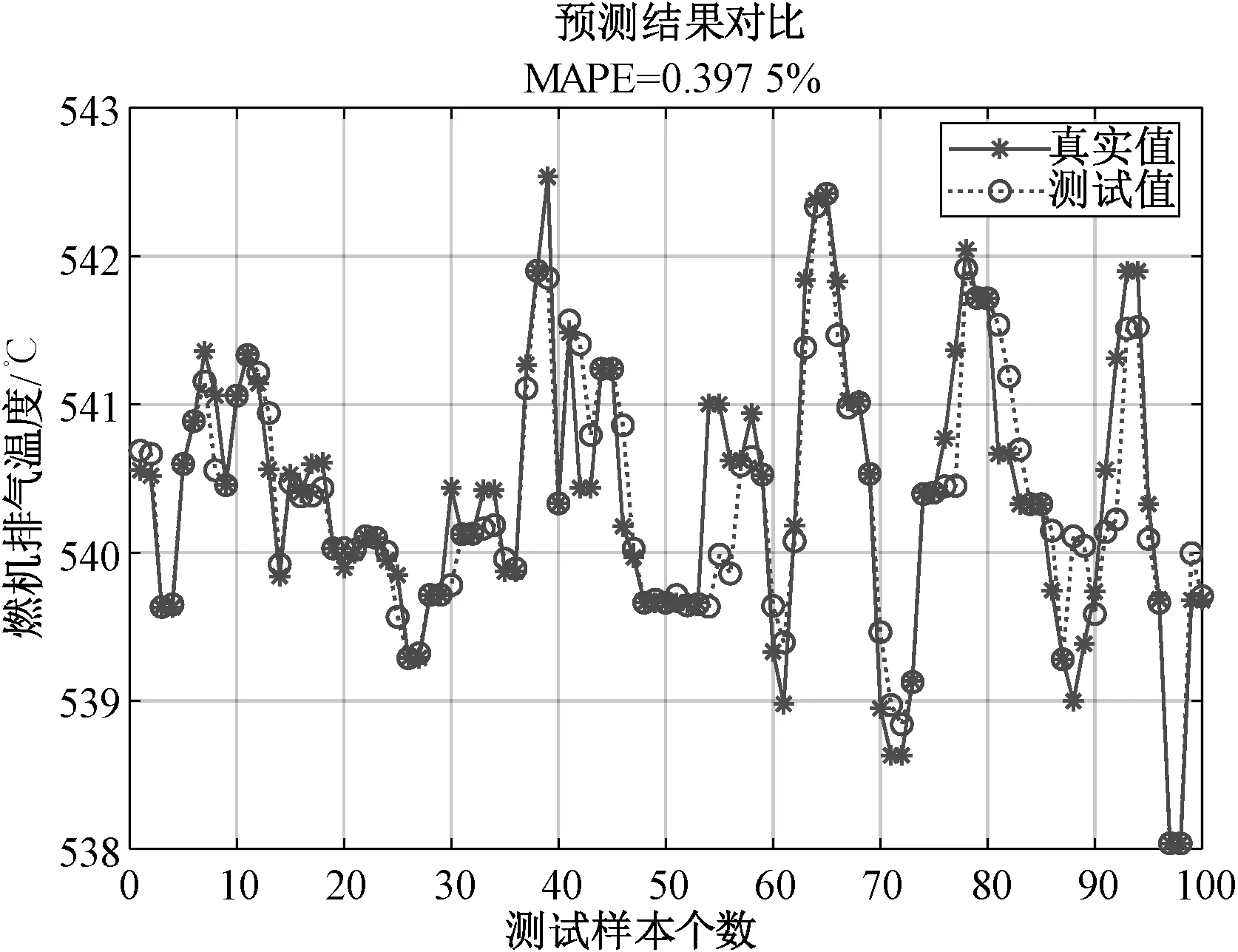
图5 PSO-SVR模型燃机排气温度测试值与真实值比较

图6所示为选择50组测试样本的燃机功率PSO-SVR模型的平均绝对百分误差MARE=0.435 8%，最优参数C=10，g=0.145 3。图7选择50组测试数据的基于排气温度PSO-SVR模型的平均绝对百分误差MARE=0.239 8%，最优参数C=0.230 6，g=2.839 1。

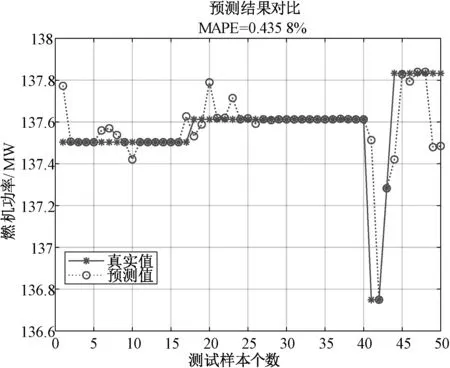
图6 测试样本个数对燃机功率PSO-SVR模型影响

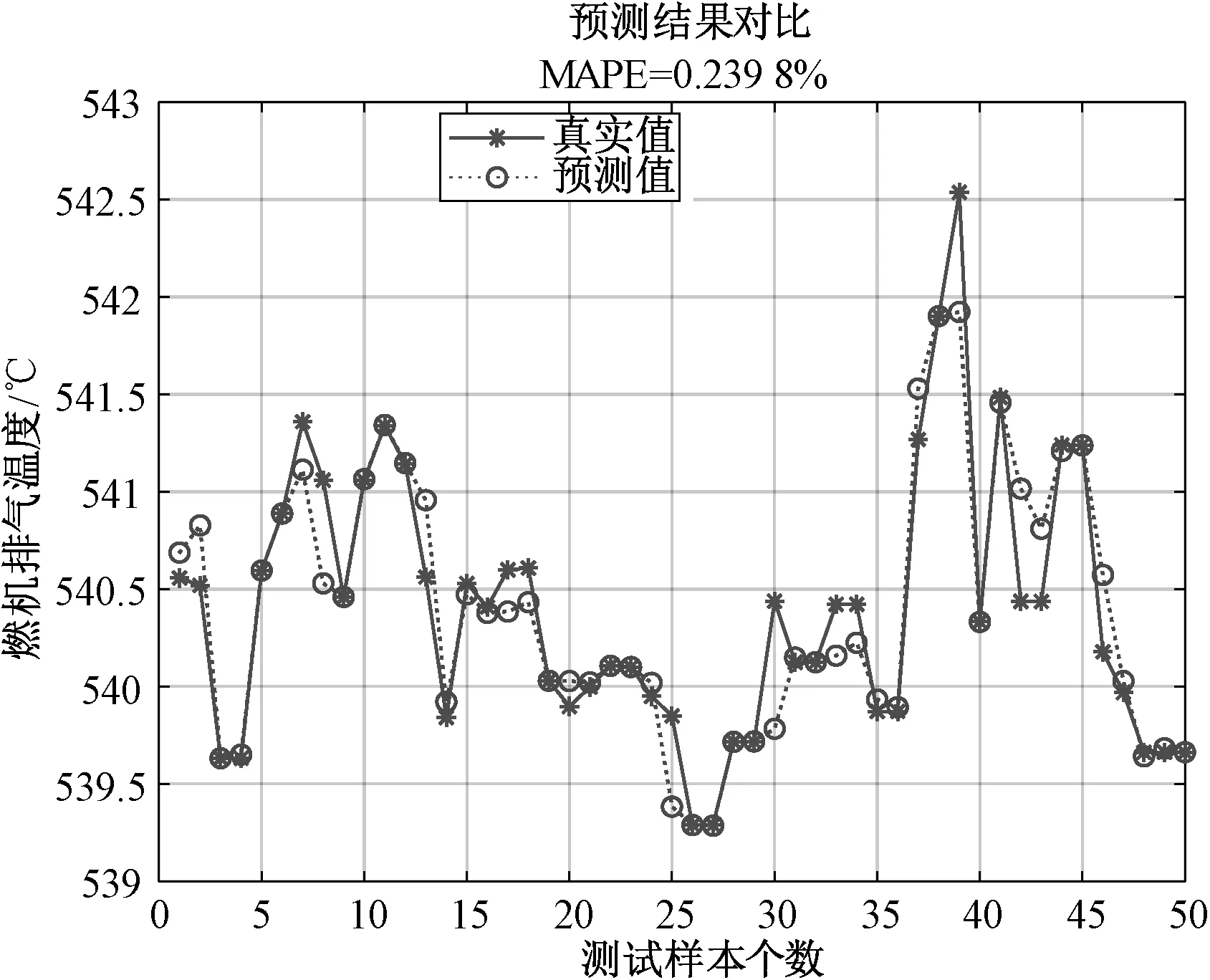
图7 测试样本个数对燃机排气温度PSO-SVR模型影响

结果分析：如图2和图3所示的基于网格搜索算法建立的SVR模型，从图中曲线可以直观地看出模型的测试值与真实值之间存在较大的偏差，拟合精度较差。如图4和图5所示的基于PSO优化算法的SVR模型，与网格搜索算法相比，PSO优化算法的SVR模型曲线拟合效果较好，提高了模型的预测精度且降低了运行时间。图6与图7为选择50组测试数据对SVR模型进行验证的结果，与选择100组测试数据对比可知，当测试样本数减少，运行时间降低且平均绝对误差减小。

5 结论

本文选取燃气轮机系统的燃机功率和燃机排气温度为研究对象，针对系统非线性，难建模的特点，提出了基于PSO算法优化的SVR模型对其进行建模研究，因为SVR模型不需要考虑模型内部各变量间的相互作用，只需确定系统的输入输出即可建立系统的回归模型。根据某燃气—蒸汽联合循环发电厂的现场数据，建立系统的SVR模型并进行MATLAB仿真，分析仿真结果可得PSO-SVR模型精度高于网格搜索法优化的SVR模型，基于PSO-SVR算法建立的燃气轮机功率和排气温度的回归模型具有更高的拟合精度。同时该算法还可用于系统的故障检测和短期电力负荷预测等方面。

参考文献：

[1]翁史烈，王永泓，宋华芬.现代燃气轮机装置[M].上海：上海交通大学出版社，2015：117-118.

[2]刘闯，金仁瀚，巩二磊，等. 多元线性回归方法预测燃气轮机发电机组性能[J].中国电机工程学报，2017，37(16)：4731-4738.

[3]刘苏苏，孙立民.支持向量机与RBF神经网络回归性能比较研究[J].计算机工程与设计，2011，32(12)：4202-4205.

[4]TARIK M H M，OMAR M，ABDULAH M F，et al. Modelling of dry low emission gas turbine using black-box approach [C]//Proc. of the 2017 IEEE Region 10 Conference，2017：1902-1906.

[5]高建强，张颖，陈鸿伟，等. 多元线性回归方法预测燃气轮机发电机组性能[J].动力工程学报，2011，31(4)：263-267.

[6]刘杨. 基于V94.3A型燃气轮机加速度不稳定状况研究与分析[J]. 电力科学与工程，2015，31(12)：52-60.

[7]刘微.基于燃气轮机的燃气蒸汽联合循环系统分析与建模[D]. 保定：华北电力大学，2015.

[8]陈梅珊，陈金伟，周登极，等.基于状态空间的燃气轮机建模与控制优化[J]. 热能动力工程，2016，31(2)：27-31.

[9]刘永葆，贺星，黄树红.基于改进遗传算法的燃气轮机自适应建模[J]. 航空动力学报，2012，27(3)：695-700.

[10]CHANG C C，LIN C J．Libsvm: a library for support vector machines[J]． ACM Transactions on Intelligent Systems and Tech- nology，2011，2(3): 27．

[11]蔡艳宁，汪洪桥，叶雪梅.复杂系统支持向量机建模与故障预报[M].北京：国防工业出版社，2015.

[12]闫国华，朱永生.支持向量机回归的参数选择方法[J]. 计算机工程，2009，35(14)：218-220.

[13]谷文成，柴宝仁，滕艳平.基于粒子群优化算法的支持向量机研究[J]. 北京理工大学学报，2014，34(7)：705-709.

[14]孙海蓉，谢碧霞，田瑶，等. 基于数据的SecRPSO-SVM 短期电力负荷预测[J]. 系统仿真学报，2017，29(8)：1829-1836.

[15]吴米佳，卢锦玲. 基于改进粒子群算法与支持向量机的变压器状态评估[J].电力科学与工程，2011，27(3)：27-31.

[16]李辉，俞进，李淑英，等.基于支持向量机的燃气轮机启动过程建模[J].燃气轮机技术，2012，25(1)：48-51.