考虑多方需求的电动汽车充电站规划研究

罗文雲， 周 浩， 于乐淘， 李金宝

(1.贵州大学 电气工程学院，贵州 贵阳 550025；2.中建三局一公司 安装分公司，湖北 武汉 430040； 3. 国家电网北京市城市照明管理中心， 北京 100078)

0 引言

自进入21世纪以来，全球经济高速发展，人们的生活水平有了质的提高，但是与此同时伴随着能源的消耗和环境的破坏，造成如今全球能源紧张和环境恶劣的局势。因此，如何节能减排、减少经济发展对能源的依赖和能源对自然环境的破坏成为各国迫切需要解决的问题。传统的燃油汽车同时作为能源消耗与产生废气的交通工具，其大量的使用是造成能源枯竭与温室效应的主要原因之一[1]。因此，具有能源利用率高、废气排放少和噪音小等优点的电动汽车可作为传统燃油汽车的替代品，缓解能源与环境等问题。大力推广电动汽车已成为各国能源发展战略的重要内容，也是汽车新兴产业的发展方向。而电动汽车充电基础设施的规划与建设是电动汽车发展与普及的前提。

国内外学者从电动汽车充电需求预测、电动汽车充电对电网影响和电动汽车充电选址定容等方面展开了大量研究工作。文献[2] 考虑了电动汽车用户充电行为的不确定性，分析了不同充电起始时间和充电持续时间对充电负荷时间分布的影响，结合电动汽车空间分布特性，搭建电动汽车时空分布充电负荷模型。文献[3] 分析了规模化电动汽车充电对配电网电压质量的影响，详细地分析了谐波污染、电压下降和三相电压不平衡问题，并提出了改善方法。文献[4]中提出一种基于云重心理论的电动汽车选址规划评估方法，综合考虑定性指标和定量指标，对候选站址方案进行评估，进而得到最优的选址方案。虽然以上文献对实际规划具有重要指导意义，但其忽略了在电力市场逐渐开放的时期，充电站的规划更应综合考虑投资方、电网运营方与用户方的需求。

本文首先从投资方，电网运营方与用户方三方面分析其对电动汽车充电站规划建设的需求，提出考虑多方需求的电动汽车充电站规划模型，采用粒子群算法与Voronoi方法对模型进行求解，算例仿真结果验证了该模型和算法的可行性与合理性。

1 电动汽车充电站规划的多方需求分析

1.1 投资方需求

作为电动汽车充电站建设运营的投资方，投资运营的经济性是其考虑的主要因素，也是电动汽车充电站规划的目标之一。合理的电动汽车充电站规划方案不仅使得投资方获得经济收益，还能促进电动汽车市场的良性循环，吸引更多的社会资本投入到电动汽车市场中，加快电动汽车产业的发展。因此，电动汽车充电站的规划需满足投资方的利益需求，应考虑充电站的运行收益、投资建设成本、运行维护成本以及充电站接入配网系统后引起的网络损耗成本，所以考虑投资方需求的充电站规划需尽量地提高运行收益，减少各项成本。

1.2 电网运营方需求

电动汽车充电站规划必须保证电网运行的安全性、供电的可靠性以及电能的质量。文献[5]分析了电动汽车充电站对配电网的影响，指出电动汽车充电站的建设导致电动汽车的聚集充电，此行为将影响配电网负荷平衡，造成部分地区负荷紧张，同时电动汽车充电行为所导致负荷的时间分布与叠加将加重配电网负荷峰谷差。此外，电动汽车充电站的接入也将对电网节点电压造成影响，降低电能质量，影响用户正常用电。因此，对于电网运营方，电动汽车充电站的规划必须以电网安全运行为前提，在此前提下考虑充电站建设的投资经济性。

1.3 用户方需求

对于电动汽车的使用者来说，电能就是他们所购买的产品。电能作为一种特殊商品，除了要求保证满足用户的商品质量和需求量以外，其用户使用体验的满意度也是十分重要的。令人满意的使用体验不仅会增加用户的回购率，还促进该产品的普及。因此，电动汽车充电站的规划需满足电动汽车用户的负荷需求和提高用户对于充电服务的满意度。该满意度一方面从用户充电服务所消耗的时间来考虑，另一方面从用户充电路上的电能损耗成本来考虑。

2 数学模型

在普及电动汽车和建设电动汽车充电站的初期阶段，政府作为充电站投资建设和运营管理的主导者，其主要目的是推广电动汽车，因此充电站规划大多以建设成本最小化作为目标函数，只考虑了其建设经济性。但随着电动汽车的发展，要使充电站规划建设市场化，则需综合地考虑市场需求与投资收益性，提高充电站的市场竞争力。

2.1 考虑多方需求的电动汽车充电站规划模型

如前面所述，考虑多方需求的电动汽车充电站规划将从投资方、电网运营方和用户方进行分析，建立满足三方需求的规划模型。其中，将投资收益与用户满意度作为充电站总收益，以总收益最大化作为目标函数，模型如下所示：

maxF=C+T

(1)

式中：F为充电站总收益；C为充电站投资收益；T为用户满意度。

2.1.1 充电站投资收益

投资方是否决定投资建设充电站，主要看重其投资收益率，投资收益率越高，投资者越多，充电站与电动汽车的普及越快。因此，在由政府主导的充电站建设初期阶段之后，由市场主导的充电站规划建设应以其投资收益最大化为目标，建立以充电站年投资收益最大化的目标函数，其模型如下所示：

C=max(C1-C2-C3-C4-C5)

(2)

式中：C为充电站投资收益;C1为充电站年售电收入；C2为充电站年购电成本；C3为充电站年建设运行成本；C4为充电站购地成本；C5为年网络损耗成本。

(1)年售电收入

充电站为电动汽车提供充电服务，售电费用与充电单价和充电量有关。根据电动汽车充电负荷计算方法，采用单台电动汽车一天24 h内的平均充电负荷来计算每个充电站在规划区域内的充电容量，进而求出每个充电站一年的售电收入，其表达式如下所示：

(3)

式中：N为充电站数量；Pi为第i座充电站的规划充电容量；csi为第i座充电站向用户售电的价格。

(2)年购电成本

充电站需向售电方购电，按照购电单价和购电量收取购电费用。同样根据电动汽车充电负荷计算方法，采用单台电动汽车一天24 h内的平均充电负荷来计算每个充电站在规划区域内的充电容量，进而求出每个充电站一年的购电成本，其表达式如下所示：

(4)

式中：N为充电站数量；Pi为第i座充电站的规划充电容量；cpi为第i座充电站向用户售电的价格。

(3)年建设运行成本

投资者新建充电站的年建设运行成本分为两部分：年建设成本与年运行成本。其中年建设成本是指固定成本和等效投资成本，年运行成本是指与充电设施配套的设备维修成本、折旧成本和人工工资等。文献[6]中将各项成本折算到单台充电机上，即年建设运行成本均为充电机的函数，表达式如下所示：

(5)

式中：ni为第i座充电站内充电机数量；φi(ni)为第i座充电站的年建设成本；ψi(ni)为第i座充电站的年运行成本；τ为运行年限；W为充电站固定成本，即修建成本；q1和q2分别为充电机单价和与充电机台数有关的等效投资因子。

(4)购地成本

充电站规划建设的位置决定了其购地成本。根据城市里各区域用地性质和功能的不同，可将城市土地大致分为商业用地、居民用地、工业用地、教育用地和物流用地5部分，具有不同的土地价格。

充电站建设的占地面积与充电站规模有关，充电站规模越大，充电机数量越多，则占地面积越大。同理，充电站建设之后，其建设可以长期使用，其规划有一定的目标年限，在运行的时间内，平均摊到每一年的购地成本表达式如下所示：

(6)

式中：μi为第i座充电站建设位置的土地价格；s为单套充电机占地面积；S0为其他设备占地面积。

(5)全年网络损耗成本

电动汽车充电站接入电网后，改变了电网功率分布，引起网络功率损耗，通过牛顿拉夫逊法对配电进行潮流计算，得出有功功率损耗数值，由下式计算得出损耗成本，该部分的费用由投资方支付给电力公司，即：

(7)

式中：α单位网络损耗成本；Ploss为新建充电站引起的总有功功率损耗。

2.1.2 用户满意度

“用户满意度”这一概念，最初由R．L．Oliver等提出，是指用户对产品本身和在享受服务过程中的整体感受，表达的是用户在此过程中的一种感知心理[7]。在中国电力市场逐渐开放的趋势下，产品质量不再是市场单一的需求，用户对产品使用的满意度已成为决定企业利润的重要因素。特别是电能这一独特的产品，在目前供大于求的阶段更需要多样化的市场模式来推动消费。伴随电动汽车的发展，电动汽车充电站的规划必须考虑用户的满意度，提高用户在享受充电服务过程中的满意度，进而促进提高用户使用电动汽车的频率。

电动汽车充电服务的满意度体现在用户对完成充电过程所消耗的时间和用户行驶到充电站过程消耗的电能，即用户充电路上成本。建立以用户满意度最大化为目标函数的模型，其表达式如下所示：

T=max(T1+T2)

(8)

式中：T1为时间满意度；T2为成本满意度。

(1)时间满意度

由于每个人对时间的敏感度不一样，当超过用户所能接受的最长时间时，其产生的满意度会呈现不同的情况，文献[8～10]中指出，用户对时间的满意度会呈现凹凸性，此现象称之为凹凸时间满意度，其表达式为：

(9)

式中：u(tij)为时间满意度刻画函数；tij为第j个用户从需求点行驶至距离最近的充电站i的时间；Umax为顾客满意所接受的最长时间；TL为顾客不满意的最短时间。ω为时间敏感系数，。

根据以上分析，电动汽车用户充电服务的时间满意度函数如下所示：

(10)

式中：N为充电站数量；M为电动汽车数量。

(2)成本满意度

自用户产生充电需求时，其从所在位置出发前往至充电站，这段路程除了消耗时间，还会消耗电能。在不是特别需要补充电能的情况下，如果前往充电站的成本太高，选择充电的用户相对减少。因此，对于充电路上成本的接受程度，将影响用户是否选择充电。合理的电动汽车充电站规划方案会提高用户对于成本的满意度，满足用户充电需求。

用户在充电路上消耗的电能所产生的成本与用户产生充电需求的所在位置到充电站的距离有关,同时也与各类型汽车的每公里耗电量有关。假设在每次充电的过程中，用户都会选择离当前距离最近的充电站充电，其所行驶距离用充电站的欧式距离来度量，其表达式如下所示：

(11)

式中：Lij为第j辆车产生充电需求时，其所在位置到充电站i的距离；xj,yj表示第j辆车产生充电需求时所处位置的横纵坐标；xi,yi表示充电站i所处位置的横纵坐标;λij为充电需求点到充电站i的道路曲折系数。

则用户一年在充电路上消耗电能的成本，由下式计算：

(12)

式中：C(Lij)为用户充电路上年损耗成本；h为电动汽车每公里耗电量；csi为第i座充电站向用户售电的价格。

由上式可以看出，在每公里耗电量一定的情况下，用户充电路上消耗电能的成本与Lij成正比，距离越近，成本越低，距离越远，成本越高。因此可将用户对成本的满意度折算成用户对Lij的满意度。

与时间满意度相似，对于距离的长短，人们心里的接受程度也不一样，当超过用户所能接受的最远距离时，其产生的满意度也会呈现不同的情况。因此，本文采用调查问卷方式，对83名不同年龄层的用户进行了问卷调查，针对于用户对充电站可接受距离的调查结果如表1所示。

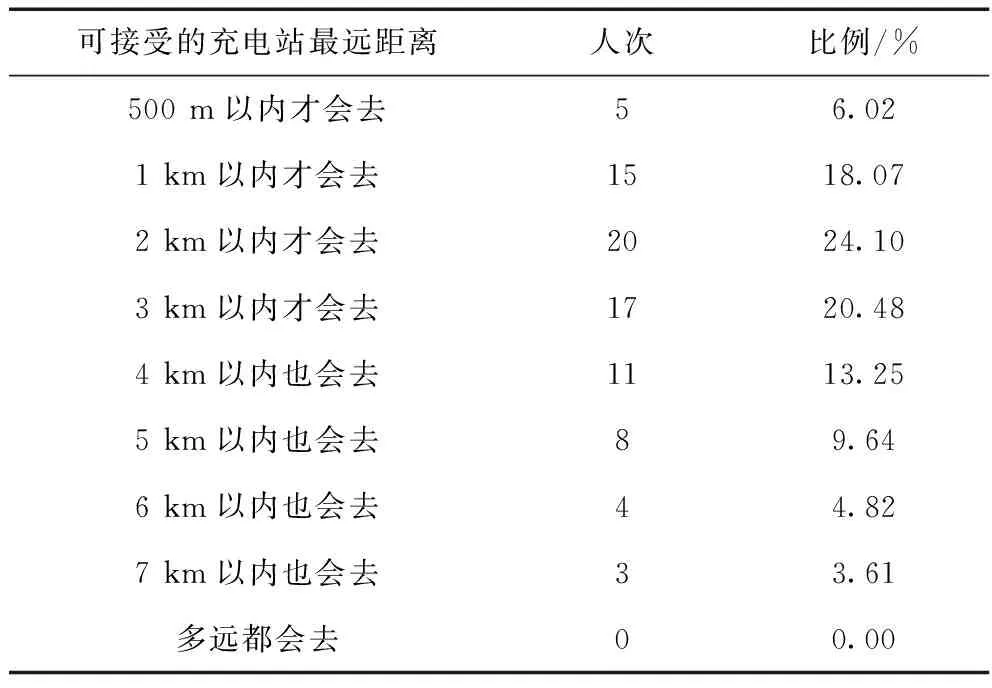
表1 用户可接受充电站最远距离调查统计表

由表1可知，70%左右的用户可接受充电站的最远距离在3 km以内，随着距离的增加，选择充电的用户逐渐减少。将数据进行线性拟合，得到如图1所示的函数图。

图1 用户可接受充电站的最远距离拟合函数图

根据上述分析可以得出，用户对于充电站最远距离的接受度随着距离的增加而降低，满足以下公式：

v(Lij)=(p1Lij4+p2Lij3+p3Lij2+p4Lij+p5)/100

p1=-0.115 9;p2=2.284;p3=-15.33;

p4=37.41;p5=-13.14

(13)

式中：v(Lij)为成本满意度刻画函数；Lij为第j辆车产生充电需求时，其所在位置到充电站i的距离。

因此，用户对于成本满意度函数如下式所示：

(14)

式中：N为充电站数量；M为电动汽车数量。

2.2 约束条件

2.2.1 电网安全性约束

如前所述，电动汽车接入电网会对电网造成一定的影响，为保证电网运行安全可靠，需满足以下约束条件:

(1)接入节点电压偏移量的约束

Umin≤Ul≤Umax

(15)

式中：Umin为配电网节点l所需满足的电压偏移量的上界;Umax为配电网节点l所需满足的电压偏移量的下界。

(2)充电站接入点准入容量约束

Piltotal≤Pjmax

(16)

式中：Piltotal为接入配电网节点l的充电站i的容量，主要由充电设备的数量与输出功率决定；Pjmax为电网节点l所允许接入的最大功率，主要由节点l处的负荷大小和线路的传输能力决定。

2.2.2 用户充电负荷需求约束

电动汽车充电站的额定容量应满足区域范围内电动汽车用户的充电负荷需求，其额定容量应不小于每天的最大充电负荷需求。

(17)

式中：Pi为第i座充电站的规划充电容量；Pj为第j辆车的充电负荷需求；ρ为最大充电负荷需求与总充电需求量之间的折算系数。

2.2.3 充电站服务半径约束

为了避免充电站之间距离太近造成资源浪费，也避免充电站太远，达不到合理规划目的，因此充电站服务半径约束为：

0.5R≤D≤R

(18)

式中：R为区域内充电站最大充电服务半径；D为充电站服务半径。

3 模型求解

采用粒子群算法[11]寻找最优的充电站位置及其容量、充电机数量。并采用Voronoi方法[12]实现充电站服务范围的划分，并将区域内充电负荷需求点分配到各个充电站的服务范围内，得到各充电站的容量分配数据。其具体规划思路如下：

(1)确定区域内电动汽车充电负荷需求。假设规划区域内总充电负荷需求，并生成一定数量的充电需求点位置与需求量。

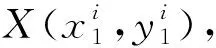
S={(x1,y1),(x2,y2),…，(xNC,yNC)}

(19)

则粒子的2NC维空间坐标为：

X=[x1x2…xNCy1y2…yNC]

(20)

(3)划分服务范围。采用Voronoi方法实现充电站服务范围的划分，并将区域内充电负荷需求点分配到各个充电站的服务范围内，得到各充电站的容量分配数据。

(4)以总收益最大为目标，寻找充电站最优位置。以提出的目标函数作为适应度函数，计算各粒子适应值，通过计算，得到并记录个体极值和全局极值。

(5)更新粒子速度与位置，并编译为新的充电站站址坐标，循环至(3)。通过反复计算，直至满足最大循环次数，得到计算结果，并根据约束条件进行可行性分析，得到最终输出方案。

使用粒子群算法求解流程图如图2所示。

图2 模型求解计算总流程图

4 算例分析

为验证本文所述的考虑多方需求的电动汽车充电站规划模型的可行性与有效性，假设规划区域为如图3所示的一个城市区域，该区域面积为9×9(km2)，将其对象到坐标轴中的区域为[0≤x≤9,0≤y≤9]，细分为9个不同类型与功能的子区域，具体位置分布如图3所示。

图3 规划区域图

每种类型的用地具有不同的土地价格，其具体价格如表2所示。

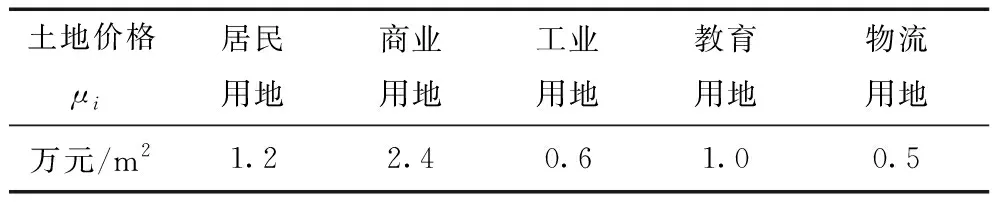
表2 土地价格表

假设该区域内电动汽车总的充电需求量为 39 279.063 kW·h，电动汽车共有900辆，其中公交车250辆，私家车350辆，出租车300辆，并用MATLAB软件在规划区域内生成900个点代表充电负荷需求点的位置，每个点对应一个充电需求量。

本文采用文献[13]中IEEE33节点标准配电网络，将规划区域标注具体坐标，并将配网系统拓扑图与规划区域图结合,如图4、图5所示，粗线部分为配网线路。

图4 IEEE33节点配电系统拓扑图

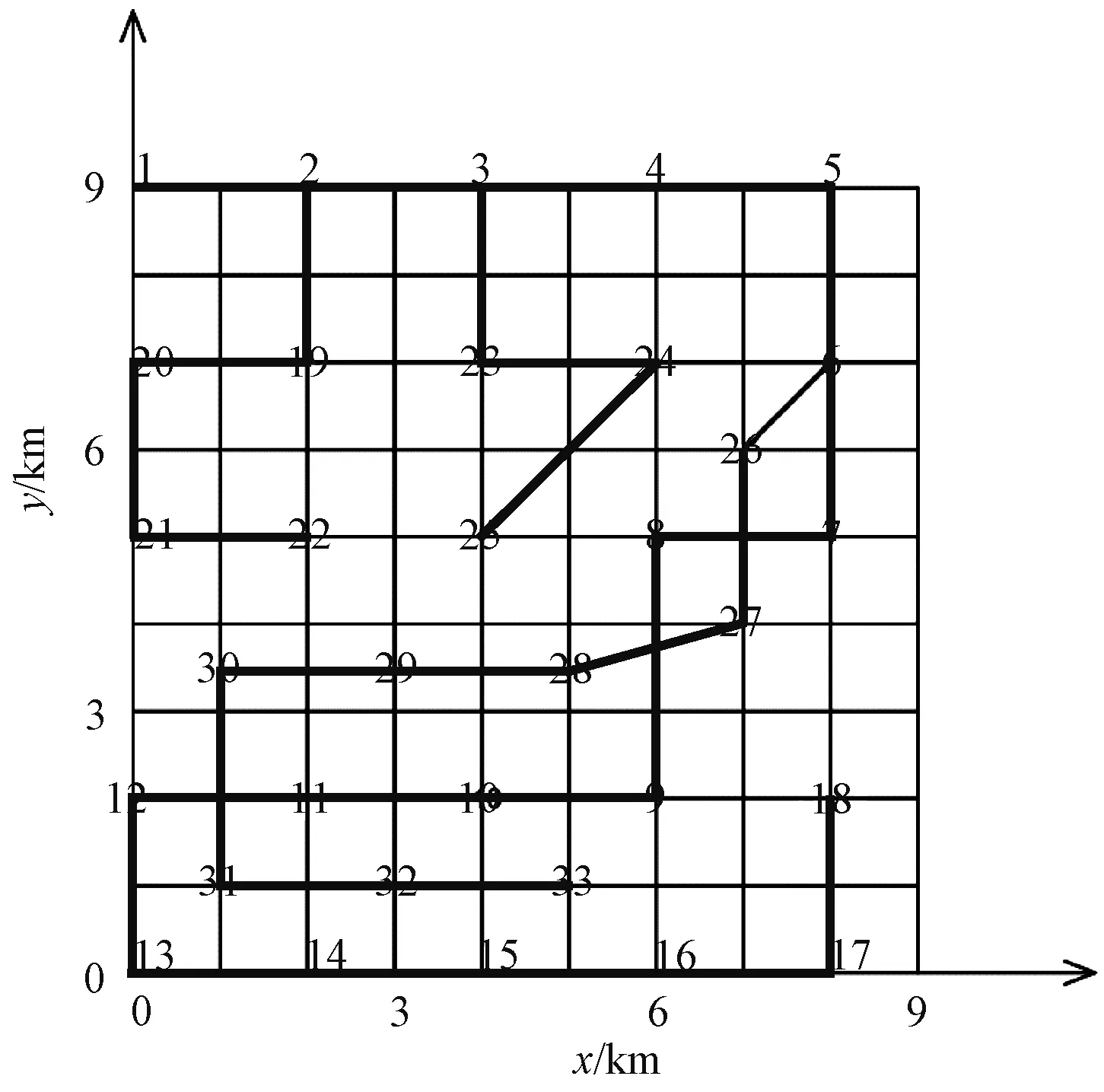
图5 规划区域配网图

查阅相关资料后，在本文建立的考虑多方需求的模型中的其余参数，如表3所示。

表3充电站规划参数值

本文使用粒子群算法的过程中，设置最大循环次数K为1 000，粒子数NC为30。学习因子c1和c2也称加速常数，根据经验，通常c1=c2，本文取2.0。惯性权重ω的大小决定了对粒子当前速度继承的多少，一般取0.6～0.75之间，本文取0.72。通过计算，各规划方案的总收益如图6所示。

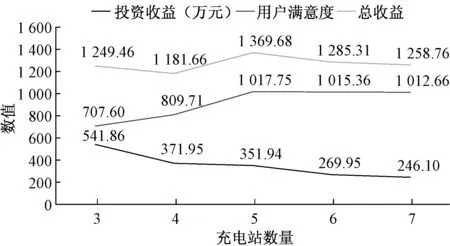
图6 各规划方案总收益图

由图6可以看出，随着电动汽车充电站数量的增加，各项成本也相应增加，投资收益随着充电站数量的增多而减少，成线性递减趋势。随着充电站数量的增加，用户在充电路上花费的时间与消耗的成本越来越少，因此用户满意度随充电站数量的增加而增加，而当N≥5，用户对于时间与距离的敏感度相差无几，因此用户满意度递增趋势减缓，趋于稳定。通过上述计算结果得出，当N=5时，考虑多方需求的电动汽车充电站总收益最大，将该方案进行接入电网的安全性校验与修正，在配电网中选取距离充电站站址最近的节点作为接入点，根据前述IEEE33节点配网负荷数据，采用牛顿拉夫逊法进行潮流计算，得出各节点电压幅值，校验与修正后的接入方案为[11 25 15 24 9]号节点。其优化配置结果如表4所示。规划布点方案图如图7所示。

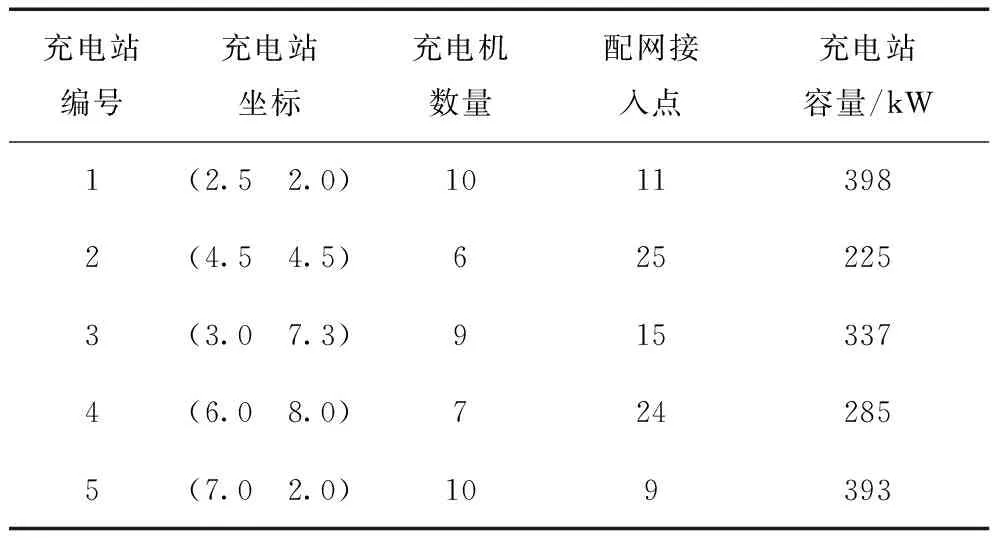
表4 充电站优化配置结果

图7 N=5时充电站规划布点方案图

5 结论

电动汽车充电站的规划建设是目前推动电动汽车发展的至关重要的环节。电动汽车充电站的规划不仅需要考虑投资方对充电站投资收益的需求，还需考虑电网运营方对电网安全运行的需求与用户方对充电服务满意度的需求。因此本文综合考虑了以上三方对充电站规划的需求，建立了考虑多方需求的电动汽车充电站规划模型。将充电站投资收益与用户满意度的和作为充电站的总收益，以总收益最大化为目标函数，采用粒子群算法和Voronoi方法得出优化结果即充电站最优配置。通过算例实验分析，证明了该模型具有可行性，能满足各方的需求，更具合理性。

参考文献：

[1]何战勇.电动汽车充电站规划方法及运营模式研究[D].北京：北京交通大学,2012.

[2]刘晓飞,崔淑梅,谢富鸿,等.基于停车需求模型的电动汽车V2G放电负荷时空分布预测[J].电气工程学报,2015,10(8):22-28.

[3]宋辉,徐永海. 规模化电动汽车充电对配电网电压质量的影响及其对策[J]. 现代电力, 2017(3): 30-35.

[4]彭泽君,兰剑,陈艳,等.基于云重心理论的电动汽车充电站选址方法[J].电力建设,2015,36(4):1～7.

[5]高赐威,张亮.电动汽车充电对电网影响的综述[J].电网技术,2011,35(2):127-131.

[6]熊虎,向铁元,祝勇刚,等.电动汽车公共充电站布局的最优规划[J].电力系统自动化,2012,36(23):65-70.

[7]OLIVER R L, BURKE R R. Expectation processes in satisfaction formation: A field study[J]. Journal of Service Research, 1999, 1(3):196-214.

[8]孙琼玲. 基于时间满意度的时装业配送车辆调度研究[D]. 南京：南京财经大学, 2011.

[9]LI D, KANG X H, YAN X T. A model for supply chain critical facility protection planning based on time satisfaction[C]. Intelligent Computation Technology and Automation, 2009.

[10]马云峰. 网络选址中基于时间满意的覆盖问题研究[D]. 武汉：华中科技大学, 2005.

[11]KENNEDY J, EBERHART R．Particle swarm optimization[C]//Neural Networks, IEEE International Conference on. IEEE，1995：1942-1948.

[12]葛少云，李慧，刘洪．基于加权Voronoi图的变电站优化规划[J].电力系统自动化，2007，31(3):29-34.

[13]BARAN M E,WU F F．Network reconfiguration in distribution systems for loss reduction and load balancing[J]．IEEE Transactions on Power Delivery，1989，4(2): 1401-1407．