基于动态时间规整算法的纵波与转换波时间域匹配
2018-07-03张一琛陈双全靳松李向阳
张一琛 ,陈双全 *,靳松 ,李向阳 ,
1 中国石油大学(北京)油气资源与探测国家重点实验室,北京 102249 2 中国石油大学(北京)CNPC物探重点实验室,北京 102249 3英国联邦地质调查局(BGS),爱丁堡 EH14 4AP
0 引言
多波地震勘探技术能够采集到更加丰富的地震波场信息,并能利用多波地震数据的走时、振幅、以及纵、横波之间的时差、速度比和其他各向异性参数,对油气藏的岩石物性和流体性质进行更为精确的成像描述,从而最大限度地消除单一纵波储层预测的多解性,提高非构造油气藏探测精度,有助于研究穿透气云的成像和预测裂缝的发育程度[1-2]。目前,多波地震勘探主要是利用转换波数据与纵波数据进行联合反演与解释,开展油藏的储层描述与油气检测。其中多波地震勘探的一个重要环节是纵波与转换波数据在不同时间域的匹配处理,这是纵波与转换波资料进行联合反演与解释的关键一步。纵波与转换波数据匹配效果的好坏和精度的高低将直接影响后续多波联合反演与解释的效果。
早期的纵波与转换波数据的匹配主要是依靠人工层位标定法。解释人员结合测井资料进行地震剖面的层位标定,通过对比相似的反射层位来匹配同相轴。然而该方法具有极大的局限性,仅能适用于地层反射特征明显的区域,一旦地层构造复杂,反射波特征不明显时,匹配结果就会出现较大的随意性和误差。
之后,为了尽量避免在数据匹配过程中的人为因素的干扰和误差,研究人员提出了利用纵波与转换波数据的运动学与动力学特征进行基于数据处理的匹配方法。该类方法的主要思路是先给出初始纵横波速度比模型,然后结合相关性来校正模型或者利用最小二乘等迭代方法更新速度比模型,之后再凭借精确的速度比模型将转换波匹配到纵波时间域。Gaiser(1996)利用纵横波速度比(γ0)和最大相关法[3]进行多波资料匹配,Chan(1998)对常数γ0值多次试验修正后实现时间对数域纵横波匹配[4],该匹配方法只适应于特定目的层。Van Dok和Gaiser等(2001)利用最大相似性原理[5],扫描纵波与转换波资料的γ0谱,拾取平均γ0值来匹配图像。Garotta等(2002)通过相关求取纵横波速度比[6],在时间域匹配纵波与转换波。Fomel等(2003)利用最小二乘法优化全局最优解来实现纵横波自动匹配[7]。Van Dok和Kristiansen(2003)通过手动拾取具有明显地质特征的层位实现时间域的大致匹配[8]。Nahm等(2003)通过对准主要探区断层瞬时相位时间切片来进行数据的匹配[9]。Nickel and Sonneland(2004)采用最小二乘法经过多次快速迭代实现自动同相轴匹配[10]。Xu和Stewart(2005)利用最大相关理论[11],在大套地层对准的原则上实现纵波和转换波的时间匹配。Fomel等(2005)利用最小二乘法,振幅和频率平衡匹配法,剩余γ0扫描法,和时间匹配微调的方法[12]来实现纵横波的匹配。Fomel和Jin(2009)介绍了一种基于两种数据局部相似性的方法进行时移地震数据匹配[13]。Wang等(2009)对比纵波和转换波的同层反射,辅以相似性最大原理求取γ0来实现数据匹配[14]。Bansal 等(2009)在纵波和转换波时间精确匹配的基础上,利用中、远偏移距地震道信息,拓展转换波由于动校正拉伸或固有因素导致衰减的高频信息[15],提高分辨率,从而实现二者频带的匹配。陈双全等(2010)利用纵横波速度比扫描方法校正数据偏差,并根据构造成像的标志性层位确定大致时间及速度范围选定计算时窗,进行速度比扫描得到最佳速度比算子,从而完成匹配[16]。Zhou等(2010)通过控制层位求取γ0值匹配苏里格地区的纵波和转换波剖面,并用全波测井数据进行匹配微调[17]。Chen等(2013)参考VTI介质各向异性特性,实现了转换波叠前双参数扫描结合纵横波速度比模型[18]的叠前匹配方法。然而,上述提出的方法大致都会有两大问题:(1)相关法中的相关时窗不能适应于变化剧烈的时移量,且计算效率、精度较低。(2)建立初始速度比模型本身就是一个难题,模型若偏差太大,迭代结果也不会理想。
面对上述问题,学者们转换思路进行了更深入的探索。Yuan等(2008)采用模拟退火算法求得纵波和转换波的最大相似性[19],实现二者的时间匹配。之后,Deng等(2011)开发出快速模拟退火算法[20]的相关应用。Hale(2013)实现了利用动态时间规整方法进行多维纵波与转换波数据的匹配[21],之后Hale和Compton(2013)改进该方法,利用误差累积进行时移量的平滑处理,完善了匹配效果[22]。Chen等(2014)利用叠前纵波反演得到的伪横波和转换波扫描估算速度比[23]实现匹配。Hyoungsu(2015)采用正则化全变差和分段线性基函数来构造时间规整最优函数[24],该方法能在厚层计算精确的速度比和避免时差的剧烈变化。Zhang(2017)凭借P波AVO反演出具有较高相关性的属性,然后利用DTW小范围匹配[25]。Wang(2017)提出范数拟合线性动态规整函数,再在稀疏性约束下匹配剖面[26]。在研究过程中发现,非线性最优化求解的思路在纵横波匹配中,相较于其他方法,有着更高的精度和效率,匹配结果更加理想。
本文正是在前人研究之上,为了提高匹配的精度和效率,利用具有非线性最优化特性的动态时间规整算法形成了基于数据驱动的纵波与转换波数据时间域匹配方法和实际数据处理技术流程。从经典的动态时间规整算法入手,改进完善了算法流程以适用于纵波与转换波数据的时间域匹配。在实际数据处理中,首先通过设定初始纵横波速度比,对纵波与转换波数据预匹配,使纵波与转换波的主要层位足够接近,满足应用动态时间规整算法的条件。然后,对转换波数据采用动态时间规整算法求取时移量,完成从转换波时间域匹配到纵波时间域的过程。最后,利用文中提出的纵波与转换波时间域匹配方法与数据处理流程,对一实际多波地震数据进行了纵波与转换波数据的匹配处理。
1 纵波与转换波时间域匹配原理
如图1所示,对于地下界面同一反射点的纵波与转换波数据,由于波传播的路径和传播的时间不同,观测到的同一反射点的地震波信息在纵波数据与转换波数据中,不仅时间不同,地震波的波形特征也会产生差异。
S表示激发的地震波的炮点,P为来自同一反射点C的纵波数据记录点,V为转换波记录点,O点为SP的中点位置,x表示观测的偏移距,h为反射界面的深度,VP与VS分别为地层的纵波与横波速度,α 为纵波入射角度与反射角度,β 为反射的转换波角度。
对于偏移或叠加处理后的叠加剖面,纵波与转换波数据中来自同一反射界面的反射波时间关系可以表示成:
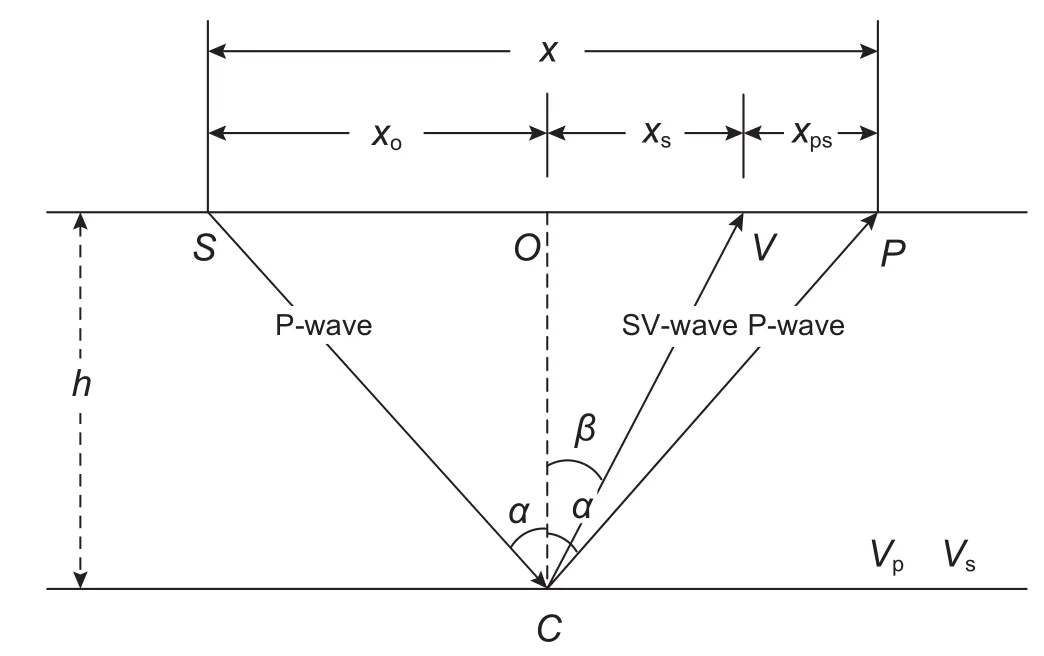
图1 纵波及转换波数据记录示意图Fig. 1 P-wave and converted-wave (C-wave) seismic data geometry chart
纵波的双程旅行时

和转换波的双程旅行时

设地层中的纵波与转换波速度比为γ=VP/VS,则有

因此,纵波与转换波数据在叠后剖面中进行的时间域匹配,就是根据公式(3)将转换波数据的旅行时间域转换到纵波旅行时间域。由于地震数据中地震了波的存在,使得这一匹配过程成为非线性反演问题,需要采用非线性方法进行处理。
2 动态时间规整算法
动态时间规整(Dynamic time warping,简称DTW)算法是在一定约束下,为两个信号序列寻找对齐的最优化路径的方法。该方法由Sakoe和Chiba(1978)提出[27],目前此算法在语音识别领域应用广泛[28],其中图2是最常见的时间序列信号匹配应用的例子。
而在地震数据处理中,Anderson和Gaby(1983)在地球物理的时间序列应用中基于动态时间规整算法提出了动态波形匹配算法[29],之后Liner和Clapp(2004)又提出了动态处理方法来解决地震记录各道之间的匹配问题[30]。
接下来,以两个合成地震记录f[ i],g[ i]为例,简单介绍DTW算法匹配时间域的地震信号的过程。假设两个地震记录在时间域内存在一个时差u[ i ],f[ i ]和g[ i ]的关系近似为

图2 两个时间序列信号的对齐Fig. 2 The alignment of two time series signals
在实际地震数据匹配问题中,f[ i ]和g[ i]是指数据中的采样点数值。DTW算法用于匹配纵波与转换波数据,需要完成以下三步处理得到时间域的偏移量。
2.1 对齐误差
纵波与转换波数据存在时移量,对齐误差则可以定义为:

式中,i是地震道上的某一个采样点数。l是记录在u[ i]中的时移量。这样就能建立一个横坐标是转换波数据的采样点数,纵坐标是时移量的对齐误差二维矩阵。
2.2 累积
累积就是对各个坐标点上的对齐误差依次迭代累积求和,得到累积误差d,公式如下:

由此得到各个坐标点上的累积误差。之后在累积误差的基础上回溯最优化路径,从而找到转换波数据地震道上每个采样点对应的时移量序列u[ i ]。
2.3 回溯
在完成累积处理后,需要遍历i=N−1上的所有l,
从而找到最小的d[ N−1,l],即

最小的d[ N −1,l ]中的l便是时移序列u[ i]的最后一个数值u[ N−1]。然后迭代寻找前一个时移量,直到最后找到第一个时移量u[0],公式如下:
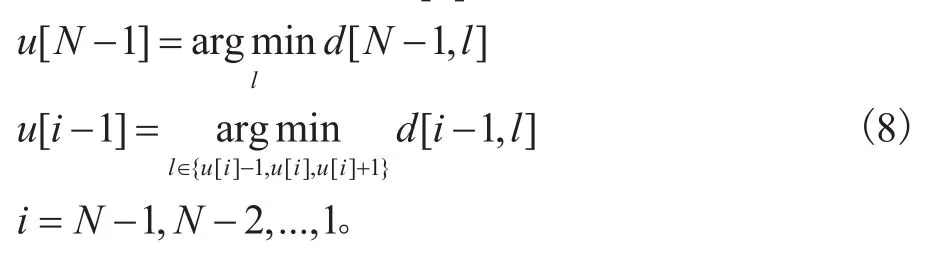
需要注意的是,为了防止相邻采样点之间的时移量变化太大,需要添加纵向约束条件:

以此保证各采样点的时移量纵向平滑变化。在此约束下,由后一个时移量迭代求前一个时移量时,就只需要在d[ i− 1,l−1],d[ i− 1,l],d[ i− 1,l+ 1]三者中比较找最小d,从而得到相应的时移量。最后,通过回溯最佳路径就找到了每一个采样点的时移量,依次记录在序列u[ i]中。
3 实际数据处理流程
本文基于动态时间规整算法,形成了纵波与转换波数据的时间域匹配方法。针对实际数据处理过程,建立了如图3所示的数据处理流程:
(1)按照层位控制纵波与转换波数据匹配的思路,通过设定初始纵横波速度比,根据公式(3)将转换波数据转换到纵波时间域,对转换波数据进行预匹配处理。
(2)tP表示纵波地震剖面的双程旅行时,tC表示相应的转换波地震剖面的双程旅行时,tP和tC之间的关系可以记为:

图3 实际数据处理流程图Fig. 3 Registration processing fl ow chart for real fi eld seismic data

u(tP)表示时移序列。利用预匹配处理后的转换波数据与纵波数据,采用动态时间规整算法求取纵波与转换波数据之间的时移量序列u(tP)。
(3)利用计算得到的时移量序列u(tP),对转换波数据进行更新匹配,之后,可以计算得到纵横波速度比模型。
(4)计算纵波数据与转换波数据之间的相关谱,验证最终的时间域匹配结果。
上述的(2)(3)步骤可以重复处理1~2次。
4 实际数据应用研究
在实际数据应用处理中,选用了一条二维陆上多波地震勘探数据中的纵波与转换波数据,进行该方法与处理流程的应用研究。该纵波与转换波地震剖面是经过常规数据处理后的叠后地震剖面,如图4所示,左图(图4a)为原始的纵波地震剖面,右图(图4b)为原始的转换波地震剖面。纵波数据的每道采样点数为1000,时间采样间隔为4 ms;转换波数据的每道采样点数为2000,采样间隔为2 ms,则原始的纵波与转换波数据的时间长度均为4 s。在匹配过程中,要将整个4 s时间长度的转换波资料匹配到纵波时间域。根据前面的实际数据匹配处理流程,该实际数据应用研究的过程主要包括以下三个方面。
4.1 转换波数据预匹配处理
由于地下介质的纵横波速度比一般介于1.5到3.5之间,因此我们可以先设定纵横波速度比γ为2,利用公式(3)建立起纵波和转换波时间域的射线传播双程旅行时的对应关系,将转换波转换到纵波时间域。由于相同地下介质中横波传播速度要小于纵波速度,转换波剖面的地质层位仅对应纵波剖面的一部分,因而选取了纵波时间3 s以内的数据进行匹配。另外,该数据的纵波与转换波的采样点数、采样间隔等参数存在一定的差异,因此在预处理中采用地震道内插值和重采样相结合的方法,使得二者的采样点数、采样间隔等参数统一。经过预处理,纵波和转换波剖面的采样点数和采样间隔分别相同,采样点数为2001,采样间隔为1 ms。用γ=2进行时间域预转换后的结果如图5所示,图5a为预处理后的纵波地震剖面,图5b为预处理后的转换波地震剖面。

图4 原始纵波剖面(a)和原始转换波剖面(b)Fig. 4 The original P-wave seismic section (a) and C-wave seismic section (b)
在图5中可以发现,转换波剖面经过最初设置的速度比γ=2的线性压缩后,图5a和图5b中从上到下的主要层位依次大致对应,在时间域上有较小的时移量偏差。所以,从预处理线性压缩后的结果中能够初步辨识出二者大致对应的地质层位。在预处理中,预先设定速度比并进行后续的线性压缩,其目的是为了大体上划定范围,将纵波与转换波剖面初步对应起来,以便之后应用动态时间规整方法时,避免大范围地扫描时移量而导致时移变化过大的情况发生。
4.2 应用DTW求取时移量进行时间域匹配
得到了预处理之后的纵波和转换波剖面后,就可以应用动态时间规整算法计算转换波剖面各道上的时移序列u[ i ]了。然后再利用时移序列对转换波剖面进行时间规整,实现转换波剖面精准匹配到纵波剖面时间域的结果。图6a展示的是将动态时间规整算法应用到预处理后的转换波剖面计算得到的各地震道的时移序列,在约束条件式(9)的限制下,纵向上每一道的时移量变化平缓。图6b是预处理资料中线性压缩掉的和DTW算法计算的时移量之和,即是原始数据的总时移量。
应用时移序列校正预处理后的转换波数据,得到规整后的转换波地震剖面(图7b)。图7对比了匹配后的转换波地震剖面和纵波地震剖面,图7a是纵波地震剖面,图7b是经过时移量规整到纵波时间域后的转换波地震剖面。对比图7a和图7b,可以看出规整后的转换波地震剖面完全刻画了PP波成像的主要构造。和纵波地震剖面层位整体一一对齐,二者主要的地质层位在时间域位置几乎完全相当,匹配结果一致性很好,精度较高,具有很好的可比性,完成了PS波传播时间到PP波传播时间的转化。
4.3 匹配结果分析
为了评估利用本文提出的方法和数据处理流程处理后的匹配效果,应用互相关法验证动态时间规整算法在转换波剖面与纵波剖面匹配中的实际效果。图8
是本文方法匹配前后的地震道数据的互相关时延谱。图8a是没有应用动态时间规整算法的纵波和转换波的互相关时延谱,图8b是动态时间规整算法校正后的转换波数据与纵波数据的互相关时延谱。

图5 预处理后的纵波剖面(a)和预处理后的转换波剖面(b)Fig. 5 The pre-processing P-wave seismic section (a) and the C-wave seismic section (b)
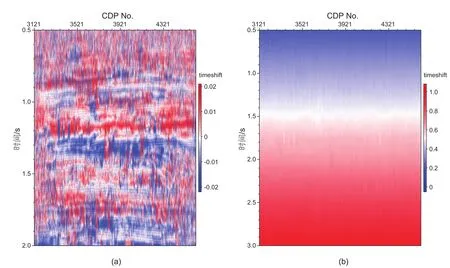
图6 由动态时间规整算法计算的预处理后资料的时移量(a)和原始数据的总时移量(b)Fig. 6 The time shifts (a) computed by using DTW method for pre-processing sections and the sum of the time shifts (b) for raw data

图7 (a)预处理后的纵波地震剖面和(b)用DTW算法计算的时移量匹配后的转换波地震剖面对比Fig. 7 Comparison of the (a) pre-processing P-wave seismic section and (b)time matching processed C-wave seismic section by using DTW method

图8 动态时间规整匹配前后的地震道数据的互相关时延谱比较.(a)应用动态时间规整匹配前的纵波与转换波数据的互相关时延谱;(b)应用动态时间规整匹配后的纵波与转换波数据的互相关时延谱Fig. 8 Comparison of correlation time shift spectrum computed by using the P- and C-wave seismic traces, (a) before using DTW method processing, (b) after using DTW method processing
图8a中较大的相关系数分散在各个时移量的位置上,说明动态时间规整算法前转换波剖面和纵波剖面没有达到匹配的效果,平均相关系数为-0.06,相关性极差。图8b中,在整个时间段上,最深的红色集中在零时延处,即零时延处几乎都达到较大的相关系数,整体相关系数大多分布在0.68左右,表明利用动态时间规整算法匹配后的转换波地震剖面与纵波剖面具有很好的一致性,匹配效果良好。其他时延位置较大的相关性的产生是由于地震子波的影响所致。比较动态规整时间域匹配前后的互相时延谱,可以定量确定,经过规整后的转换波地震剖面与纵波地震剖面的一致性得到极大的提升。
5 讨论与结论
本文利用非线性反演的DTW方法,直接从纵波与转换波数据之间的时移量入手,进行反演求取整个数据的时移量序列,完成了纵波与转换波数据的时间域匹配。经实际多波地震数据的应用,结果表明,文中提出的纵波与转换波数据时间域匹配方法和技术流程,可以很好地解决纵波与转换波数据匹配过程中的非线性问题,而且,匹配过程中不需要进行层位的控制或约束,就可以达到很好的匹配效果。众所周知,PP波与PS波的匹配是一个系统的复杂工程,不仅包括二者的运动学特征匹配,还包括动力学特征匹配与综合解释等。本文所展示的是如何在时间域完成匹配,解决二者的运动学非线性优化问题,还未考虑PP波与PS波的动力学特征匹配过程,这是本文下一步研究的方向。
本文取得如下几点认识:
(1)经典的动态时间规整算法需要做小小的改动引入时移量,便能够利用非线性全局最优化的思想找到纵波和转换波匹配的最佳路径。
(2)通过设定初始的纵横波速度比对纵波和转换波资料进行预处理,可以在整体上有效地找到二者对应的标志性层位,为之后应用动态时间规整算法更精细地依靠波形相似性计算时移量奠定基础。该方法的逐步精细化的研究思路具有很好的推广性。
(3)在计算转换波每一道的时移序列时,设定的时移量变化约束很好地限制了纵向时移量变化范围,使时移量在纵向上平滑变化。
(4)动态时间规整算法能够在纵横波匹配的应用中取得良好的效果。该方法跳出了以往利用人工层位拾取和利用纵横波速度比结合相关法或迭代法匹配的思路,避免了人为误差,相关窗口不适应时移量剧烈变化,计算效率较低和初始速度比模型难建立等一系列问题。转而利用非线性最优化的DTW算法计算的各个采样点的时移量直接校正转换波地震剖面,直观、便捷地实现了纵波与转换波数据匹配的目的。同时可以利用计算的时移序列推导出地层的纵横波速度比,为之后的地层速度建模提供了参考。
[1] LI X Y. Fracture detection using azimuthal variation of P-wave move out from orthogonal seismic survey lines[J]. Geophysics, 1999,64(4): 1193-1201.
[2] LI X Y, ZHANG Y G. Seismic reservoir characterization: How can multicomponent data help?[J]. Journal of Geophysics and Engineering, 2011, 8(2): 123-141.
[3] GAISER J E. Multicomponent VP/VScorrelation analysis[J]. Geophysics, 1996, 61(4): 1137-1149.
[4] CHAN W. Analyzing converted-wave seismic data: Statics, interpolation, imaging, and PP correlation[M]. Calgary: University of Calgary, 1998.
[5] VAN D R, GAISER J. Stratigraphic description of the Morrow formation using mode-converted shear waves: Interpretation tools and techniques for three land surveys[J]. The Leading Edge, 2001, 20(9): 1042-1047.
[6] GAROTTA R, GRANGER P Y, DARIU H. Combined interpretation of PP and PS data provides direct access to elastic rock properties[J]. The Leading Edge, 2002, 21(6): 532-535.
[7] FOMEL S, BACKUS M M. Multicomponent seismic data registration by least squares[C]. SEG Technical Program Expanded Abstracts,Dallas, 2003: 781-784.
[8] VAN D R, KRISTIANSEN P. Event registration and VP/VScorrelation analysis in 4C processing[C]. SEG Technical Program Expanded Abstracts, Dallas, 2003: 785-788.
[9] NAHM J W, DUHON M P. Interpretation and practical applications of 4C-3D seismic data, East Cameron gas fi elds, Gulf of Mexico[J].The Leading Edge, 2003, 22(4): 300-309.
[10] NICKEL M, SONNELAND L. Automated PS to PP event registration and estimation of a high-resolution Vp-VSratio volume[C]. SEG Technical Program Expanded Abstracts, Denver, 2004: 869-872.
[11] XU C, STEWART R R. Delineating a sand reservoir using inversion of 3C-3D seismic data[C]. SEG Technical Program Expanded Abstracts, Houston, 2005: 995-998.
[12] FOMEL S, BACKUS M, FOUAD K, et al. A multistep approach to multicomponent seismic image registration with application to a West Texas carbonate reservoir study[C]. SEG Technical Program Expanded Abstracts, Houston, 2005: 1018-1021.
[13] FOMEL S, JIN L. Time-lapse image registration using the local similarity attribute[J]. Geophysics, 2009, 74(2): A7-A11.
[14] WANG J S, HUO L, TIAN C C, et al. Lithology and fluid prediction using multiwave seismic data[C]. SEG Technical Program Expanded Abstracts, Houston, 2009: 1237-1241.
[15] BANSAL R, KHARE V, JENKINSON T, et al. Correction for NMO stretch and differential attenuation in converted-wave data: A key enabling technology for prestack joint inversion of PP and PS data[J]. The Leading Edge, 2009, 28(10): 1182-1190.
[16] 陈双全, 王尚旭, 李向阳, 等. 与 PP 波的时间匹配[J]. 石油地球物理勘探, 2010(4): 497-501. [CHEN S Q, WANG S X, LI X Y, et al. P-SV wave and PP wave time domain registration. Petroleum Geophysical Exploration, 2010(4): 497-501.]
[17] ZHOU Y J, TAO J Q, DOU Y S, et al. Quantitative interpretation and joint inversion of multicomponent seismic data: Application to the Sulige Gas Field, China[C]. SEG Technical Program Expanded Abstracts, Denver, 2010: 1646-1650.
[18] CHEN S Q, LI X M, LI X Y. Automated time-domain transform of converted waves by prestack double-parameter scanning[J]. Journal of Geophysics and Engineering, 2013, 10(4): 045010.
[19] YUAN J J, NATHAN G, CALVERT A, et al. Automated C-wave registration by simulated annealing[C]. SEG Technical Program Expanded Abstracts, Las Vegas, 2008: 1043-1047.
[20] DENG Z W, SEN M K, WANG U, et al. Prestack PP & PS wave joint stochastic inversion in the same PP time scale[C]. SEG Technical Program Expanded Abstracts, San Antonio, 2011: 1303-1307.
[21] HALE D. Dynamic warping of seismic images[J]. Geophysics, 2013, 78(2): S105-S115.
[22] HALE D, COMPTON S. Smooth dynamic warping[R]. CWP Reposts, 2013.
[23] CHEN S Q, LI X Y, TANG J. Converted-wave time domain registration using the inverted pseudo-PS-wave attribute section[J]. Journal of Geophysics and Engineering, 2014, 11(1): 015007.
[24] BAEK H, KEHO T H. Detection and characterization capabilities of time/amplitude warping[C]. SEG Technical Program Expanded Abstracts, New Orleans, 2015: 5379-5383.
[25] ZHANG T, SUN P, QIAN Z, et al. Automatic registration of PP and PS data based on seismic attributes[C]. 79th EAGE Conference and Exhibition, Paris, 2017.
[26] WANG H, SACCHI M, MA J. Linearized dynamic warping with l1-norm constraint for multi-component registration[J]. Journal of Applied Geophysics, 2017, 139: 170-176.
[27] SAKOE H, CHIBA S. Dynamic programming algorithm optimization for spoken word recognition[J]. IEEE transactions on acoustics,speech, and signal processing, 1978, 26(1): 43-49.
[28] MÜLLER M. Information retrieval for music and motion[M]. Heidelberg: Springer, 2007.
[29] ANDERSON K R, GABY J E. Dynamic waveform matching[J]. Information Sciences, 1983, 31(3): 221-242.
[30] LINER C L, CLAPP R G. Nonlinear pairwise alignment of seismic traces[J]. The Leading Edge, 2004, 23(11): 1146-1150.
