基于贝叶斯概率矩阵分解的地震数据重建算法
2018-07-03侯思安张峰李向阳
侯思安,张峰,李向阳
中国石油大学(北京)油气资源与工程国家重点实验室,北京 102249
0 引言
地震数据重建是提高资料品质和降低勘探综合成本的关键技术。经典的数据重建算法主要有预测滤波算法(Prediction Filter)和促稀疏反演算法(Sparsity Promoting Inversion):预测滤波算法是将含有缺失道的地震数据从时间—空间域变换到频率—空间域,然后根据数据在频率—空间域中表现出来的线性特征进行数据重建[1];而促稀疏反演算法是假设原始的地震信号在变换域中是稀疏的,当数据存在缺失时稀疏性会变弱,因此可以通过求解一个l1模规则化的最优化问题来恢复信号的稀疏特征实现数据重建[2-3]。这些算法的一个共同点是都依赖于解析数学变换如快速傅里叶变换(Fast Fourier Transform)[4],拉东变换(Radon Transform)[5],曲波变换(Curvelet Transform)[6]和地震小波变换(Seislet Transform)[7]等。但是受限于计算机的性能和实际地震资料的复杂性,解析数学变换已经很难满足石油工业对数据处理精度的需求。因此学术界将研究的重心转向了机器学习(Machine Learning)算法,希望能通过机器学习达到更好的数据重建效果。
就地震数据重建这个问题而言,主要的机器学习算法有稀疏字典学习算法(Sparsity Dictionary Learning)和低秩矩阵分解算法(Low-rank Matrix Factorization)。与数学变换算法相似,稀疏字典学习算法是通过输入数据自适应的生成一组变换基函数,在该基函数下原始的输入数据具有稀疏特征。目前计算精度最高的稀疏字典学习算法是k-SVD算法[8-9],在使用该算法进行地震数据插值时[10-11]:第一步,对原始数据进行Patch处理[12]并初始化一组基函数(在k-SVD算法中基函数被称为字典);第二步,求解l1模规则化问题计算稀疏系数;第三步,分别对基函数的每一列进行更新,更新每一列时要对残差矩阵进行一次SVD分解,并用分解的第一列左特征向量矩阵更新基函数,用右特征向量矩阵的第一行和第一个特征值的乘积更新系数矩阵的对应行;第四步,循环步骤二至步骤四若干次直至收敛为止。可以看出当基函数具有k列时,该算法每一次迭代都要进行k次SVD分解,巨大的计算量限制了该算法在实际资料处理中的应用。数据驱动的紧致框架(Data-Driven Tight Frame,DDTF)[13]则是一种改进的稀疏字典学习算法,该算法对基函数施加了紧致性约束条件,在每次迭代时仅需要一次SVD分解,极大地提高了数据处理的效率[14-15]。低秩矩阵分解算法则假设实际的地震信号具有低秩特征,但是当数据中存在缺失或噪音时,信号的秩会提高,因此可以设计一个降秩的优化算法实现地震数据重建[16],常用于地震数据处理的减秩算法有阻尼减秩算法(Damped Rank-reduction Method)[12],特征值收缩算法(Singular Value Shrinkage)[17]和多通道奇异谱分析算法(Multichannel Singular Spectrum Analysis, MSSA)[18]等。此外实际用于地震数据插值的都是4D或5D数据体,针对这种高维信号可以采用构建Hankel矩阵对数据降维[17]或直接应用张量分解算法进行求解[19-20]。
相比较而言低秩矩阵分解算法在求解最优化问题时不用处理l1模规则化,也不是必须要用SVD分解,因此在计算效率上具有一定的优势。但是在求解该算法时需要考虑多个最优化参数,多数情况下是通过设置不同的参数进行数据处理然后人工选取较优的结果,这样做会增大数据处理的计算量,且处理精度也难以保障。针对这一问题,Salakhutdinov和Mnih在求解推荐系统(Recommendation System)的矩阵分解问题时提出了贝叶斯概率矩阵分解(Bayesian Probabilistic Matrix Factorization,BPMF)算法[21],该算法可以对基函数和系数的均值和方差等统计学参数进行随机模拟,通过计算不同参数的概率密度函数自适应的选取最优结果,Net fl ix问题测试表明该方法具有良好的应用效果。本文将该算法引入到地震数据重建问题中,大量的数值测试表明该算法可以提高数据处理的精度和稳定性。本文首先介绍了地震数据矩阵分解的概率解释和BPMF算法的原理;然后,通过单道子波、合成地震记录和实际资料对该方法进行测试;最后,对算法进行总结和展望。
1 方法原理
1.1 基于概率矩阵分解的地震数据插值算法
基于概率矩阵分解(Probabilistic Matrix Factorization,PMF)[22]的地震数据插值算法通常假设实际地震信号矩阵是低秩的,并且可以表示为两个矩阵的乘积形式:

其中,X ∈ Rn×m表示含有随机缺失的地震数据,n和m分别表示矩阵的行数和列数;M ∈ Rn×k和 A ∈ Rk×m分别表示基函数和对应的系数,理论上k等于数据X的秩;E表示随机噪音矩阵。
由于基函数M和系数A都是未知的,很自然的假设的这两个矩阵的元素都是符合Gaussian分布的:

其中,N(y|ϕ, σ2)表示y符合均值为ϕ,方差为σ2的Gaussian分布;µi,j和ai,j分别表示M和A的元素;和分别表示M和A的方差;∏表示乘积运算符。
因为随机噪音E也是满足Gaussian分布的,所以:
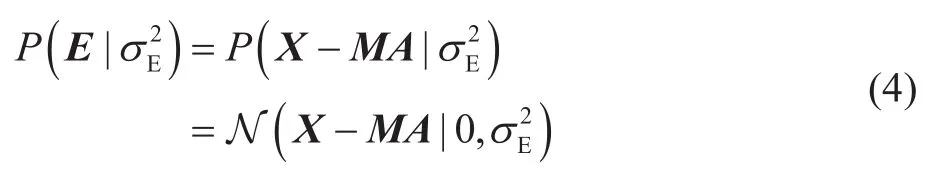
其中,σE2表示随机噪音E的方差。
根据概率密度函数的平移关系有:
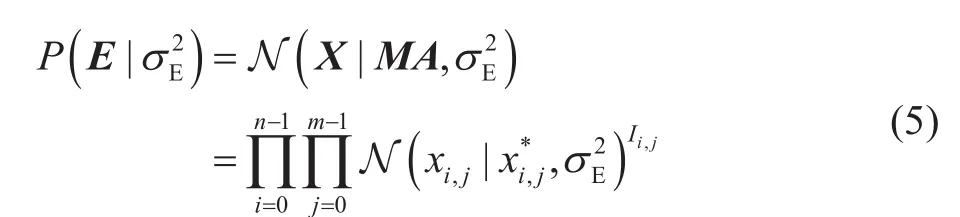
其中,表示重建地震数据X*= MA的元素;上标Ii,j用于标记数据的缺失信息,当该元素缺失时Ii,j=0,否则Ii,j=1。
因此基于PMF的地震数据重建等价于在采集数据X已知时,求取M和A的最大后验概率:
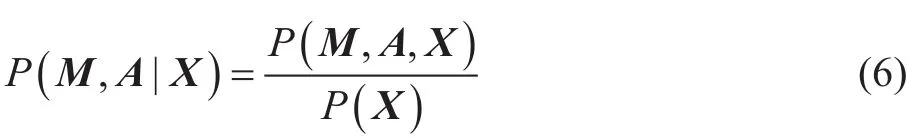
因为X是已知的,因此概率密度函数P(X)是一个常数,所以有:
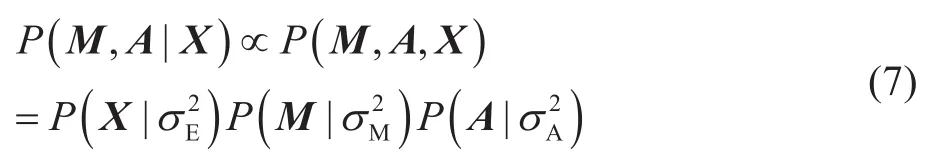
对公式(7)求对数并带入概率密度函数(2)、(3)、(5)和高斯分布函数,可以得到:
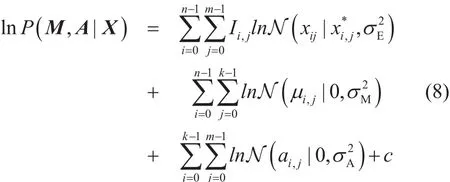
其中,c是用于平衡方程(8)左右两端的一个常数。
根据公式(8),在采集数据X已知时,求取基函数M和系数A的最大后验概率等价于求解如下的最优化问题:


图1 贝叶斯概率矩阵分解示意图Fig. 1 The graphical model for Bayesian Probabilistic Matrix Factorization
其中,xi,j和分别表示采集得到的地震数据和重建的地震数据;表示最优化权系数,和表示基函数M、系数A和随机噪音E的方差;表示l2模规则化;Ω表示采集数据的观测系统。
公式(9)描述了基于PMF的地震数据插值算法,在应用该算法进行数据重建时需要提前知道规则化参数λM和λA,而这两个参数又和基函数M、系数A和随机噪音E的方差和相关。其中随机噪音方差可以通过分析地震数据进行估算,但是和通常是无法获取的。一种普遍的做法是尝试用不同的参数进行数据处理,然后选取其中效果最好的作为最后的处理结果,但是这样做的计算量是比较大的。因此,本文将贝叶斯概率矩阵分解算法引入到地震数据插值问题中,基于该算法可以有效地解决规则化参数不确定的问题。
1.2 基于贝叶斯概率矩阵分解的地震数据插值算法
贝叶斯概率矩阵分解(Bayesian Probabilistic Matrix Factorization,BPMF)的核心原理是假设决定基函数M的系数A分布特征的超参数和是符合Gaussian-Wishart分布的,通过马尔科夫蒙托卡罗(Markov Chain Monte Carlo,MCMC)方法对不同参数的结果进行随机模拟,并计算不同参数对应的重建结果的概率密度函数自适应的选取最优结果。BPMF的示意图如图1所示。
根据前文的阐述,在BPMF算法中基函数M和系数A满足如下的高斯分布:


其中,Mi,:表示基函数矩阵M的第i行,A:,j表示系数矩阵A的第j列,和是决定基函数M和系数A分布特征的超参数,这两个超参数都符合Gaussian-Wishart分布:

其中,ξ0等于0,v0等于基函数的列数k,W0为大小是k×k的单位矩阵;W(Λ|W0,v0)表示Wishart分布:

其中,c表示归一化参数,Tr表示矩阵的迹。
在进行缺失地震数据重建时,可以利用贝叶斯边缘化处理(Marginalizing)来提高插值算法的精度。基本原理就是对任何可能出现的超参数{ΘM,ΘA}分别计算数据重建的结果,并对所有的结果进行加权求和,求和的权系数就是每个超参数对应的概率密度函数,因此基于BPMF的地震数据重建可以表示为如下的一个积分:
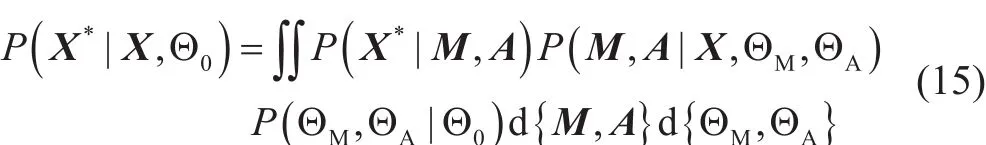
直接求解积分函数(15)几乎是不可能的,因此Salakhutdinov和Mnih提出了基于马尔科夫蒙托卡罗(Markov Chain Monte Carlo,MCMC)的求解方法。在MCMC的框架下,积分函数(15)可以近似如下的求和函数:

其中,表示马尔科夫随机采样序列,序列的长度是K。
本文使用Gibbs方法对公式(16)进行随机采样。由于地震数据插值仅需要概率最大的基函数M和系数A,所以实际计算时不需要完整的求解概率密度函数(16),而是通过多次迭代使得其达到稳定即可,那么基于BPMF的地震数据重建流程如下:
第一步,初始化基函数M(0)和系数A(0),初始化时可以采用其他算法求得的结果或直接采用随机函数生成得到,对输入地震数据进行Patch处理[12];
第 二 步, 更 新 超 参 数和由于基函数M和系数A在这一步中是已知的,超参数和的概率密度函数表示为:
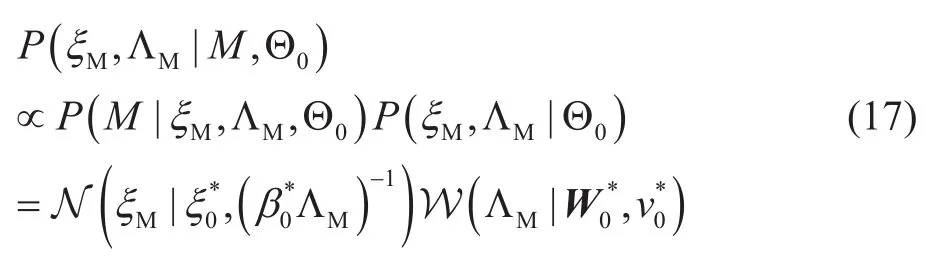
其中,

同理:
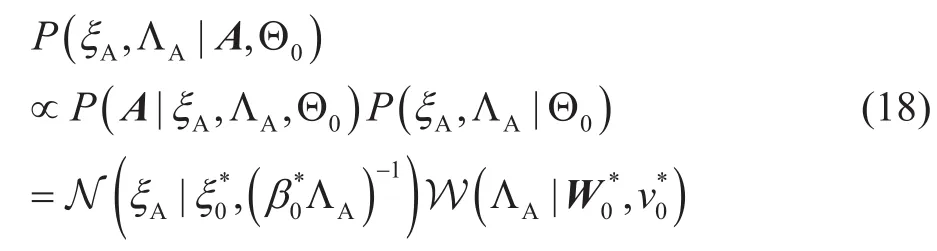
其中,


第三步,更新基函数M,根据贝叶斯公式:
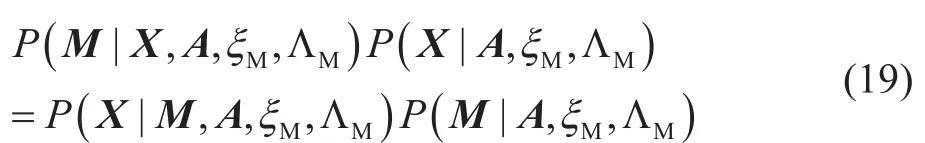
因为此时采集数据X,系数矩阵A和超参数都是已知的,所以条件概率密度函数P(X| A,ξM,ΛM)是一个常数,那么:

又因为基函数矩阵M和系数矩阵A是无关的:

所以:
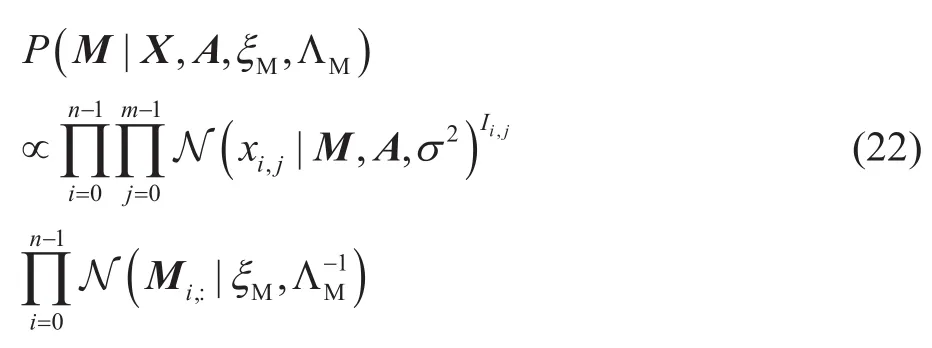
第四步,更新系数A,与第三步同理可以得:

最后,重复步骤二至步骤四直至基函数M和系数A达到稳定为止。
数据重建的流程如图2所示。
1.3 贝叶斯概率矩阵分解算法的稳定性分析
BPMF算法是一种随机缺失数据的恢复算法,要对缺失数据进行精确的恢复除了要求原始数据是低秩的,还要满足一定的采样条件。Candes和Recht对这一问题进行了深入研究,当随机采样满足如下的条件时即可用低秩算法进行数据重建[16],具体条件如下:

其中,e表示随机采样的数据点数;f =max(m, n)表示原始数据矩阵行数或列数的大值;r表示原始数据矩阵的秩;C表示一个数值常数。根据采样条件,当原始数据的秩r比较小时(Cf65r log f< m × n ),可以用随机采样的数据精确地恢复出原始数据;但是当r比较大时(Cf65r log f> m × n ),即便知道了所有有效信息,低秩算法也会造成原始数据的缺失。
图3表示用随机生成的低秩矩阵进行的BPMF方法稳定性测试。在测试中,原始数据矩阵是一个100× 100的方阵,矩阵的秩从1逐渐增加到41,采样率从0%逐渐增加到100%,数据重建的效果使用峰值信噪比(公式25)进行评估,并假设信噪比大于15时为重建成功,否则为失败。结果表明BPMF算法是一种精确稳定的低秩恢复算法,仅需要不到20%的随机采样数据就可以对低秩数据进行恢复。
基于BPMF的地震数据插值算法,在理论上可以有效的减少数据处理过程中对优化参数的依赖,提高数值计算的稳定性和精度,并用一个随机数矩阵验证了方法的稳定性。但是真正的地震数据并不是完全随机缺失的(表现为在时间方向连续缺失,在空间方向随机缺失),并且地震数据也不是完全低秩数据,这些问题可能会影响基于BPMF算法的地震数据重建效果。本文将通过合成地震数据和实际资料对本方法进行测试。
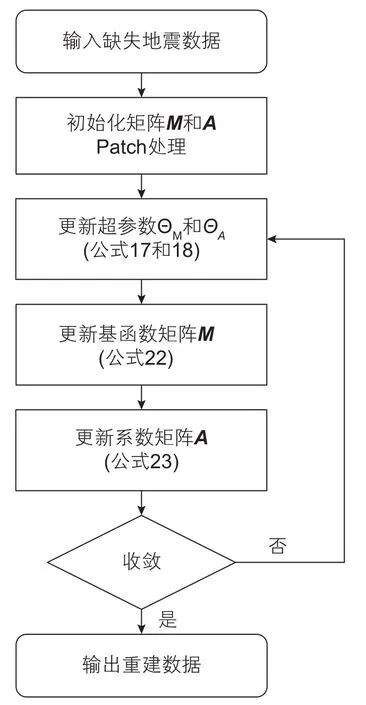
图2 贝叶斯概率矩阵分解算法计算流程Fig. 2 Workflow of Bayesian probabilistic matrix factorization algorithm

图3 随机数矩阵重建测试:白色表示重建成功;黑色表示重建失败Fig. 3 Illustration of random matrix recovery:white and black represents the successful recovery and failed recovery,respectively
2 方法测试
2.1 单道地震数据测试
首先通过随机缺失的单道地震子波数据对方法进行测试。单道记录如图4a所示,道集总共有401个采样点,采样间隔为1 ms,4个独立的子波主频分别为 15 Hz、30 Hz、15 Hz和 30 Hz,振幅分别为 1.0、1.0、3.0和3.0,数据总计有201道随机缺失。数据重构结果如图4b所示,4条不同的线段分别表示Patch大小为4、8、12和16的重构子波(Patch处理类似于地震数据的时窗概念,是一种常用的图像处理手段,具体定义可参考文献12),图4c和图4d分别表示了0~200 ms和 200~400 ms的局部放大图。根据Patch=4和Patch=8的重建结果,地震数据重建的Patch尺寸不能太小,否则会出现局部数据的采样不足,无法实现数据重建;同时对比Patch=12和Patch=16的重建结果,当Patch过大时,重建结果容易过度平滑;并且对比不同的子波结果发现,本文方法更容易使主频较高、振幅较强的数据产生平滑,因此在实际数据处理时需要尝试不同的Patch参数然后选取最优的计算结果。
2.2 合成地震记录测试
本文通过合成地震记录对提出方法进行测试。测试数据如图5a所示,原始数据具有201个地震道,每个地震道具有201个采样点,空间和时间采样步长分别为10 ms和7 ms,随机选取其中的40道为缺失数据,如图5b所示。在数据重建时选取基函数M的列数k等于20,规则化参数λM=λA=0.01。图5c、图5d和图5e分别表示基于Curvelet方法[23],PMF方法和BPMF方法的重建结果;图5f、图5g和图5h分别表示对应的重建数据残差。通过这一组数据对比表明,基于矩阵分解原理的PMF算法和BPMF算法比经典的Curvelet算法能更加有效地恢复地震数据,重建结果的残差明显减少。但是当数据在一定的区域内存在大量的缺失时,PMF算法的重建效果出现了较为严重的下降,如图5d的右侧所示。相比较而言,在相同的区域BPMF算法能较好的提高数据重建的效果,差剖面中没有明显的数据畸变,如图5h所示。

图4 单道地震记录测试:(a)含有随机缺失的单道数据,从左到右的子波依次为:主频15 Hz振幅1.0,主频30 Hz振幅1.0、主频15 Hz振幅3.0和主频30 Hz振幅3.0;(b)重建的单道数据;(c)0~200 ms局部放大图;(d)200~400 ms局部放大图Fig. 4 Single trace test:(a)Random missing single trace data, wavelets parameters(from left to right): 15 Hz amp=1.0, 30 Hz amp=1.0, 15 Hz amp=3.0 and 30 Hz amp=3.0; (b) Reconstructed single trace data; (c) Zoom of reconstructed data(0~200ms); (d)Zoom of reconstructed data(200~400 ms)
图6展示了基于BPMF算法进行地震数据矩阵分解得到的基函数M,其中图6a表示BPMF的基函数,图6b表示离散余弦变换(Discrete Cosine Transform,DCT)的基函数,每一个单独的数据块代表基函数的一列。可以看出BPMF算法的基函数的每一个数据块都非常类似于地震数据的同相轴,区别在于振幅和相位的不同。而DCT基函数是具有解析数学表达式的传统数学变换,每个数据块都是固定的,与输入数据无关。通过对比可以看出矩阵分解算法可以根据输入数据自适应的构建基函数M,具有特征提取的功能。

图5 合成地震记录测试:(a)原始数据;(b)含随机缺失数据;(c)Curvelet重建数据;(d)PMF重建数据;(e)BPMF重建数据;(f)Curvelet重建差剖面;(g)PMF重建差剖面;(h)BPMF重建差剖面Fig. 5 Synthetic data reconstruction test: (a) Original data; (d) Random missing data; (c) Reconstruction data via Curvelet; (d)Reconstruction data via PMF; (e) Reconstruction data via BPMF; (f) Residual of Curvelet reconstruction data; (g) Residual of PMF reconstruction data; (h) Residual of BPMF reconstruction data
为了更进一步的对比PMF算法和BPMF算法,测试了随机缺失道数从10道递增到100道,基函数M的列数k分别为15、20和25,以及规则化参数λM和λA分别为0.01、0.02和0.03的情况,测试结果如图7所示,峰值信噪比的计算公式为:

由于地震数据的复杂性以及信号噪音和缺失的干扰,这些重建参数是难以直接获取的,也没有一个明确的选取准则。但是通过这一组数据对比,当k从15逐渐增加到25并且规则化参数λM和λA从0.03逐渐减少到0.01时,PMF算法数据重建的精度在不断提高,但是也出现了较大幅度的波动,这说明算法的稳定性也有所降低,但是BPMF算法始终保持了一个较高的计算精度和稳定性。

图6 基函数示意图:(a)BPMF基函数示意图;(b)DCT基函数示意图Fig. 6 Illustration of basis matrix: (a) Basis matrix of BPMF; (b) Basis matrix of DCT

图7 PMF和BPMF对 比 测 试:(a)k =15测 试 结 果;(b)k =20测试结果;(c)k=25测试结果Fig. 7 Comparison PMF with BPMF: (a) Test result of k=15; (a) Test result of k =20; (a) Test result of k=25

图8 含噪音合成地震记录测试:(a)原始数据;(b)含随机缺失数据;(c)BPMF重建数据;(d)BPMF重建差剖面Fig. 8 Synthetic noisy data reconstruction test: (a) Original data; (b) Random missing data; (c) Reconstruction data via BPMF;(d) Residual of BPMF reconstruction data

图9 含噪音合成地震记录全部测试Fig. 9 Overview of synthetic noisy data reconstruction test
图8和图9则测试了在含有随机噪音的情况下,BPMF算法的重建效果,其中图8展示了随机25道缺失的重建效果,图9展示了随机缺失道数从10道递增到100道时的全部重建结果。通过这一组测试可以看出当数据中存在随机噪音时,BPMF算法依然可以稳定高效的对缺失地震数据进行重建。
2.3 实际地震记录测试
最后通过实际资料测试BPMF地震数据重建算法。测试使用的是海上OBC数据的一个剖面,该剖面有101个地震道,每个地震道具有2501个采样点,时间采样间隔为2 ms,截取其中1000 ms至3000 ms的一段数据用于测试,如图10a所示;测试时随机选取了其中的38道数据为缺失道,如图10b所示;基于BPMF算法的重建结果(k=25)和差剖面分别如图10c和图10d所示;图11则分别展示了第22道、第74道和第97道重建数据和原始数据的单道记录。通过对比重建的剖面和单道记录,大部分缺失的地震数据被精确的恢复出来了,特别是对于主频较低的深层信号,差剖面中几乎不含残留的有效信号,这说明本文提出的BPMF算法可以有效的对缺失地震数据进行重建。但是对能量较强的信号,数据恢复的结果中出现了比较明显的平滑,恢复信号的振幅能量降低了,这与单道记录测试结果是一致的,也是今后研究需要解决的问题。图12则展示了基于BPMF算法计算的基函数,该基函数依然体现出了非常明显的地震数据同相轴特征。
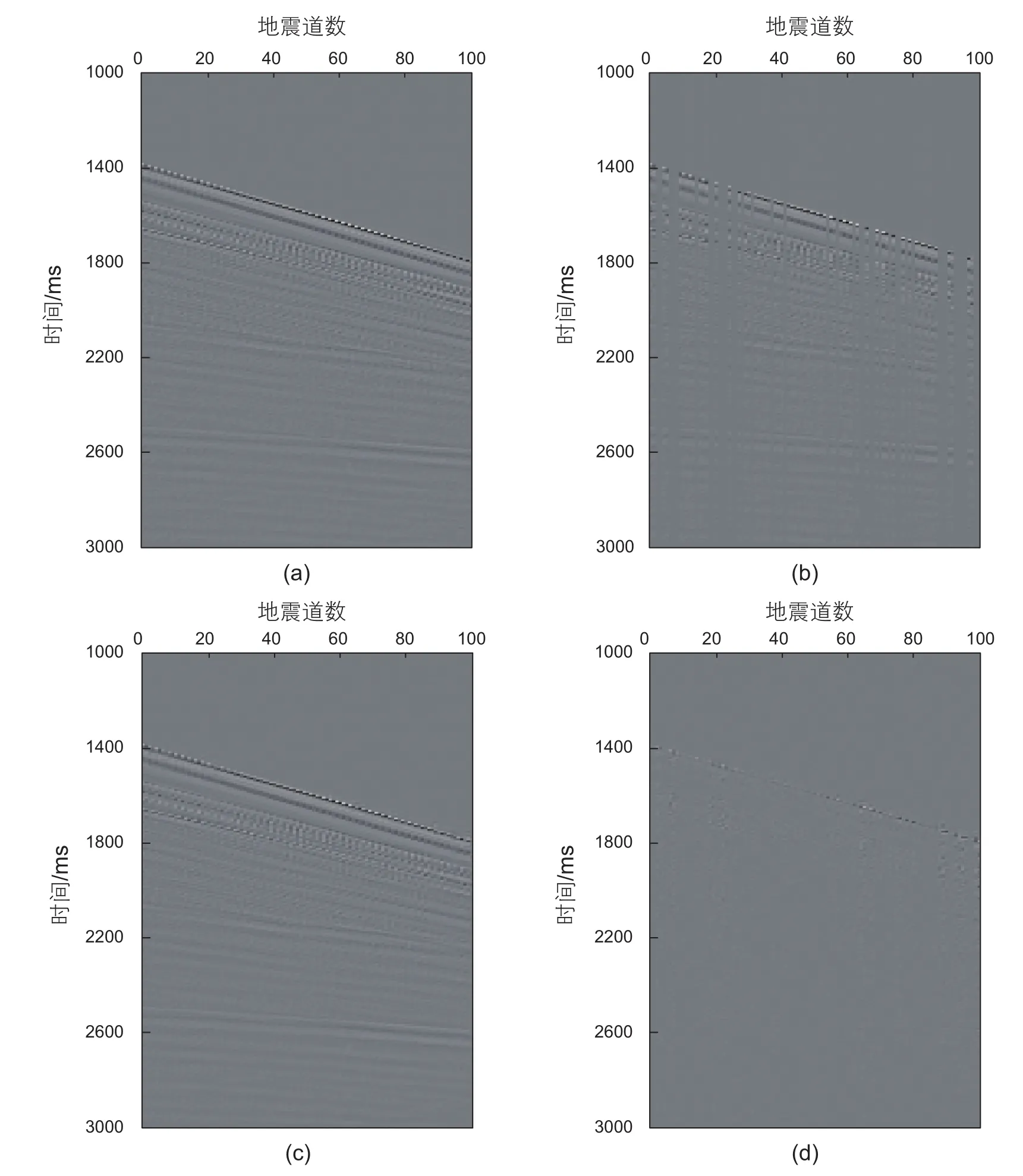
图10 实际地震数据测试:(a)原始地震数据;(b)含缺失道地震数据;(c)BPMF重建地震数据;(d)BPMF 重建差剖面Fig. 10 Real seismic data test: (a) Original seismic data; (b) Missing seismic data; (c) Reconstructed seismic data via BPMF;(d) Residual of BPMF reconstruction data

图11 实际地震数据测试单道记录:(a)第22道记录;(b)第74道记录;(c)第97道记录Fig. 11 Trace data of real seismic data test: (a) No. 22 trace data; (b) No. 74 trace data; (c) No. 97 trace data
3 结论与展望

图12 实际地震数据基函数Fig. 12 Basis matrix of real seismic data
矩阵分解算法是在地震数据信号处理中非常具有研究价值的工业应用前景的机器学习算法,在应用该算法时需要求解一个较为复杂的最优化问题,影响最终处理结果的有基函数M、系数A和随机噪音E的方差和以及基函数的列数k(理论上k应该等于实际地震数的秩)等参数。本文针对和的选取问题开展了研究,通过引入马尔科夫蒙托卡罗方法对不同的参数进行随机模拟并计算相应的概率密度函数自适应的选取最优结果,合成地震数据和实际资料测试表明该算法在计算精度和稳定性方面均有所提高。
但是该算法也存在一些需要研究和解决的问题。首先,当数据中能量较强的同相轴,本文算法会对结果产生一定的平滑作用,导致重建数据失真,初步分析认为这与Patch处理有直接关系,但是如何解决这个问题还需要深入研究;然后贝叶斯算法可以根据输入数据自适应的生成一个基函数,该基函数表现出了非常明显的地震数据特征,是否可以利用该基函数以及如何利用该基函数还是一个需要深入研究的问题。
[1] SPITZ S. Seismic trace interpolation in the F-X domain[J]. Geophysics, 1991, 56(6): 785-794.
[2] BAI L S, LIU Y K, LU H Y, et al. Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing[J]. Chinese Journal of Geophysics, 2014, 57(9): 2937-2945.
[3] HERRMANN F J, HENNENFENT G. Non-parametric seismic data recovery with curvelet frames[J]. Geophysical Journal of the Royal Astronomical Society, 2010, 173(1): 233-248.
[4] ABMA R, KABIR N. 3D interpolation of irregular data with a POCS algorithm[J]. Geophysics, 2006, 71(6): E91.
[5] WANG J, NG M, PERZ M. Seismic data interpolation by greedy local Radon transform[J]. Geophysics, 2010, 75(6): WB225-WB234.
[6] CANDÈS E, DEMANET L, DONOHO D, et al. Fast discrete curvelet transforms[J]. multiscale modeling & simulation, 2006, 5(3):861-899.
[7] FOMEL S, LIU Y. Seislet transform and Seislet frame[J]. Geophysics, 2010, 75(3): V25-V38.
[8] AHARON M, ELAD M, BRUCKSTEIN A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation[J].IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322.
[9] ELAD M, AHARON M. Image denoising via sparse and redundant representations over learned dictionaries[J]. IEEE Transactions on Image Processing, 2006, 15(12): 3736-3745.
[10] BECKOUCHE S, MA J. Simultaneous dictionary learning and denoising for seismic data[J]. Geophysics, 2014, 79(3): A27-A31.
[11] CHEN Y. Fast dictionary learning for noise attenuation of multidimensional seismic data[J]. Geophysical Journal International, 2017,209(1): 21-31.
[12] MA J. Three-dimensional irregular seismic data reconstruction via low-rank matrix completion[J]. Geophysics, 2013, 78(5):V181-V192.
[13] CAI J F, JI H, SHEN Z, et al. Data-driven tight frame construction and image denoising[J]. Applied & Computational Harmonic Analysis, 2014, 37(1): 89-105.
[14] LIANG J, MA J, ZHANG X. Seismic data restoration via data-driven tight frame[J]. Geophysics, 2014, 79(3): V65-V74.
[15] YU S, MA J, ZHANG X, et al. Interpolation and denoising of high-dimensional seismic data by learning a tight frame[J]. Geophysics,2015, 80(5): V119-V132.
[16] CANDÈS E J, RECHT B. Exact matrix completion via convex optimization[J]. Foundations of Computational Mathematics, 2008, 9(6):717.
[17] CHEN K, SACCHI M D. Robust reduced-rank fi ltering for erratic seismic noise attenuation[J]. Geophysics, 2015, 80(1): V1-V11.
[18] CHEN Y, ZHANG D, JIN Z, et al. Simultaneous denoising and reconstruction of 5-D seismic data via damped rank-reduction method[J].Geophysical Journal International, 2016, 206(3): 1695–1717.
[19] KREIMER N, SACCHI M D. A tensor higher-order singular value decomposition for prestack seismic data noise reduction and interpolation[J]. Geophysics, 2012, 77(3): V113-V122.
[20] GAO J, STANTON A, SACCHI M D. Parallel matrix factorization algorithm and its application to 5D seismic reconstruction and denoising[J]. Geophysics, 2015, 80(6): V173-V187.
[21] SALAKHUTDINOV R, MNIH A. Bayesian probabilistic matrix factorization using Markov chain Monte Carlo[C]. International Conference on Machine Learning, Helsinki, Fabianinkatu, ACM, 2008: 880-887.
[22] SALAKHUTDINOV R, MNIH A. Probabilistic matrix factorization[C]. International Conference on Neural Information Processing Systems. Vancouver, Canada, 2007: 1257-1264.
[23] DAUBECHIES I, DEFRISE M, DE MOL C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Communications on Pure & Applied Mathematics, 2004, 57(11): 1413-1457.
