新型旋转型行波超声波电动机定子的研究

郎梦梦,曾劲松 ,张西平

(郑州大学，郑州 450001)

0 引 言

超声波电动机(USM)是一种全新概念的直接驱动装置，属于新型微特电机中较为成熟的一种。不同于传统的电磁原理电机，超声波电动机是利用转子与定子之间的摩擦耦合驱动而形成的一类电机。超声波电动机依据波的传播方式可以分为行波型超声波电动机和驻波型超声波电动机。旋转型行波超声波电动机是行波超声波电动机中最具代表的一种，它利用压电材料的逆压电效应，将电能转换成机械能，从而驱动转子转动[1]。该电机具有低速大转矩、无电磁干扰、结构紧凑、运行无噪声、动作响应快、断电自锁等显著特征，具有传统电磁式电机难以替代的作用，在精密驱动领域显示了广阔的应用前景[2,3]。

超声波电动机作为高度精密的机电产品，其输出性能很大程度上依赖于加工精度。然而现有的定子在材料方面，大都采用铜材料；在结构工艺方面，定子齿采用在平面上铣削开槽方式形成，由于定子齿与齿之间间距小，属于窄槽加工，结构复杂，使得加工难度大，加工成本高，精度低。加工精度影响加工尺寸，从而影响电机的机械性能。本文对现有的一种旋转型行波超声波电动机定子进行研究，此定子相对于传统超声波电动机有较大的改进：材料方面，采用钢；结构方面，采用矩形发射齿形状和冲压加工工艺，具有结构简单，高精度加工容易控制，驱动力矩大，成本低等特点。因此，研究新型超声波电动机定子的结构对于设计开发有重要的借鉴意义。

1 旋转型行波超声波电动机原理

本文的电机采用面外振动模式，运用直接激励的方式使定子形成行波，在压电陶瓷组件上施加相位差为π/2的2个同频(超声频段)且等幅的A相电压与B相电压。利用压电陶瓷材料的逆压电效应，可在定子的模态频率上激发出2个幅值相等、在时间和空间上均相差π/2的A相驻波与B相驻波。这两相驻波在定子上叠加形成向前进的行波，在定子驱动端各质点的作用下，通过摩擦驱动转子向行波行进方向的反方向转动。

A相电压与B相电压在压电陶瓷片上激励的模态阵型可以表示:

ZA=IAsin(nθ)cos(wnt)

(1)

ZB=IBcos(nθ)cos(wnt+φ)

(2)

式中：IA，IB为两相激励响应的幅值；φ为两相响应的相位差。

依据模态阵型线性叠加原理，定子的位移响应:

当φ=π/2，IA=IB=I0时,得到行波:

Z=I0sin(nθ-ωnt)

(4)

因此，在压电陶瓷片组件上施加相位差为π/2的2个同频率、等幅值的交变电压，就可以产生行波。图1为行波形成示意图。

图1 行波形成示意图

2 超声波电动机定子结构分析

超声波电动机定子结构如图2所示，由内支撑板、齿结构、基体、压电陶瓷4部分组成。定子齿中间为环形，周向为矩形齿，多条矩形齿沿环形圆周边缘延伸的方式呈均匀辐射状分布。齿周向上翘起作为与动子接触部分，齿周上翘增加了定子质点的轴向位移，从而增大了电机的输出转矩。齿与齿之间开槽提高转子的驱动效果[4]。定子齿下表面粘接与之外径相同的钢制环状基体，便于压电陶瓷的粘接，压电陶瓷片粘接在基体下表面。

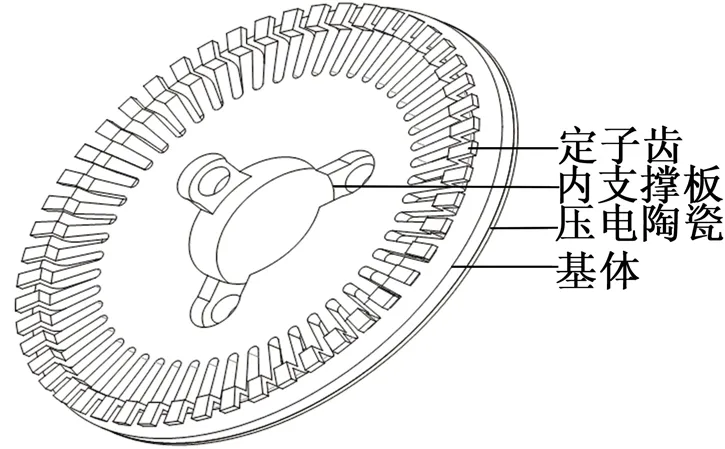
图2 定子结构图

在定子结构中，每个齿占据齿高H,定子齿内圆周距孔周距离L,齿与齿之间开槽角度S，以及弹性基体厚度W，是影响定子机械性能的主要参数，因此研究这些参数对了解电机的机械性能具有重要的意义。其中定子齿直径D=60 mm,每个齿占据圆周3.6°，压电陶瓷厚度0.5 mm为定值。图3标注了重要的结构尺寸参数。

图3 定子结构参数图

3 超声波电动机定子动力学分析

旋转型行波超声波电动机具有十分典型的运动机理,它深刻揭示了驻波和行波之间的转化关系以及能量转换与传递过程,并且其动力学模型对探究如何提高电机的多项性能指标有重要的实际意义。通过对超声波电动机进行实体建模以及动力学分析,可以明确超声波电动机的输出特性,评价其性能的优劣,探究各种因素对电机运转性能的影响程度。

通过ANSYS有限元分析软件进行建模，对定子进行模态分析，可模拟超声波电动机定子的实际振动，从而获得定量化的分析结果[5]。因电机环形的宽度相对于电机直径较小，所以通常用无节圆的B0n模式[6]。此定子选用B09工作模态，分析不同结构尺寸对模态频率的影响。

谐响应分析是用于分析持续周期变化的载荷在线性结构系统中所产生的稳态周期响应。对定子进行谐响应分析，可以确定定子振动模态在相应振动频率范围内所产生的最大振幅，定子振幅越大，定子行波表面质点的切向速度越大，从而使转子的转速变大，以此来提高电机的输出性能[7]。对不同齿高定子进行谐响应分析，为了便于提取定子波峰处振幅，施加峰峰值为160 V的单向正弦电压。因定子周向Y与轴向Z的位移构成了定子质点的椭球运动，所以需提取定子齿上相同径向距离质点的周向Y和轴向Z位移。

初始设定定子直径D=60 mm,L=12 mm，W=1.5 mm,S=3.6°，通过改变齿高H，得到的结果表1所示。

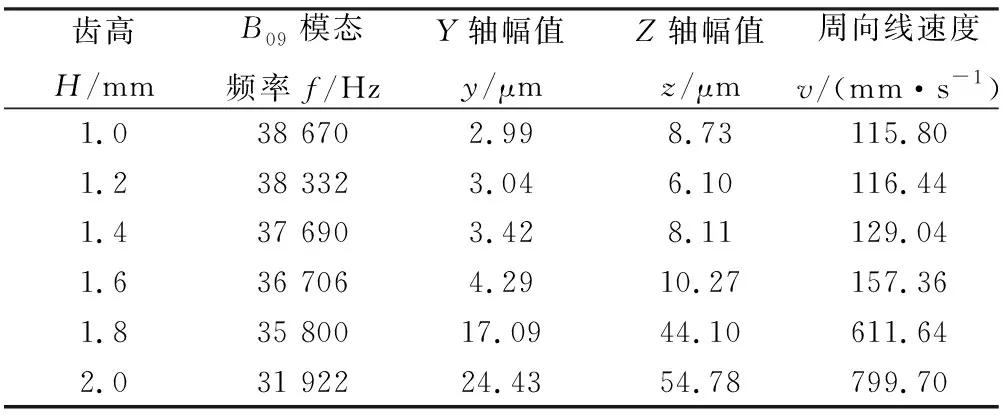
表1 改变齿高H分析结果

由表1可知，随着齿高由1mm增加到2mm，定子振动模态频率整体呈降低趋势，定子轴向和周向位移整体呈增加趋势。在齿高由1.6mm增加到1.8mm时，定子周向线速度有一个跳跃性的增加，且定子周向线速度与齿高成正比，所以齿高增加可以提高电机的空载转速。

设定定子直径D=60mm，L=12mm，W=1.5mm，H=1.4mm，通过改变定子齿与齿之间开槽角度S,即改变齿数，对定子进行模态分析与谐响应分析，结果如表2所示。

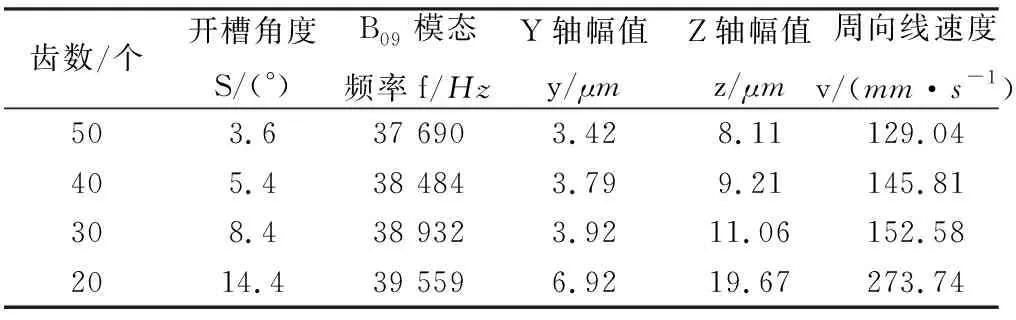
表2 改变开槽角度S分析结果

由表2可知，随着齿与齿之间开槽角度S的增加，即齿数的减少，定子模态频率呈增加趋势，周向位移与轴向位移逐渐增加，周向线速度逐渐增加。但是随着齿数的减少，定子与转子的接触部位减少，这将不利于电机的稳定运转，所以在设计定子的齿数时，应该综合考虑各方面的影响。

设定定子直径D=60mm,H=1.4mm,W=1.5mm,S=3.6°，改变定子齿内圆周距孔周距离L，对定子进行模态分析与谐响应分析，结果如表3所示。

表3 改变距离L分析结果

由表3可知，随着距离L的减小，定子模态频率逐渐降低，周向位移、轴向位移以及周向线速度整体呈降低趋势。

设定定子直径D=60 mm,H=1.4 mm,S=3.6°，L=12 mm，改变弹性基体厚度W,对定子进行模态分析与谐响应分析，结果如表4所示。

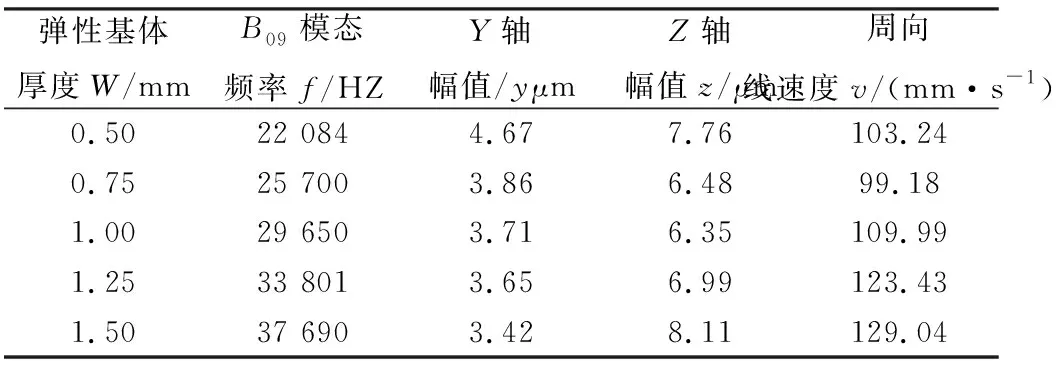
表4 改变基体厚度W分析结果

由表4可知，弹性基体对模态频率有较大的影响，随着基体厚度的增加，相同模态的频率值增加显著。这是由于随着基体厚度的增加，定子的刚度增大，所以相同模态对应的频率显著提高。随着弹性基体厚度的增加，轴向与周向位移呈下降趋势，周向线速度呈上升趋势。

4 超声波电动机定子整体性能分析

设定定子直径D=60 mm,齿高H=1.4 mm，齿数为50，即齿之间开槽角度S=3.6°，定子齿内圆周距孔周距离L=12 mm，基体厚度W=1.5 mm时，对定子进行性能分析。

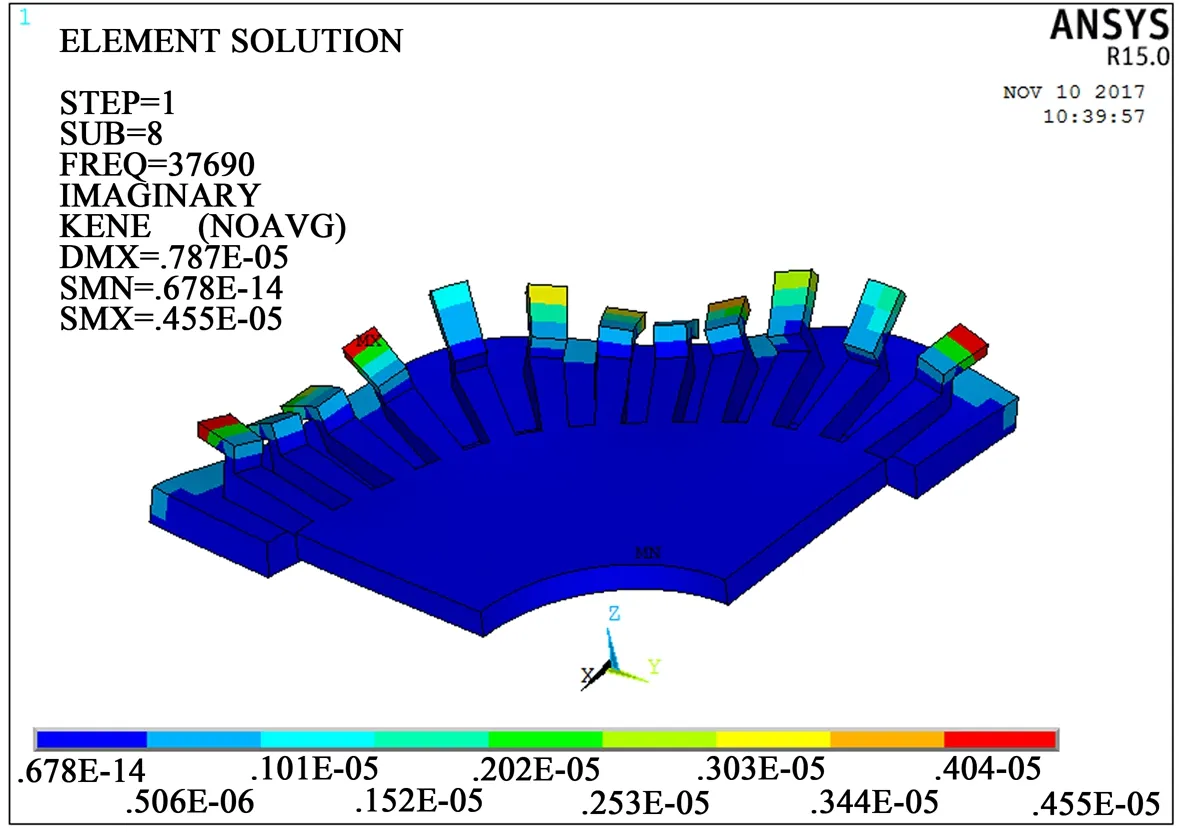
图4 整体能量图

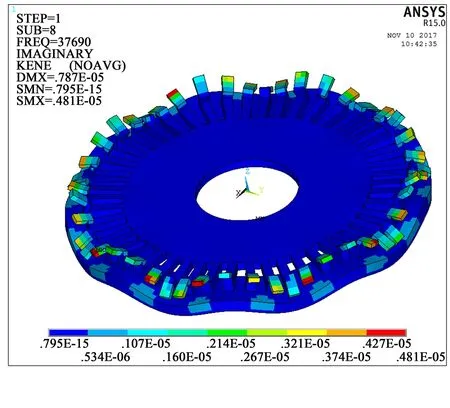
图5 局部能量图

图4、图5为定子B09振型时的能量图。由图4、图5可知，能量集中在与转子直接接触的齿周上，中间部分能量几乎为零，这种结构设计使得能量充分利用，不造成能量的浪费。

位移振型图如图6所示。定子齿周位移最大，中间部分位移较小，这种设计提高了与转子接触部分定子的周向位移和轴向位移，提高了振动幅度，从而提高电机旋转速度，也再次验证了定子设计的优越性。

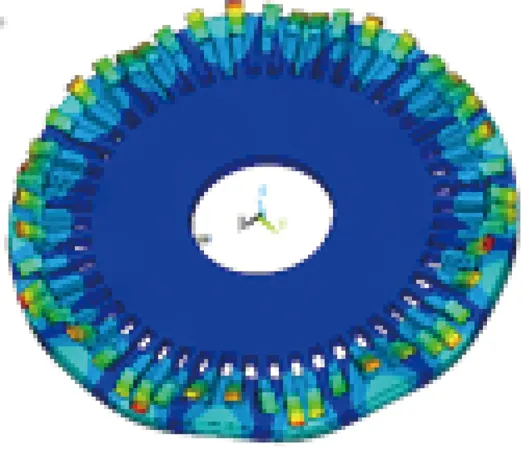
(a)A相振型

(b)B相振型

5 定子样机性能分析

因电机存在材料均匀性误差、实际加工误差、安装配合误差等，导致有限元分析软件的理论分析结果与实际测试结果存在偏差。为了更好实现对电机的控制，采用实验对样机机械性能进行分析必不可少。

本文分别对新型超声波电动机样机和传统超声波电动机施加峰峰值为400 V的电压，频率为B09振动频率，预压力为120 N，进行实验，结果如图7所示。

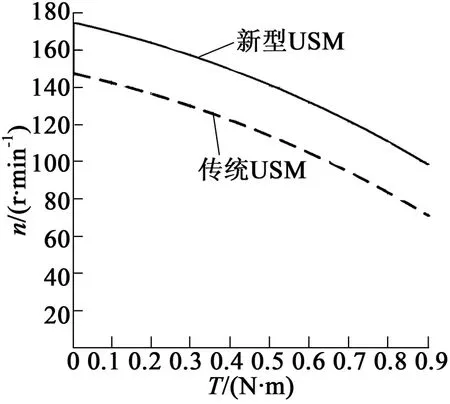
图7 负载特性图

实验表明，新型旋转型行波超声波电动机相对于传统USM在整体机械性能方面有较大提升，与有限元分析结果一致。

6 结 语

定子的振动特性对于超声波电动机的输出性能至关重要，通过有限元分析软件对现有的一种新型超声波电动机进行结构分析，通过改变结构的尺寸，研究不同定子尺寸对电机动态特性的影响，包括对模态频率结果与谐响应结果的影响。最后对于确定尺寸的定子进行整体性能分析，通过提取能量分布图与位移振型图，验证该定子设计的合理性与优越性，对于今后设计新型超声波电动机具有借鉴意义。

[1] 赵淳生.超声电机技术与应用[M].北京:科学出版社，2007．

[2] HAGOOD N W IV,MCFARLAND A J.Modeling of a piezoelectric rotary ultrasonic motor[J].IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control,1995,42(2):210-224.

[3] SASHIDA T,KENJO T.An introduction to ultrasonic motors[M].Oxford:Clarendon Press,1993.

[4] 陈如娟，陈超，宋小刚.微小旋转型超声电机瞬态特性测试及机械特性估计方法[J].机械工程，2011,22(11):1284-1288.

[5] 曾亮，沈萌红，钱孝华.ANSYS在超声波电机设计中的应用[J].机电工程，2009(3)：84-86.

[6] 莫岳平,胡敏强.超声波电机振动模态有限元分析[J].中国电机工程学报，2002，22(11)：92-96.

[7] 陈超，曾劲松，朱华.微型行波超声电机定子的参数优化设计[J].中国机械工程，2009，20(5)：568-572.