基于电流观测器的PMSM反推终端滑模控制

徐小明,赵清江

(新乡职业技术学院，新乡 453006)

0 引 言

永磁同步电机(以下简称PMSM)具有结构简单、效率高、转动惯量较小、过载能力强等优势,现如今已被大量运用于新能源汽车、高速铁路、机器人等许多工程领域。常规的PID调节方式已经不能达到高性能的控制需求，于是，对于交流永磁同步电机控制方法的研究具有重要的现实意义[1]。

传统的PMSM控制系统往往需要至少两相交流电流传感器来检测电流信号，这种获取电流的方式会额外增加电机的设计成本及电机本体体积，当其中一个电流传感器产生故障或失效时，所获取的电流信息将会带来系统控制的误差。这将严重影响PMSM 在精度和可靠性要求较高的场合中的应用。文献[2-4]中已经探索了利用单个电流传感器获取和重构相电流信息的技术。因此，本文考虑仅在单相电流传感器可用的情况下，设计了基于单相电流传感器的PMSM调速系统。

文献[5]提出了一种采用空间矢量调制控制技术(以下简称SVPWM)的三相直接矩阵变换器(以下简称DMC)驱动系统中，单电流传感器交流电机电流重构的方法。该算法将零矢量应用时间分为2个区间，并利用单霍尔电流传感器在DMC中来测量相电流。通过对三相异步电动机的仿真，验证了该系统的有效性。但是该方法对电力电子元件的性能提出了考验。

文献[6]针对三相电压型逆变器PMSM调速系统，提出了一种简单的单电流重构方法，研究了一种具有开关状态调整方案的空间矢量脉宽调制技术。该方法采用单电流传感器和嵌入式微系统构成三相永磁同步电动机驱动系统，完成了硬件实现，未对控速系统的动静态性能进行研究。本文将在单电流传感器系统的基础上，进一步分析与研究控制系统的动态性能和鲁棒性。

本文研究了一种基于单电流传感器的PMSM反推终端滑模控制。针对只有一相电流传感器的PMSM控制系统，设计自适应观测器实现对另外两相电流和时变定子电阻的准确估计。将反推控制与终端滑模控制进行结合，研究了一种基于终端滑模负载观测器的反推控制方法，有效地提高系统的收敛速度，增强系统的鲁棒性。利用李雅普诺夫理论证明了系统的稳定性。仿真及实验结果验证了该方法的有效性。

1 PMSM数学模型

以表贴式PMSM为控制对象，假定永磁体无阻尼作用且空间磁场分布为正弦分布，不计涡流与磁滞的损耗的情况下，PMSM在d，q坐标系和α，β坐标系下的动态数学模型[7-10]:

(1)

(2)

PMSM机械运动方程：

(3)

电磁转矩方程:

(4)

式中：ud,uq分别为d,q轴的电压分量；id,iq分别为d,q轴的电流分量；uα,uβ分别为α,β轴的电压分量；iα,iβ分别为α,β轴的电流分量；L为定子电感；R为电机定子绕组的电阻；ω为电机的电角速度；ψf为永磁体与定子交链磁链；Te为电磁转矩；J为转动惯量；TL为负载转矩；B为粘滞系数；p为极对数。

2 自适应电流观测器设计

假设在PMSM调速系统中，可用的电流传感器为b相时，根据式(2)α，β坐标系下电流方程，经过Clarke变换可得:

(5)

对式(5)求导可得:

(6)

将式(2)代入式(6)可得:

(7)

设计b相自适应电流观测器：

(8)

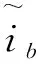
定义误差变量：

(9)

将式(8)和式(7)作差，可得:

(10)

设计定子电阻自适应律，构造Lyapunov函数：

(11)

式中:r>0。

将(11)求导可得：

(12)

假设式(13)成立：

(13)

这样，式(12)可改写：

(14)

由于，在自适应观测器的采样时间内，定子电阻的变化基本可以忽略，所以有：

(15)

这样可以得出：

(16)

因此，由式(13)可得自适应定子电阻方程式：

(17)

因此，定子电阻的估计值就可以有效地趋近于实际值。

为了提高定子电阻的估计精度，确保零稳态误差,采用PI控制策略进行如下调整：

(18)

式中:Kp，KI分别为比例积分常数。

将定子电阻估计值代入式(2)，则自适应观测器的最终表达式：

(19)

结合式(7)、式(18)和式(19)可以得到设计的自适应观测器。

3 反推终端滑模控制器的设计

为了提高系统的动态性能，结合反推控制与终端滑模控制各自的优势，设计基于终端滑模负载观测器的反推终端滑模控制器[11-14]。

由式(3)、式(4)可得:

(20)

可以得到转矩观测器的状态空间表达式:

(21)

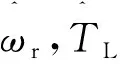
(22)

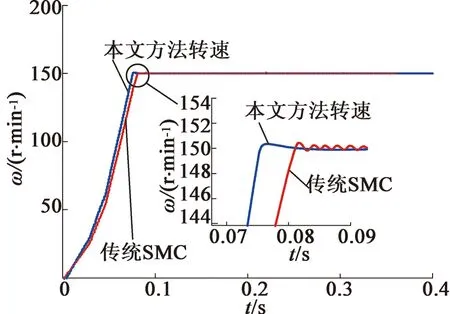
式中：β>0,1

为有效地抑制滑模存在的抖振现象，保证非奇异性，采用一种带终端吸收引子的趋近方式设计趋近律：

(23)

式中：φ1<0,φ2<0,0<γ<1。

(24)

(25)

构造Lyapunov函数：

(26)

将其微分可得：

(27)

(28)

式中：r2>0。

结合式(28)和式(27)，则：

(29)

定义电流的跟踪误差：

(30)

其微分方程：

(31)

选取式(22)为滑模面，设计反推终端滑模速度控制器:

构造PMSM调速系统的Lyapunov函数：

(33)

将式(33)微分可得：

(34)

结合式(30)、式(31)可得：

(36)

式中：rd>0,rq>0。

4 仿真及实验验证

为了检验本文的控制策略的有效性，通过MATLAB/Simulink搭建了系统仿真模型，控制系统仿真及实验电机的主要参数如表1所示，PMSM调速系统的控制框图如图1所示。

表1 PMSM驱动系统的主要参数

图1 PMSM调速系统的控制框图

图2为本文算法与传统PI滑模控制对比的转速空载响应曲线。系统初始给定转速为150 r/min，从图2可看出,采用本文算法的PMSM调速系统，起动平稳无超调，到达稳态的时间更短。

图2 空载响应曲线

图3为系统受到负载扰动时2种控制方法对比曲线。系统在0.2 s时加载2 N·m，在0.3 s时卸载。从图中可明显看出，本文控制方法在加载时鲁棒性更强。

图3 扰动时转速响应曲线

为了进一步验证本文算法的正确性，搭建PMSM矢量控制系统实验平台，实验是建立在TMS320F2812实时控制系统中进行，实验结果达到预期效果。

图4是实测的转子位置曲线。说明本文所采用的估控制方法控制精度高，控制系统性能较好。

图4 实测转子位置

图5为电机空载起动时稳定状态对应b相电流波形。从图5可看出，在电机达到稳定运行状态时，定子电流稳定且正弦度较好。电机转速能够在有限时间内平稳到达给定转速。

图5 升速时转速和相电流波形

5 结 语

本文在单电流传感器的PMSM调速系统基础上，设计自适应观测器实现对另外两相电流和时变定子电阻的准确估计。将反推控制与终端滑模控制进行结合，研究了一种基于终端滑模负载观测器的反推控制方法。仿真及实验结果验证了本文的控制策略能够有效地提高系统的收敛速度，增强系统的鲁棒性。

[1] 邵伟,李晓宁,董明.永磁同步电机伺服系统控制策略综述[J].电气自动化,2013,35(1):1-3，16.

[2] GREEN T C,WILLIAMS B W.Derivation of motor line-current waveforms from the DC-link current of an inverter[J].IEE Proceedings B-Electric Power Applications, 1989,136(4):196-204.

[3] BLAABJERG F,PEDERSEN J K.An ideal PWM-VSl inverter using only one current sensor in the DC-link[C]//International Conference on Power Electronics and Variable-Speed Drives.IET, London, 1994:458-464.

[4] JOO H G,KIM C G,SHIN H B,et al.Detection of three phase currents in space-vector PWM inverters with only one DC link current sensor[C]//International Conference on Industrial Electronics. Control, and instrumentation,IEEE,Taipei, 1996:127-132.

[5] METIDJI B,TAIB N,BAGHLI L.Phase current reconstruction using a single current sensor of three-phase AC motors fed by SVM-controlled direct matrix converters[J].IEEE Transactions Industrial Electronics,2013,60(12)5497-5505,.

[6] WANG C M,LIN S K.A simple single shunt current reconstruction approach for low-cost permanent magnet synchronous motor drives[C]//Proceedings of 2015 International Automatic Control Conference (CACS).IEEE, 2015:79-84.

[7] YANG J.Sliding-mode control for systems with mismatched uncertainties via a visturbance observer [J].IEEE Transactions on Industrial Electronics 2013, 60(1): 4398-4407.

[8] YANG J, LIU H, LI S et al.Nonlinear disturbance observer based robust tracking control for a PMSM drive subject to mismatched uncertainties[C]//Control Conference.IEEE,2012:830-835.

[9] 肖海峰，刘海龙，贺昱曜. PMSM的线性-滑模变结构直接转矩控制研究[J].电气传动，2014(5):35-39.

[10] HAN Y,LI P,ZHENG Z Q.Sliding-mode and back-stepping control for output tracking systems with unmatched uncertainties via a disturbance observer[C]//International Workshop on Variable Structure Systems.VSS,Nanjing,2016:308-311.

[11] 佘致廷,董旺华.基于反步滑模变结构的PMSM速度控制[J].控制工程，2016,23(S0):2-5.

[12] 韩京清.自抗扰控制器及其应用[J].控制与决策，1998,13(1):19-23.

[13] 夏长亮,刘均华.基于扩张状态观测器的永磁无刷直流电机滑模变结构控制[J].中国电机工程学报,2006,26(20):139-143.

[14] 陈强,南余荣,邢科新.基于扩张状态观测器的永磁同步电机混沌系统自适应滑模控制[J].物理学报,2014,63(22):113-120.