一种基于压电叠堆的微型直线超声波电动机研究

汪红兵，李志荣,2，孙春华

(1.苏州市职业大学,苏州 215104；2.呼和浩特职业学院，呼和浩特 010051)

0 引 言

随着工业和民用产品向高精密方向发展，在精密加工、精密测试等领域，迫切需要能够直接驱动且外形较小的直线超声波电动机。传统的磁性直线电动机有着悠久的发展历史，但由于原理限制，很难进一步缩小体积。而直线超声波电动机的工作原理区别于传统的电磁电机，是利用压电材料的逆压电效应，在弹性体中产生微观变形，并通过摩擦或其它作用方式将这种微观变形转换成宏观运动。直线超声波电动机具有体积小、质量轻、结构简单紧凑、低速大转矩、响应快、运动精度高、低噪声运行、无电磁干扰、可直接实现直线驱动、结构形式灵活多样等一系列优点，因此发展迅速，应用前景广阔[1-3]。

近三十年来，微型直线超声波电动机得到了迅速发展。日本学者在1989年制作了一种直梁式微型直线超声波电动机，电机的最大推力达到0.4 N[4]。日本公司在1998年推出了一种薄型直线超声波电动机，电机的最大推力可达到3 N[5]。2002年韩国学者开发的平板型直线超声波电动机推力可达到1.5 N[6]。上海大学李朝东等开发的卧式板型直线超声波电动机输出推力可达50 mN[7]。

笔者前期开发的一种直线超声波电动机采用了2个兰杰文振子的结构形式[8]，压电陶瓷采用多片形式，电机的外形尺寸较大，驱动电压较高，不适应一些精密工程领域的直线驱动需要[9]。为此本文利用压电叠堆的优良性能，在此基础上研究了一种基于压电叠堆的微型直线电动机，对其结构进行简化，使其具有驱动电压低、推重比大、结构简单、装配容易等特点。

1 初始直线超声波电动机

初始设计的直线超声波电动机定子如图1所示，主要部分包括驱动头、支座、尾部、压电片和螺栓。外形尺寸为118 mm×78 mm×21 mm(长×宽×厚)，单片压电片的尺寸为20 mm×5 mm×1 mm(外径×内径×厚)，共4片,性能测试表明该电机的无负载速可达到100.5 mm/s，最大推力可达到38.8 N，电机定子推重比为97 N/kg。因此，电机呈低速、大推力的特性。但该电机外形尺寸较大，不适用于精密加工、精密测试以及精密定位等精密工程领域。因此，本文对该电机进行了改进研究，使得外形尺寸更小、运行速度更高、堵推力更大。

图1 初始V形直线超声波电动机

2 基于叠堆微型直线超声波电动机

初始直线超声波电动机定子包括2个兰杰文振子，振子采用螺栓连接，电机定子通过支座固定，在设计时使得电机定子中的支座和压电片位于兰杰文振子的一阶纵振模态的节面处，定子包括驱动头和自由端的尾部，该结构形式使得电机外形尺寸较大。为减小电机体积，重新设计的电机的主要组成部分包括驱动头、支座及压电叠堆。压电叠堆是由自主设计的。驱动头和压电叠堆组成了电机的定子。定子的外形尺寸约为30 mm×17 mm×7 mm 。采用压电叠堆后的电机，定子结构上采用一端固支的形式，定子没有自由端的尾部，驱动头的2个端面和压电叠堆连接后直接固定在底座上，改进后的电机定子如图2所示。

图2 基于压电叠堆的直线超声波电动机定子

3 压电叠堆性能

压电叠堆具有输出力大、输出位移大、功耗低、效率高、体积小等优点，实现低电压驱动，可应用于包括超声波电动机在内的各种驱动场合。

图3给出了所研制的0.5% Co掺杂Pb0.98Bi0.02Zr0.51Ti0.48Zn0.010 3压电陶瓷不同烧结温度压电性能。该压电陶瓷在温度950 °C下烧结5 h，其性能参数为:相对介电常数1 190，压电常数270 pC/N，机电耦合系数分别为0.54(Kp)，0.46(Kt), 居里温度为346 °C，介电损耗角正切为0.6 %。与商用PZT-8压电陶瓷的水平相当。

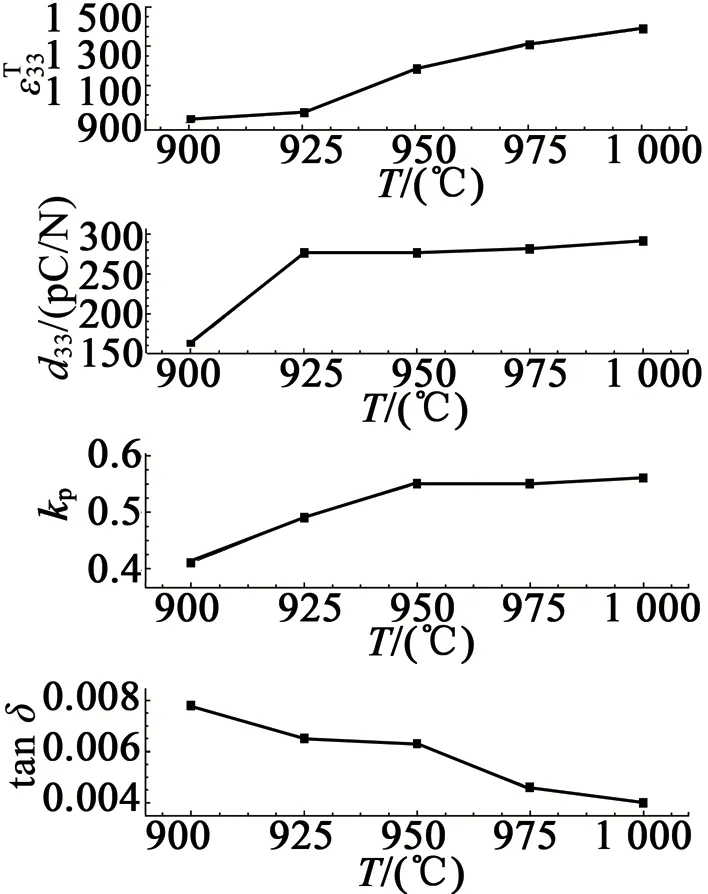
图3 所研制压电陶瓷不同烧结温度压电性能

对于所研制的压电陶瓷，委托相关公司采用流延多层叠烧技术进行了压电叠堆加工。

4 微型电机的原理及设计

4.1 电机原理

电机定子的2个端面固定约束，采用的工作模态是横向的反对称振动模态和纵向的对称振动模态，驱动头所连接的2个压电叠堆在一个伸长及另一个收缩时驱动产生横向反对称振动，此为横向反对称振动模态，如图4所示。当驱动头所连接的2个压电叠堆同时伸长或收缩时产生纵向对称振动，此为纵向对称振动模态，如图5所示。当加在左右2个压电叠堆上的激振电压同频但相位差为90°时，定子的驱动头由纵向和横向振动相叠加构成了椭圆运动。

图4 定子横向反对称振动模态

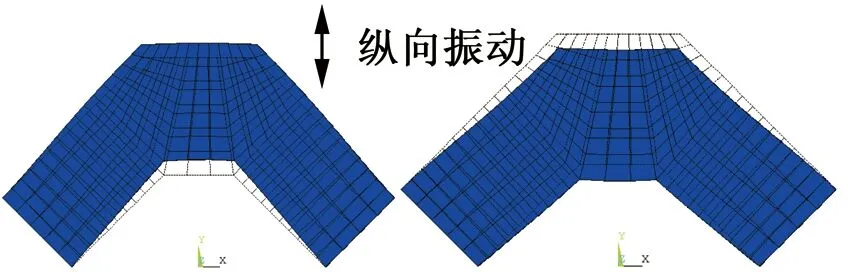
图5 定子纵向对称振动模态

电机是基于横向的反对称振动模态和纵向的对称振动模态工作的，只有2个模态频率尽可能保持一致，电机才能有效工作。下面对2个模态频率灵敏度进行分析，为电机定子设计提供参考依据。

4.2 模态频率灵敏度分析

电机定子的基本结构及参数如图6所示。

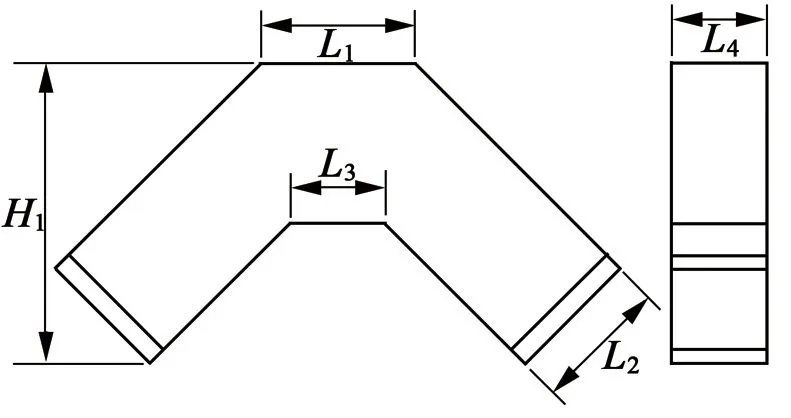
图6 定子结构图

在ANSYS中创建电机定子的有限元模型，定子上金属体部分采用solid45单元，该单元是三维8节点6面体，压电陶瓷采用solid5单元，该单元是三维8节点6面体压电耦合单元。定子弹性体选用材料为黄铜，其密度为8 270 kg/m3，弹性模量为920 GPa，泊松比为0.33。支座采用45号钢。压电陶瓷选用自主研发。定子的2个端面进行固定约束。建立的有限元模型如图7所示。

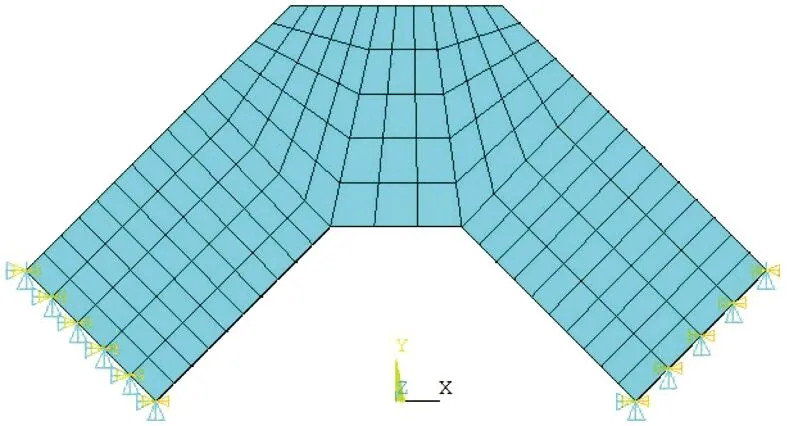
图7 ANSYS中定子的有限元模型

在ANSYS软件中使用模态分析功能可得到定子横向的反对称振动模态频率和纵向的对称振动模态频率对结构参数的灵敏度。

下面是使用有限元方法求解定子2个模态频率对结构参数灵敏度的过程。

设定子的第i阶频率是ωi，定子第j个结构参数是tj，定子的第i阶频率相对于第j个参数的灵敏度：

通过有限元方法分析可得：

定子结构参数L1对横向和纵向模态频率的影响如图8所示。

图8 定子参数L1对横向和纵向模态频率影响

定子结构参数L2对横向和纵向模态频率的影响如图9所示。

图9 定子参数L2对横向和纵向模态频率影响

定子结构参数L3对横向和纵向模态频率的影响如图10所示。

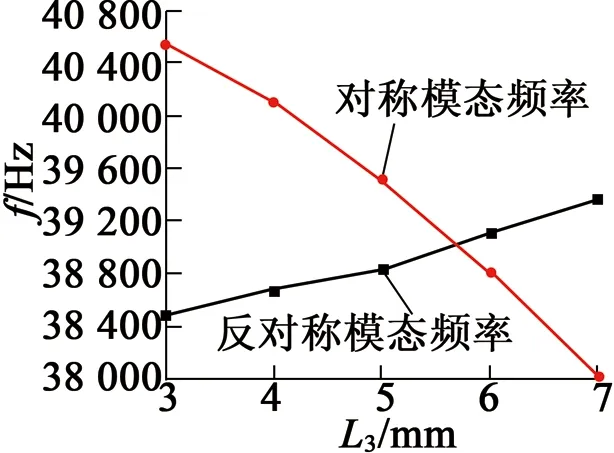
图10 定子参数L3对横向和纵向模态频率影响

定子结构参数L4对横向和纵向模态频率的影响如图11所示。

图11 定子参数L4对横向和纵向模态频率影响

定子结构参数H1对横向和纵向模态频率的影响如图12所示。

图12 定子参数H1对横向和纵向模态频率影响

根据定子横向和纵向模态频率对各结构参数的影响变化情况，得出定子横向和纵向模态频率对结构参数的灵敏度。图13为横向模态频率对结构参数灵敏度，从图13可以看出定子结构参数L1，L2以及H1对反对称模态频率影响较大。图14为纵向模态频率对结构参数灵敏度，从图14可以看出定子结构参数L1，L2以及H1对对称模态频率影响较大。

图13 横向模态频率

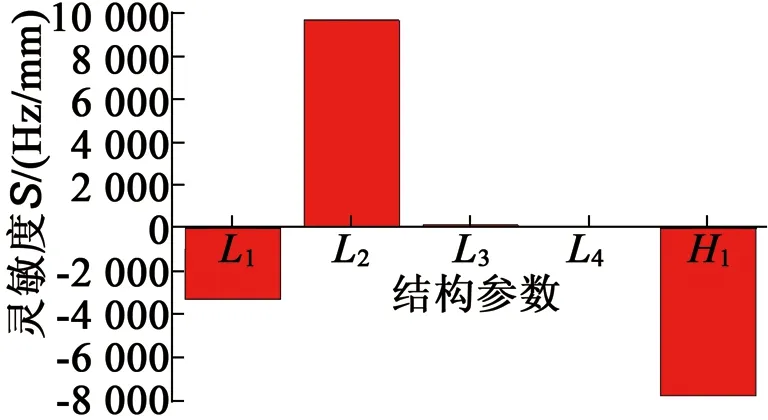
图14 纵向模态频率

通过对定子各结构参数对横向和纵向态频率的灵敏度分析，调整各结构参数，确定出定子横向模态频率为39 571 Hz，纵向模态频率为38 837 Hz，两者频率基本一致。

5 微型电机制作与实验

整机如图15所示，定子的外形尺寸为30 mm×17 mm×7 mm，远小于初始电机外形尺寸。

图15 样机的整机图

电机主要包括定子、动子和若干附属部分，其附属部分起到装夹和调整预紧力作用。

下面对电机定子进行模态测试，测试所用的仪器是PSV-300F型激光多普勒测振仪。将反相电压信号同时连接在电机定子的左右2个压电叠堆上，所测得的定子频率响应曲线如图16所示，图16中纵坐标是定子驱动头切向速度振幅。定子左右2个压电叠堆同时接入同相电压信号，激光测振仪测试得到定子频率响应曲线如图17所示，图17中纵坐标是定子驱动头法向速度振幅。由图16、图17可知，纵向模态为38 100 Hz，横向模态为37 850 Hz，理论计算和实测数值基本一致。

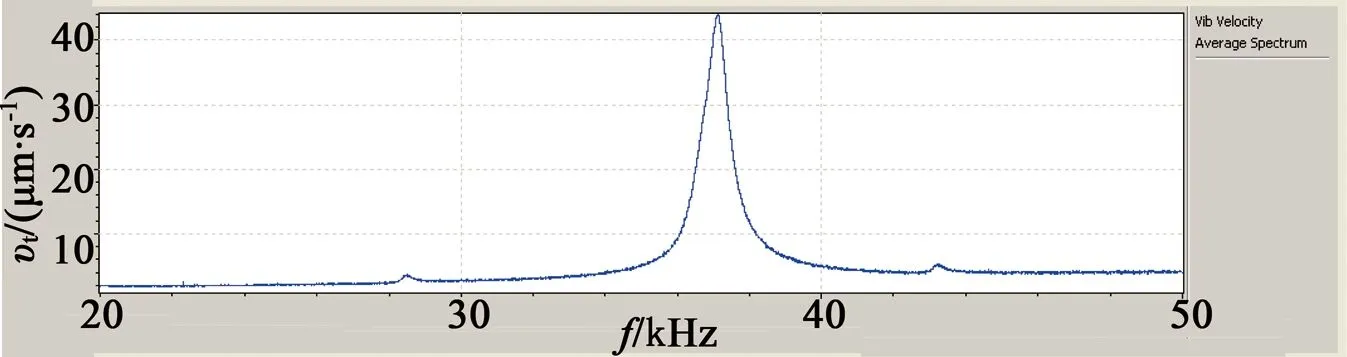
图16 定子驱动头切向扫频图

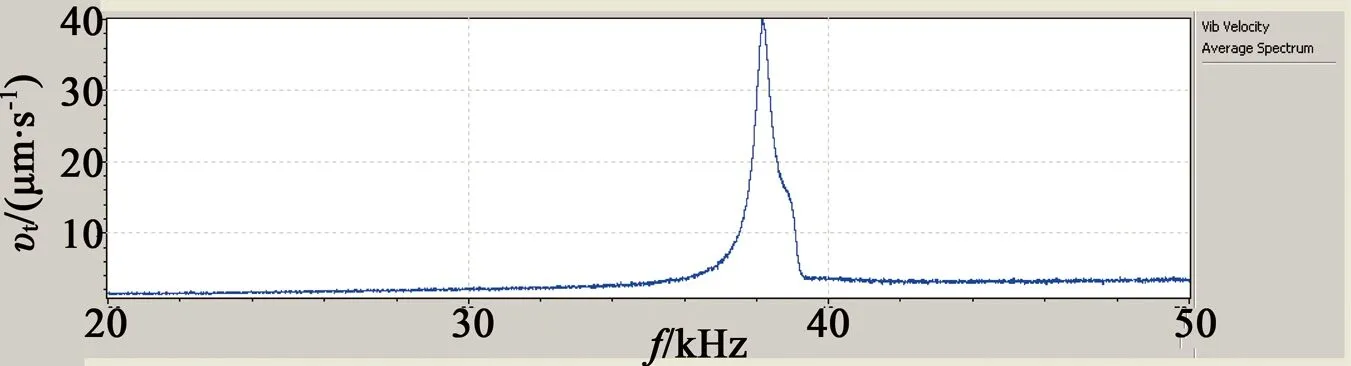
图17 定子驱动头法向扫频图

对电机的输出性能进行了测试。当激励电压为15 V、频率为38 000 Hz时，样机的无负载最大速度为30 mm/s，以及最大推力为2.2 N。电机定子推重比为157 N/kg，微型化后电机推重比增加1.7倍。

6 结 语

为解决双兰杰文振子的V形直线超声波电动机外形尺寸较大的问题，更好地应用于精密工程领域，对V形直线超声波电动机进行了微型化改进设计。电机采用压电叠堆并对结构进行重新设计，使得初始电机尺寸从118 mm×78 mm×21 mm(长×宽×厚)降到30 mm×17 mm×7 mm，可有效适应一些精密工程领域的应用。

电机采用自主设计的压电叠堆，与商用PZT-8压电陶瓷的水平相当，满足电机的性能要求。

电机定子使用对称和反对称模态作为工作模态，当2种模态频率一致时电机才具有最佳性能。使用有限元方法分析了电机定子的对称和反对称模态频率对结构参数的灵敏度，找出灵敏度较高的结构参数，并对其进行调整，使得定子的对称和反对称模态频率保持一致。对所设计的电机定子进行了模态测试，实验结果与理论分析基本一致。

对所设计的电机进行了性能测试，当激励电压为15 V、频率为38 000 Hz时，样机的无负载最大速度为30 mm/s，最大推力为2.2 N。微型化后的电机定子推重比为157 N/kg，微型化前的电机定子推重比为97 N/kg，微型化后电机推重比增加1.7倍。

[1] 赵淳生.超声电机技术与应用[M].北京:科学出版社, 2007.

[2] 赵淳生.面向21 世纪超声电机技术的研究[J].中国工程科学, 2002, 14(2):86-91.

[3] 胡敏强,金龙,顾菊平.超声波电机原理与设计[M].北京:科学出版社,2005.

[4] 上羽贞行，富川义郎.超声波马达理论与应用[M].杨志刚，郑学伦，译.上海：上海科学技术出版社,1998.

[5] TAKANO T,TOMIKAWA Y.Characteristics of the ultrasonic linear motor radial and nonaxisymmetric vibration modes of an annular plate[J].Japanese Journal of Applied Physics,1995(41):5288-5291.

[6] PARK T,KIM B,KIM M H et al.Characteristics of the first longitudinal-fourth bending mode linear ultrasonic motors[J].Japanese Journal of Applied Physics,2002(41):7139-7143.

[7] 李朝东，何晓箐.卧式板型直线超声电机的微型化[J].光学精密工程，2010，18(4):887-892.

[8] 汪红兵，李志荣，孙春华.V形大推力直线超声电机定子振动的有限元分析[J].微特电机，2013，41(8):40-42.

[9] ASUMI K, FUKUNAGA R, FUJIMURA T,et al..Miniaturization of a V-shape Transducer ultrasonic Motor[J],Japanese Journal of Applied Physics,2009(48):07GM02.