SRM状态转换表和应用中新状态获取方法

王吉华，任传波，曲金玉，李 超

(山东理工大学, 淄博 255000)

0 引 言

随着开关磁阻电机(以下简称SRM)在航空航天、矿山、纺织、家电和交通等领域的广泛应用，人们对其调速系统的研究越来越重视。SRM的运行控制要遵循 “磁阻最小”原理，即在转子合适位置给对应的定子相绕组通电和断电进行换相控制，确保合适的开通角和关断角，达到正常运行和进一步调节转速、转矩等目的[1，2]，可见，转子位置检测是驱动控制的关键环节之一。

转子位置检测有直接和间接法。前者是利用光电和磁敏等位置传感器进行检测，后者是无位置传感器检测，利用测得的相电压[3]和相电流[4-6]等估算磁链和电感等电磁量，也有直接测得附加线圈电感[7，8]和附加电容值[9]等，再分别由磁链、电流、电压、电感和电容等与转子位置的关系来获取转子位置参数。由于传感器检测的成本、体积和可靠性等因素，无传感器的间接检测方法一直是近年来研究热点，并取得了很多重要成果，但目前还没有达到普及应用[10，11]。

目前在市场上应用多的仍然是传感器直接检测[12-16]，特别是在大中型SRM调速系统中，而且传感器直接检测可作为航空航天等重要领域SRM位置检测的冗余备份[10]。对于SRM调速系统，只要能检测到转子的关键位置信息即可进行换相控制，传感器直接位置检测和部分无传感器位置检测[17，18]均基于这种思想。换相控制需检测出这些关键位置，并且当转子从一个关键位置到另一个关键位置转换时传感器输出值必须作出相应变化，此值称作转子的一个位置状态，一个电角度周期内若干个状态就组成状态转换表。它是换相控制的重要依据，但文献中很少有对其进行具体的分析，特别是在设计实践中的新状态值获取方法。

因此，以目前应用中占大多数的光电位置传感器为例，针对转子相对位置和传感器输出值分析状态转换表及其规律；分析在电机运行时直接读取传感器来获取新状态值所遇到的问题，基于状态转换表规律，提出了依据上一次状态值和捕捉当前输出值发生变化的传感器编号而通过查表获取的方法，并设计转子正反转查询的表格。状态转换表分析和实践中获取新状态值的思路和方法对于其它结构形式的SRM调速系统均适用，可提供参考和借鉴。

1 位置分布关系

分析状态转换表可从转子、定子和位置传感器的相对位置关系着手。针对某三相12/8 SRM，对其进行拆卸和位置关系测量，如图1所示，确定其光电位置传感器(实质为光耦，后简称光耦)、定子和转子的分布及位置关系，如图2所示。在图2中，3个光耦按圆周方向固定安装在电机后端盖上，其和定子均用粗实线表示，二者刚性连接；挡板和挡板间隙交叉分布在挡板圆盘的外圆周上，挡板圆盘和转子均刚性连接在转子轴上，挡板圆盘和转子用细实线表示；定子、转子、光耦安装圆周面和挡板圆盘四者同轴。光耦槽正对于挡板所在的挡板盘外圆周，当挡板盘随着转子一起转动时，挡板和挡板间隙将轮流通过3个光耦槽。

图1 SRM拆卸图

图2 SRM位置关系图

图2中，将转子和定子圆周平分为48个扇形，用虚线标识，每个虚线夹角即机械角为7.5°，由于对称性和为了简化，只标出相对的2个90°区域。定子上A，B和C三相各有4个凸极1～4，转子有凸极1～8。定子是凸极和凹槽均为15°的均匀交叉分布，3个光耦是两两中心线之间为15°的均匀分布，见图2中的双点划线，并且中间光耦的中心线和定子凸极B1中心线重合。转子是凸极15°和凹槽30°的交叉分布，挡板盘的外圆周上是挡板和挡板间隙均为22.5°的均匀交叉分布，并且挡板顺时针转动的前边沿和各个转子凸极中心线重合。电机运行时，刚性连接的定子和光耦静止，而刚性连接的转子和挡板盘同轴转动。

当一款SRM定型生产时，其定子、转子、光耦位置传感器和挡板圆盘四者的装配关系将确定，这决定了在转子转动一周的各个位置上这四者的相对位置虽各不相同但均确定，图2为某一位置上这四者的相对位置关系。由于转子和挡板盘刚性同轴连接，挡板和转子凸极的相对位置固定；定子和光耦位置传感器刚性连接，定子凸极和传感器的相对位置固定。当转子转动时，挡板和挡板间隙轮流通过光耦槽，光耦将产生的变化输出，不同的输出就代表了转子凸极和定子凸极离散的关键相对位置信息，即状态，状态变化的时刻就是关键位置检测点。

2 关键位置检测点

根据SRM的电感线性模型[1-2]和图2的电机结构特点，分析转子关键位置检测点。电机为12/8三相结构，每相四极串联，由SRM设计理论可知，转子极距τr=45°，步进角θstep=15°，在图2的电机结构中，由于3个光耦两两夹角15°，挡板和挡板间隙为22.5°均匀分布，使得转子每转动7.5°就有一个光耦的值发生变化，可检测半个步距的相对位置关系，控制可更加精细。

由于转子转动一个转子极距就完成了一个电角度周期，由图2可看出，3个光耦相邻极A1，B1和C1的各自相邻转子极8-1，1-2和2-3均分别完成一个电角度周期，而A，B，C三相的各自4个极1～4与各自的相邻转子极位置关系完全相同，所以只需选择某相一个极与转子一个极来分析关键位置检测。以B1和转子极1为例，并假设B1为通电相，随转子转动的电感变化和对应角度如图3所示。

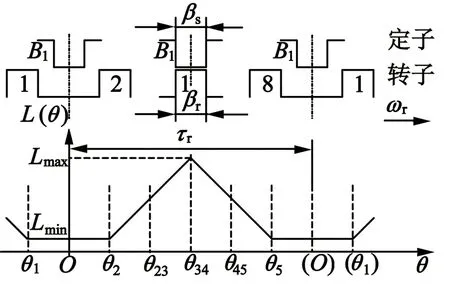
图3 关键位置检测点分布图

图3中， 对应图2的顺时针旋转方向，每2条虚线之间夹角对应机械角为7.5°和电角度60°，从O到(O)的转子极距τr对应机械角为45°和电角度360°，转子每顺时针转动7.5°就对应一个关键位置检测点，如图3中各条虚线对应的θ轴上点和角度。由图2结构图，在θ轴上，从O向顺时针转动方向的θ5各检测点，依次对应转子凸极1和2的凹槽中心与A1和B1的凹槽中心对齐、转子凸极1前边沿与B1后边沿对齐、转子凸极1前边沿与B1中心对齐、转子凸极1前边沿与B1前边沿对齐(即两者的中心对齐)、转子凸极1中心与B1前边沿对齐、转子凸极1后边沿与B1前边沿对齐等6个关键位置检测点。

O对应图2位置状态下转子极1的相对位置角0。B1绕组电感为最小值Lmin，O和θ2之间通常为开通角区域；θ2到θ34之间为电感上升区域；由于定子极弧βs和转子极弧βr相等，且均为15°，最大电感Lmax退化为一个点，对应角度范围为0；θ23和θ34之间通常为关断角区域；θ34到θ5之间是电感下降区域。

这样就可根据各区域控制的需要，由该区域的前后检测点为基准进行相应的转速和角度计算，从而达到换相控制所需的准确时刻。当到达一个检测点时，将有1个光耦输出值发生变化，3个光耦组合值也就发生变化，即状态值变化，实际应用中转子相对位置就是通过变化的状态值来得到。

3 状态转换分析和状态转换表规律

在转子和挡板盘转动时，分析转子相对位置的变化，并通过挡板盘和3个光耦组成的检测电路所输出的值表示这些位置状态转换关系，从而得到状态转换表，并分析其规律。

3个光耦的检测电路相同，以1号光耦为例，如图4所示。当挡板挡住时，光敏三极管不接收光而断开，P1输出低电平，逻辑值为0；当间隙通过光耦时，光敏三极管接收光而导通，P1输出高电平，逻辑值为1。光耦1、2和3的输出结果依次从低位到高位排列，形成一个三位二进制数作为状态值，此状态值就表示了挡板圆盘的位置即转子的相对位置。

图4 光耦检测电路

为了便于分析，将图2中定子和转子圆柱体沿同一棱剖开，将圆周方向位置分布展成直线方向位置分布，如图5和图6所示，分别表示转子顺、逆时针方向转动，并假设单相通电使转子转动。分析时，不妨将图2中的位置作为进入各自状态1的临界位置，转子顺时针转动一个角度即进入顺时针状态1，如图5；转子逆时针转动一个小角度即进入逆时针状态1，如图6。每两条虚线间隔为机械角7.5°，转子和挡板圆盘每转动7.5°状态值将发生一次变换。由图3可知，一个电周期由6个状态组成，每一相定子极的相对位置均按此作周期性变化。

对于顺时针转动的状态1，如图5，光耦3被挡板挡住而输出0，光耦1和光耦2通过间隙而输出1，对应状态值为二进制数011B(十进制数3)，应使C相通电而到达下一个状态。同理，状态2～6的状态值分别为010B(2)，110B(6)，100B(4)，101B(5)和001B(1)，并应分别使B，B，A，A和C相通电而到达各自的下一个状态。

同样，对于转子逆时针转动的状态1，如图6，光耦2和光耦3被挡板挡住而输出0，光耦1通过间隙而输出1，对应状态值为001B(1)，应使A相通电而到达下一个状态。同理，状态2～6的状态值分别为101B(5)，100B(4)，110B(6)，010B(2)和011B(3)，并应分别使B，B，C，C和A相通电而到达各自的下一个状态。

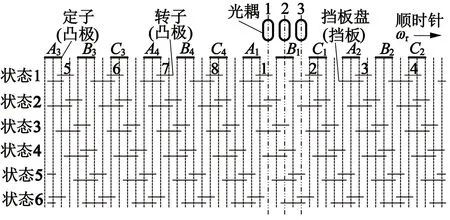
图5 转子顺时针转动时位置状态分析图

图6 转子逆时针转动时位置状态分析图

总结以上分析，便可得到转子顺、逆时针转动的位置状态转换表，如表1所示，其均以图2中的临界位置为起始点。对于状态转换表，状态1～6仅是为了便于分析而进行的人为定义，对实际控制系统并无作用，实际起作用的是单片机读取光耦检测的状态值，是换相控制的依据。各状态值下的单相通电仅是为了分析需要而采用的一种换相控制方式，实际中不同的控制目的和策略可对应不同的方式。

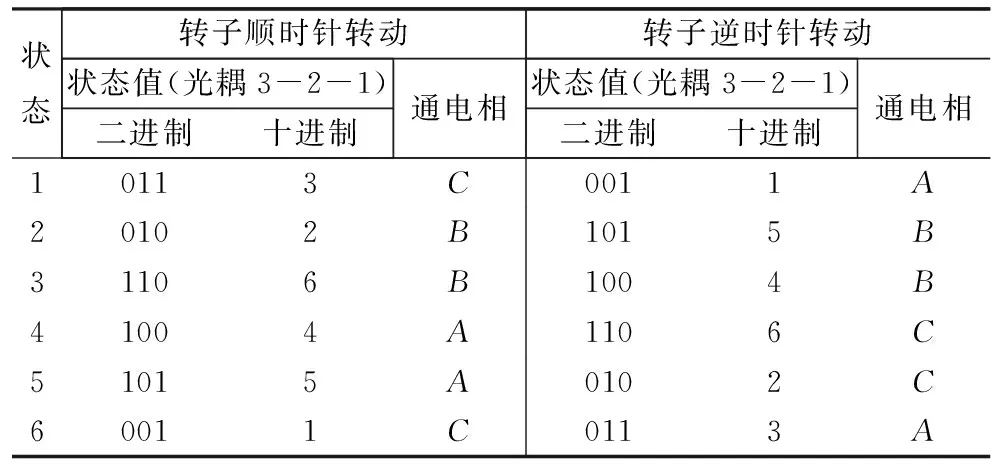
表1 三相12/8 SRM的状态转换表

从表1可以得到如下规律：

(1)总体看，在一个转子极距内，转子顺、逆时针转动的状态值转换顺序和通电相刚好相反。顺时针状态是3-2-6-4-5-1-3周期循环，通电是C-B-A-C相循环；相反，逆时针分别是1-5-4-6-2-3-1和A-B-C-A循环。

(2)在一个转子极距内，针对同一状态值，也即转子的同一位置区域，顺、逆时针方向转动的下一个状态值不同。

(3)在一个转子极距内，针对同一状态值，顺、逆时针方向转动的通电相不同。

(4)从二进制数可看出，顺、逆时针方向转动的相邻状态值变换均由其中一个相应的传感器值变化引起。

(5)从二进制数可看出，顺、逆时针方向转动上，引起相邻状态值变化的光耦是相邻的，其沿着各自转动方向，而且是3个光耦作周期性循环变化。

(6)从二进制数可看出，引起相邻状态值变化的相邻光耦的输出值是逻辑值0和1交错循环的，即沿旋转方向某挡板前边沿或某挡板后边沿正对光耦中心线，挡板进入或退出光耦检测区。

(7)从图2～图6可知，某光耦值发生变化的时刻，即状态值发生变化的时刻，正是关键位置检测点，即转子进入下一位置状态的起始点。

规律(1)和(2)仅从总体上反映了顺、逆时针方向上变化趋势的差异，(3)是二者“磁阻最小”原理的本质上区别，(4)～(7)是转子相对位置关系在外在表现上的不同。总之，状态转换表不能将顺、逆时针方向状态值和通电相按相反顺序排列来简单地表示，而完整的状态转换表应包含十进制数状态值、通电相和反映光耦值变化规律的二进制数状态值，而且要有三者之间的一一对应关系。

4 获取当前状态值的方法

对于一款SRM，其结构和状态转换表确定，是单片机调速控制的重要依据，关键是单片机要获得电机运行的当前时刻状态值和关键检测点的准确时刻，才能根据状态表准确地进行换相控制。从图5和图6的分析可看出，表1中状态值是通过单片机读取3个光耦值而得到，但此方法在各种转速下并不是都可以得到准确的换相时刻。

单片机汇编语言或C语言的主程序均采用顺序结构，含有跳转和中断响应。读取光耦语句将放在主程序大循环中或某个中断响应中；前者需等到下一循环到来时才能读取，后者需等到此中断事件发生时才能读取；两者均需等待一定时间，前者时间不确定，后者时间可能确定，如定时中断，但电机转速却不确定。这将带来2个问题：一是状态漏检，特别是高速运行时；二是读取状态不一定是在刚进入此状态的时刻，即关键位置检测点。

解决方法是利用单片机捕捉功能，由表1规律(4)、 (5)和 (7)，实时捕捉状态变化的准确时刻。又由规律(6)，光耦输出变化可能是上升沿或下降沿，则捕捉模块要设置为上升沿和下降沿均捕捉，由此不会发生状态漏检，克服了以上2个问题。

但会带来另一问题，捕捉并不像读取那样能得到当前状态值。若采用捕捉并读取的方法，也只能在捕捉中断响应中读取，但从捕捉事件发生到进入捕捉中断响应来读取需要一个时间片，这将影响换相控制的滞后，特别在高速时可能会造成控制失败。

单片机查表能有效提高实时性，为此，通过捕捉和查表的方式来获取当前状态值。由状态表规律(4)～(6)，对于转子顺、逆时针方向转动，状态值和光耦变化规律存在一一对应关系，将上一个状态值作为行，当前发生跳变的光耦编号作为列，设计的二维表格如表2所示，“*”表示不会被查表而可设置为单片机寄存器任何值。某种意义上，表2是用于捕捉的状态转换表，和表1一一对应。此表格也包含了表1的正反转，查询时不必考虑正反转。

表2 单片机新状态查询二维表

由于捕捉必须发生在转子转动时，在静止起动时刻仍然采用读取3个光耦值获取状态，此时不存在实时性问题，硬件上与3个捕捉端口线并联3个普通I/O口线来实现。静止起动时读取状态值也是必需的，为查表提供初始的上一次状态值。以上分析的状态转换表和状态值获取方法，已经在某12/8 SRM调速系统上进行了应用，经起动及各种转速下的实验，均能可靠运行。

5 结 语

从SRM的工程应用角度，测得位置传感器、定子和转子的位置关系，分析关键位置检测点、状态转换表及其规律；分析电机运行时采用读取光耦方法获得新状态值可能带来的问题，利用状态转换表规律，提出利用捕捉和查表获取的方法，并设计包含了正反转的二维查询表格。状态转换表分析方法和新状态值获取方法已在调速系统中得到验证，可为SRM的工程应用提供参考。

[1] 王宏华.开关磁阻电动机调速控制技术[M].北京:机械工业出版社,2014.

[2] 吴红星.开关磁阻电机系统理论与控制技术[M].北京:中国电力出版社,2010.

[3] 李广海,叶勇,蒋静坪.开关磁阻电机无位置传感器技术的分析[J].微特电机,2004,32(7):5-7，44.

[4] 张旭隆,谭国俊,蒯松岩,等.在线建模的开关磁阻电机四象限运行无位置传感器控制[J].电工技术学报,2012,27(7):26-33.

[5] 蔡骏,邓智泉.基于相电感综合矢量法的开关磁阻电机初始位置估计[J].中国电机工程学报,2013,33(12):145-151,197.

[6] 罗德荣,李亚雄,蔡亚辉,等.基于电感极值的开关磁阻电机无位置传感技术[J].电力电子技术,2016,50(4):63-66.

[7] 毛良明,经亚枝,樊小明,等. 反串线圈法间接位置检测技术在开关磁阻发电机系统中的应用研究[J].中国电机工程学报,2000,20(10):27-30.

[8] 李根,徐建单,程昭竣,等.基于外加线圈的开关磁阻电机无位置传感技术[J].微特电机,2016,44(6):51-54.

[9] 詹琼华,王双红,肖楚成.开关磁阻电动机电容式位置检测技术[J].电工技术学报,1999,14(3):2-6.

[10] 邓智泉,蔡骏.开关磁阻电机无位置传感器技术的研究现状和发展趋势[J].南京航空航天大学学报,2012,44(5):611-620.

[11] 王骋,邓智泉,蔡骏,等.电机转子位置传感器的评述与发展趋势[J].微特电机,2014,42(3):64-71.

[12] 张超,全力,朱孝勇,等.基于DSP+CPLD的车用开关磁阻电机驱动控制系统的设计[J].电机与控制应用,2013,40(1):13-16,21.

[13] 姬起群,施火泉.基于C8051F500的开关磁阻电动机控制系统设计[J].微特电机,2013,41(2):60-62.

[14] 魏宏财.基于DSP的矿用运输机车调速系统设计[J].煤炭技术,2017,36(9):204-206.

[15] 蔡燕,尹磊,姜文涛.开关磁阻电机调速系统半实物仿真平台设计[J].微特电机,2017,45(7):41-44.

[16] CHEN H,GU J J.Implementation of three-phase switched reluctance machine system for motors and generator[J].IEEE ASME Transactions on Mechatronics,2010,15(3):421-432.

[17] 邱亦慧,詹琼华,马志源,等.基于简化磁链法的开关磁阻电机间接位置检测[J].中国电机工程学报,2001(10):60-63,121.

[18] 陈坤华,孙玉坤,吴建兵,等.基于电感模型的开关磁阻电机无位置传感技术[J].电工技术学报,2006,21(11):71-75.